当前位置： 首页 > news >正文

YOLOv8 windows下的离线安装 offline install 指南 -- 以 带有CUDA版本的pytorch 为例

news 2025/12/17 7:03:33

文章大纲

  • 简介
  • 基础环境与安装包的准备
    • windows 下 lap 包的离线安装
    • conda 打包基础环境
    • 使用 pip 下载 whl 包
    • 特别的注意：pytorch cuda 版本的下载
  • 迁移与部署流程
    • 基础python 的conda 环境迁移与准备
    • 必备包： 安装cuda 版本 的torch，torchvision，ultralytics
  • 参考文献与学习路径

简介

前置文章：

  • YOLOv8 多目标跟踪与常见问题汇总

基础环境与安装包的准备

为什么不直接使用conda-pack 迁移环境呢，因为带cuda 的pytorch 包过大，大概5G 左右，可能在copy 中出现错误。

    <

相关文章：

YOLOv8 windows下的离线安装 offline install 指南 -- 以 带有CUDA版本的pytorch 为例

文章大纲 简介基础环境与安装包的准备windows 下 lap 包的离线安装conda 打包基础环境使用 pip 下载 whl 包特别的注意：pytorch cuda 版本的下载迁移与部署流程基础python 的conda 环境迁移与准备必备包： 安装cuda 版本 的torch，torchvision，ultralytics参考文献与学习路径…...

编程日记 2023/10/16 3:29:22

百度车牌识别AI Linux使用方法-armV7交叉编译

1、获取百度ai的sdk 百度智能云-登录 (baidu.com) 里面有两个版本的armV7和armV8架构。v7架构的性能比较低往往需要交叉编译&#xff0c;v8的板子性能往往比较好&#xff0c;可以直接在板子上编译。 解压到ubuntu里面。这里介绍v7架构的。 2、ubuntu环境配置 ubuntu下安装软件…...

编程日记 2023/10/16 3:26:17

数学建模——确定性时间序列分析方法

目录 介绍 确定性时间序列分析方法 1、时间序列的常见趋势 &#xff08;1&#xff09;长期趋势 &#xff08;2&#xff09;季节变动 &#xff08;3&#xff09;循环变动 &#xff08;4&#xff09;不规则变动 常见的时间序列模型有以下几类 2、时间序列预测的具体方法 …...

编程日记 2023/10/16 3:24:14

Opencv——颜色模型+通道分离与合并

视频加载/摄像头调用 VideoCapture允许一开始定义一个空的对象 VideoCapture video VideoCapture(const String &filename,int apiPreferenceCAP_ANY) filename:读取的视频文件或者图像序列名称 apiPreference:读取数据时设置的属性&#xff0c;例如编码格式、是否调用Op…...

编程日记 2023/10/16 3:23:13

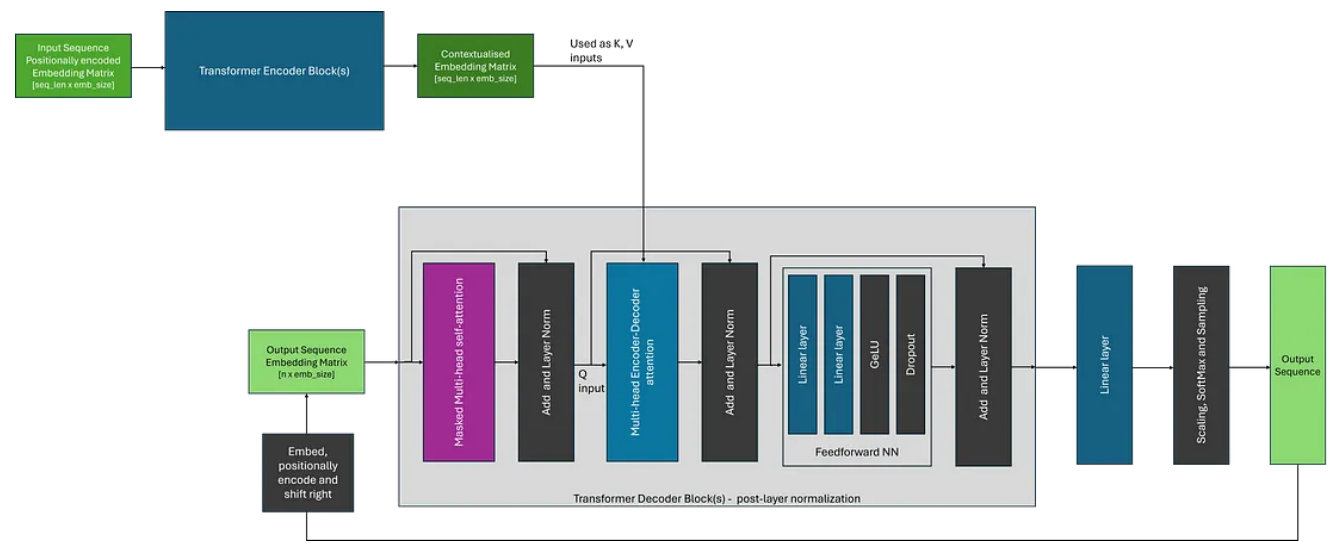
解码自然语言处理之 Transformers

自 2017 年推出以来&#xff0c;Transformer 已成为机器学习领域的一支重要力量&#xff0c;彻底改变了翻译和自动完成服务的功能。 最近&#xff0c;随着 OpenAI 的 ChatGPT、GPT-4 和 Meta 的 LLama 等大型语言模型的出现&#xff0c;Transformer 的受欢迎程度进一步飙升。这…...

编程日记 2023/10/16 3:22:12

【前端设计模式】之迭代器模式

迭代器模式是一种行为设计模式&#xff0c;它允许我们按照特定的方式遍历集合对象&#xff0c;而无需暴露其内部实现。在前端开发中&#xff0c;迭代器模式可以帮助我们更好地管理和操作数据集合。 迭代器模式特性 封装集合对象的内部结构&#xff0c;使其对外部透明。提供一…...

编程日记 2023/10/16 3:20:09

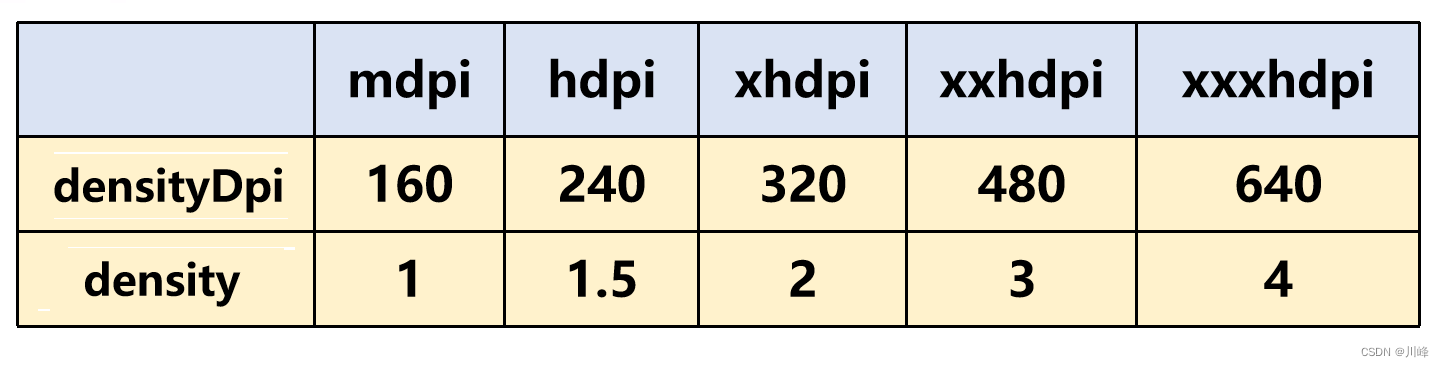
【Android知识笔记】图片专题（BitmapDrawable）

如何计算一张图片的占用内存大小？ 注意是占用内存，不是文件大小可以运行时获取重要的是能直接掌握计算方法基础知识 Android 屏幕像素密度分类： （其实还有一种 ldpi = 120，不过这个已经绝种了，所以最低的只需关心mdpi即可） 上表中的比例为：m : h : xh : xxh: xxxh = …...

编程日记 2023/10/16 3:18:05

前端工程化知识系列（10）

目录 91. 了解前端工程化中的容器化和云部署概念&#xff0c;以及如何使用Docker和Kubernetes等工具来实现它们&#xff1f;92. 你如何管理前端项目的文档和知识共享&#xff0c;以确保团队成员都能理解和使用前端工程化工具和流程&#xff1f;93. 了解前端开发中的大规模和跨团…...

编程日记 2023/10/16 3:16:04

大数据flink篇之三-flink运行环境安装（一）单机Standalone安装

一、安装包下载地址 https://archive.apache.org/dist/flink/flink-1.15.0/ 二、安装配置流程 前提基础&#xff1a;Centos环境&#xff08;建议7以上&#xff09; 安装命令&#xff1a; 解压&#xff1a;tar -zxvf flink-xxxx.tar.gz 修改配置conf/flink-conf.yaml&#xff1…...

编程日记 2023/10/16 3:12:59

Redisson使用延时队列

延时队列 在开发中&#xff0c;有时需要使用延时队列。 比如&#xff0c;订单15分钟内未支付自动取消。 jdk延时队列 如果使用 jdk自带的延时队列&#xff0c;那么服务器挂了或者重启时&#xff0c;延时队列里的数据就会失效&#xff0c;可用性比较差。 Redisson延时队列 …...

编程日记 2023/10/16 3:11:58

基于php 进行每半小时钉钉预警

前言 业务场景&#xff1a;监控当前业务当出现并发情况时技术人员可以可以及时处理 使用技术栈&#xff1a; laravelredis 半小时触发一次报警信息实现思路 1、xshell脚本 具体参数就不详细解释了&#xff0c;想要详细了解可以自行百度 curl -H "Content-Type:appl…...

编程日记 2023/10/16 3:08:55

5.Python-使用XMLHttpRequest对象来发送Ajax请求

题记 使用XMLHttpRequest对象来发送Ajax请求&#xff0c;以下是一个简单的实例和操作过程。 安装flask模块 pip install flask 安装mysql.connector模块 pip install mysql-connector-python 编写app.py文件 app.py文件如下&#xff1a; from flask import Flask, reque…...

编程日记 2023/10/16 3:06:53

八皇后问题的解析与实现

问题描述 八皇后问题是一个古老而又著名的问题。 时间退回到1848年，国际西洋棋棋手马克斯贝瑟尔提出了这样的一个问题： 在88格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问一共有多少种摆法。 如何找到这所有的…...

编程日记 2023/10/16 3:04:50

论文浅尝 | 深度神经网络的模型压缩

笔记整理&#xff1a;闵德海&#xff0c;东南大学硕士&#xff0c;研究方向为知识图谱 链接&#xff1a;https://arxiv.org/abs/1412.6550 动机 提高神经网络的深度通常可以提高网络性能&#xff0c;但它也使基于梯度的训练更加困难&#xff0c;因为更深的网络往往更加强的非线…...

编程日记 2023/10/16 3:03:49

进阶JAVA篇- DateTimeFormatter 类与 Period 类、Duration类的常用API（八）

目录 1.0 DateTimeFormatter 类的说明 1.1 如何创建格式化器的对象呢&#xff1f; 1.2 DateTimeFormatter 类中的 format&#xff08;LocalDateTime ldt&#xff09; 实例方法 2.0 Period 类的说明 2.1 Period 类中的 between(localDate1,localDate2) 静态方法来创建对象。 3.…...

编程日记 2023/10/16 3:02:47

1.1 Windows驱动开发：配置驱动开发环境

在进行驱动开发之前&#xff0c;您需要先安装适当的开发环境和工具。首先&#xff0c;您需要安装Windows驱动开发工具包&#xff08;WDK&#xff09;&#xff0c;这是一组驱动开发所需的工具、库、示例和文档。然后&#xff0c;您需要安装Visual Studio开发环境&#xff0c;以便…...

编程日记 2023/10/16 3:01:47

Jetpack：009-kotlin中的lambda、匿名函数和闭包

文章目录 1. 概念介绍2. 使用方法2.1 函数类型的变量2.2 高阶函数 3. 内容总结4.经验分享 我们在上一章回中介绍了Jetpack中Icon和Imamg相关的内容&#xff0c;本章回中主要介绍Kotlin中的 lambda、匿名函数和闭包。闲话休提&#xff0c;让我们一起Talk Android Jetpack吧&…...

编程日记 2023/10/16 3:00:46

openGauss指定schema下全部表结构备份与恢复

本次测试针对openGauss版本为2.0.5 gs_dump指定schema下全部表结构信息备份 gs_dump database_name -U username -p port -F c -s -n schema_name -f schema.sqldatabase_name&#xff1a;数据库名&#xff0c;要备份的数据库名称 username&#xff1a;用户名&#xff0c;数据…...

编程日记 2023/10/16 2:59:45

干货：如何在前端统计用户访问来源？

在前端统计用户访问来源是一个常见的需求&#xff0c;通过获取访问来源信息&#xff0c;我们可以了解用户是通过直接访问、搜索引擎、外部链接等途径进入我们的网站或应用。下面是一个详细的介绍&#xff0c;包括方法和实现步骤。 一、获取HTTP Referer HTTP Referer是HTTP请…...

编程日记 2023/10/16 2:57:43

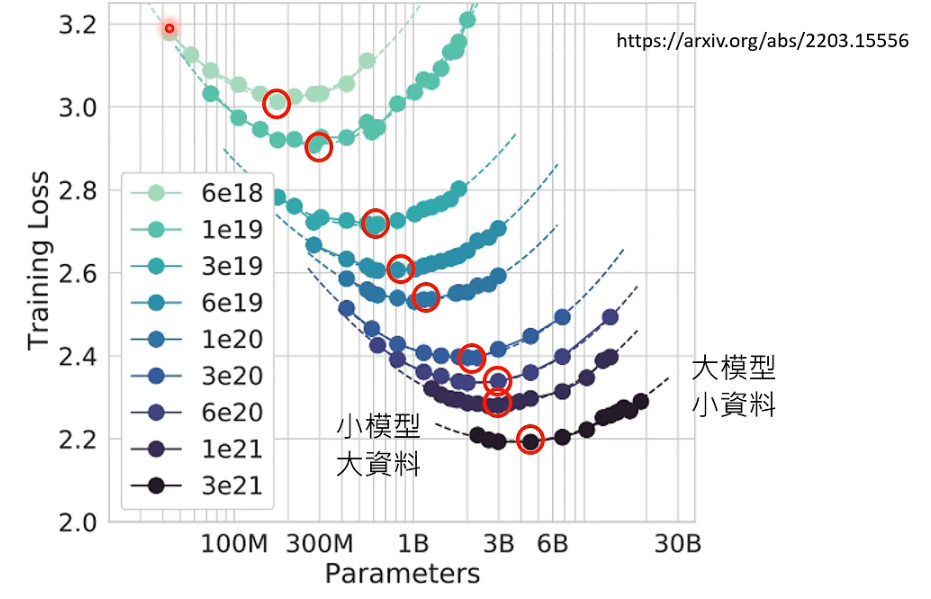
李宏毅生成式AI课程笔记（持续更新

01 ChatGPT在做的事情 02 预训练&#xff08;Pre-train&#xff09; ChatGPT G-Generative P-Pre-trained T-Transformer GPT3 ----> InstructGPT&#xff08;经过预训练的GPT3&#xff09; 生成式学习的两种策略 我们在使用ChatGPT的时候会注意到&#xff0c;网站上…...

编程日记 2023/10/16 2:56:42

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/1 9:48:47

376. Wiggle Subsequence

376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

编程新知 2025/12/9 1:33:12

2025 后端自学UNIAPP【项目实战：旅游项目】6、我的收藏页面

代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口&#xff08;适配服务端返回 Token&#xff09; export const login async (code, avatar) > {const res await http…...

编程新知 2025/12/14 8:37:22

工业自动化时代的精准装配革新：迁移科技3D视觉系统如何重塑机器人定位装配

AI3D视觉的工业赋能者 迁移科技成立于2017年&#xff0c;作为行业领先的3D工业相机及视觉系统供应商&#xff0c;累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成&#xff0c;通过稳定、易用、高回报的AI3D视觉系统&#xff0c;为汽车、新能源、金属制造等行…...

编程新知 2025/11/25 4:59:47

汇编常见指令

汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX&#xff08;不访问内存&#xff09;XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

编程新知 2025/11/4 20:56:54

多模态大语言模型arxiv论文略读（108）

CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题&#xff1a;CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者&#xff1a;Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

编程新知 2025/12/15 1:06:25

ios苹果系统，js 滑动屏幕、锚定无效

现象&#xff1a;window.addEventListener监听touch无效&#xff0c;划不动屏幕&#xff0c;但是代码逻辑都有执行到。 scrollIntoView也无效。 原因&#xff1a;这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作&#xff0c;从而会影响…...

编程新知 2025/12/4 2:37:03

Python 包管理器 uv 介绍

Python 包管理器 uv 全面介绍 uv 是由 Astral&#xff08;热门工具 Ruff 的开发者&#xff09;推出的下一代高性能 Python 包管理器和构建工具&#xff0c;用 Rust 编写。它旨在解决传统工具&#xff08;如 pip、virtualenv、pip-tools&#xff09;的性能瓶颈&#xff0c;同时…...

编程新知 2025/12/12 23:11:21

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2025/12/12 10:34:36

接口自动化测试：HttpRunner基础

相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具&#xff0c;支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议&#xff0c;涵盖接口测试、性能测试、数字体验监测等测试类型…...

编程新知 2025/11/30 2:35:09