vqvae简单实战,利用vqvae来提升模型向量表达
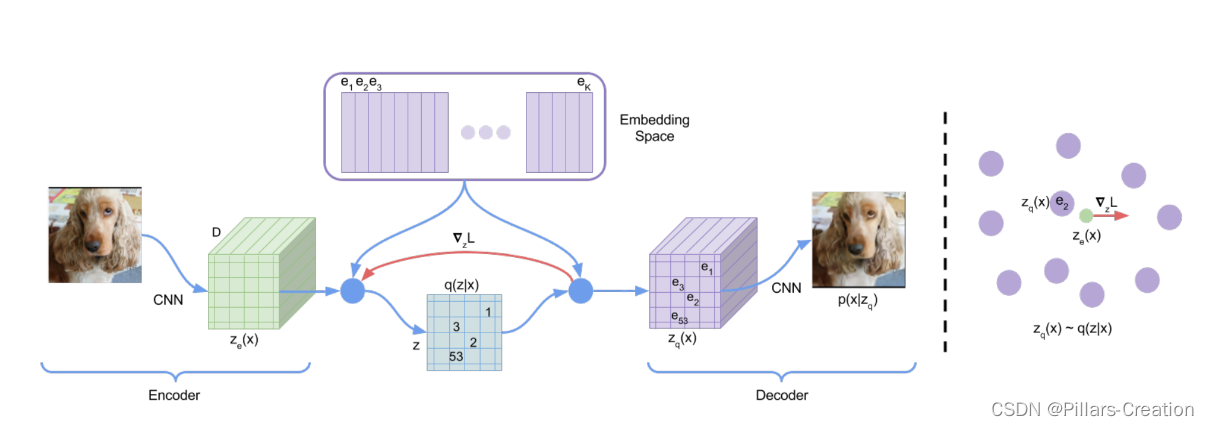
最近CV领域各种大模型在图像生成领域大发异彩,比如这两年大火的dalle系列模型。在这些模型中用到一个基础模型vqvae,今天我们写个简单实现来了解一下vqvae的工作原理。vqvae原始论文连接https://arxiv.org/pdf/1711.00937.pdf
1,代码
首先我们直接来看代码实现,完整代码GitHub - Pillars-Creation/vqvae: 使用vqvae 进行用户和物品冷启动
def vector_quantizer(self, z):# 将 z 的形状更改为 [batch_size, embedding_dim, 1]z_flat = z.view(-1, self.codebook_dim, 1)# 计算 z_flat 两两相乘的结果z_flat = torch.matmul(z_flat, z_flat.transpose(1, 2))z_flat = torch.sqrt(z_flat)# 计算z_flat中每个潜在向量与码本中所有向量之间的欧几里得距离distances = torch.cdist(z_flat, self.codebook)# 计算与每个潜在向量z最接近的码本向量的索引codebook_indices = torch.argmin(distances, dim=-1)# 使用codebook_indices从码本中检索与原始潜在向量z最接近的离散潜在向量z_qone_hot = F.one_hot(codebook_indices, self.codebook_size).type(z_flat.dtype)z_q = torch.matmul(one_hot, self.codebook)# 提取 z_q 的对角线元素并将它们相加以还原为形状为 [batch_size, emb] 的张量z_q = torch.diagonal(z_q, dim1=1, dim2=2)# 计算VQ损失,vq_loss为标量vq_loss = torch.mean(torch.square(z_q.detach() - z))commit_loss = torch.mean(torch.square(z.detach() - z_q))vq_loss += self.commitment_cost * commit_loss# Apply the Straight-Through Estimator (STE) trickz_q = z + (z_q - z).detach()# 计算困惑度avg_probs = torch.mean(one_hot, dim=0)perplexity = torch.exp(-torch.sum(avg_probs * torch.log(avg_probs + 1e-10)))# VQ-VAE Decoderz_q = z_q.view(z.shape)return z_q, vq_loss, perplexity2,为什么是vqvae,
要回答这个问题,我们看看vqvae论文里作者认为和传统vae模型的关键差异点。从论文可以看到作者认为关键差异点有两个一个是使用了离散编码,一个是动态的学习先验分布

离散编码
- VAE通过在编码器中引入隐变量(通常是高斯分布的样本)来建模数据的潜在分布。这种连续性的隐空间使得VAE在生成新样本时更加灵活。通过在隐空间中进行插值或随机采样,可以生成具有连续变化的新样本。但是VAE模型存在一个问题是后验奔溃
- 后验奔溃是指在训练过程中,编码器学到的潜在表示几乎没有包含输入数据的任何有用信息,而解码器主要依赖于其自身来生成数据。这种情况下,VAE 的生成性能会受到影响,因为潜在空间没有学到有效的数据表示。
- 在VQ-VAE中,编码器将输入数据映射到一个离散的隐藏,将编码器的输出与一个称为码本(codebook)的离散向量集进行匹配来实现的。使用一个离散编码表来表达连续分布。这种离散的隐藏表示具有一些优势,例如更高的表示能力和更好的泛化性能。
动态的学习先验分布
这块比较直观,在传统的 VAE 中,先验分布通常是一个固定的分布,例如标准正态分布。这意味着潜在变量应该遵循这个固定的分布,这是一个静态的约束。然而,在 VQ-VAE 中,先验分布是从数据中学习的,这意味着它可以根据数据的特点自适应地改变。这个学习的先验分布是通过优化码本中的离散向量来实现的。
在训练过程中,码本中的向量会根据输入数据和重构误差进行更新,从而学习到一个更适合表示数据的离散潜在空间。因此,当我们说 VQ-VAE 中的先验是学习的而不是静态的,潜在空间(即码本)可以根据数据自适应地调整。
3,代码里几个注意点
1,Straight-Through Estimator (STE) trick
vqvae因为要和codebook 取argmin,由于argmin不可导。所以要用STE技术。
STE是一种用于训练离散变量(例如二值变量)的神经网络的技巧。源于Benjio的论文《Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation》
Straight-Through的思想分两个部分,
前向传播的时候可以用想要的变量(哪怕不可导),
而反向传播的时候,用你自己为它所设计的梯度。
根据这个思想,我们设计的目标函数是:
其中detach()是stop gradient的意思。这样一来,前向传播计算(求loss)的时候,就直接等价于decoder(z+zq−z)=decoder(zq),然后反向传播(求梯度)的时候,由于zq−z不提供梯度,所以它也等价于decoder(z),这个就允许我们对encoder进行优化了。
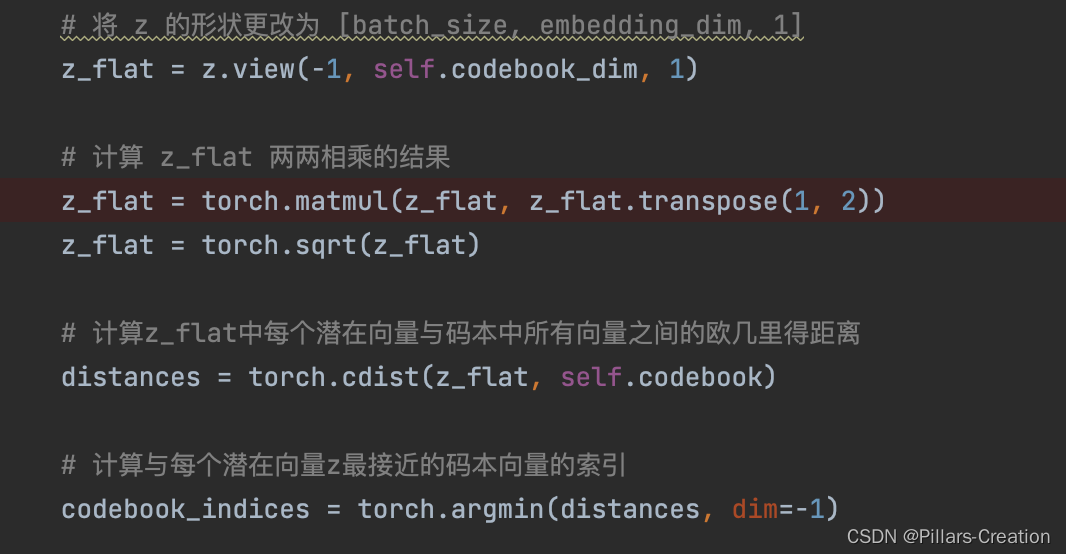
2,codebook
在cv里码本对应的encoder是卷积完的三维机构,如果我们是优化ID向量只有一维,需要做个转换把一维变成二维,这里可以用卷积,也可以把向量两两相乘变成二维结构,这样的好处是一方面方便我们把每一行当作一个向量和codebook求对应,另一方面两两相乘也可以理解为一种特征交叉,提升了向量的表达。如代码中实现
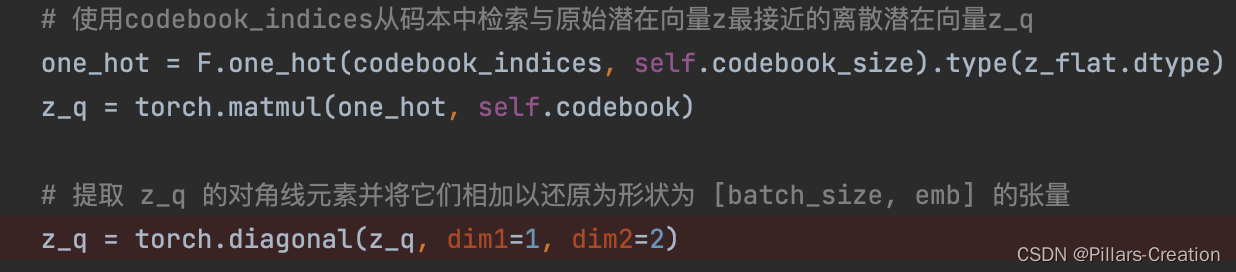
3,提取对角线元素,
因为刚刚encode的时候我们做了两两相乘生成了个二维矩阵,所以从codebook中取得映射后,也是个二维矩阵,我们对应的取对角线值,把向量还原为一维,对应代码
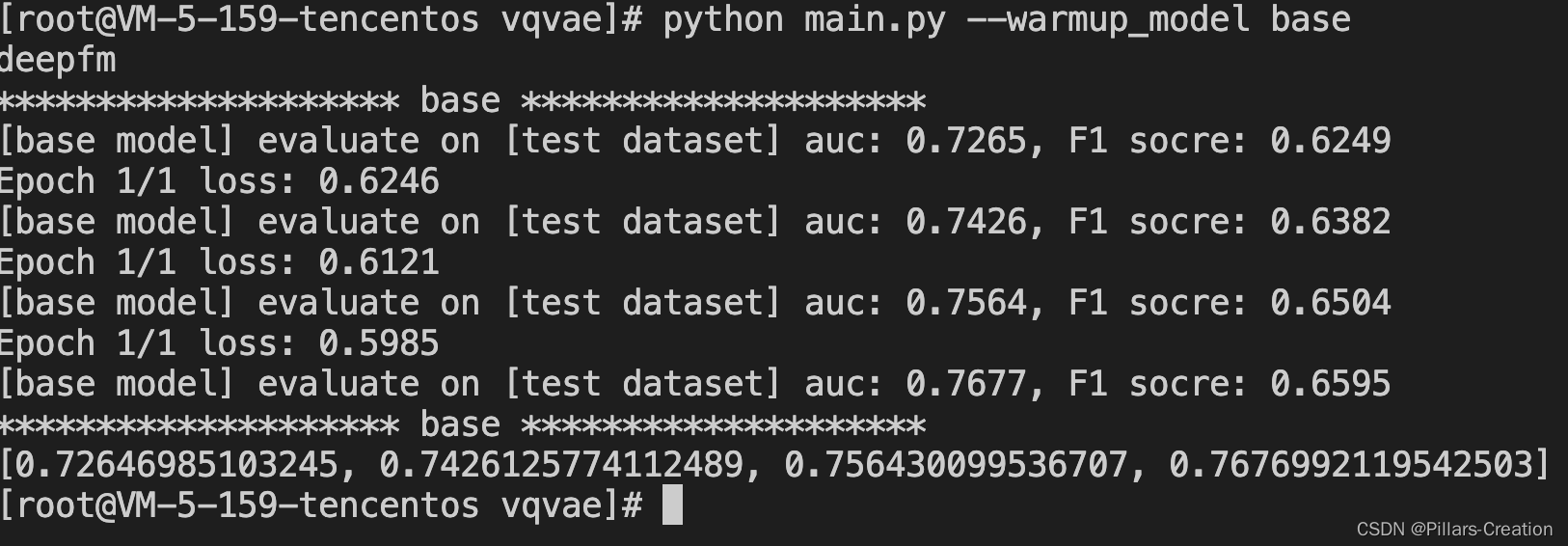
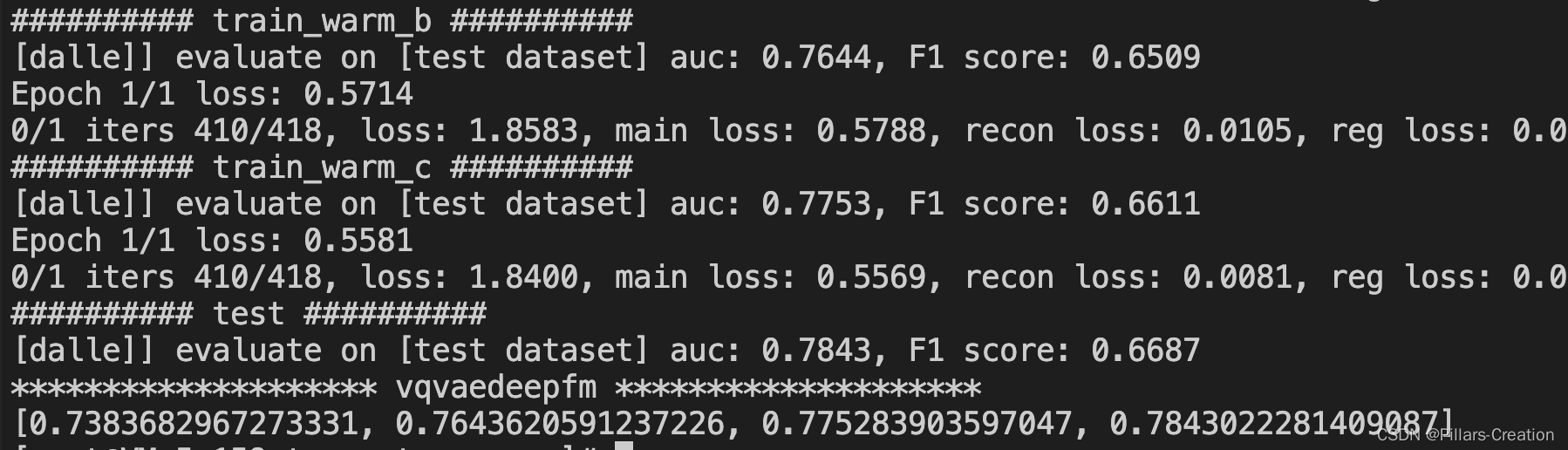
4.实验效果
在movilen的数据集上对物品ID做了增强,可以看到效果还是不错的
相关文章:

vqvae简单实战,利用vqvae来提升模型向量表达
最近CV领域各种大模型在图像生成领域大发异彩,比如这两年大火的dalle系列模型。在这些模型中用到一个基础模型vqvae,今天我们写个简单实现来了解一下vqvae的工作原理。vqvae原始论文连接https://arxiv.org/pdf/1711.00937.pdf 1,代码 首先我们…...
idea禁用双击ctrl
Run anything | IntelliJ IDEA Documentation Disable double modifier key shortcuts...
记使用docker部署项目出现问题
我的docker-compose.yml内容如下: version: "3" services:my_server:build: .restart: alwaysdepends_on:mysql:condition: service_startedports:- 9999:9999links:- mysqlmysql:image: mysql:latest # mysql:oraclerestart: alwayscontainer_name: mys…...

EDU挖掘
1.信息搜集2.漏洞挖掘 1.信息搜集 没事干,准备找个证书站挖挖看,没想到碰到一个小通用系统。 看样子还挺多功能可以测, 这里利用F12 查看前端源码js 或者css文件,直接用hunter或者fofa搜索到同一类型的网站。 Hunter语法&#…...

机器人制作开源方案 | 杠杆式6轮爬楼机器人
1. 功能描述 本文示例将实现R281b样机杠杆式6轮爬楼机器人爬楼梯的功能(注意:演示视频中为了增加轮胎的抓地力,在轮胎上贴了双面胶,请大家留意)。 2. 结构说明 杠杆式6轮爬楼机器人是一种专门用于爬升楼梯或不平坦地面…...

报错——warning: ignoring JAVA_HOME=/home/jdk/jdk1.8.0_281; using bundled JDK
我使用了es的8.3.0版本,但es从7.17版本以后不再支持jdk1.8了,需要进行JDK的版本升级,或者降低es的版本。 es和jdk对比版本...

【Java8】java.time 根据日期获取年初年末、月初月末、日初日末
目录 年初年末月初月末3. 日初日末 记录日常开发中的常用的日期转换代码,算是一篇Java 8时间API使用实操的简短总结文。 下文中,都以LocalDateTime为例,在不声明的情况下如下方法一般都适用于Java8中LocalDate、LocalDateTime、OffsetDateTi…...

【LeetCode: 137. 只出现一次的数字 II | 位运算 | 哈希表】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

「深入探究Web页面生命周期:DOMContentLoaded、load、beforeunload和unload事件」
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 引言 1. DOMContentLoaded 1.1 属性 1.2 A…...
SpringMVC源码分析(一)启动流程分析
a、SpringMVC 在启动过程中主要做了什么事情? SpringMVC在启动过程中是什么时候解析web.xml文件的,又是什么时候初始化9大内置对象的? <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://xml…...

ARM 10.12
设置按键中断,按键1按下,LED亮,再按一次,灭 按键2按下,蜂鸣器响。再按一次,不响 按键3按下,风扇转,再按一次,风扇停 src/key.c #include"key.h"//按键3的配…...

vue-rouer 路由
安装/配置: //进入项目目录:(在搭建项目的时候安装了) cnpm install vue-router --save旧版路由 需要自己配置 //项目中载入,一般在main.js中载入:import VueRouter from vue-routerVue.use(VueRouter)let router new VueRouter({}) //其中配置路径和地址//在Vue中引入:n…...

元数据的前世今生
什么是元数据 元数据(Metadata)是描述数据的数据。它是一组信息,用于描述数据的特征、属性、结构和内容,以便更好地管理、理解、组织和使用数据。让人们能够清楚拥有什么数据、代表什么、源自何处、如何在系统中移动,以及哪些人可以使用源数据,如何使用。 元数据通常包…...

Python实现简易过滤删除数字的方法
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 如果想从一个含有数字,汉字,字母的列表中滤除仅含有数字的字符, 当然可以采取正则表达式来完成,但是有点太麻烦了…...
软件测试定位bug方法+定位案例(详解)
1、问题bug定位技巧 首先,作为开发也好,测试也好,定位问题有一个总的思路,而这个思路是和数据的走向一致的。 大致是这样: 用户层面问题 -> Web页面/软件界面 -> 中间件 -> 后端服务 -> 代码 -> 数据…...

【算法练习Day21】组合剪枝
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 组合剪枝总结: …...

NPM相关命令
临时使用 npm --registry https://registry.npm.taobao.org install 包名2.永久设置为淘宝镜像 npm config set registry https://registry.npm.taobao.org3.换回国外官方源 npm config set registry https://registry.npmjs.org4.查看使用的源地址 npm config get registr…...
Kubernetes 集群部署 Prometheus 和 Grafana
Kubernetes 集群部署 Prometheus 和 Grafana 文章目录 Kubernetes 集群部署 Prometheus 和 Grafana一.部署 node-exporter1.node-exporter 安装2.部署 node-exporter 二.部署Prometheus1.Prometheus 安装和配置(1)创建 sa 账号,对 sa 做 rbac…...

【算法-动态规划】零钱兑换 II-力扣 518
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...
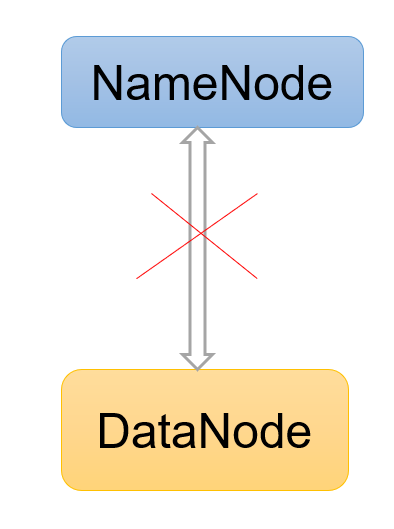
Hadoop3教程(六):HDFS中的DataNode
文章目录 (63)DataNode工作机制(64)数据完整性(65)掉线时限参数设置参考文献 (63)DataNode工作机制 DataNode内部存储了一个又一个Block,每个block由数据和数据元数据组…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
