数据在内存中的存储(2)
文章目录
- 3. 浮点型在内存中的存储
- 3.1 一个例子
- 3.2 浮点数存储规则
3. 浮点型在内存中的存储
常见的浮点数:
3.14159
1E10 ------ 1.0 * 10^10
浮点数家族包括: float、double、long double 类型
浮点数表示的范围:float.h中定义
3.1 一个例子
浮点数存储的例子:
#include <stdio.h>int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}
输出的结果是什么呢?
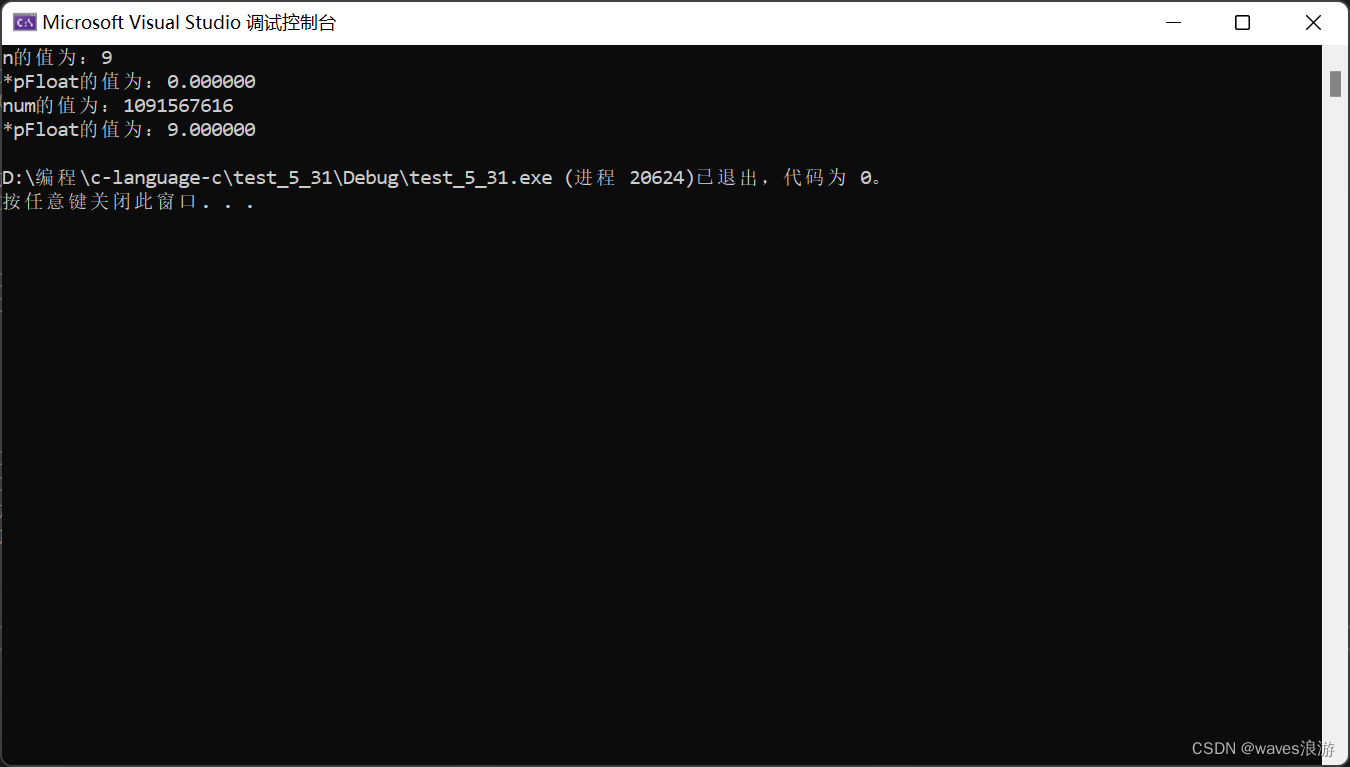
通过输出的结果,我们可以得知:一个数以整型的形式放进去,再以整型或浮点型的形式拿出来,结果是不一样的;一个数以浮点型的形式放进去,再以整型或浮点型的形式拿出来,结果也是不一样的。因此,我们可以推出:整型和浮点型在内存中的存储方式是有差异的!
3.2 浮点数存储规则
num 和 *pFloat 在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?
要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法。
详细解读:
根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^S * M * 2^E
- (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
- M表示有效数字,大于等于1,小于2。
- 2^E表示指数位。
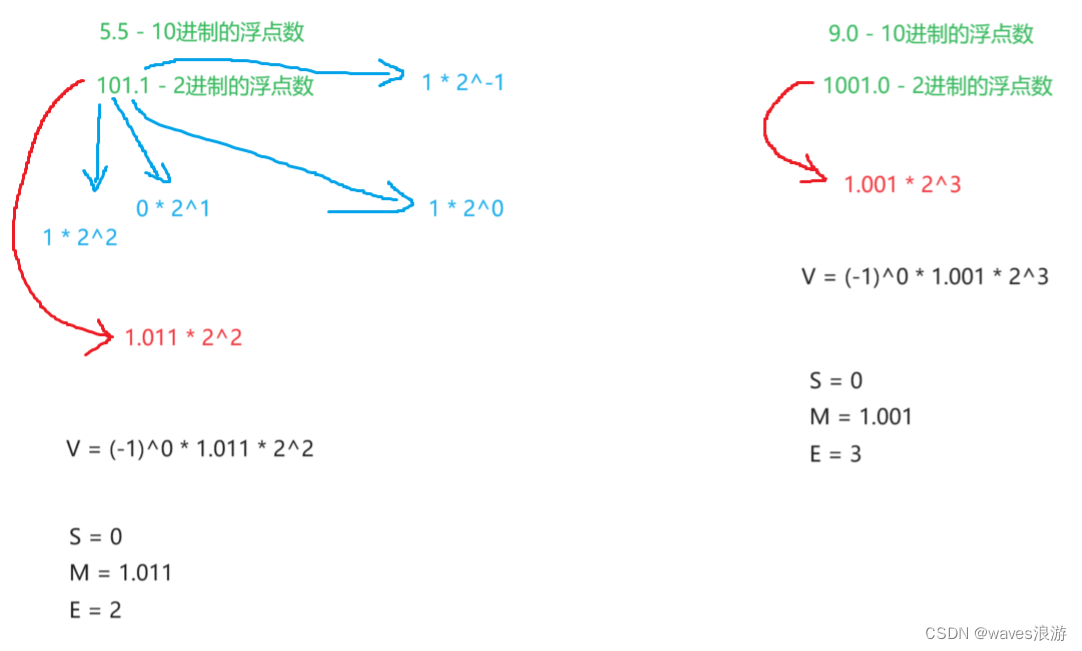
IEEE 754规定:
对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位为有效数字M。

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
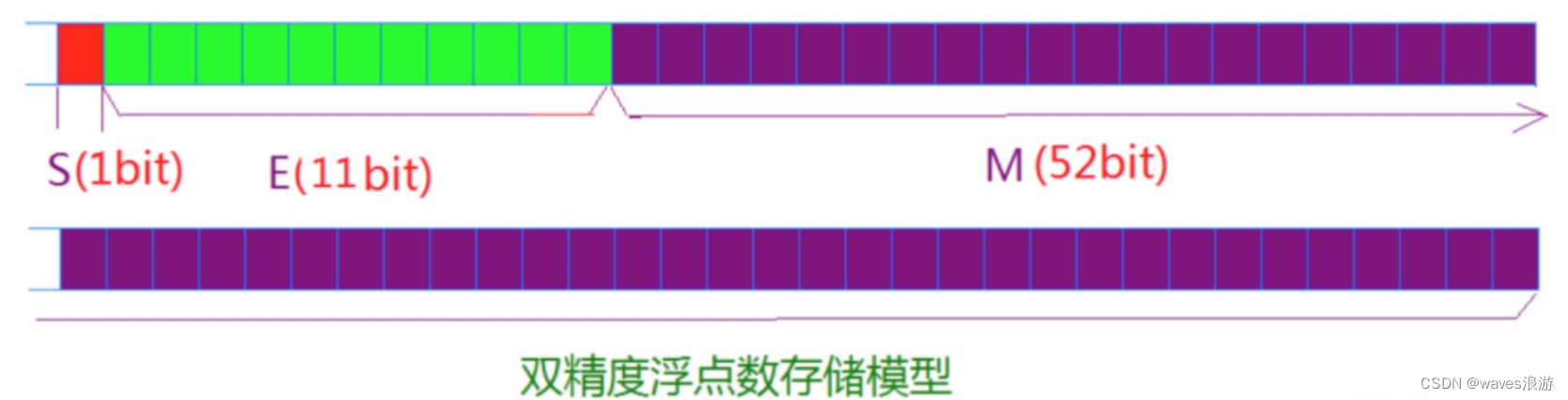
IEEE 754对有效数字M和指数E,还有一些特别规定:
前面说过,1≤M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂:
首先,E为一个无符号整数(unsigned int)。这意味着,如果E为8位,它的取值范围为0 ~ 255;如果E为11位,它的取值范围为0 ~ 2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
int main()
{float f = 5.5;//101.1//1.011 * 2^2//(-1)^0 * 1.011 * 2^2//S = 0//M = 1.011//E = 2//01000000101100000000000000000000//0x40b00000return 0;
}
然后,指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1。
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)。
通过以上讲解,我们就可以解释一开始的代码了:
#include <stdio.h>int main()
{int n = 9;//00000000000000000000000000001001float* pFloat = (float*)&n;printf("n的值为:%d\n", n);//9printf("*pFloat的值为:%f\n", *pFloat);//0.000000//0 00000000 00000000000000000001001//S E M//E在内存中是全0//0 -126 0.00000000000000000001001//(-1)^0 * 0.00000000000000000001001 * 2^-126*pFloat = 9.0;//1001.0///1.001 * 2^3//(-1)^0 * 1.001 * 2^3//S=0 M=1.001 E=3//01000001000100000000000000000000printf("num的值为:%d\n", n);//1091567616printf("*pFloat的值为:%f\n", *pFloat);//9.000000return 0;
}
相关文章:

数据在内存中的存储(2)
文章目录 3. 浮点型在内存中的存储3.1 一个例子3.2 浮点数存储规则 3. 浮点型在内存中的存储 常见的浮点数: 3.14159 1E10 ------ 1.0 * 10^10 浮点数家族包括: float、double、long double 类型 浮点数表示的范围:float.h中定义 3.1 一个例…...

软件工程与计算总结(十三)详细设计中的模块化与信息隐藏
一.模块化与信息隐藏思想 1.设计质量 好的设计要着重满足以下3方面:可管理性、灵活性、可理解性好的设计需要侧重于间接性和可观察性——简洁性使得系统模块易于管理(理解和分解)、开发(修改与调试)和复用。实践者都…...

RF学习——器件的非线性失真分析
在大信号激励下的射频系统 在电路中,如果激励信号的幅度不可忽视,那么就会产生非线性失真。如二极管,晶体管等电路元件的特性在大信号激励下回变得非线性,输入和输出的形状不同,产生失真。 在功率放大器PA中,随着传输给负载的功率增大而迅速增大,传递功率的规格要始终考…...

SUB-1G SOC芯片DP4306F 32 位 ARM Cortex-M0+内核替代CMT2380F32
DP4306F是一款高性能低功耗的单片集成收发机,集成MO核MCU,工作频率可覆盖200MHiz^ 1000MHz。 支持230/408/433/470/868/915频段。该芯片集成了射频接收器、射频发射器、频率综合器、GFSK调制器、GFSK解调器等功能模块。通过SPI接口可以对输出功率、频道选…...

接收请求地址下载并输出文件流实现
代码: import httpxfrom datetime import datetime from io import BytesIO from fastapi.responses import StreamingResponse@router.get("/download", tags=["下载"]) async...
【iOS】——用单例类封装网络请求
文章目录 一、JSONModel1.JSONModel的简单介绍2.JSONModel的使用 二、单例类和Block传值 一、JSONModel 1.JSONModel的简单介绍 JSONModel一个第三方库,这个库用来将网络请求到的JSON格式的数据转化成Foundation框架下的Model类的属性,这样我们就可以直…...

再学Blazor——概述
简介 Blazor 是一种 .NET 前端 Web 框架,同时支持服务器端呈现和客户端交互性。 使用 C# 语言创建丰富的交互式 UI共享前后端应用逻辑可以生成混合桌面和移动应用受益于 .NET 的性能、可靠性和安全性需要有 HTML、CSS、JS 相关基础(开发 UI 框架的话&a…...

Ceph运维笔记
Ceph运维笔记 一、基本操作 ceph osd tree //查看所有osd情况 其中里面的weight就是CRUSH算法要使用的weight,越大代表之后PG选择该osd的概率就越大 ceph -s //查看整体ceph情况 health_ok才是正常的 ceph osd out osd.1 //将osd.1踢出集群 ceph osd i…...
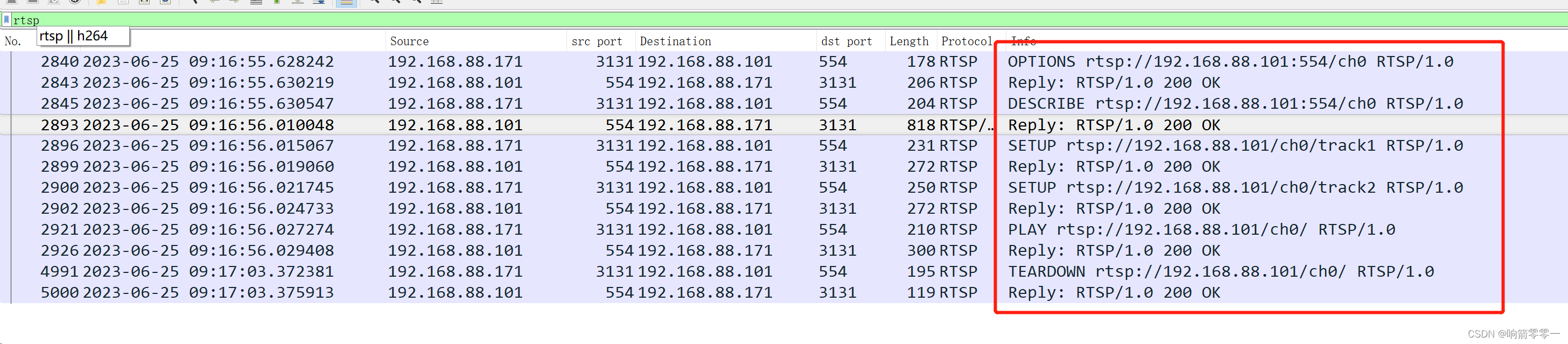
RTSP协议
1 前言 RTSP协议作为音视频实时监控一个非常重要的协议,具有非常广泛的应用。RTSP由RFC 2326规范化,它允许客户端通过请求不同的媒体资源来控制流媒体服务器。RTSP是一种应用层协议,通常基于TCP连接,用于建立和控制媒体会话。这使…...

Maven系列第6篇:生命周期和插件详解?
maven系列目标:从入门开始开始掌握一个高级开发所需要的maven技能。 这是maven系列第6篇。 整个maven系列的内容前后是有依赖的,如果之前没有接触过maven,建议从第一篇看起,本文尾部有maven完整系列的连接。 前面我们使用maven…...

【通义千问】大模型Qwen GitHub开源工程学习笔记(4)-- 模型的量化与离线部署
摘要: 量化方案基于AutoGPTQ,提供了Int4量化模型,其中包括Qwen-7B-Chat和Qwen-14B-Chat。更新承诺在模型评估效果几乎没有损失的情况下,降低存储要求并提高推理速度。量化是指将模型权重和激活的精度降低以节省存储空间并提高推理速度的过程。AutoGPTQ是一种专有量化工具。…...

2022最新版-李宏毅机器学习深度学习课程-P23 为什么用了验证集结果还是过拟合
用了验证集还有可能会过拟合 这个片段可以从理论上证明这一点 以上整个挑选模型的过程也可以想象为一种训练。 把三个模型导出的最小损失公式看成一个集合,现在要做的就是在这个集合中找到某个h(此处可以视为训练),使得在验证集…...

Spring Cloud Alibaba—Sentinel 控制台安装
1、Sentinel 控制台包含如下功能: 查看机器列表以及健康情况:收集 Sentinel 客户端发送的心跳包,用于判断机器是否在线。 监控 (单机和集群聚合):通过 Sentinel 客户端暴露的监控 API,定期拉取并且聚合应用监控信息,最…...

基于动物迁徙优化的BP神经网络(分类应用) - 附代码
基于动物迁徙优化的BP神经网络(分类应用) - 附代码 文章目录 基于动物迁徙优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.动物迁徙优化BP神经网络3.1 BP神经网络参数设置3.2 动物迁徙算法应用 4.测试结果…...

一键搞定!黑群晖虚拟机+内网穿透实现校园公网访问攻略!
文章目录 前言本教程解决的问题是:按照本教程方法操作后,达到的效果是前排提醒: 1. 搭建群晖虚拟机1.1 下载黑群晖文件vmvare虚拟机安装包1.2 安装VMware虚拟机:1.3 解压黑群晖虚拟机文件1.4 虚拟机初始化1.5 没有搜索到黑群晖的解…...

【C语言】——通讯录(静态-动态增长-文件储存)
目录 前言: 一:整体框架 关于通讯录结构体的创建 二:通讯录的功能实现(静态) 2.1初始化通讯录 2.2增加联系人 2.3打印通讯录 2.4删除联系人 2.5 查找联系人 2.6修改联系人 2.7排序联系人 三:通…...
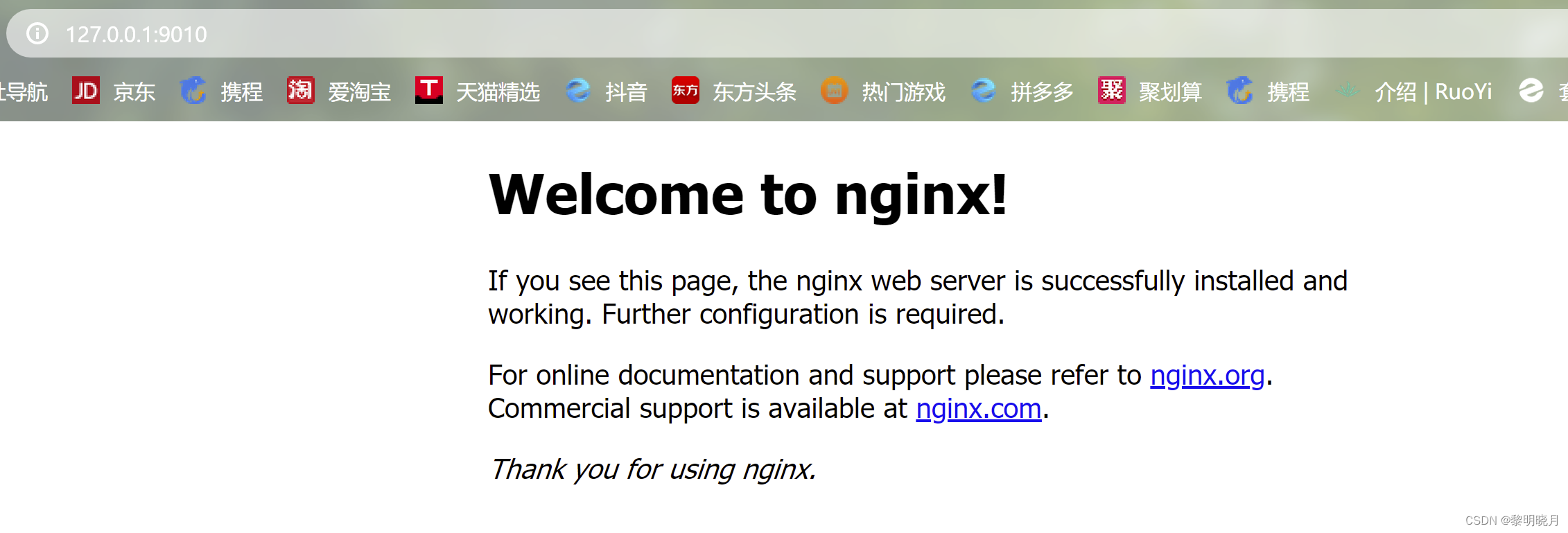
win10安装nginx及简单使用(命令)
下载 下载地址:http://nginx.org/en/download.html 使用 解压 更改配置 conf目录下nginx.conf 修改为未被占用的端口,地址改成你的地址 server {# 监听端口 listen 9010;# 地址 server_name 127.0.0.1;# 静态资源location / {root html;i…...

【农业生产系统模型】基于R语言APSIM模型进阶应用与参数优化、批量模拟实践技术
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...

金融数学方法:梯度下降法
1.算法介绍 梯度下降法是一种常用的优化算法,其通过沿着梯度下降的方向迭代寻找局部极小值。如果沿着梯度上升的方向迭代,就可以找到极大值。 在梯度下降法中,我们首先需要选择一个初始点 x 0 x_0 x0作为起始位置,然后计算当前位…...

1031 查验身份证
一.问题: 一个合法的身份证号码由17位地区、日期编号和顺序编号加1位校验码组成。校验码的计算规则如下: 首先对前17位数字加权求和,权重分配为:{7,9,10,5,8,4…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
