基于Eigen的位姿转换
位姿中姿态的表示形式有很多种,比如:旋转矩阵、四元数、欧拉角、旋转向量等等。这里基于Eigen实现四种数学形式的相互转换功能。本文利用Eigen实现上述四种形式的相互转换。我这里给出一个SE3(4*4)(先平移、再旋转)的构建方法:
Eigen::Isometry3f T1 = Eigen::Isometry3f::Identity(); // 这一句千万别掉
// <1> 初始化R
Eigen::Matrix3f R;
// 按照 ZYX 顺序旋转
R = Eigen::AngleAxisf(3.14159 / 4, Eigen::Vector3f::UnitX()) *Eigen::AngleAxisf(0, Eigen::Vector3f::UnitY()) *Eigen::AngleAxisf(0, Eigen::Vector3f::UnitZ());
// <2> 初始化t
Eigen::Vector3f t(0.0, 0.0, 4.0);
// <3> 构建T = (R|t)
T1.rotate(R);
T1.pretranslate(t); // 这一句别搞错
//T1.translate(t);
std::cout << "T1 = " <<T1.matrix() <<std::endl;打印结果:
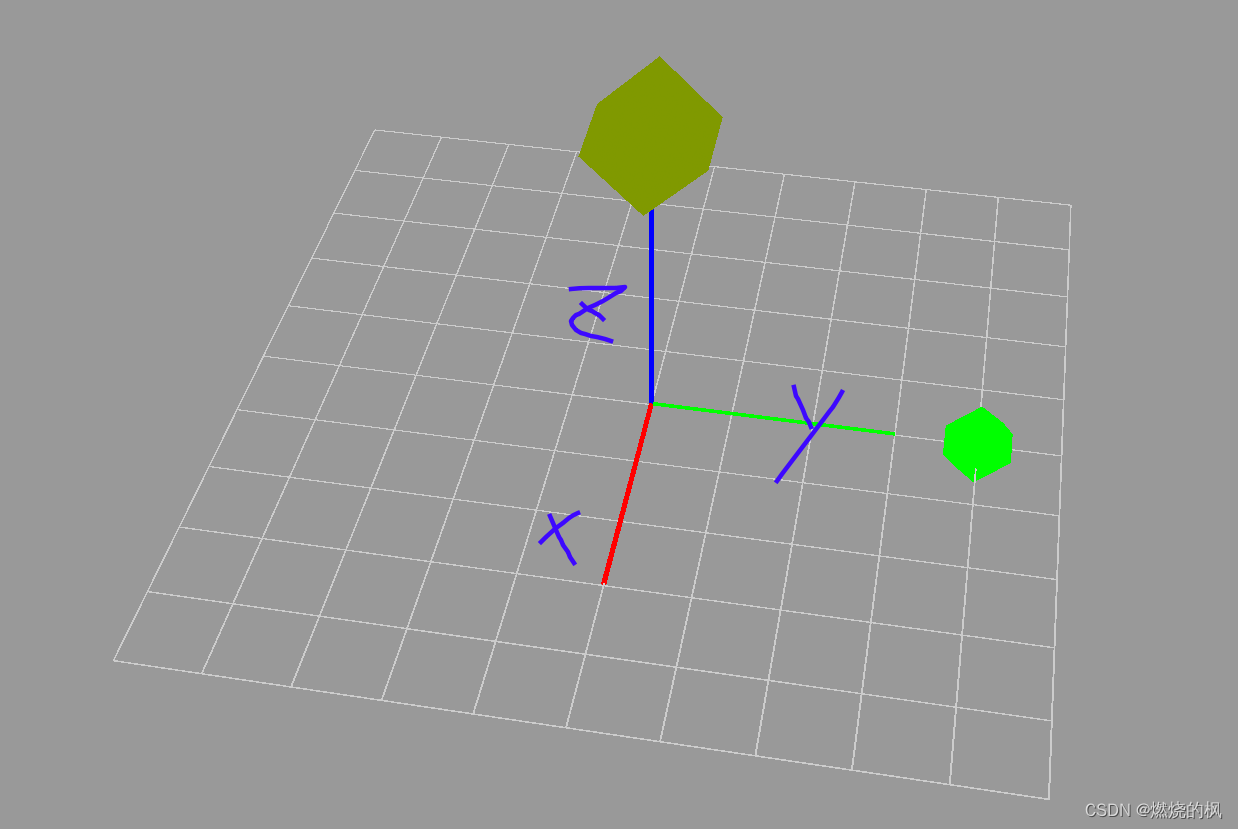
T1 = 1 0 0 00 0.707107 -0.707106 00 0.707106 0.707107 40 0 0 1下面的黄色立方体,相对坐标系位置为:(0 0 4),绕x轴旋转pi /4,得到绿色立方体
以下是在本地word中笔记的截图:






Pose.h(类Pose声明)
#pragma once
#ifndef POSE_H
#define POSE_H#include<Eigen/Core>
#include<Eigen/Geometry>// namespace Geometryclass Pose
{
public:Pose();Pose& operator= (const Pose& pose);// construct from rotationPose(const Eigen::Matrix3d& rotation);// construct from quaternionPose(const Eigen::Quaterniond& quaternion);// construct from angle axisdPose(const Eigen::AngleAxisd& angle_axis);// construct from euler anglePose(const Eigen::Vector3d& euler_angle);~Pose();// return rotationEigen::Matrix3d rotation() const;// return quaterniondEigen::Quaterniond quaternion() const;// return angle axisdEigen::AngleAxisd angle_axis() const;// return euler angleEigen::Vector3d euler_angle() const;private:Eigen::Matrix3d rotation_; // 旋转矩阵Eigen::Quaterniond quaternion_; // 四元数Eigen::AngleAxisd angle_axis_; // 角轴Eigen::Vector3d euler_angle_; // 欧拉角 roll(X轴) pitch(Y轴) yaw(Z轴)};// 姿态组合
Eigen::Isometry3d compose(const Eigen::Isometry3d& T1, const Eigen::Isometry3d& T2);// 求逆
Eigen::Isometry3d inverse(const Eigen::Isometry3d& T);#endif // !POSE_HPose.cpp(类Pose的实现)
#include "Pose.h"Pose::Pose()
{}Pose& Pose::operator= (const Pose& pose)
{this->rotation_ = pose.rotation();this->quaternion_ = pose.quaternion();this->angle_axis_ = pose.angle_axis();this->euler_angle_ = pose.euler_angle();return *this;
}//
Pose::Pose(const Eigen::Matrix3d& rotation) :rotation_(rotation),quaternion_(Eigen::Quaterniond(rotation_)),angle_axis_(Eigen::AngleAxisd(rotation_)),euler_angle_(rotation_.eulerAngles(0, 1, 2))
{}Pose::Pose(const Eigen::Quaterniond& quaternion)
{quaternion.normalized();this->rotation_ = quaternion.toRotationMatrix();this->quaternion_ = Eigen::Quaterniond(rotation_);this->angle_axis_ = Eigen::AngleAxisd(rotation_);this->euler_angle_ = rotation_.eulerAngles(0, 1, 2);
}Pose::Pose(const Eigen::AngleAxisd& angle_axis) :rotation_(angle_axis),quaternion_(Eigen::Quaterniond(rotation_)),angle_axis_(Eigen::AngleAxisd(rotation_)),euler_angle_(rotation_.eulerAngles(0, 1, 2))
{}Pose::Pose(const Eigen::Vector3d& euler_angle) :rotation_(Eigen::AngleAxisd(euler_angle.x(), Eigen::Vector3d::UnitX()) * // note: ZYXEigen::AngleAxisd(euler_angle.y(), Eigen::Vector3d::UnitY()) *Eigen::AngleAxisd(euler_angle.z(), Eigen::Vector3d::UnitZ())),quaternion_(Eigen::Quaterniond(rotation_)),angle_axis_(Eigen::AngleAxisd(rotation_)),euler_angle_(rotation_.eulerAngles(0, 1, 2))
{}Pose::~Pose()
{}Eigen::Matrix3d Pose::rotation() const
{return this->rotation_;
}Eigen::Quaterniond Pose::quaternion() const
{return this->quaternion_;
}Eigen::AngleAxisd Pose::angle_axis() const
{return this->angle_axis_;
}Eigen::Vector3d Pose::euler_angle() const
{return this->euler_angle_;
}Eigen::Isometry3d compose(const Eigen::Isometry3d& T1, const Eigen::Isometry3d& T2)
{return T1 * T2;
}Eigen::Isometry3d inverse(const Eigen::Isometry3d& T)
{return T.inverse();
}test_pose.cpp
#include<iostream>
using namespace std;#include"Pose.h"
const double M_PI = 3.1415926535;// 对于同一个姿态,从不同的数学形式(旋转矩阵、四元数、欧拉角、角轴)构造类Pose
// 依次得到 pose1 pose2 pose3 pose4
void testClassPose(const Eigen::Matrix3d& R1)
{Pose pose1(R1);cout << "旋转矩阵 = " << endl; cout << pose1.rotation() << endl;cout << "欧拉角 = " << endl; cout << pose1.euler_angle().transpose()*(180 / M_PI) << endl;cout << "四元数 = " << endl; cout << pose1.quaternion().coeffs().transpose() << endl;cout << "角轴 = " << endl;cout << pose1.angle_axis().angle()* (180 / M_PI) <<" " << pose1.angle_axis().axis().transpose() <<endl;cout << "-----------------------------" << endl;Pose pose2(pose1.euler_angle());cout << "旋转矩阵 = " << endl; cout << pose2.rotation() << endl;cout << "欧拉角 = " << endl; cout << pose2.euler_angle().transpose()*(180 / M_PI) << endl;cout << "四元数 = " << endl; cout << pose2.quaternion().coeffs().transpose() << endl;cout << "角轴 = " << endl;cout << pose2.angle_axis().angle()* (180 / M_PI) << " " << pose2.angle_axis().axis().transpose() << endl;cout << "-----------------------------" << endl;Pose pose3(pose1.angle_axis());cout << "旋转矩阵 = " << endl; cout << pose3.rotation() << endl;cout << "欧拉角 = " << endl; cout << pose3.euler_angle().transpose()*(180 / M_PI) << endl;cout << "四元数 = " << endl; cout << pose3.quaternion().coeffs().transpose() << endl;cout << "角轴 = " << endl;cout << pose3.angle_axis().angle()* (180 / M_PI) << " " << pose3.angle_axis().axis().transpose() << endl;cout << "-----------------------------" << endl;Pose pose4 = pose3;cout << "旋转矩阵 = " << endl; cout << pose4.rotation() << endl;cout << "欧拉角 = " << endl; cout << pose4.euler_angle().transpose()*(180 / M_PI) << endl;cout << "四元数 = " << endl; cout << pose4.quaternion().coeffs().transpose() << endl;cout << "角轴 = " << endl;cout << pose4.angle_axis().angle()* (180 / M_PI) << " " << pose4.angle_axis().axis().transpose() << endl;cout << "-----------------------------" << endl;}// 测试求逆、compose等
void testTheOthers(Eigen::Matrix3d R1, Eigen::Vector3d t1,Eigen::Matrix3d R2, Eigen::Vector3d t2)
{// 初始化T1Eigen::Isometry3d T1 = Eigen::Isometry3d::Identity();T1.prerotate(R1); T1.pretranslate(t1);cout << "T1" << endl; cout << T1.matrix() << endl;// 初始化T2Eigen::Isometry3d T2 = Eigen::Isometry3d::Identity();T2.prerotate(R2); T2.pretranslate(t2);cout << "T2" << endl; cout << T2.matrix() << endl;// 求逆Eigen::Isometry3d T1_inverse = inverse(T1);cout << "T1_inverse = " << endl; cout << T1_inverse.matrix() << endl;// composeEigen::Isometry3d T12 = compose(T1, T2);cout << "T12 = " << endl; cout << T12.matrix() << endl;/*cout << "Rotation = " << endl;cout << T1.rotation() * T2.rotation() << endl;cout << "Translation = " << endl;cout << T1.rotation() * T2.translation() + T1.translation() << endl;*/}int main()
{Eigen::Matrix3d R1; //R1R1 = Eigen::AngleAxisd((30.0 / 180) * M_PI, Eigen::Vector3d::UnitX())*Eigen::AngleAxisd((25.0 / 180) * M_PI, Eigen::Vector3d::UnitY())*Eigen::AngleAxisd((27.0 / 180) * M_PI, Eigen::Vector3d::UnitZ());Eigen::Vector3d t1(1.2, 0.234, 2.3);//t1Eigen::Matrix3d R2; //R2R2 = Eigen::AngleAxisd((23.0 / 180) * M_PI, Eigen::Vector3d::UnitX())*Eigen::AngleAxisd((33.0 / 180) * M_PI, Eigen::Vector3d::UnitY())*Eigen::AngleAxisd((89.0 / 180) * M_PI, Eigen::Vector3d::UnitZ());Eigen::Vector3d t2(0.1, 0.4, 0.1); //t2// <1> test Class PosetestClassPose(R1);// <2> test halcon's apitestTheOthers(R1, t1, R2, t2);return 1;
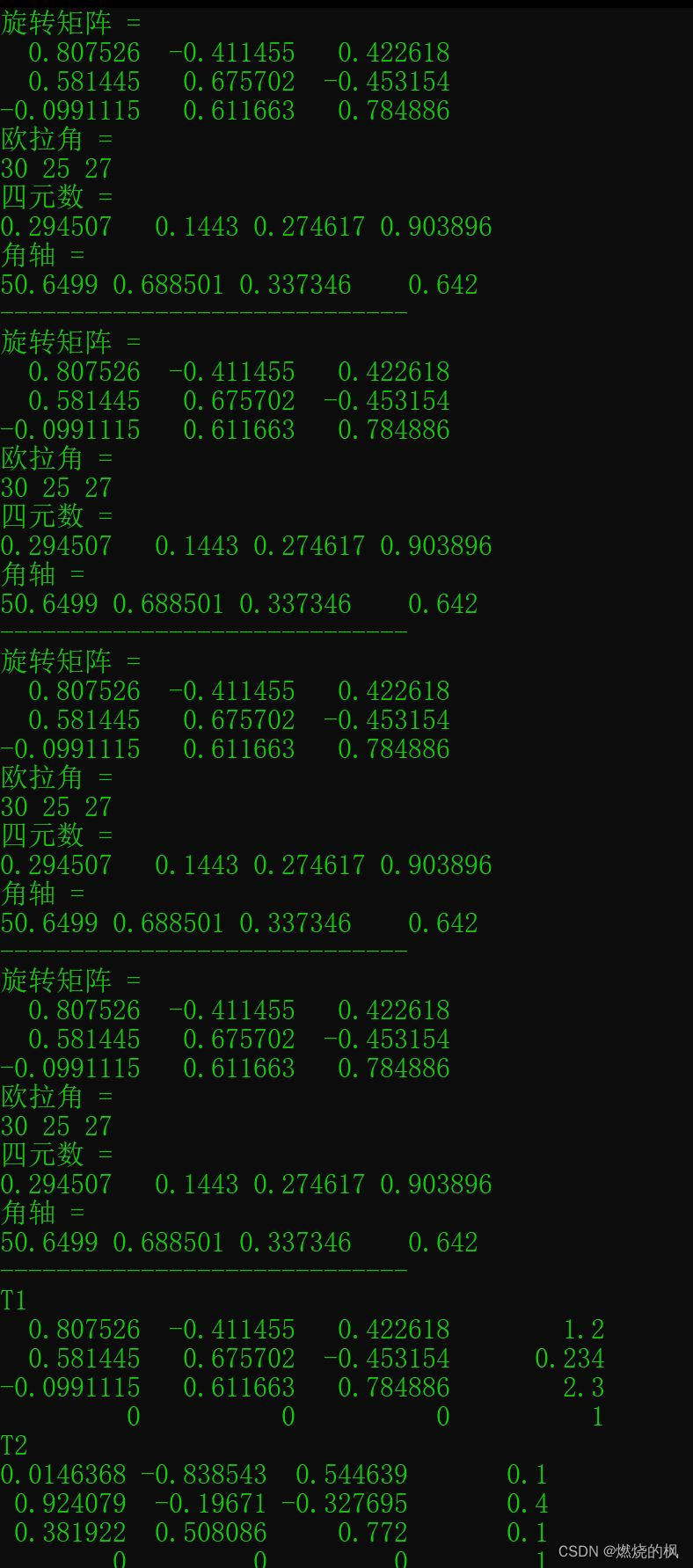
}可以看到,同一个姿态,不同的表达形式,他们之间相互转换之后结果数值一致。
写在最后,一个T为4×4的变换矩阵,如果旋转分量是欧式正交群,那个这个T为:欧式变换;否者为:仿射变换。如果一个旋转矩阵,不是SO3,那么可以将其转为四元数,接着归一化,再转为旋转矩阵,这样结果就属于SO3。同理,如果一个四元数,最好对齐进行归一化处理,再转为其他形式。例如:构造函数Pose(const Eigen::Quaterniond& quaternion); 其实现中比其他构造函数多了归一化这一步骤;即:quaternion.normalized();
请看测试案例test3(),我们在第4或第5行进行四元数归一化,那么24行打印出来的矩阵就是单位阵。(不归一化,则不是单位阵)
void test3()
{Eigen::Quaterniond q = { 0.1,0.35,0.2,0.3 };//q.normalize();Eigen::Matrix3d R = q.normalized().toRotationMatrix();cout << "R = " << endl;cout << R << endl;cout << endl;Eigen::Matrix3d R_transpose = R.transpose();cout << "R.transpose = " << endl;cout << R_transpose << endl;cout << endl;Eigen::Matrix3d R_inverse = R.inverse();cout << "R.inverse = " << endl;cout << R_inverse << endl << endl;cout << endl;Eigen::Matrix3d ret = R * R.transpose();cout << "ret = " << endl;cout << ret << endl << endl;cout << endl;
}运行结果:
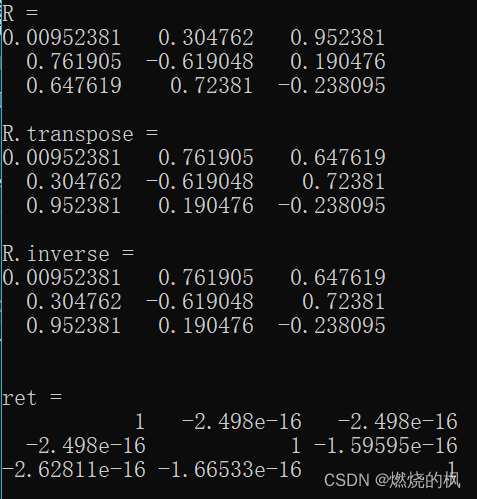
现在,如果给定一个旋转矩阵(如果你是随机测试,请你参考博客开始部分公式,每个元素是有取值范围的,给出的数字不要太离谱);如下测试案例test4。第8行在底层有四元数归一化操作,所以你看下面效果图,R * R.tranpose() 近似为一个单位矩阵。
void test4()
{Eigen::Matrix3d R;R << 0.74, 0.08, 0.25,0.2, 0.575, 0.05,0.17, 0.19, 0.675;Pose p1(R);Pose p2(p1.quaternion()); // Pose中,针对从四元数构造,默认有归一化功能R = p2.rotation();cout << "R = " << endl;cout << R << endl;cout << endl;cout << "R.inverse = " << endl;cout << R.inverse() << endl;cout << endl;cout << "R.transpose = " << endl;cout << R.transpose() << endl;cout << endl;cout << "R * R.transpose() = " << endl;cout << R * R.transpose() << endl;cout << endl;
}运行结果:
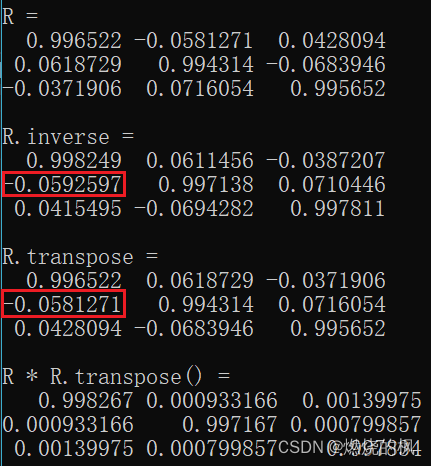
其中,R表示旋转,用旋转向量来描述(欧拉角有周期性和方向锁的问题,四元数有单位向量的约束,旋转矩阵冗余度太高且有各个基需要是单位正交的约束);t表示平移,用平移向量来描述。R和t均采用无约束的向量进行描述,于是也均可以通过网络的学习来得到。因为R和t共有六个自由度,因此姿态估计又称为6D姿态估计。
注:旋转向量的方向代表旋转轴,模长代表旋转角的大小,旋转方向为逆时针。
Eigen对于 translate 与 pretranslate的区别?(先平移、再旋转和 先旋转、再平移,有何区别?)可以看看这个:https://zhuanlan.zhihu.com/p/165020637
相关文章:

基于Eigen的位姿转换
位姿中姿态的表示形式有很多种,比如:旋转矩阵、四元数、欧拉角、旋转向量等等。这里基于Eigen实现四种数学形式的相互转换功能。本文利用Eigen实现上述四种形式的相互转换。我这里给出一个SE3(4*4)(先平移、再旋转)的构建方法&…...

Jmeter之Bean shell使用详解
一、什么是Bean Shell BeanShell是一种完全符合Java语法规范的脚本语言,并且又拥有自己的一些语法和方法;BeanShell是一种松散类型的脚本语言(这点和JS类似); BeanShell是用Java写成的,一个小型的、免费的、可以下载的、嵌入式的Java源代码解释器,具有对象脚本语言特性,非常精…...

TCP/IP(八)TCP的连接管理(五)四次握手
一 tcp连接断开 每一个TCP报文的超时重传都由一个特定的内核参数来控制 ① 四次握手的过程 遗留: 谁先发送FIN包,一定是client吗? --> upload和download补充: 主动和被动断开连接的场景 "四次握手过程描述" F --> FIN --> F…...

MyBatis-Plus主键生成策略[MyBatis-Plus系列] - 第491篇
历史文章(文章累计490) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 …...

Spring——和IoC相关的特性
目录 IoC中Bean的生命周期 实例化(Instantiation) 属性注入(Populate Properties) 初始化(Initialization) 使用(Bean in Use) 销毁(Destruction) Laz…...

在 TensorFlow 中调试
如果调试是消除软件错误的过程,那么编程一定是添加错误的过程。Edsger Dijkstra。来自 https://www.azquotes.com/quote/561997 一、说明 在这篇文章中,我想谈谈 TensorFlow 中的调试。 在之前的一些帖子(此处、此处和此处)中&…...

想要精通算法和SQL的成长之路 - 连续的子数组和
想要精通算法和SQL的成长之路 - 连续的子数组和 前言一. 连续的子数组和1.1 最原始的前缀和1.2 前缀和 哈希表 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 连续的子数组和 原题链接 1.1 最原始的前缀和 如果这道题目,用前缀和来算,我们的思路…...
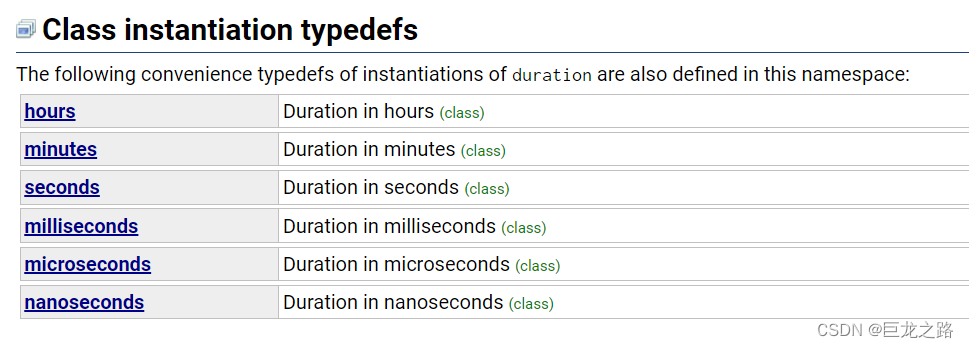
【C++】头文件chrono
2023年10月16日,周一晚上 当前我只是简单的了解了一下chrono 以后可能会深入了解chrono并更新文章 目录 功能原理头文件chrono中的一些类头文件chrono中的数据类型一个简单的示例程序小实验:证明a的效率比a高 功能 这个chrono头文件是用来处理时间的…...

Python学习六
前言:相信看到这篇文章的小伙伴都或多或少有一些编程基础,懂得一些linux的基本命令了吧,本篇文章将带领大家服务器如何部署一个使用django框架开发的一个网站进行云服务器端的部署。 文章使用到的的工具 Python:一种编程语言&…...

Springboot 集成 WebSocket
WebSocket是一种在单个TCP连接上进行全双工通信的协议。WebSocket使得客户端和服务器之间的数据交换变得更加简单,允许服务端主动向客户端推送数据。在WebSocket API中,浏览器和服务器只需要完成一次握手,两者之间就直接可以创建持久性的连接…...
谨以此篇,纪念我2023年曲折的计算机保研之路
目录 阶段一:迷茫阶段二:准备个人意愿保研材料准备套磁老师5.1日 浙大线上编程测试5.8日 浙大线上面试 —— 一面5.17日 浙大线上面试——二面5.29日 实验室面试结果5.27日 南开线上面试6.20日 华师电话面试 阶段三:旅途北航CS(6.…...
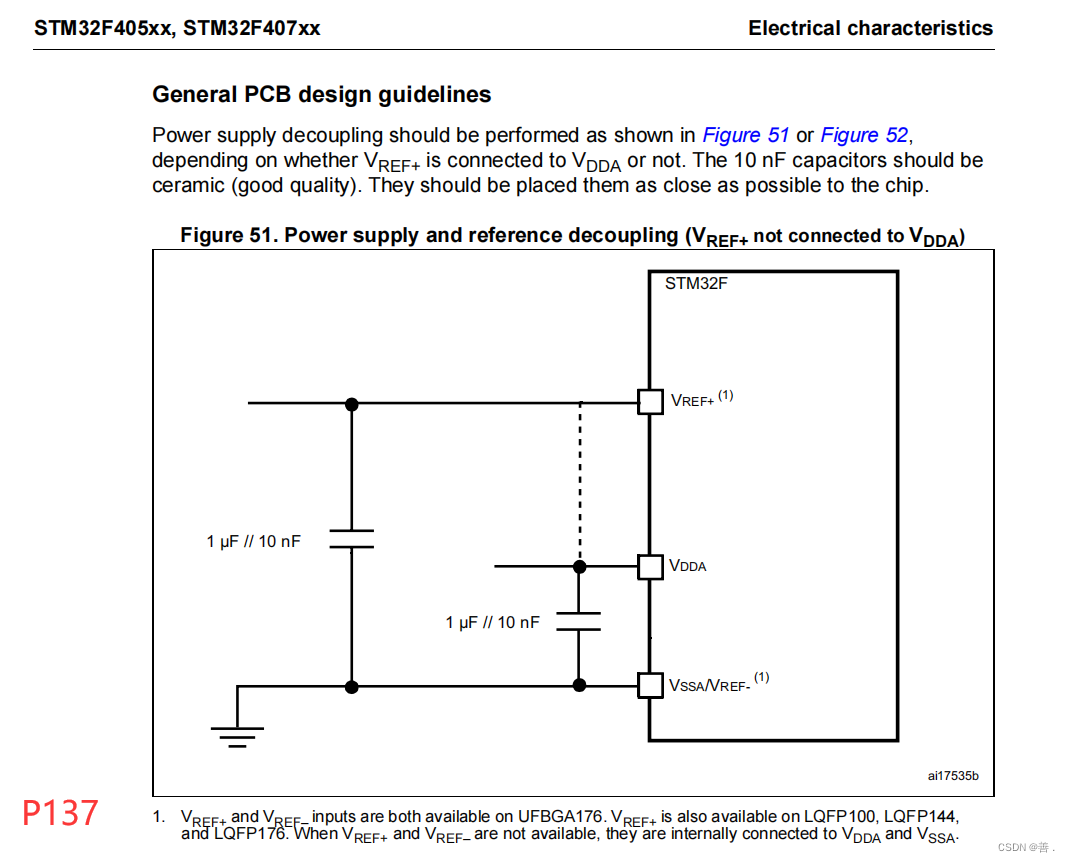
VSS、VDD、VBAT、VSSA
引言 在学习设计TM32时,发现芯片除了GPIO引脚外还会引出许多引脚,以STM32F407ZGT6为例除了GPIO引脚还会有以下引脚 如VSS、VDD、VBAT、VSSA、NRST、VREF、VDDA、VCAP_1、VCAP_2、PDR_ON这些引脚。他们有何作用,电路设计中应如何连接&#x…...

【Rust基础③】方法method、泛型与特征
文章目录 6 方法 Method6.1 定义方法self、&self 和 &mut self 6.2 自动引用和解引用6.3 关联函数 7 泛型和特征7.1 泛型 Generics7.1.1 结构体中使用泛型7.1.2 枚举中使用泛型7.1.3 方法中使用泛型为具体的泛型类型实现方法 7.1.4 const 泛型 7.2 特征 Trait7.2.1 为类…...
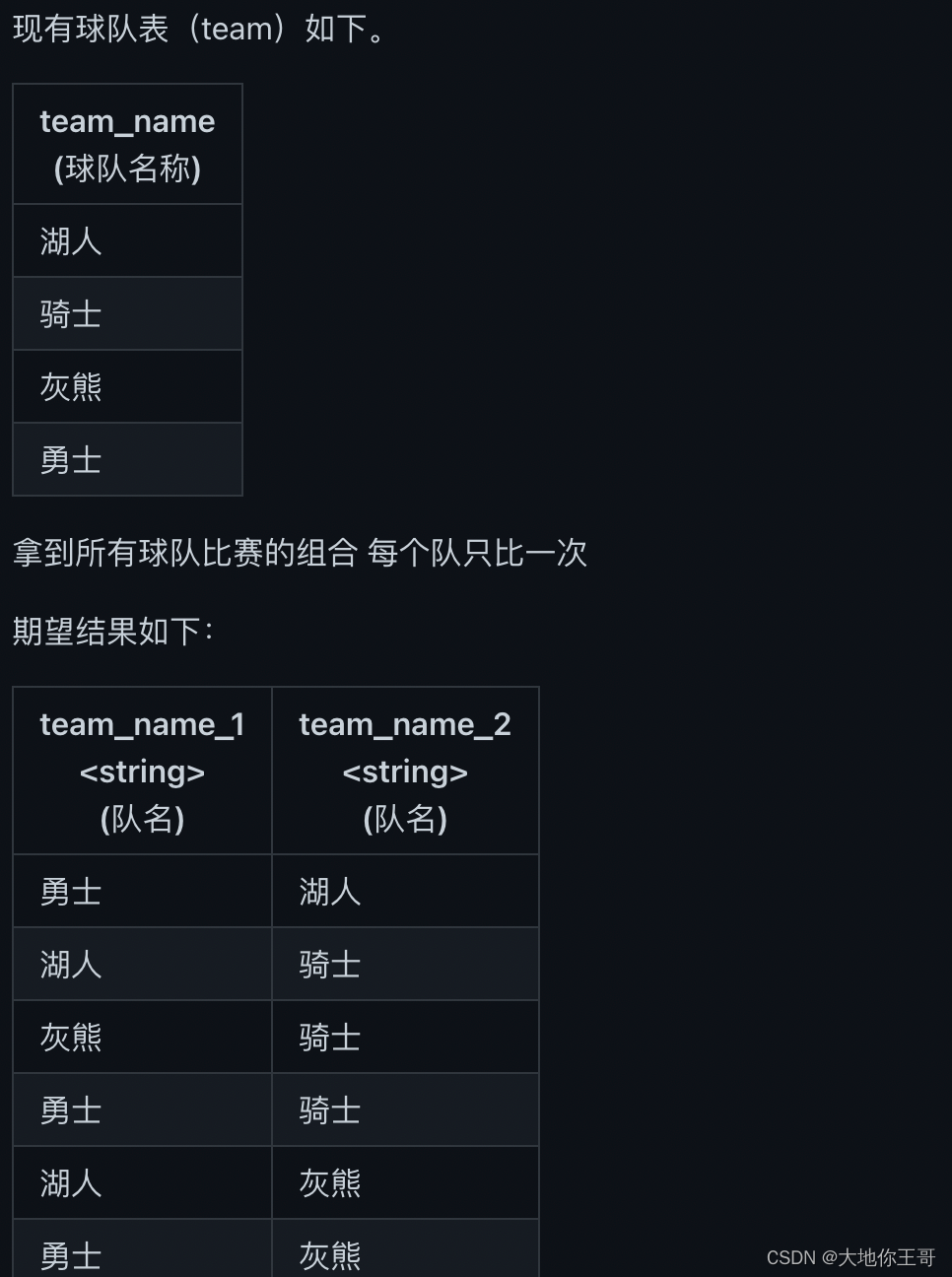
48.排列问题求解
思路分析:通过为每一队分配一个id,join条件要求t1.num < t2.num实现相同两队只比一次 代码实现: with t as (SELECT team_name,caseteam_nameWHEN 勇士 then 1WHEN 湖人 then 2WHEN 灰熊 then 3else 4end numFROM team )SELECT t1.team_…...

18.(开发工具篇Gitlab)Git如何回退到指定版本
首先: 使用git log命令查看提交历史,找到想要回退的版本的commit id. 使用git reset命令 第一步:git reset --hard 命令是强制回到某一个版本。执行后本地工程回退到该版本。 第二步:利用git push -f命令强制推到远程 如下所示: 优点:干净利落,回滚后完全回到最初状态…...
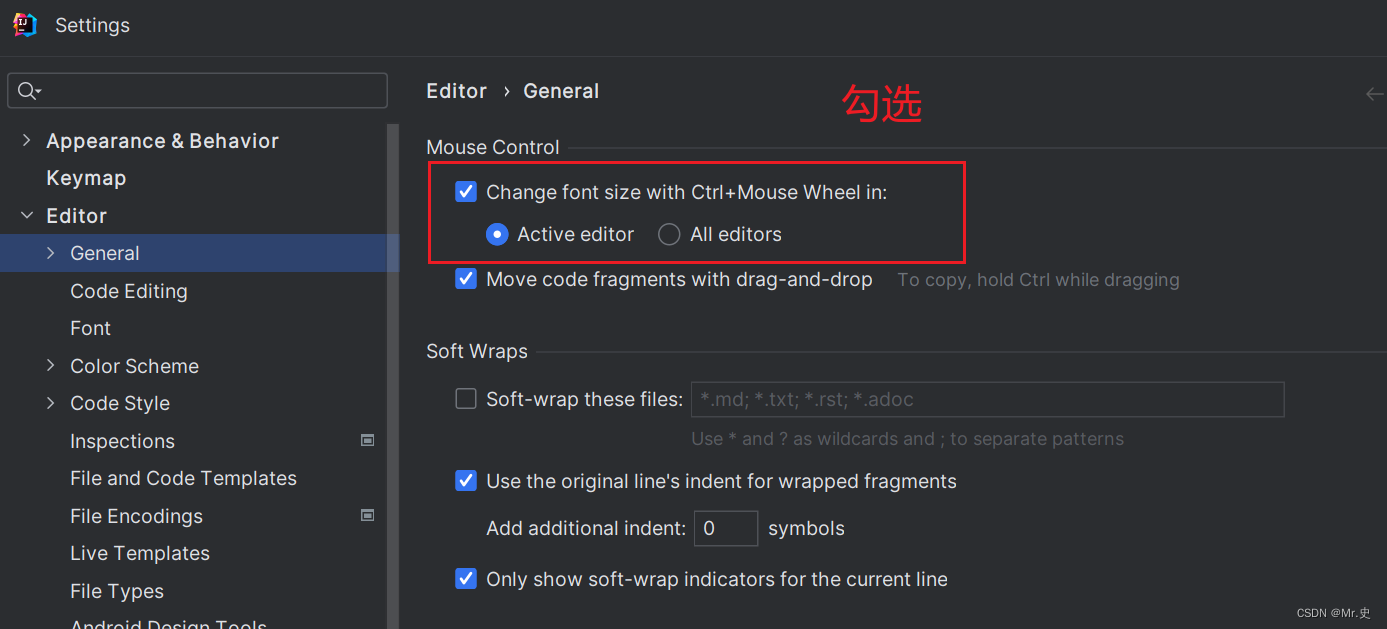
IDEA初始配置
1. 详细设置 安装完IDEA之后的简单配置。 1.1 如何打开详细配置界面 1、显示工具栏 2、选择详细配置菜单或按钮 1.2 系统设置 1、默认启动项目配置 启动IDEA时,默认自动打开上次开发的项目?还是自己选择? 如果去掉Reopen projects on …...

WM_COPYDATA传回返回值的一个方案
方案背景 适应场景,通过WM_COPYDATA进行进程间通信时,SendMessage不能返回自定义的数据,由此想到以下思路解决这个问题 A进程使用VirtualAlloc分配一块内存,通过某种方式将此地址以及A进程ID传给另一个进程B B进程使用OpenProce…...
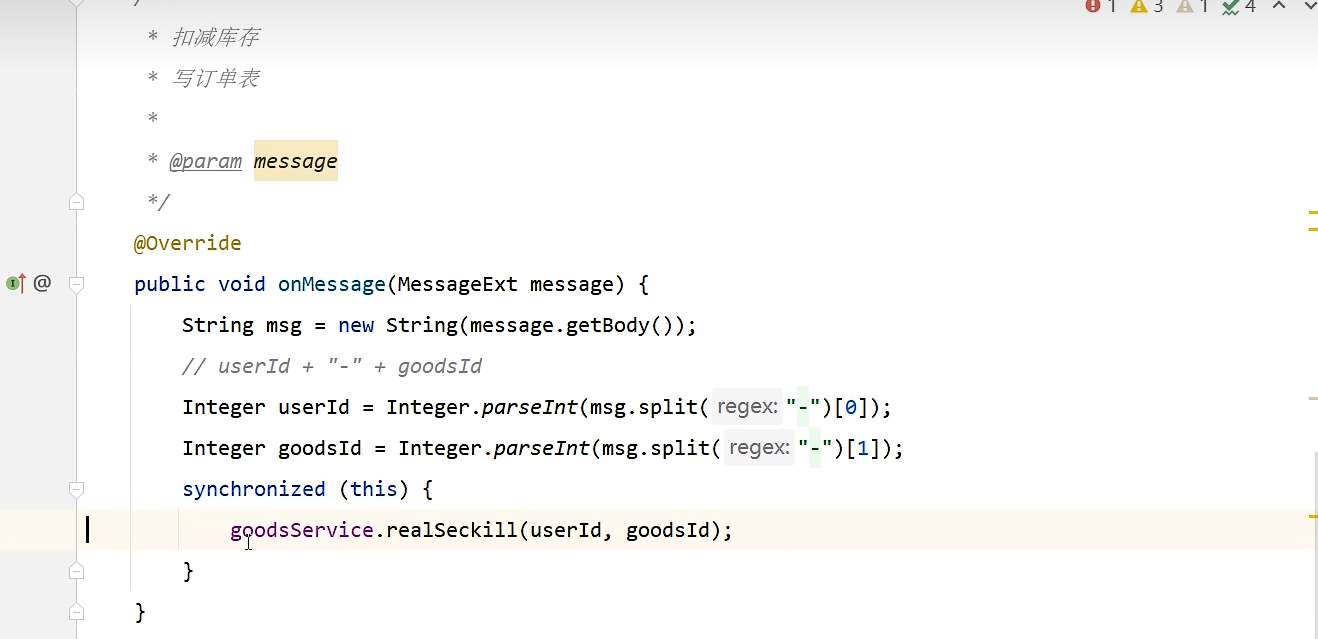
【日常业务开发】接口性能优化
【日常业务开发】接口性能优化 缓存本地缓存分布式缓存 数据库分库分表SQL 优化 业务程序并行化异步化池化技术预先计算事务粒度批量读写锁的粒度尽快return上下文传递空间换时间集合空间大小 缓存 本地缓存 本地缓存,最大的优点是应用和cache同一个进程内部&…...
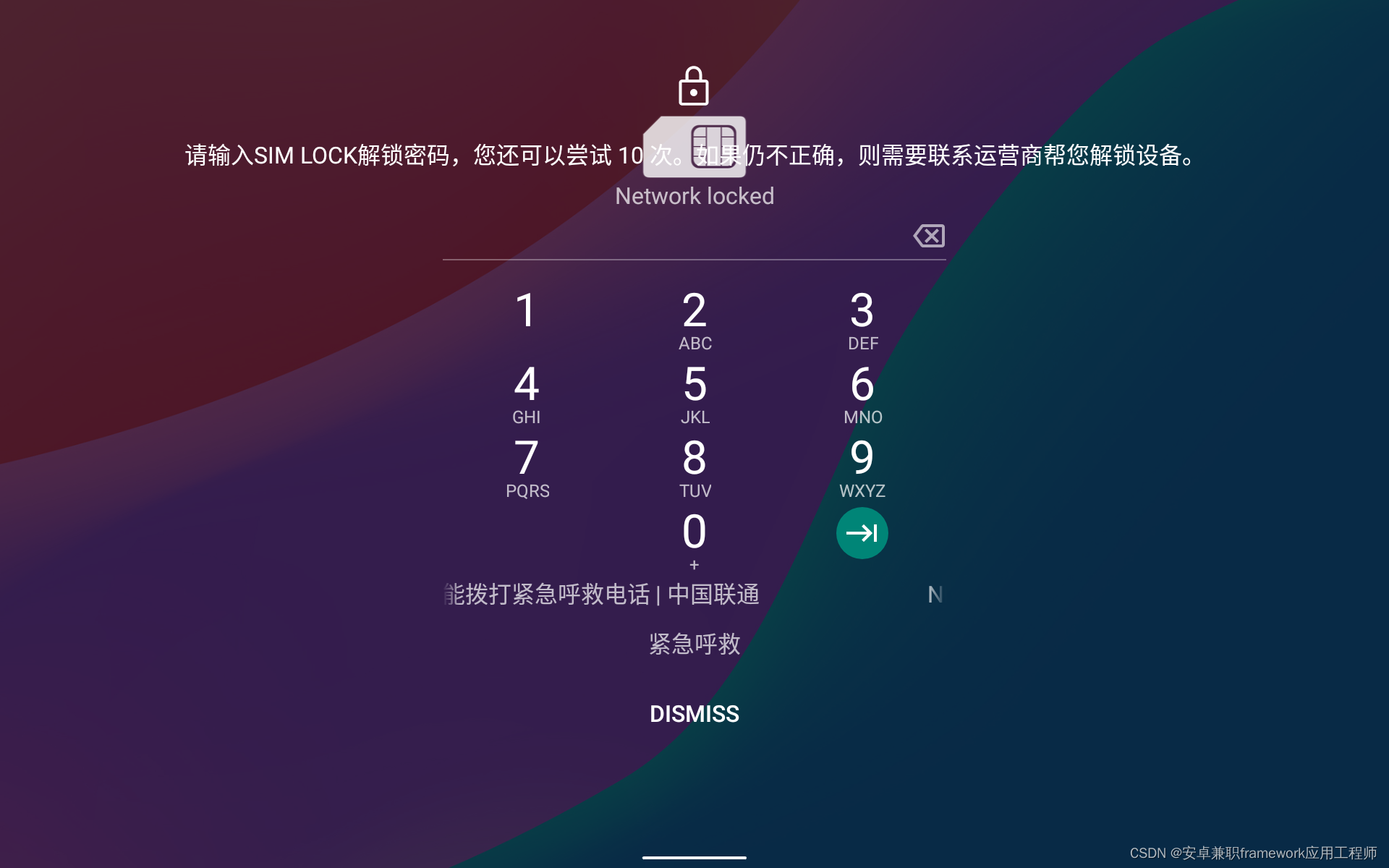
Android 10.0 禁止弹出系统simlock的锁卡弹窗功能实现
1.前言 在10.0的系统开发中,在一款产品中,需要实现simlock锁卡功能,在系统实现锁卡功能以后,在开机的过程中,或者是在插入sim卡 后,当系统检测到是禁用的sim卡后,就会弹出simlock锁卡弹窗,要求输入puk 解锁密码,功能需求禁用这个弹窗,所以就需要看是 哪里弹的,禁用…...
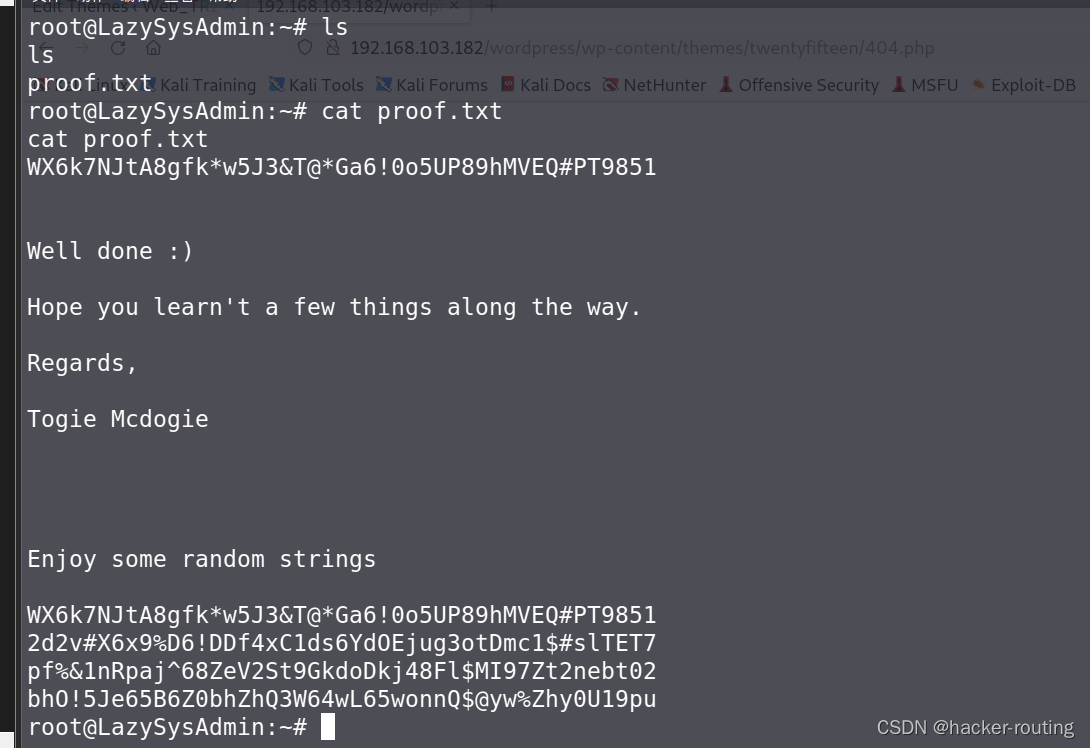
VulnHub lazysysadmin
一、信息收集 1.nmap扫描开发端口 开放了:22、80、445 访问80端口,没有发现什么有价值的信息 2.扫描共享文件 enum4linux--扫描共享文件 使用: enum4linux 192.168.103.182windows访问共享文件 \\192.168.103.182\文件夹名称信息收集&…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
