[牛客习题]“幸运的袋子”
习题链接:幸运的袋子_牛客题霸_牛客网
题目分析
由题意可知:“幸运的袋子”的概念是——小球的数值之和大于小球的数值之积。
假如现在有5个小球:1,1,3,5,7,并将他们编号a0~a4.我们现在来看其中一种满足“幸运”条件的情况:我们设置变量sum来记录数值之和,用multi来记录数值之积,用count来记录袋子数量。
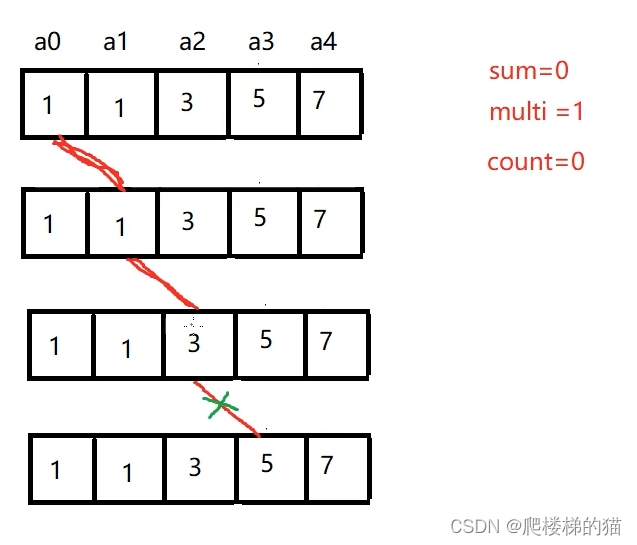
我们先取a0这个小球,数值为1。接着取a1——(1+1)>(1*1),满足条件,计数器count+1.我们继续取a2——(1+1+3)>(1*1*3),满足条件,计数器count+1.
接着我们取a3,(1+1+3+5+7)<(1*1*3*5*7),不满足条件。那么我们就要回到上一层(取a2的那一层)来试试下一个取a4是否满足要求。
但是此时sum = (1+1+3+5+7) = 17,multi = 105,要想回到上一层就得sum减去刚拿到的a3,multi除以刚乘上的a3.然后去取a4,看看是否满足条件。
但是因为我们对数字进行递增排序了,如果a3不满足条件,那么a4也不会满足。
最后返回count的值。
如果我们写一个count函数,用来获得从取得某个球开始的“幸运袋子”的个数。对于n个小球来说,自小球a0开始的袋子个数为:小球a0与下一个小球ax之间袋子的个数 加上 以小球ax开始与ax的下一个小球之间的袋子个数 之和。然后依次递归
那么回到一个小球也没取的时候,此时为空(什么也没有),那么袋子的个数是不是 取第一个小球的个数(此时你取哪个小球都满足要求,因为此时就一个小球)加上 第一个小球与其取得下一个小球所有可能?
很好,现在我们总结出了其中的规律,现在我们来写代码
import java.util.*;
public class FortunatePackage {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();//输入小球的个数int[] a = new int[n];//将所有小球放入一个数组中,以数组下标为小球编号for (int i = 0; i < n; i++) {a[i] = sc.nextInt();}Arrays.sort(a);//将小球递增排序,以节省算力/*为什么要排序?仍然以(1,1,3,5,7)为例,当取到5时,5不满足要求,那么它后面的数都比它大,也一定不满足要求了*/System.out.println(count(a, n, 0, 0, 1));//从第一个下标开始取小球}/*pos是查找“幸运袋子”时的“第一个球的位置”,a[]是目前可供挑选的球,sum为和(初始值为0),multi为积(初始值为1),n为球的个数*/public static int count(int[] a,int n,int pos,int sum,int multi){int count = 0;for (int i = pos; i < n; i++) {sum += a[i];multi *= a[i];//如果这两个球满足“幸运袋子”的要求,“幸运袋子”的组合种类数为 1(这两个球组成的袋子)+ 剩下的所有球中存在的“幸运袋子”数if (sum > multi){count = count + 1 + count(a,n,i+1,sum,multi);}else if (a[i] == 1){count = count + count(a,n,i+1,sum,multi);}else {break;}//如果这两个球不满足“幸运袋子”的要求,则清除此次操作带来的数据改变,回溯到上一层sum -= a[i];multi /= a[i];//如果这个球不满足要求并且和下一个球的数值相等,则跳过下一个球的检测while (i < n-1 && a[i] == a[i+1]){i++;}}return count;}
}
相关文章:

[牛客习题]“幸运的袋子”
习题链接:幸运的袋子_牛客题霸_牛客网 题目分析 由题意可知:“幸运的袋子”的概念是——小球的数值之和大于小球的数值之积。 假如现在有5个小球:1,1,3,5,7,并将他们编号a0~a4.我们…...
安科瑞预付费系统在某大型连锁农贸市场的设计应用
安科瑞 崔丽洁 摘要 本远程预付费管理系统采用智能远程预付费电表(DTSY1352-NK/DDSY1352-NK系列),NB智能远传水表,采集各商户实时用电量、用电量总数,通过平台定时结算,结算账户余额,从而进行智…...
Spring Boot Bean 注入的常用方式教程
Spring Boot Bean 注入是一种将依赖对象引入到应用程序组件中的机制,它有助于实现松耦合和可测试的代码。这种注入方式允许我们将依赖关系委托给 Spring 容器来管理,从而提高了代码的可维护性和可读性。Spring Boot 提供了多种 Bean 注入方式,…...
Java项目调用Python脚本(基于idea)
前期准备 1.首先需要在本地环境中安装配置python环境 Python(含PyCharm及配置)下载安装以及简单使用(Idea) 博主本次使用python版本为py3.7.3 2.idea安装python插件 位置:File->Settings->Plugins->python->安装后重启即可 3.引入jython依赖 &l…...

前端 JS 经典:i,i++,++i区别
1. 概念 用于对变量进行自增操作。它们的区别在于返回值不同。 i 表示先使用 i 的值,再将 i 加 1,返回的是 i 自增前的值。 i 表示先将 i 加 1,再使用 i 的值,返回的是 i 自增后的值。 i 表示直接使用 i 的值,不进…...

EF Core 7.0 新特性之批量修改
概要 EF Core 7.0 提供了一个可以将LINQ查询和批量修改相结合的方法ExecuteUpdate。由于数据修改是以批量更新的方式完成,所以可以减少数据库的往返次数。 本文将主要介绍ExecuteUpdate的使用方法。 代码和实现 基本案例 本文我们使用银行分行,ATM机…...

Vue_Bug error0308010Cdigital envelope routinesunsupported
Bug描述: error0308010Cdigital envelope routinesunsupported 解决方法: Just add this to the top of vue.config.js : const crypto require(crypto);/*** md4 algorithm is not available anymore in NodeJS 17 (because of lib SSL 3).* In that…...

中科院提出“思维传播”,极大增强ChatGPT等模型复杂推理能力
中国科学院自动化研究所与耶鲁大学计算机系研究人员联合发布了,一份名为《思维传播:用大型语言模型进行基于类比的复杂推理》的论文。 ChatGPT等大型语言模型展示出了超强的创造能力,只需简单的文本提示就能生成小说、营销创意、简历等各种文本内容。但…...

ubuntu20.04安装opencv 3.2.0 报错
安装记录 Error 1: cmake时报错 CMake Error at cmake/OpenCVCompilerOptions.cmake:21 (else): A duplicate ELSE command was found inside an IF block. Fix: 修改opencv-3.2.0/cmake/OpenCVCompilerOptions.cmake文件 注释掉21和22行 else()message(STATUS "Unabl…...
KubeVela交付
有什么用我也不想说了,这个是k8s CI/CD,进阶玩家玩的了,比你们喜欢Arg CD更科学,更现代 在 Kubernetes 中安装 KubeVela helm repo add kubevela https://charts.kubevela.net/core helm repo update helm install --create-namespace -n v…...

【SpringCloud-10】SCA-nacos
前言: 前面介绍的springcloud,可以看做第一代,称为:SCN(spring cloud Netflix); 接下来介绍的是第二代:SCA(spring cloud alibaba); SCA主要有以下组件&#…...

卡顿分析与布局优化
卡顿分析与布局优化 大多数用户感知到的卡顿等性能问题的最主要根源都是因为渲染性能。Android系统每隔大概16.6ms发出VSYNC信 号,触发对UI进行渲染,如果每次渲染都成功,这样就能够达到流畅的画面所需要的60fps,为了能够实现60fp…...
【Vivado HLS Bug】Ubuntu环境下Vivado HLS导出IP报错:HLS ERROR: [IMPL 213-28]
Export IP Invalid Argument / Revision Number Overflow Issue (Y2K22) (xilinx.com)一.问题描述: 在Ubuntu20.04环境中使用Vivado HLS导出IP时报错:HLS ERROR: [IMPL 213-28] 二.解决方法: 1.从如下链接中下载官方补丁Export IP Invalid…...

2022最新版-李宏毅机器学习深度学习课程-P14 批次(batch)与动量(momentum)
一、batch 回顾epoch、shuffle batch size大还是小?都有好处 大batchsize的好处 由于GPU有并行计算的能力,左边并不一定用时更长 反而是,batch size小的时候,要跑完一个epoch所用的update时间更长,所以时间方面的比较…...

谜题(Puzzle, ACM/ICPC World Finals 1993, UVa227)rust解法
有一个5*5的网格,其中恰好有一个格子是空的,其他格子各有一个字母。一共有4种指令:A, B, L, R,分别表示把空格上、下、左、右的相邻字母移到空格中。输入初始网格和指令序列(以数字0结束),输出指…...

acwing算法基础之数据结构--双链表
目录 1 知识点2 模板 1 知识点 一般的结构体写法为, struct BiListNode {int val;BiListNode *left;BiListNode *right; };但我们不用这个,而用数组模拟双链表,此时,用编号为0的结点表示头结点,用编号为1的结点表示尾…...
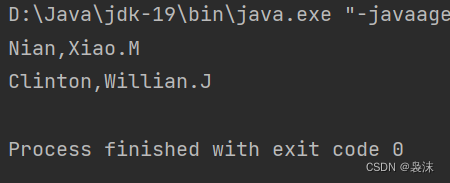
将中文名格式化输出为英文名
要求: 编写Java程序,输入样式为:Zhong wen ming的人名,以 Ming,Zhong.W 的形式打印出来。其中.W是中间单词的首字母;例如输入”Willian Jefferson Clinton“,输出形式为:Clinton,Willian.J public static …...
设计模式_迭代器模式
迭代器模式 介绍 设计模式定义案例迭代器模式行为型:关注对象与行为的分离 提供了一种统一的方式来访问多个不同的集合两个集合:使用了不同的数据存储方式 学生 和 警察 查询显示出集合的内容 ,使用相同的代码 问题堆积在哪里解决办法不同…...
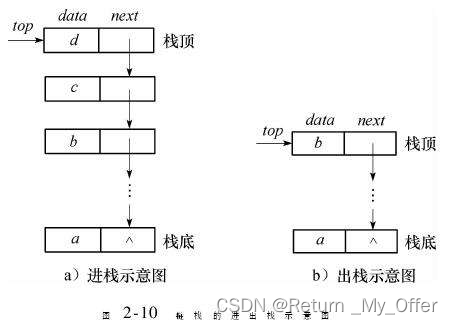
【数据结构】:栈的实现
1 栈 1.1栈的概念及结构 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则 压栈…...

微前端一:技术选型
微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略。 微前端架构具备以下几个核心价值: 1、技术栈无关 主框架不限制接入应用的技术栈,微应用具备完全自主权 2、独立开发、独立部署 微应用仓库独立࿰…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
