算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯
算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯
理论基础
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,
规是由前一个状态推导出来的,而贪心是局部直接选最优的,
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
斐波那契数
509. 斐波那契数 - 力扣(LeetCode)
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。
这里我们要用一个一维dp数组来保存递归的结果
-
确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
-
确定递推公式
题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
-
dp数组如何初始化
题目中把如何初始化也直接给我们了
-
确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
-
举例推导dp数组
class Solution {public int fib(int n) {if(n<=1) return n;int[] dp = new int[n+1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <=n; i++) {dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}
爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
动规五部曲:
定义一个一维数组来记录不同楼层的状态
-
确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
-
确定递推公式
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
-
dp数组如何初始化
其实这么争论下去没有意义,大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1。
所以我的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
-
确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
-
举例推导dp数组
class Solution {public int climbStairs(int n) {if (n<2) return n;int[] dp = new int[n+1];dp[1] = 1;dp[2] = 2;for (int i = 3; i < dp.length ; i++) {dp[i] = dp[i-2]+dp[i-1];}return dp[n];}
}
使用最小花费爬楼梯
746. 使用最小花费爬楼梯 - 力扣(LeetCode)
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
-
确定dp数组以及下标的含义
本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
2. 确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
-
dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
-
确定遍历顺序
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
-
举例推导dp数组
class Solution {public int minCostClimbingStairs(int[] cost) {if (cost.length==0) return 0;if (cost.length==1) return cost[0];int[] dp = new int[cost.length+1];dp[0] = 0;dp[1] = 0;for (int i = 2; i < dp.length; i++) {dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.length];}
}
相关文章:

算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯
算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯 理论基础 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 所以动态规划中每一个状…...

MySQL8 创建用户,设置修改密码,授权
MySQL8 创建用户,设置修改密码,授权 MySQL5.7可以 (创建用户,设置密码,授权) 一步到位 👇 GRANT ALL PRIVILEGES ON *.* TO 用户名% IDENTIFIED BY 密码 WITH GRANT OPTION👆这样的语句在MySQL8.0中行不通, 必须 创设和授权 分步执行👇 CR…...

MySQL —— 内置函数
目录 内置函数 一、日期函数 二、字符串函数 三、数学函数 四、其他函数 内置函数 一、日期函数 函数名称描述current_date()获取当前日期current_time()获取当前时间current_timestamp()获取当前时间戳now()获取当前日期时间date(datetime)获取datetime参数的日期部分d…...

Mybatis框架(全部基础知识)
👌 棒棒有言:也许我一直照着别人的方向飞,可是这次,我想要用我的方式飞翔一次!人生,既要淡,又要有味。凡事不必太在意,一切随缘,缘深多聚聚,缘浅随它去。凡事…...

pixhawk2.4.8使用调试记录—APM固件
目录一、硬件准备二、APM固件、MP地面站下载三、地面站配置1 刷固件2 机架选择3 加速度计校准4 指南针校准5 遥控器校准6 飞行模式7 紧急断电&无头模式8 基础参数设置9 电流计校准10 电调校准11 起飞前检查(每一项都非常重要)12 飞行经验四、遇到的问…...
终于进了字节,记录一下我作为一名测试员磕磕碰碰的三个月找工作经历...
我是裸辞后重新找工作的,从去年到今年,前前后后花了大概三个月,大大小小参加了几百场面试。不是我说,作为一名测试员是真的挺难的,不过很庆幸自己最后拿到了字节的offer,今天在这里做一下记录吧,…...

基于PYTHON django四川旅游景点推荐系统
摘 要基于四川旅游景点推荐系统的设计与实现是一个专为四川旅游景点为用户打造的旅游网站。该课题基于网站比较流行的Python 语言系统架构,B/S三层结构模式,通过Maven项目管理工具进行Jar包版本的控制。本系统用户可以发布个人游记,查看景点使用户达到良…...

MySql服务多版本之间的切换
从网上总结的经验,然后根据自己所遇到的问题合并记录一下,方便日后再次需要用到 MySql服务多版本同时运行 步骤 1、如果你电脑上已经有一个mysql版本,例如mysql-5.7.39-winx64,它占据了3306端口。此时如果你想下仔另一版本&…...

嵌入式开发:通过嵌入式虚
嵌入式虚拟化为实现多核处理能力的优势提供了一种可扩展的机制。嵌入式应用中的虚拟化与其企业和桌面应用有许多共同之处。独特的嵌入式使用案例和专业的底层技术为嵌入式开发人员提供了优化性能和响应设计的新机会。在台式机、数据中心以及现在的嵌入式设计中采用多核技术可以…...

广州穗雅医院杨济安:了解症状表现 有效防治口腔黏膜下纤维化
“医生,我出现口干大半年时间,最近两月张嘴费劲,吃点辣的,嘴就刺疼刺疼的,这是怎么回事?”半年前,家住南沙的文先生走进广州穗雅医院口腔黏膜科如是说到。在科室杨济安主任的详细问诊与检查后&a…...
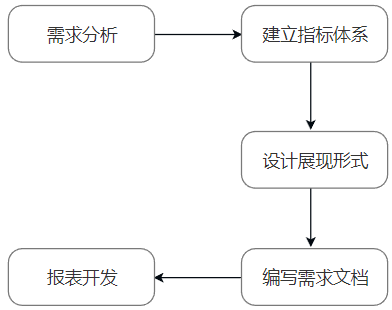
[数据分析] 数据指标体系搭建
在数据分析的学习过程中,我们通常会要求掌握以下两点: 1.理解数据,懂得从数据中发现业务指标(学会如何去看懂数据) 2.使用相关指标去分析数据,同时使用多个指标去分析一个问题(了解常见的指标) 当我们拿到数据(通常以Excel或者数据库方式去…...

Dubbo 源码分析 – 集群容错之 Cluster
3.2.2 FailbackClusterInvoker FailbackClusterInvoker 会在调用失败后,返回一个空结果给服务提供者。并通过定时任务对失败的调用进行重传,适合执行消息通知等操作。下面来看一下它的实现逻辑。 public class FailbackClusterInvoker<T> extend…...

Spring学习20230208-09
IOC底层原理 IOC概念 :面向对象编程中的一种设计原则,用来降低耦合度 通过控制反转,对象在被创建的时候,由一个调控系统内所有对象的外界实体将其所依赖的对象引用传递给他。可以说,依赖被注入到对象中。控制反转&…...
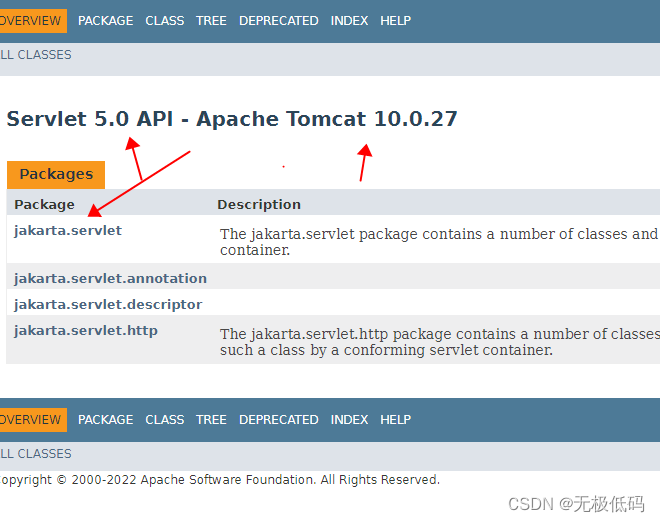
tomcat10部署报错WebStatFilter cannot be cast to jakarta.servlet.Filter
异常信息09-Feb-2023 23:08:49.946 严重 [main] org.apache.catalina.core.StandardContext.filterStart 启动过滤器异常[DruidWebStatFilter]java.lang.ClassCastException: com.alibaba.druid.support.http.WebStatFilter cannot be cast to jakarta.servlet.Filterat org.ap…...
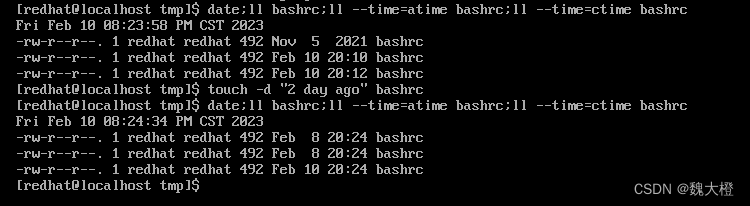
Linux修改文件时间或创建新文件:touch
每个文件在Linux下面都记录了许多的时间参数,其实是三个主要的变动时间 修改时间(modification time,mtime):当该文件的【内容数据】变更时,就会更新这个时间,内容数据是指文件的内容ÿ…...

原生微信小程序按需引入vant
vant Vant Weapp - 轻量、可靠的小程序 UI 组件库 1.npm安装 找到项目根目录 安装 # 通过 npm 安装 npm i vant/weapp -S --production# 通过 yarn 安装 yarn add vant/weapp --production# 安装 0.x 版本 npm i vant-weapp -S --production 2 .修改 app.json 将 app.jso…...
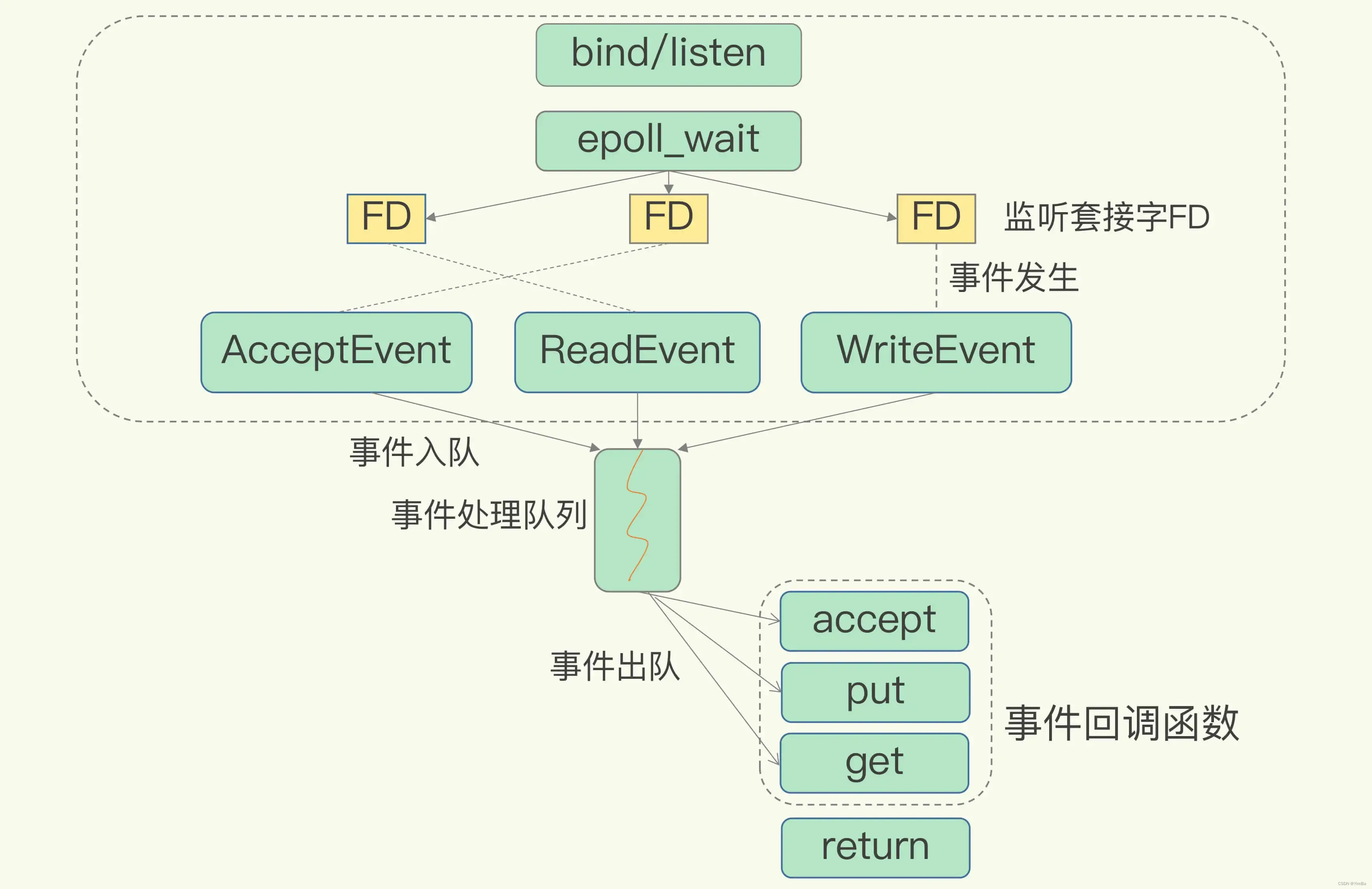
高性能IO模型:为什么单线程Redis能那么快?
我们通常说Redis是单线程,主要是指Redis的网络IO和键值对读写是由一个线程来完成的。这也是Redis对外提供键值存储服务的主要流程。 但redis的其他功能,比如持久化、异步删除、集群数据同步等,其实是由额外的线程执行的。 Redis为什么用单线…...

【数据集】中国各类水文专业常用数据集合集
1 水文气象数据 1.1 中国站点尺度天然径流量估算数据集(1961~2018年) 论文: J2022-High-quality reconstruction of China’s natural streamflow-缪驰远(北京师范大学地理科学学部) 研究内容:…...
落枕、肩颈酸痛,用磁疗就可缓解!
睡觉之前还是好好的,一觉醒来脖子莫名疼痛,转都转不了,有时候连肩膀和上肢都难受,很可能是“落枕”了。 落枕引起的肩颈疼痛与多种因素有关,如颈肩部肌肉的过度使用、不良的睡眠姿势或颈肩部受寒湿空气的侵袭ÿ…...

一文教会你如何选择远程桌面(五大主流远程软件全面讲解)
写在前面 作为程序员的我们,随时随地写代码改代码是我们的日常。刚回到家,就被老板、产品经理cue是常有的事。基于这种情况,一般都会随身携带电脑,随时备战,不过每天背着电脑上下班非常不方便。因此资深程序员的解决方…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
