[论文精读]Semi-Supervised Classification with Graph Convolutional Networks
论文原文:[1609.02907] Semi-Supervised Classification with Graph Convolutional Networks (arxiv.org)
论文代码:GitHub - tkipf/gcn: Implementation of Graph Convolutional Networks in TensorFlow
英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用!
1. 省流版
1.1. 心得
(1)怎么开头我就不知道在说什么啊这个论文感觉表述不是很清晰?
(2)数学部分推理很清晰
1.2. 论文框架图
2. 论文逐段阅读
2.1. Abstract
①Their convolution is based on localized first-order approximation
②They encode node features and local graph structure in hidden layers
2.2. Introduction
①The authors think adopting Laplacian regularization in the loss function helps to label:
where represents supervised loss with labeled data,
is a differentiable function,
denotes weight,
denotes matrix with combination of node feature vectors,
represents the unnormalized graph Laplacian,
is adjacency matrix,
is degree matrix.
②The model trains labeled nodes and is able to learn labeled and unlabeled nodes
③GCN achieves higher accuracy and efficiency than others
2.3. Fast approximate convolutions on graphs
①GCN (undirected graph):
where denotes autoregressive adjacency matrix, which means
,
denotes identity matrix,
denotes autoregressive degree matrix,
represents the trainable weight matrix in
-th layer,
denotes the activation matrix in
-th layer,
represents activation function
2.3.1. Spectral graph convolutions
①Spectral convolutions on graphs:
where the filter ,
comes from normalized graph Laplacian
and is the matrix of
's eigenvectors,
denotes a diagonal matrix with eigenvalues.
②However, it is too time-consuming to compute matrix especially for large graph. Ergo, approximating it in -th order by Chebyshev polynomials:
where ,
denotes Chebyshev coefficients vector,
recursive Chebyshev polynomials are with baseline
and
③Then get new function:
where ,
.
④Through this approximation method, time complexity reduced from to
2.3.2. Layer-wise linear model
①Then, the authors stack the function above to build multiple conv layers and set ,
②They simplified 2.3.1. ③ to:
where and
are free parameters
③Nevertheless, more parameters bring more overfitting problem. It leads the authors change the expression to:
where they define ,
eigenvalues are in .
But keep using it may cause exploding/vanishing gradients or numerical instabilities.
④Then they adjust
⑤The convolved signal matrix :
where denotes input channels, namely feature dimensionality of each node,
denotes the number of filters or feature maps,
represents matrix of filter parameters
2.4. Semi-supervised node classification
2.4.1. Example
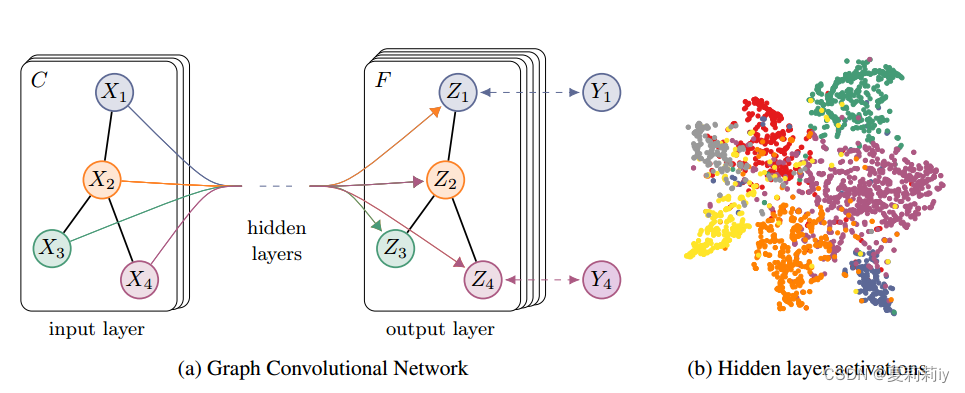
2.4.2. Implementation
2.5. Related work
2.5.1. Graph-based semi-supervised learning
2.5.2. Neural networks on graphs
2.6. Experiments
2.6.1. Datasets
2.6.2. Experimental set-up
2.6.3. Baselines
2.7. Results
2.7.1. Semi-supervised node classifiication
2.7.2. Evaluation of propagation model
2.7.3. Training time per epoch
2.8. Discussion
2.8.1. Semi-supervised model
2.8.2. Limitations and future work
2.9. Conclusion
3. 知识补充
4. Reference List
Kipf, T. & Welling, M. (2017) 'Semi-Supervised Classification with Graph Convolutional Networks', ICLR 2017, doi: https://doi.org/10.48550/arXiv.1609.02907
相关文章:

[论文精读]Semi-Supervised Classification with Graph Convolutional Networks
论文原文:[1609.02907] Semi-Supervised Classification with Graph Convolutional Networks (arxiv.org) 论文代码:GitHub - tkipf/gcn: Implementation of Graph Convolutional Networks in TensorFlow 英文是纯手打的!论文原文的summari…...

CICD:使用docker+ jenkins + gitlab搭建cicd服务
持续集成解决什么问题 提高软件质量效率迭代便捷部署快速交付、便于管理 持续集成(CI) 集成,就是一些孤立的事物或元素通过某种方式集中在一起,产生联系,从而构建一个有机整体的过程。 持续,就是指长期…...

新能源电池试验中准确模拟高空环境大气压力的解决方案
摘要:针对目前新能源电池热失控和特性研究以及生产中缺乏变环境压力准确模拟装置、错误控制方法造成环境压力控制极不稳定以及氢燃料电池中氢气所带来的易燃易爆问题,本文提出了相应的解决方案。方案的关键一是采用了低漏率电控针阀作为下游控制调节阀实…...

Python 中的模糊字符串匹配
文章目录 Python中使用thefuzz模块匹配模糊字符串使用process模块高效地使用模糊字符串匹配今天,我们将学习如何使用 thefuzz 库,它允许我们在 python 中进行模糊字符串匹配。 此外,我们将学习如何使用 process 模块,该模块允许我们借助模糊字符串逻辑有效地匹配或提取字符…...

记录一个奇怪bug
一开始Weapon脚本是继承Monobehavior的,实例化后挂在gameObject上跟着角色。后来改成了不继承mono的,也不实例化。过程都是顺利的,运行也没问题,脚本编辑器也没有错误。 但偶尔有一次报了一些错误,大概是说Weapon (1)…...

SpringBoot面试题7:SpringBoot支持什么前端模板?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:SpringBoot支持什么前端模板? Spring Boot支持多种前端模板,其中包括以下几种常用的: Thymeleaf:Thymeleaf是一种服务器端Java模板引擎,能够…...

leetcode做题笔记172. 阶乘后的零
给定一个整数 n ,返回 n! 结果中尾随零的数量。 提示 n! n * (n - 1) * (n - 2) * ... * 3 * 2 * 1 示例 1: 输入:n 3 输出:0 解释:3! 6 ,不含尾随 0示例 2: 输入:n 5 输出&a…...

linux之shell脚本练习
以下脚本已经是在ubuntu下测试的 demo持续更新中。。。 1、for 循环测试,,,Ping 局域网 #!/bin/bashi1 for i in {1..254} do# 每隔0.3s Ping 一次,每次超时时间3s,Ping的结果直接废弃ping-w 3 -i 0.3 192.168.110.$i…...
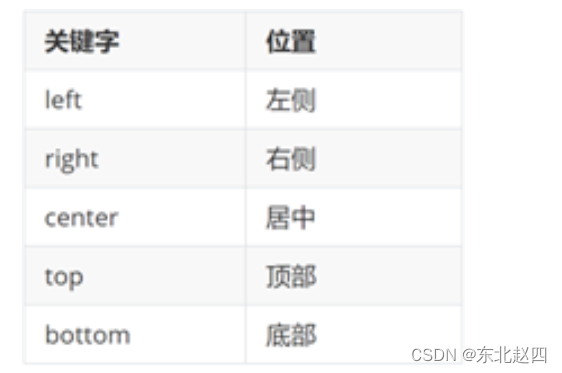
CSS阶详细解析一
CSS进阶 目标:掌握复合选择器作用和写法;使用background属性添加背景效果 01-复合选择器 定义:由两个或多个基础选择器,通过不同的方式组合而成。 作用:更准确、更高效的选择目标元素(标签)。…...

osWorkflow-1——osWorkflow官方例子部署启动运行(版本:OSWorkflow-2.8.0)
osWorkflow-1——osWorkflow官方例子部署启动运行(版本:OSWorkflow-2.8.0) 1. 前言——准备工作1.1 下载相关资料1.2 安装翻译插件 2. 开始搞项目2.1 解压 .zip文件2.2 简单小测(war包放入tomcat)2.3 导入项目到 IDE、…...

Stm32_标准库_13_串口蓝牙模块_手机与蓝牙模块通信
代码: #include "stm32f10x.h" // Device header #include "Delay.h" #include "OLED.h" #include "Serial.h"char News[100] "";uint8_t flag 1;void Get_Hc05News(char *a){uint32_t i 0…...
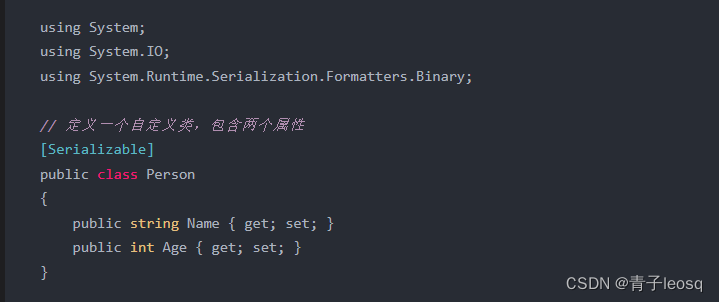
Unity中用序列化和反序列化来保存游戏进度
[System.Serializable]标记类 序列化 [System.Serializable]是一个C#语言中的属性,用于标记类,表示该类的实例可以被序列化和反序列化。序列化是指将对象转换为字节流的过程,以便可以将其保存到文件、数据库或通过网络传输。反序列化则是将字…...

Junit 单元测试之错误和异常处理
错误和异常处理是测试中非常重要的部分。假设我们有一个服务,该服务从数据库中获取用户。现在,我们要考虑的错误场景是:数据库连接断开。 整体代码示例 首先,为了简化,我们让服务层就是简单的类,然后使用I…...
LockSupport-park和unpark编码实战
package com.nanjing.gulimall.zhouyimo.test;import java.util.concurrent.TimeUnit; import java.util.concurrent.locks.LockSupport;/*** author zhou* version 1.0* date 2023/10/16 9:11 下午*/ public class LockSupportDemo {public static void main(String[] args) {…...
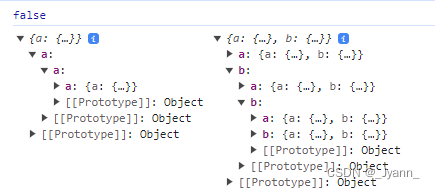
js深拷贝与浅拷贝
1.浅拷贝概念 浅拷贝是其属性与拷贝源对象的属性共享相同引用,当你更改源或副本时,也可能(可能说的是只针对引用数据类型)导致其他对象也发生更改。 特性: 会新创建一个对象,即objobj2返回fasle…...

Docker-harbor私有仓库部署与管理
搭建本地私有仓库 #首先下载 registry 镜像 docker pull registry #在 daemon.json 文件中添加私有镜像仓库地址 vim /etc/docker/daemon.json { "insecure-registries": ["20.0.0.50:5000"], #添加,注意用逗号结…...
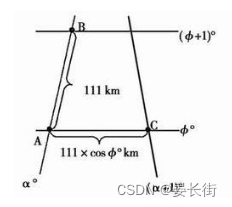
ArcGIS笔记8_测量得到的距离单位不是米?一经度一纬度换算为多少米?
本文目录 前言Step 1 遇到测量结果以度为单位的情况Step 2 简单的笨办法转换为以米为单位Step 3 拓展:一经度一纬度换算为多少米 前言 有时我们会遇到这种情况,想在ArcGIS中使用测量工具测量一下某一段距离,但显示的测量结果却是某某度&…...
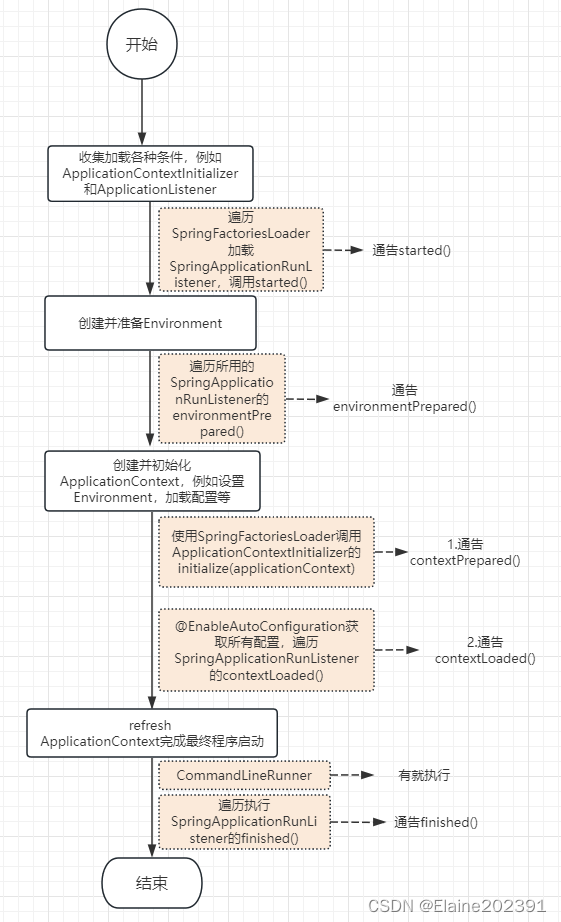
SpringBoot入门详解
目录 因何而生的SpringBoot 单体架构的捉襟见肘 SpringBoot的优点 快速入门 高曝光率的Annotation SpringBoot的工作机制 了解SpringBootApplication SpringBootConfiguration EnableAutoConfiguration 自动配置的幕后英雄:SpringFactoriesLoader Compon…...

数据分析案例-基于snownlp模型的MatePad11产品用户评论情感分析(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
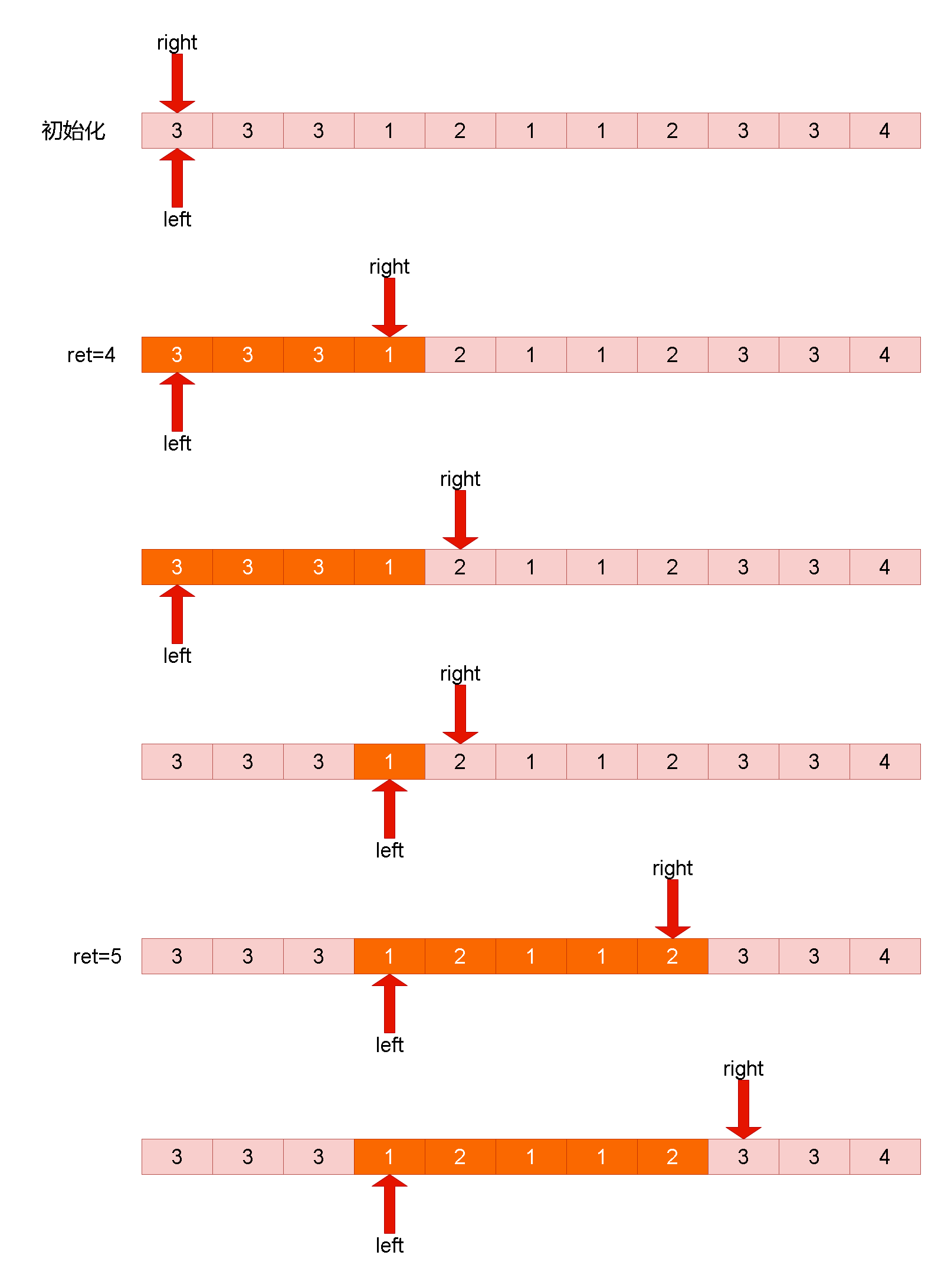
Leetcode刷题解析——904. 水果成篮
1. 题目链接:904. 水果成篮 2. 题目描述: 你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。 你想要尽可能多地收集水果。然而,农场的主…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
C++中vector类型的介绍和使用
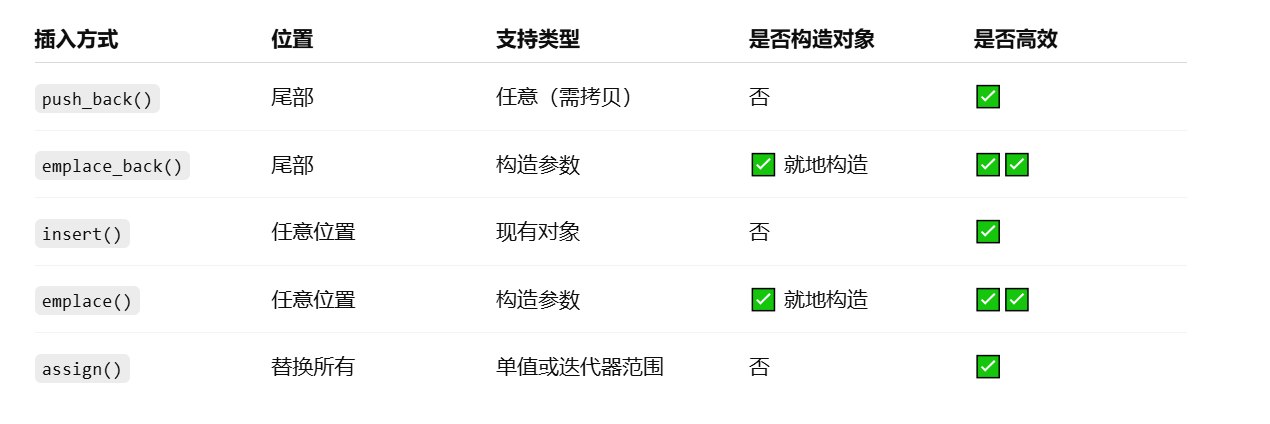
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...

ABB馈线保护 REJ601 BD446NN1XG
配电网基本量程数字继电器 REJ601是一种专用馈线保护继电器,用于保护一次和二次配电网络中的公用事业和工业电力系统。该继电器在一个单元中提供了保护和监控功能的优化组合,具有同类产品中最佳的性能和可用性。 REJ601是一种专用馈线保护继电器…...
SDU棋界精灵——硬件程序ESP32实现opus编码
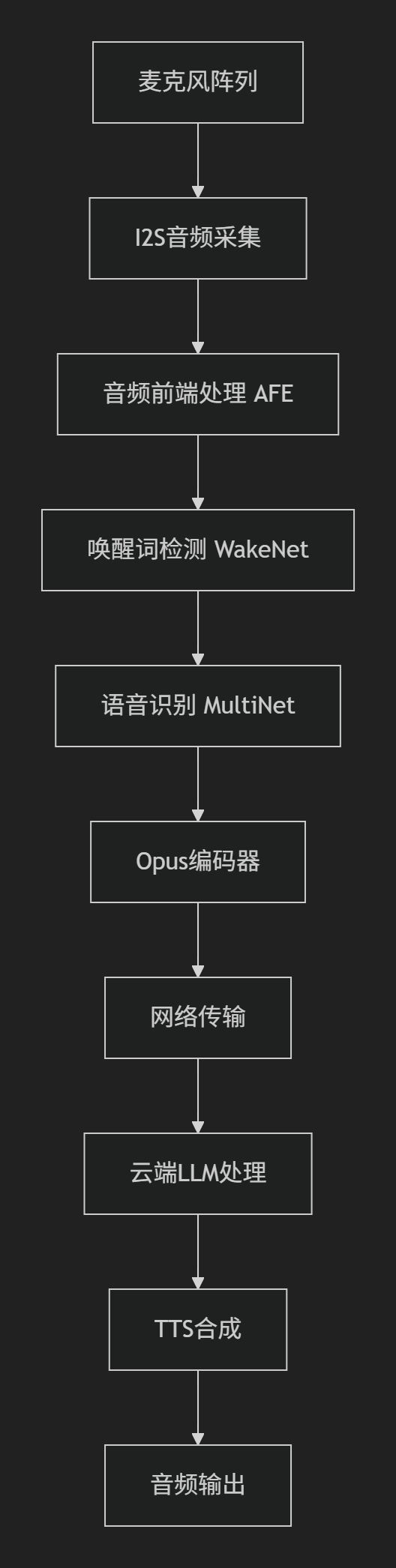
一、 音频处理框架 该项目基于Espressif的音频处理框架构建,核心组件包括 ESP-ADF 和 ESP-SR,以下是完整的音频处理框架实现细节: 1.核心组件 (1) 音频前端处理 (AFE - Audio Front-End) main/components/audio_pipeline/afe_processor.c功能: 声学回声…...
