【Overload游戏引擎细节分析】视图投影矩阵计算与摄像机
本文只罗列公式,不做具体的推导。
OpenGL本身没有摄像机(Camera)的概念,但我们为了产品上的需求与编程上的方便,一般会抽象一个摄像机组件。摄像机类似于人眼,可以建立一个本地坐标系。相机的位置是坐标原点,摄像机的朝向Forward是摄像机看的方向,再给定向上的Up轴即可建立本地坐标系。然后,可以通过矩阵将世界坐标系的物体变换到摄像机坐标系中,这个矩阵称为视图矩阵。通过改变摄像机的本地坐标系,可以产生场景漫游的效果。

1. 视图矩阵公式
视图矩阵是将物体坐标从世界空间坐标变换到相机本地坐标系中。计算视图矩阵需给定摄像机的位置 e y e \mathbf{eye} eye,焦点位置 t o \mathbf{to} to, Forward与Up所在平面的内的矢量 Y Y Y ,注意Y可以不与Forward垂直,我们可以通过叉乘获得摄像机的本地坐标系:
f w d = n o r m a l i z e ( e y e − t o ) r i g h t = n o r m a l i z e ( Y × f w d ) u p = n o r m a l i z e ( f w d × r i g h t ) \begin{aligned} & \mathbf{fwd} = normalize(\mathbf{eye}-\mathbf{to}) \\& \mathbf{right}=normalize(Y\times \mathbf{fwd}) \\& \mathbf{up} = normalize(\mathbf{fwd}\times\mathbf{right})\end{aligned} fwd=normalize(eye−to)right=normalize(Y×fwd)up=normalize(fwd×right)

LookAt矩阵等于:
L o o k A t = [ s i d e x s i d e y s i d e z − s i d e ⋅ e y e u p x u p y u p z − u p ⋅ e y e f w d x f w d x f w d x − f w d ⋅ e y e 0 0 0 1 ] LookAt= \begin{bmatrix} \mathbf{side}_x & \mathbf{side}_y & \mathbf{side}_z & -\mathbf{side}\cdot \mathbf{eye}\\ \mathbf{up}_x & \mathbf{up}_y & \mathbf{up}_z & -\mathbf{up}\cdot \mathbf{eye}\\ \mathbf{fwd}_x & \mathbf{fwd}_x & \mathbf{fwd}_x & -\mathbf{fwd}\cdot \mathbf{eye}\\ 0& 0 & 0 & 1 \end{bmatrix} LookAt= sidexupxfwdx0sideyupyfwdx0sidezupzfwdx0−side⋅eye−up⋅eye−fwd⋅eye1
Overload中计算视图矩阵代码:
OvMaths::FMatrix4 OvMaths::FMatrix4::CreateView(const float p_eyeX, const float p_eyeY, const float p_eyeZ, const float p_lookX, const float p_lookY, const float p_lookZ, const float p_upX, const float p_upY, const float p_upZ)
{const OvMaths::FVector3 eye(p_eyeX, p_eyeY, p_eyeZ); // 摄像机位置const OvMaths::FVector3 look(p_lookX, p_lookY, p_lookZ); // 摄像机焦点const OvMaths::FVector3 up(p_upX, p_upY, p_upZ); // 摄像机upconst OvMaths::FVector3 forward(eye - look); // 摄像机的Z轴FVector3::Normalize(forward);// cross得到right轴const OvMaths::FVector3 upXForward(OvMaths::FVector3::Cross(up, forward));FVector3::Normalize(upXForward);// cross得到Up轴,等价于Y轴const OvMaths::FVector3 v(OvMaths::FVector3::Cross(forward, upXForward));OvMaths::FMatrix4 View;View.data[0] = upXForward.x;View.data[1] = upXForward.y;View.data[2] = upXForward.z;View.data[3] = -OvMaths::FVector3::Dot(eye, upXForward);View.data[4] = v.x;View.data[5] = v.y;View.data[6] = v.z;View.data[7] = -OvMaths::FVector3::Dot(eye, v);View.data[8] = forward.x;View.data[9] = forward.y;View.data[10] = forward.z;View.data[11] = -OvMaths::FVector3::Dot(eye, forward);return View;
}
2. 投影矩阵
投影是将物体的光线投射到相机的近平面上,将3D物体变成2D图像,是将相机坐标空间转换到屏幕空间,类似于真实相机的曝光过程。投影有两种透视投影与正交投影。
透视投影:通过透视概念模仿我们看到的真实世界的方式,尝试让2D图像看起来像是3D的。物体近大远小,这样3D空间中有的平行线看起来就不再平行。
正投影:与透视投影相反,在视锥体中的物体不因其距离相机远近做任何调整,直接进行投影。正投影在CAD软件中使用广泛。

透视投影矩阵:
[ 2 Z n e a r R − L 0 R + L R − L 0 0 2 Z n e a r T − B T + B T − B 0 0 0 − Z f a r + Z n e a r Z f a r − Z n e a r − 2 Z n e a r Z f a r Z f a r − Z n e a r 0 0 − 1 0 ] \begin{bmatrix} \frac{2Z_{near}}{R-L} & 0 & \frac{R+L}{R-L} & 0\\ 0 & \frac{2Z_{near}}{T-B} & \frac{T+B}{T-B} & 0\\ 0 & 0 & -\frac{Z_{far}+Z_{near}}{Z_{far}-Z_{near}} & -\frac{2Z_{near}Z_{far}}{Z_{far}-Z_{near}} \\ 0 & 0 & -1 & 0 \end{bmatrix} R−L2Znear0000T−B2Znear00R−LR+LT−BT+B−Zfar−ZnearZfar+Znear−100−Zfar−Znear2ZnearZfar0
其中:
Z n e a r 、 Z f a r 是相机位置到近平面、远平面的距离 Z_{near}、Z_{far}是相机位置到近平面、远平面的距离 Znear、Zfar是相机位置到近平面、远平面的距离
R、L–投影平面左右边界的X坐标
T、B–投影平面上下边界的Y坐标
Overload中计算透视投影矩阵的代码:
OvMaths::FMatrix4 OvMaths::FMatrix4::CreateFrustum(const float p_left, const float p_right, const float p_bottom, const float p_top, const float p_zNear, const float p_zFar)
{const float maxView = 2.0f * p_zNear;const float width = p_right - p_left;const float height = p_top - p_bottom;const float zRange = p_zFar - p_zNear;FMatrix4 Frustum;Frustum.data[0] = maxView / width;Frustum.data[5] = maxView / height;Frustum.data[2] = (p_right + p_left) / width;Frustum.data[6] = (p_top + p_bottom) / height;Frustum.data[10] = (-p_zFar - p_zNear) / zRange;Frustum.data[14] = -1.0f;Frustum.data[11] = (-maxView * p_zFar) / zRange;Frustum.data[15] = 0.0f;return Frustum;
}
正投影矩阵:
[ 2 R − L 0 0 − R + L R − L 0 2 T − B 0 − T + B T − B 0 0 1 Z f a r − Z n e a r − Z n e a r Z f a r − Z n e a r 0 0 0 1 ] \begin{bmatrix} \frac{2}{R-L} & 0 & 0 & -\frac{R+L}{R-L} \\ 0 & \frac{2}{T-B} & 0 & -\frac{T+B}{T-B} \\ 0 & 0 & \frac{1}{Z_{far}-Z_{near}} & -\frac{Z_{near}}{Z_{far}-Z_{near}} \\ 0 & 0 & 0 & 1 \end{bmatrix} R−L20000T−B20000Zfar−Znear10−R−LR+L−T−BT+B−Zfar−ZnearZnear1
Overload中计算正投影矩阵的代码:
OvMaths::FMatrix4 OvMaths::FMatrix4::CreateOrthographic(const float p_size, const float p_aspectRatio, const float p_zNear, const float p_zFar)
{auto ortho = OvMaths::FMatrix4::Identity;const auto right = p_size * p_aspectRatio;const auto left = -right;const auto top = p_size;const auto bottom = -top;ortho(0, 0) = 2.0f / (right - left);ortho(1, 1) = 2.0f / (top - bottom);ortho(2, 2) = -2.0f / (p_zFar - p_zNear);ortho(0, 3) = -(right + left) / (right - left);ortho(1, 3) = -(top + bottom) / (top - bottom);ortho(2, 3) = -(p_zFar + p_zNear) / (p_zFar - p_zNear);ortho(3, 3) = 1.0f;return ortho;
}
3. 摄像机封装
Overload中摄像机类比较简单,主要是对上面两个矩阵计算的封装。每次就是的时候需传入摄像机的位置及转动四元数,计算完视图投影矩阵后保存到自己的字段中。代码比较简单,不再分析了。
相关文章:

【Overload游戏引擎细节分析】视图投影矩阵计算与摄像机
本文只罗列公式,不做具体的推导。 OpenGL本身没有摄像机(Camera)的概念,但我们为了产品上的需求与编程上的方便,一般会抽象一个摄像机组件。摄像机类似于人眼,可以建立一个本地坐标系。相机的位置是坐标原点,摄像机的朝…...

什么是云原生?零基础学云原生难吗?
伴随着云计算的浪潮,云原生概念也应运而生,而且火得一塌糊涂,但真正谈起“云原生”,大多数非 IT 从业者的认知往往仅限于将服务应用放入云端,在云上处理业务。实际上,云原生远不止于此。 现在越来越多的企…...
Ubuntu18.04下载安装基于使用QT的pcl1.13+vtk8.2,以及卸载
一、QVTKWidget、QVTKWidget2、QVTKOpenGLWidget、QVTKOpenGLNativeWidget 区别 1.Qt版本 Qt5.4以前版本:QVTKWidget2/QVTKWidget。 Qt5.4以后版本:QVTKOpenGLWidget/QVTKOpenGLWidget。 2.VTK版本(Qt版本为5.4之后) 在VTK8.2以前的版本:QVT…...
7 使用Docker容器管理的tomcat容器中的项目连接mysql数据库
1、查看容器的IP 1)进入容器 docker exec -it mysql-test /bin/bash 2)显示hosts文件内容 cat /etc/hosts 这里容器的ip为172.17.0.2 除了上面的方法外,也可以在容器外使用docker inspect查看容器的IP docker inspect mysql-test 以下为…...

双节前把我的网站重构了一遍
赶在中秋国庆假期前,终于将我的网站(https://spacexcode.com/[1])结构定好了,如之前所说,这个网站的定位就是作为自己的前端知识沉淀。内容大致从:前端涉及的基础知识分类汇总(知识库࿰…...

基于 nodejs+vue网上考勤系统
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
以数智化指标管理,驱动光伏能源行业的市场推进
近年来,碳中和、碳达峰等降低碳排放、提升环境健康度的政策和技术改进正在不断地被社会所认可和引起重视,也被越来越多的企业在生产运营和基础建设中列为重要目标之一。而光伏能源行业作为全球绿色能源、新能源的优秀解决方案,充分利用太阳能…...
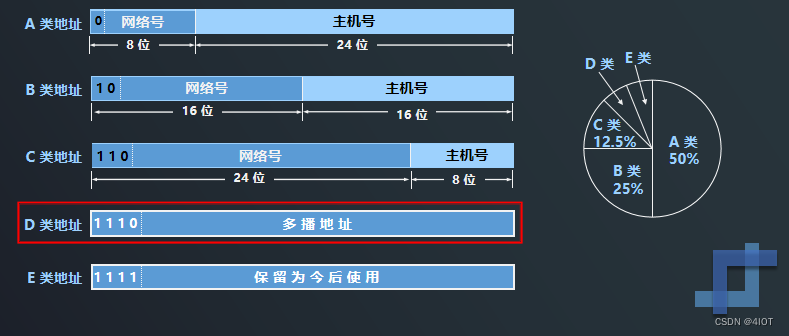
lv8 嵌入式开发-网络编程开发 18 广播与组播的实现
目录 1 广播 1.1 什么是广播? 1.2 广播地址 1.3 广播的实现 2 组播 2.1 分类的IP地址 2.2 多播 IP 地址 2.3 组播的实现 1 广播 1.1 什么是广播? 数据包发送方式只有一个接受方,称为单播 如果同时发给局域网中的所有主机࿰…...
)
前端面试题个人笔记(后面继续更新完善)
文章目录 填空题部分简答题部分 if有好答案请各位大佬们在底下评论上,感谢 填空题部分 1、常见的css选择器 2、getElementById获取元素的(DOM)对象 简答题部分 1、介绍一下你对RESTful API的理解以及它的优势? 答: …...
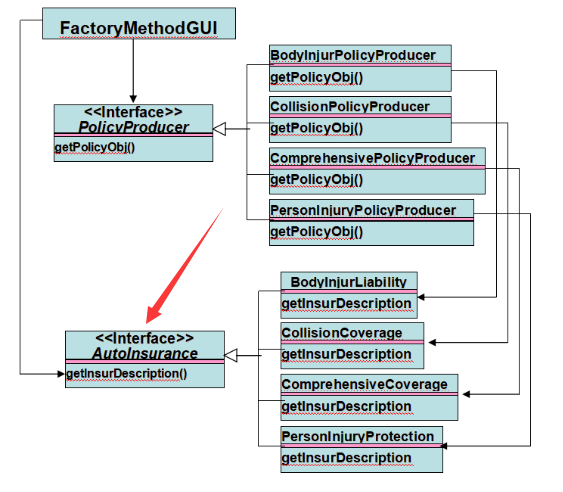
软件设计之工厂方法模式
工厂方法模式指定义一个创建对象的接口,让子类决定实例化哪一个类。 结构关系如下: 可以看到,客户端创建了两个接口,一个AbstractFactory,负责创建产品,一个Product,负责产品的实现。ConcreteF…...
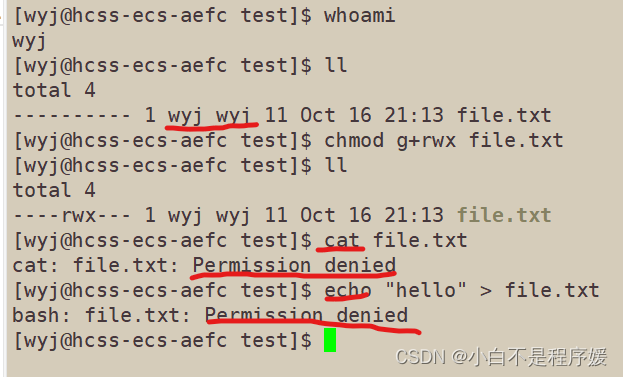
【Linux】shell运行原理及权限
主页点击直达:个人主页 我的小仓库:代码仓库 C语言偷着笑:C语言专栏 数据结构挨打小记:初阶数据结构专栏 Linux被操作记:Linux专栏 LeetCode刷题掉发记:LeetCode刷题 算法:算法专栏 C头疼…...

OA系统和ERP系统有什么区别?
在当今的企业管理领域,协同办公管理系统和ERP系统是两个非常重要的工具。它们在企业的日常运营中扮演着不同的角色,有着各自独特的功能和优势。那么,OA系统和ERP系统到底有什么区别呢?协同办公管理系统又是如何在这两者之间发挥协…...

c语言之strcat函数使用和实现
文章目录 前言一、strcat函数使用二、实现方法 前言 c语言之strcat 函数使用和实现 一、strcat函数使用 原型: char *strcat ( char * destination, const char * source );strcat追加拷贝,追加到目标空间后面,目标空间必须足够大,能容纳下…...
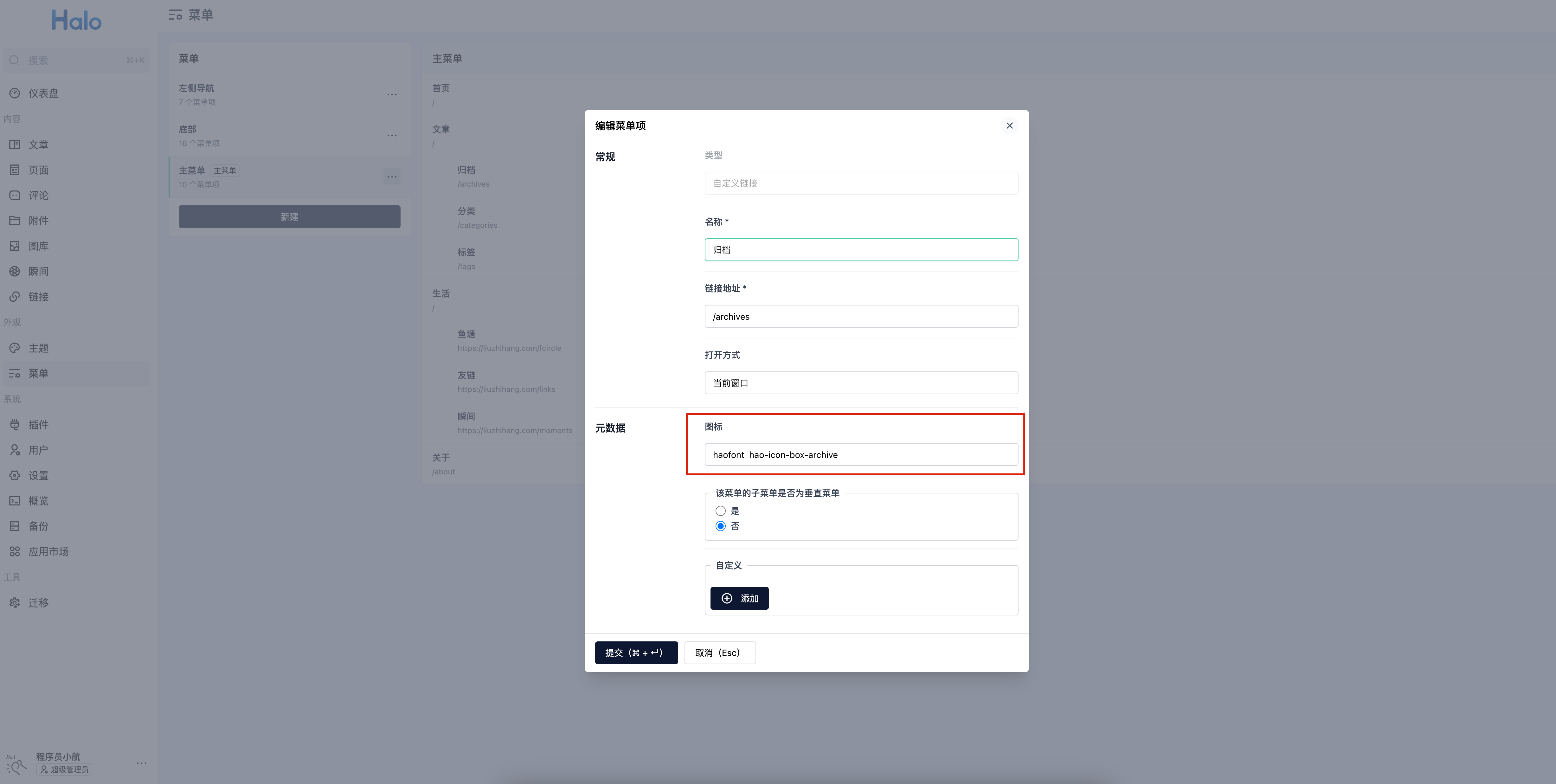
Halo-Theme-Hao文档:如何设置导航栏?
本篇文章会教你如何配置导航栏,最终效果参考如下。 感谢 Lanbin、小孙同学 等同学的贡献(语雀参与编辑)。 1标题 进入站点后台 点击左侧面板中的 主题 点击上方的 导航 修改 标题字段即可 2主菜单 主菜单即网站导航栏中间部分的菜单 进入站点…...

【Java学习之道】Java网络编程API介绍
引言 在Java中,进行网络编程的主要方式是通过Java网络编程API。这些API提供了一组类和接口,用于创建网络应用,如TCP和UDP通信、URL访问等。在这一节中,我们将带你领略Java网络编程API的魅力。 一、InetAddress InetAddress类是表…...
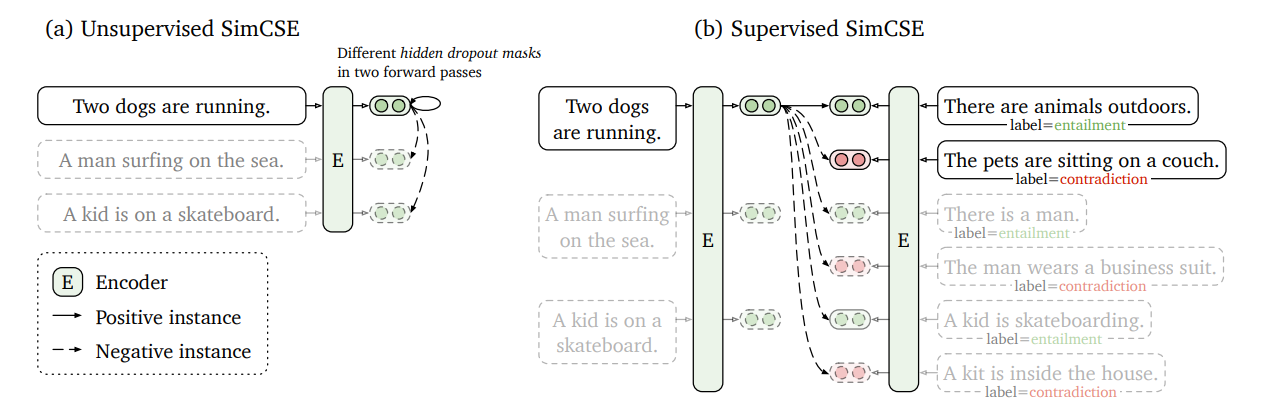
[论文笔记]SimCSE
引言 今天带来一篇当时引起轰动的论文SimCSE笔记,论文题目是 语句嵌入的简单对比学习。 SimCSE是一个简单的对比学习框架,它可以通过无监督和有监督的方式来训练。 对于无监督方式,输入一个句子然后在一个对比目标中预测它自己,仅需要标准的Dropout作为噪声。这种简单的…...

设置按键中断,按键1按下,LED亮,再按一次,灭按键2按下,蜂鸣器响。再按一次,不响按键3按下,风扇转,再按一次,风扇停
src/key_it.c #include"key_it.h" //GPIO初始化 void all_led_init() {//RCC使能RCC->MP_AHB4ENSETR | (0X1<<4);//设置PE10 PF10 PE8为输出GPIOE->MODER & (~(0X3<<20));GPIOE->MODER | (0X1<<20);//设置推挽输出GPIOE->OTYPER…...

深拷贝和浅拷贝的主要区别
在JavaScript中,深拷贝和浅拷贝的主要区别在于它们处理对象属性的方式。 浅拷贝(Shallow Copy)只复制对象的引用,而不是实际的对象。因此,如果你修改了复制的对象,原始对象也会受到影响。 深拷贝…...
Git Cherry Pick的使用
cherry-pick命令的基本用法 cherry-pick命令的基本语法如下: git cherry-pick <commit>其中,<commit>是要应用的提交的哈希值或分支名。该命令会将指定的提交应用到当前分支上,并创建一个新的提交。 使用场景 cherry-pick命令…...

vue3后台管理框架之基础配置
配置vite.config.js import { defineConfig } from viteimport vue from vitejs/plugin-vueexport default defineConfig(({ command, mode }) > {//const env loadEnv(mode, process.cwd(), ) //获取环境变量return {// 打包devbase: ./,// 开发环境server: {port: 5002,…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
