(五)物质导数与空间时间导数
本文内容主要包括:
1. 物质导数与空间时间导数及二者的联系
考虑运动变形过程中代表性物质点的物理量 Φ\bold\PhiΦ(张量) 随时间的变化率。
- 在物质描述中,Φ\bold\PhiΦ 以 (X⃗,t)(\vec{X},t)(X,t) 为自变量;
- 在空间描述中,Φ\bold\PhiΦ 以 (x⃗,t)(\vec{x},t)(x,t) 为自变量。
物理量 Φ\bold \PhiΦ 随某一固定的物质点一起运动的时间变化率(称作:物质导数)可写作:
DΦDt=(∂Φ(X⃗,t)∂t)∣X⃗≜Φ∙\dfrac{D\bold \Phi}{Dt} =\left. \left(\frac{\partial \bold\Phi(\vec{X},t)}{\partial t}\right)\right|_{\vec X} \triangleq \overset{\bullet}{\bold\Phi}DtDΦ=(∂t∂Φ(X,t))X≜Φ∙
物理量 Φ\bold \PhiΦ 在某一固定的空间坐标上的时间变化率(称作:空间时间导数/局部导数)可写作:
(∂Φ(x⃗,t)∂t)∣x⃗≜Φ′\left. \left(\frac{\partial \bold\Phi(\vec{x},t)}{\partial t}\right)\right|_{\vec x} \triangleq \bold\Phi'(∂t∂Φ(x,t))x≜Φ′
根据复合函数的求导法则可推出:
Φ∙={∂Φ[x⃗(X⃗,t),t]∂t}∣X⃗=(∂Φ∂t)∣x⃗+(∂Φ∂xr)(∂xr∂t)∣X⃗=Φ′+(∂Φ∂xr⊗g⃗r)⋅(g⃗s∂xs∂t)∣X⃗=Φ′+(Φ▽)⋅(∂x⃗∂t)∣X⃗=Φ′+(Φ▽)⋅(∂u⃗∂t)=Φ′+(Φ▽)⋅v⃗=Φ′+v⃗⋅(▽Φ)\begin{aligned} & \overset{\bullet}{\bold\Phi} =\left. \left\{\frac{\partial \bold\Phi[\vec{x}(\vec{X},t),t]}{\partial t}\right\}\right|_{\vec X} \\\\ &\quad=\left.\left(\dfrac{\partial\bold\Phi}{\partial t}\right)\right|_{\vec{x}}+\left(\dfrac{\partial\bold\Phi}{\partial {x}^r}\right)\left.\left(\dfrac{\partial x^r}{\partial t}\right)\right|_{\vec{X}}\\\\ &\quad=\bold\Phi'+\left(\dfrac{\partial\bold\Phi}{\partial {x}^r}\otimes\vec{g}\ ^r\right)\cdot\left.\left(\vec{g}_s\dfrac{\partial x^s}{\partial t}\right)\right|_{\vec{X}}\\\\ &\quad=\bold\Phi'+\left(\bold\Phi\triangledown\right)\cdot\left.\left(\dfrac{\partial\vec x}{\partial t}\right)\right|_{\vec{X}}\\\\ &\quad=\bold\Phi'+\left(\bold\Phi\triangledown\right)\cdot\left(\dfrac{\partial\vec u}{\partial t}\right)\\\\ &\quad=\bold\Phi'+\left(\bold\Phi\triangledown\right)\cdot\vec{v}\\\\ &\quad=\bold\Phi'+\vec{v}\cdot\left(\triangledown\bold\Phi\right) \end{aligned}Φ∙={∂t∂Φ[x(X,t),t]}X=(∂t∂Φ)x+(∂xr∂Φ)(∂t∂xr)X=Φ′+(∂xr∂Φ⊗g r)⋅(gs∂t∂xs)X=Φ′+(Φ▽)⋅(∂t∂x)X=Φ′+(Φ▽)⋅(∂t∂u)=Φ′+(Φ▽)⋅v=Φ′+v⋅(▽Φ)
2. 空间坐标系相关量的物质导数
2.1. 空间坐标系基矢的物质导数
随时间变化,某一固定物质点将映射至空间坐标系中的不同位置。因此,“空间坐标系基矢的物质导数”是指:某一物质点所在处的基矢变化率。故
g⃗i∙=(g⃗i)′+v⃗⋅▽g⃗i=v⃗⋅▽g⃗i=vj∂g⃗i∂xj=vjΓijkg⃗k=vjΓij,kg⃗k\overset{\bullet}{\vec{g}_i} =(\vec{g}_i)'+\vec{v}\cdot\triangledown\vec{g}_i =\vec{v}\cdot\triangledown\vec{g}_i =v^j\dfrac{\partial \vec{g}_i}{\partial x^j} =v^j\Gamma_{ij}^k\vec{g}_k =v^j\Gamma_{ij,k}\vec{g}^kgi∙=(gi)′+v⋅▽gi=v⋅▽gi=vj∂xj∂gi=vjΓijkgk=vjΓij,kgk
式中,Γijk、Γij,k\Gamma_{ij}^k、\Gamma_{ij,k}Γijk、Γij,k 分别为空间坐标系的第二类、第一类 Christoffel 符号。又由于
DDt(g⃗i⋅g⃗j)=g⃗i∙⋅g⃗j+g⃗i⋅g⃗j∙=0⟹g⃗i⋅g⃗j∙=−g⃗i∙⋅g⃗j\dfrac{D}{Dt}(\vec{g}_i\cdot\vec{g}^j) =\overset{\bullet}{\vec{g}_i}\cdot\vec{g}^j+\vec{g}_i\cdot\overset{\bullet}{\vec{g}^j} =0 \Longrightarrow \vec{g}_i\cdot\overset{\bullet}{\vec{g}^j}=-\overset{\bullet}{\vec{g}_i}\cdot\vec{g}^jDtD(gi⋅gj)=gi∙⋅gj+gi⋅gj∙=0⟹gi⋅gj∙=−gi∙⋅gj
令 g⃗j∙=βijg⃗i\overset{\bullet}{\vec{g}^j}=\beta^j_i\vec{g}^igj∙=βijgi ,那么:
g⃗i⋅βkjg⃗k=βij=−g⃗i∙⋅g⃗j=−vkΓikj\vec{g}_i\cdot\beta^j_k\vec{g}^k =\beta^j_i =-\overset{\bullet}{\vec{g}_i}\cdot\vec{g}^j =-v^k\Gamma^j_{ik}gi⋅βkjgk=βij=−gi∙⋅gj=−vkΓikj
故,
g⃗j∙=−vkΓikjg⃗i\overset{\bullet}{\vec{g}^j}=-v^k\Gamma^j_{ik}\vec{g}^igj∙=−vkΓikjgi
2.2. 空间坐标系协变基矢混合积的 g\sqrt{g}g 的物质导数
由空间坐标系基矢的物质导数可知:
gij∙=g⃗i∙⋅g⃗j+g⃗i⋅g⃗j∙=vr(Γirkgkj+Γjrkgki)=vr(Γir,j+Γjr,i)\overset{\bullet}{g_{ij}} =\overset{\bullet}{\vec{g}_i}\cdot\vec{g}_j+\vec{g}_i\cdot\overset{\bullet}{\vec{g}_j} =v^r(\Gamma^k_{ir}g_{kj}+\Gamma^k_{jr}g_{ki}) =v^r(\Gamma_{ir,j}+\Gamma_{jr,i})gij∙=gi∙⋅gj+gi⋅gj∙=vr(Γirkgkj+Γjrkgki)=vr(Γir,j+Γjr,i)
由于,
1det([A])[A∗]=[A]−1\dfrac{1}{det([A])}[A^*]=[A]^{-1}det([A])1[A∗]=[A]−1
其中,[A∗][A^*][A∗] 为 [A][A][A] 的伴随矩阵。则
1g∂g∂gji=gij,g=det(gij)\dfrac{1}{g}\dfrac{\partial g}{\partial g_{ji}}=g^{ij},g=det(g_{ij})g1∂gji∂g=gij,g=det(gij)
故,det(gij)det(g_{ij})det(gij) 的物质导数为:
g∙=∂g∂gjigji∙=ggijgji∙=gvr(Γiri+Γjrj)=2gvrΓiri\overset{\bullet}{g} =\dfrac{\partial g}{\partial g_{ji}}\overset{\bullet}{g_{ji}} =gg^{ij}\overset{\bullet}{g_{ji}} =gv^r(\Gamma_{ir}^i+\Gamma_{jr}^j) =2gv^r\Gamma_{ir}^ig∙=∂gji∂ggji∙=ggijgji∙=gvr(Γiri+Γjrj)=2gvrΓiri
式中,Γiri\Gamma_{ir}^iΓiri 为空间坐标系的第二类Christoffel 符号。进一步:
g∙=gvrΓiri\overset{\bullet}{\sqrt{g}}=\sqrt gv^r\Gamma_{ir}^ig∙=gvrΓiri
上式也可利用第二类Christoffel符号与协变基矢的混合积 g\sqrt{g}g 的关系与物质导数和局部导数的关系得到:
g∙=v⃗⋅(▽g)=vi∂g∂xi=gvrΓiri\overset{\bullet}{\sqrt{g}} =\vec{v}\cdot(\triangledown\sqrt{g}) =v^i\dfrac{\partial \sqrt{g}}{\partial x^i} =\sqrt gv^r\Gamma_{ir}^ig∙=v⋅(▽g)=vi∂xi∂g=gvrΓiri
3. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 相关量的物质导数
3.1. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 基矢的物质导数
随时间的变化,特定的物质点在随体坐标系 {XA,t}\{X^A,t\}{XA,t} 中的基矢不断改变。其协变基矢的变化率可写作:
C⃗A∙=[∂∂t(∂x⃗∂XA)]∣X⃗=[∂∂XA(∂x⃗∂t)]∣X⃗=∂∂XA(∂u⃗∂t)=∂v⃗∂XA=vB∣∣AC⃗B=∂v⃗∂xi∂xi∂XA=x,Ai∂v⃗∂xi=x,Aivj∣ig⃗j\begin{aligned} &\overset{\bullet}{\vec{C}_A} =\left.\left[\dfrac{\partial}{\partial t}\left(\dfrac{\partial \vec{x}}{\partial X^A}\right)\right]\right|_{\vec{X}} =\left.\left[\dfrac{\partial}{\partial X^A}\left(\dfrac{\partial \vec{x}}{\partial t}\right)\right]\right|_{\vec{X}} \\\ \\ &\quad\ =\dfrac{\partial}{\partial X^A}\left(\dfrac{\partial \vec{u}}{\partial t}\right) =\dfrac{\partial\vec{v}}{\partial X^A} =v^B||_A\vec{C}_B \\\ \\ &\quad\ =\dfrac{\partial\vec{v}}{\partial x^i}\dfrac{\partial x^i}{\partial X^A} =x^i_{,A}\dfrac{\partial\vec{v}}{\partial x^i} =x^i_{,A}v^j|_i\vec{g}_j \end{aligned} CA∙=[∂t∂(∂XA∂x)]X=[∂XA∂(∂t∂x)]X =∂XA∂(∂t∂u)=∂XA∂v=vB∣∣ACB =∂xi∂v∂XA∂xi=x,Ai∂xi∂v=x,Aivj∣igj
同理可知
C⃗A∙∙=∂a⃗∂XA=aB∣∣AC⃗B\overset{\bullet\bullet}{\vec{C}_A} =\dfrac{\partial\vec{a}}{\partial X^A} =a^B||_A\vec{C}_BCA∙∙=∂XA∂a=aB∣∣ACB
又
DC⃗A⋅C⃗BDt=C⃗A∙⋅C⃗B+C⃗A⋅C⃗B∙=0\dfrac{D{\vec{C}_A\cdot\vec{C}^B}}{Dt} =\overset{\bullet}{\vec{C}_A}\cdot\vec{C}^B+{\vec{C}_A}\cdot\overset{\bullet}{\vec{C}^B} =0DtDCA⋅CB=CA∙⋅CB+CA⋅CB∙=0
故
C⃗A∙=−(C⃗B∙⋅C⃗A)C⃗B=−vA∣∣BC⃗B=−X,jAvj∣ig⃗i\overset{\bullet}{\vec{C}^A} =-(\overset{\bullet}{\vec{C}_B}\cdot\vec{C}^A)\vec{C}^B =-v^A||_B\vec{C}^B =-X^A_{,\ j}v^j|_i\vec{g}^iCA∙=−(CB∙⋅CA)CB=−vA∣∣BCB=−X, jAvj∣igi
3.2. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 协变基矢混合积的 C\sqrt{C}C 的物质导数
C∙AB=C⃗∙A⋅C⃗B+C⃗A⋅C⃗∙B=vB∣∣A+vA∣∣B\overset{\bullet}{C}_{AB} =\overset{\bullet}{\vec C}_{A}\cdot{\vec C}_{B}+\vec{C}_A\cdot\overset{\bullet}{\vec C}_{B} =v_B||_A+v_A||_BC∙AB=C∙A⋅CB+CA⋅C∙B=vB∣∣A+vA∣∣B
又
1C∂C∂CBA=C−1AB,C=det(CAB)\dfrac{1}{C}\dfrac{\partial C}{\partial C_{BA}}=\overset{-1}{C}\ ^{AB},C=det(C_{AB})C1∂CBA∂C=C−1 AB,C=det(CAB)
则
C∙=∂C∂CBAC∙AB=CC−1ABC∙AB=C(vA∣∣A+vB∣∣B)=2CvA∣∣A\overset{\bullet}{C} =\dfrac{\partial C}{\partial C_{BA}}\overset{\bullet}{C}_{AB} =C\overset{-1}{C}\ ^{AB}\overset{\bullet}{C}_{AB} =C(v^A||_A+v^B||_B) =2Cv^A||_AC∙=∂CBA∂CC∙AB=CC−1 ABC∙AB=C(vA∣∣A+vB∣∣B)=2CvA∣∣A
进一步知:
C∙=12CC∙=CvA∣∣A\overset{\bullet}{\sqrt C} =\dfrac{1}{2\sqrt C}\overset{\bullet}{C} =\sqrt Cv^A||_AC∙=2C1C∙=CvA∣∣A
3.3. J\mathscr{J}J 的物质导数
由于,
J=det(F)=CG\mathscr{J}=det(\bold F)=\sqrt{\dfrac{C}{G}}J=det(F)=GC
故,
J∙=C∙G=CGvA∣∣A=JvA∣∣A=J▽⋅v⃗\overset{\bullet}{\mathscr{J}} ={\dfrac{\overset{\bullet}{\sqrt C}}{\sqrt G}} =\dfrac{\sqrt C}{\sqrt G}v^A||_A =\mathscr{J}v^A||_A =\mathscr{J}\triangledown\cdot\vec{v}J∙=GC∙=GCvA∣∣A=JvA∣∣A=J▽⋅v
4. 任意张量在空间坐标系与随体坐标系 {XA,t}\{X^A,t\}{XA,t} 中的物质导数
以三阶张量为例:
Φ=Φ∙∙kijg⃗i⊗g⃗j⊗g⃗k=Φ∙∙MABC⃗A⊗C⃗B⊗C⃗M\bold\Phi =\varPhi^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k =\varPhi^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\vec{C}_B\otimes\vec{C}^MΦ=Φ∙∙kij gi⊗gj⊗gk=Φ∙∙MAB CA⊗CB⊗CM
则
Φ∙=Φ∙∙∙MABC⃗A⊗C⃗B⊗C⃗M+Φ∙∙MABC⃗A∙⊗C⃗B⊗C⃗M+Φ∙∙MABC⃗A⊗C⃗B∙⊗C⃗M+Φ∙∙MABC⃗A⊗C⃗B⊗C⃗∙M=(Φ∙∙∙MAB+Φ∙∙MNBvA∣∣N+Φ∙∙MANvB∣∣N−Φ∙∙NABvN∣∣M)C⃗A⊗C⃗B⊗C⃗M\begin{aligned} &\overset{\bullet}{\bold\Phi} =\overset{\bullet}{\varPhi}\ ^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\vec{C}_B\otimes\vec{C}^M +\varPhi^{AB}_{\bullet\bullet M}\ \overset{\bullet}{\vec{C}_A}\otimes\vec{C}_B\otimes\vec{C}^M +\varPhi^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\overset{\bullet}{\vec{C}_B}\otimes\vec{C}^M +\varPhi^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\vec{C}_B\otimes\overset{\bullet}{\vec{C}}\ ^M \\\\ &\ \ \ =(\overset{\bullet}{\varPhi}\ ^{AB}_{\bullet\bullet M}+\varPhi^{NB}_{\bullet\bullet M}\ v^A||_N+\varPhi^{AN}_{\bullet\bullet M}\ v^B||_N-\varPhi^{AB}_{\bullet\bullet N}\ v^N||_M)\ \vec{C}_A\otimes\vec{C}_B\otimes\vec{C}^M \end{aligned}Φ∙=Φ∙ ∙∙MAB CA⊗CB⊗CM+Φ∙∙MAB CA∙⊗CB⊗CM+Φ∙∙MAB CA⊗CB∙⊗CM+Φ∙∙MAB CA⊗CB⊗C∙ M =(Φ∙ ∙∙MAB+Φ∙∙MNB vA∣∣N+Φ∙∙MAN vB∣∣N−Φ∙∙NAB vN∣∣M) CA⊗CB⊗CM
或
Φ∙=Φ∙∙∙kijg⃗i⊗g⃗j⊗g⃗k+Φ∙∙kijg⃗∙i⊗g⃗j⊗g⃗k+Φ∙∙kijg⃗i⊗g⃗∙j⊗g⃗k+Φ∙∙kijg⃗i⊗g⃗j⊗g⃗∙k=(Φ∙∙∙kij+Φ∙∙ksjvrΓrsi+Φ∙∙kisvrΓrsj−Φ∙∙sijvrΓrks)g⃗i⊗g⃗j⊗g⃗k=[(Φ∙∙kij)′+(vrΦ∙∙k,rij+Φ∙∙ksjvrΓrsi+Φ∙∙kisvrΓrsj−Φ∙∙sijvrΓrks)]g⃗i⊗g⃗j⊗g⃗k=[(Φ∙∙kij)′+vrΦ∙∙kij∣r)]g⃗i⊗g⃗j⊗g⃗k=Φ′+v⃗⋅▽Φ\begin{aligned} &\overset{\bullet}{\bold\Phi} =\overset{\bullet}{\varPhi}\ ^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k +\varPhi^{ij}_{\bullet\bullet k}\ \overset{\bullet}{\vec{g}}_i\otimes\vec{g}_j\otimes\vec{g}^k +\varPhi^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\overset{\bullet}{\vec{g}}_j\otimes\vec{g}^k +\varPhi^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\vec{g}_j\otimes\overset{\bullet}{\vec{g}}\ ^k \\\\ &\ \ \ =(\overset{\bullet}{\varPhi}\ ^{ij}_{\bullet\bullet k}+{\varPhi}\ ^{sj}_{\bullet\bullet k}v^r\Gamma^i_{rs}+{\varPhi}\ ^{is}_{\bullet\bullet k}v^r\Gamma^j_{rs}-{\varPhi}\ ^{ij}_{\bullet\bullet s}v^r\Gamma^s_{rk})\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k \\\\ &\ \ \ =[({\varPhi}\ ^{ij}_{\bullet\bullet k})'+(v^r{\varPhi}\ ^{ij}_{\bullet\bullet k,r}+{\varPhi}\ ^{sj}_{\bullet\bullet k}v^r\Gamma^i_{rs}+{\varPhi}\ ^{is}_{\bullet\bullet k}v^r\Gamma^j_{rs}-{\varPhi}\ ^{ij}_{\bullet\bullet s}v^r\Gamma^s_{rk})]\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k \\\\ &\ \ \ =[({\varPhi}\ ^{ij}_{\bullet\bullet k})'+v^r{\varPhi}\ ^{ij}_{\bullet\bullet k}|_r)]\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k \\\\ &\ \ \ =\bold\Phi'+\vec{v}\cdot\triangledown\bold\Phi \end{aligned}Φ∙=Φ∙ ∙∙kij gi⊗gj⊗gk+Φ∙∙kij g∙i⊗gj⊗gk+Φ∙∙kij gi⊗g∙j⊗gk+Φ∙∙kij gi⊗gj⊗g∙ k =(Φ∙ ∙∙kij+Φ ∙∙ksjvrΓrsi+Φ ∙∙kisvrΓrsj−Φ ∙∙sijvrΓrks) gi⊗gj⊗gk =[(Φ ∙∙kij)′+(vrΦ ∙∙k,rij+Φ ∙∙ksjvrΓrsi+Φ ∙∙kisvrΓrsj−Φ ∙∙sijvrΓrks)] gi⊗gj⊗gk =[(Φ ∙∙kij)′+vrΦ ∙∙kij∣r)] gi⊗gj⊗gk =Φ′+v⋅▽Φ
相关文章:
物质导数与空间时间导数)
(五)物质导数与空间时间导数
本文内容主要包括:1. 物质导数与空间时间导数及二者的联系2. 空间坐标系相关量的物质导数2.1. 空间坐标系基矢的物质导数2.2. 空间坐标系协变基矢混合积的 g\sqrt{g}g 的物质导数3. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 相关量的物质导数3.1. 随体坐标系 {XA,t}\{X^…...
)
python实战应用讲解-【语法基础篇】流程控制-运算符(附示例代码)
目录 比较运算符 相等运算符 is:相同运算符 in:成员资格运算符 字符串和序列的比较...
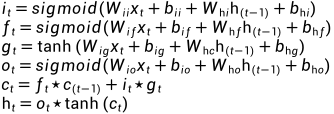
MXNet中使用双向循环神经网络BiRNN对文本进行情感分类
文本分类类似于图片分类,也是很常见的一种分类任务,将一段不定长的文本序列变换为文本的类别。这节主要就是关注文本的情感分析(sentiment analysis),对电影的评论进行一个正面情绪与负面情绪的分类。整理数据集第一步都是将数据集整理好&…...

SpringBoot 整合 MongoDB 6 以上版本副本集及配置 SSL / TLS 协议
续上一篇 Linux 中使用 docker-compose 部署 MongoDB 6 以上版本副本集及配置 SSL / TLS 协议 前提:此篇文章是对上一篇文章的实战和项目中相关配置的使用,我这边针对 MongoDB 原有基础上做了增强,简化了 MongoDB 配置 SSL / TLS 协议上的支…...
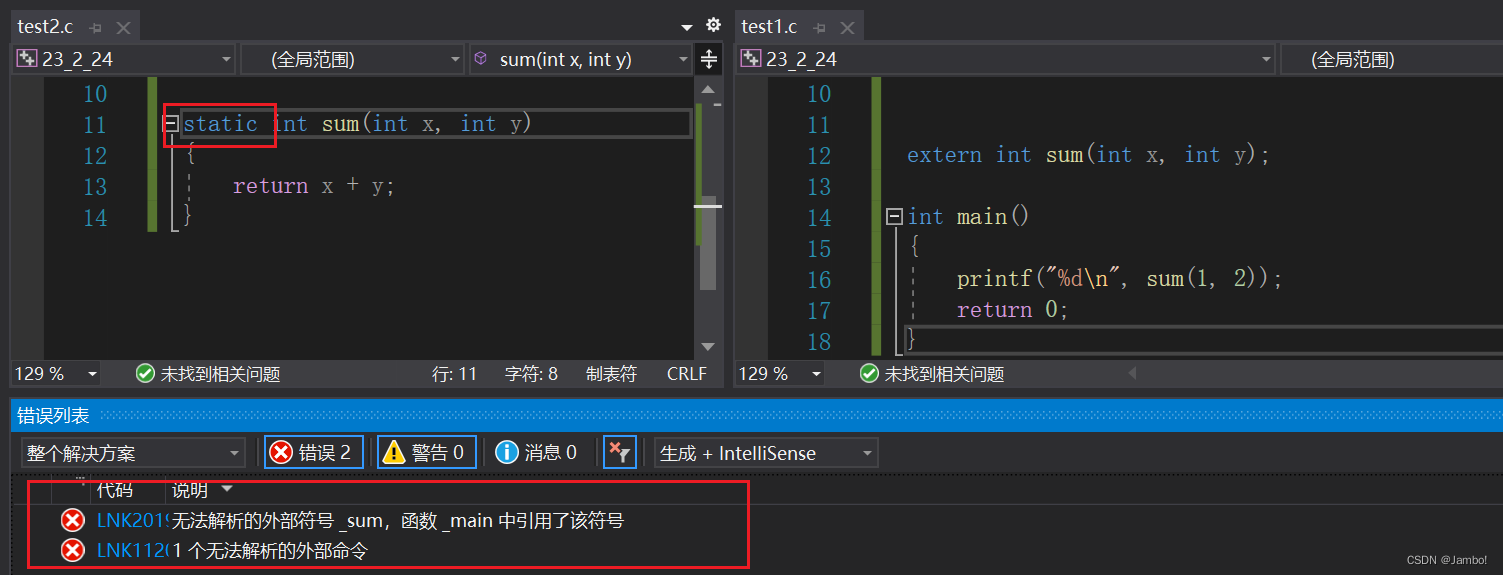
C语言static关键字
目录static修饰局部变量static修饰全局变量static修饰函数static是C语言的关键字,它有静态的意思static的三种用法:修饰局部变量修饰全局变量修饰函数 static修饰局部变量 我们先看一个程序: void print() {int a 0;a;printf("%d\n&…...

【华为OD机试模拟题】用 C++ 实现 - 单词接龙(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 货币单位换算(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 选座位(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 停车场最大距离(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 重组字符串(2023.Q1) 【华为OD机试模…...
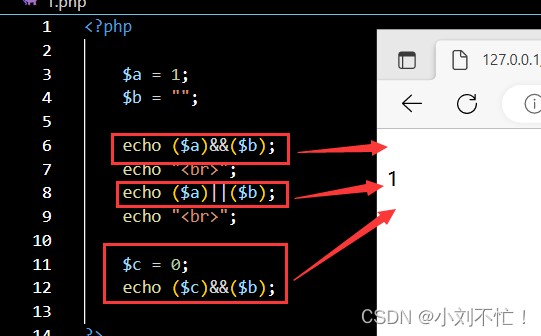
PHP基础(2)
PHP基础常用函数数组及多维数组数组遍历强制类型转换运算符赋值与基本运算字符串运算逻辑运算符常用函数 substr的用法是:substr(目标字符串,从字符串的哪个位置开始,然后返回往后的几个字符)strchr的用法是࿱…...
新特性)
Java8(JDK1.8)新特性
一、Java8(JDK1.8)新特性 1、Lamdba表达式 2、函数式接口 3、方法引用和构造引用 4、Stream API 5、接口中的默认方法和静态方法 6、新时间日期API 7、OPtional 8、其他特性 二、java8(JDK1.8)新特性简介 1、速度快; 2、代码少、简…...

【C语言】指针的定义和使用
指针一、什么是指针二、指针类型三、指针和数组的关系四、空指针五、野指针一、什么是指针 指针(Pointer)是编程语言中的一个对象,通过地址直接指向内存中该地址的值。由于通过地址能够找到所需的变量存储单元,可以说地址指向该变…...

Parameter ‘zpspid‘ not found
异常:nested exception is org.apache.ibatis.binding.BindingException: Parameter testypid not found. Available parameters are [ztpsXmjcxx, pageable, param1, param2]分析:以为是xml文件中没有对应的字段,一细看了几遍是有这个字段的…...
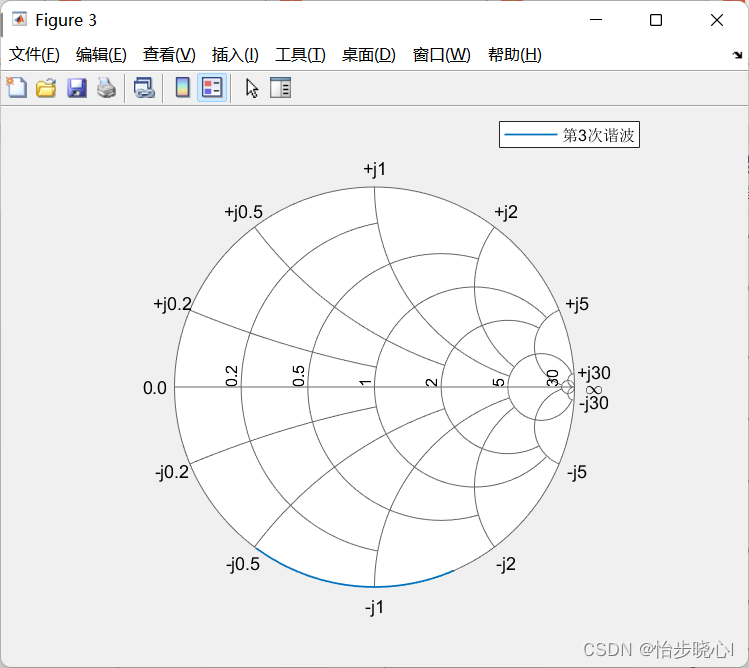
23、高自由度下的E类波形理论计算(附Matlab代码)
23、高自由度下的E类波形理论计算(附Matlab代码) 0、代码 任意占空比、电压导数条件下的E类波形与阻抗条件计算Matlab 注意修改路径,我这边是:!!!!!!&#…...
软件测试:用“bug”来表示“在电脑程序里的错误”
计算机基础知识计算机(personal computer)俗称电脑(pc),是现代一种用于高速计算的电子机器,可以进行数值计算,又可以进行逻辑判断,还具有存储记忆功能,且能够按照程序的运…...

Git命令
git init # 初始化本地git仓库(创建新仓库)git config --global user.name "xxx" # 配置用户名git config --global user.email "xxxxxx.com" # 配置邮件git config --global color.ui true # git status等命令自动着色git config -…...

Java的异常概念和类型
Java是一种流行的编程语言,拥有强大的异常处理机制,以帮助开发人员在程序出现异常时更好地处理错误情况。本文将介绍Java异常的概念和类型。异常的概念在Java中,异常是指在程序运行时发生的错误或异常情况。例如,当程序试图打开不…...

【Leedcode】环形链表必备的面试题和证明题(附图解)
环形链表必备的面试题和证明题(附图解) 文章目录环形链表必备的面试题和证明题(附图解)前言一、第一题1.题目2.思路3.代码4.延伸问题(1)证明题一:(2)证明题二:二、第二题1.题目2.思路延伸的证明题总结前言 …...

Vulnhub靶场----7、DC-7
文章目录一、环境搭建二、渗透流程三、思路总结一、环境搭建 DC-7下载地址:https://download.vulnhub.com/dc/DC-7.zip kali:192.168.144.148 DC-7:192.168.144.155 二、渗透流程 nmap -T5 -A -p- -sV -sT 192.168.144.155思路: …...
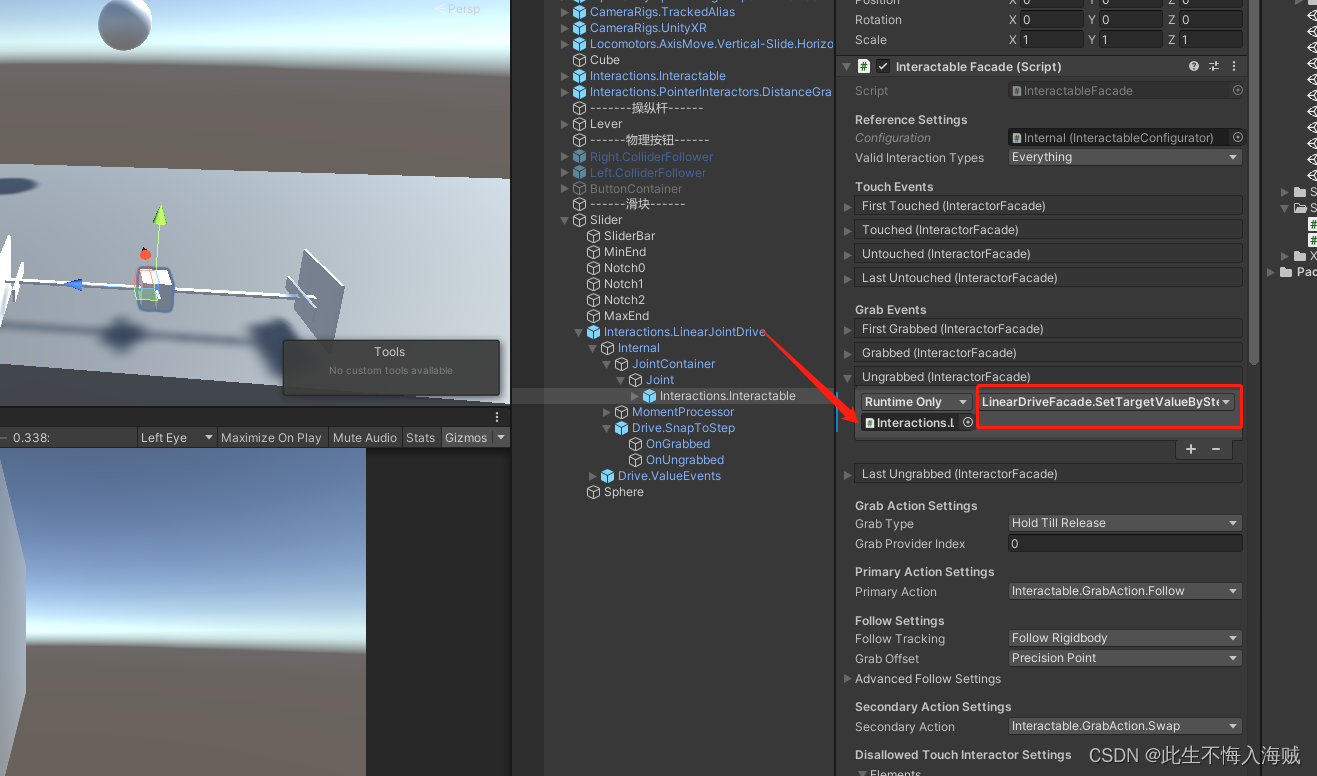
【Unity VR开发】结合VRTK4.0:创建滑块
语录: 只有经历地狱般的磨练,才能炼出创造天堂的力量。 前言: 滑块是一个非常简单的控件,它允许通过沿有限的驱动轴滑动 Interactable 来选择不同的值。我们将使用线性驱动器创建一个滑块控件,该控件允许我们根据与滑…...

Latex中的表格(2)
Latex中的表格一、一个加脚注的三线表的例子二、表格中加注释三、并排的表格3.1 使用小页环境并排表格3.2 使用子表格并排表格四、一个复杂的表格五、一个长表格这篇文章主要罗列一些特殊的表格例子。内容来自:一篇北师大学位论文模板,详见https://githu…...
输运定理)
(七)输运定理
本文主要内容包括:1. 物质积分2. 曲线上物质积分的时间变化率3. 曲面上物质积分的时间变化率4. 体积域上物质积分的时间变化率 (Reynolds 输运定理)1. 物质积分 考虑 t0t_0t0 时刻参考构型中由物质点 X⃗\vec{X}X所形成的 物质曲线 ct0c_{t_0}ct0、物质曲面 …...

ABBYYFineReader15免费电脑pdf文档文字识别软件
ABBYYFineReader是一款OCR文字识别软件,它可以对图片、文档等进行扫描识别,并将其转换为可编辑的格式,比如Word、Excel等,操作也是挺方便的。 我们在官网找到该软件并进行下载,打开软件后,选择转换为“Mic…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
