2023大联盟6比赛总结
比赛链接
反思
A
为什么打表就我看不出规律!!!
定式思维太严重了T_T
B
纯智障分块题,不知道为什么 B = 100 B=100 B=100 比理论最优 B = 300 B=300 B=300 更优(快了 3 倍),看来分块还是要学习一些卡常技巧的
C
菜死了,不会
D
菜死了,不会
题解
A
神奇的式子,考虑打表
打表!!!
可以发现一下两个规律:
- 只有当 x + y x+y x+y 是 2 2 2 的次幂时 f ( x , y ) f(x,y) f(x,y) 才可能不为 0 0 0
- f ( x , y ) = f ( x d , y d ) f(x,y)=f(\frac{x}{d},\frac{y}{d}) f(x,y)=f(dx,dy),其中 d = gcd ( x , y ) d=\gcd(x,y) d=gcd(x,y)
且若 x + y = 2 k , x , y x+y=2^k,x,y x+y=2k,x,y 都为奇数且 ( x , y ) = 1 (x,y)=1 (x,y)=1 时, f ( x , y ) = k f(x,y)=k f(x,y)=k
考虑证明:
考虑 x + y x+y x+y 必须为偶数因为一直循环下去 x + y x+y x+y 的值不变
f ( x , y ) = f ( x d , y d ) f(x,y)=f(\frac{x}{d},\frac{y}{d}) f(x,y)=f(dx,dy) 是易得的
我们只需要考虑 x , y x,y x,y 都为奇数的情况,因为 x , y x,y x,y 为偶数时 2 ∣ gcd ( x , y ) 2|\gcd(x,y) 2∣gcd(x,y)
令 x > y x>y x>y,则 f ( x , y ) = f ( 2 y , x − y ) + 1 f(x,y)=f(2y,x-y)+1 f(x,y)=f(2y,x−y)+1
因为 2 y , x − y 2y,x-y 2y,x−y 都为偶数,所以 f ( x , y ) = f ( y , x − y 2 ) + 1 f(x,y)=f(y,\frac{x-y}{2})+1 f(x,y)=f(y,2x−y)+1
这样 x ′ + y ′ x'+y' x′+y′ 的值就除了 2 2 2,且因为 gcd ( x , y ) = 1 \gcd(x,y)=1 gcd(x,y)=1,所以 gcd ( y , x − y 2 ) = 1 \gcd(y,\frac{x-y}{2})=1 gcd(y,2x−y)=1
所以 x + y x+y x+y 只有当是 2 2 2 的次幂时, x ′ = y ′ x'=y' x′=y′,且操作次数为 l o g 2 ( x + y ) log_2(x+y) log2(x+y)
我们发现这有值的点对个数是 O ( n l o g n ) O(nlogn) O(nlogn) 级别的
所以我们可以把所有有值的点对找出来,然后询问就相当于二维数点了
离线询问 + 扫描线 + 树状数组即可
时间复杂度 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
#include <bits/stdc++.h>
#define pb push_back
#define lowbit(x) x&-x
using namespace std;
typedef long long LL;
const int N=300100,Q=1000100;
struct Node{ int p1,p2,val;};
struct Node2{ int l,r,id,coef;};
int n,p[N],b[N];
LL tr[N],ans[Q];
Node used[N*40];
vector<Node2> query[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
bool cmp(const Node &x,const Node &y){ return x.p1<y.p1;}
void add(int x,int v){ for(;x<=n;x+=lowbit(x)) tr[x]+=v;}
LL ask(int x){if(x<=0) return 0;LL res=0;for(;x;x-=lowbit(x)) res+=tr[x];return res;
}
int main(){freopen("perm.in","r",stdin);freopen("perm.out","w",stdout);n=read();for(int i=1;i<=n;i++) p[i]=read(),b[p[i]]=i;int cnt=0;for(int pw=4,mi=2;pw<=n<<1;pw<<=1,mi++)for(int x=1;x<=pw;x+=2){int y=pw-x;for(int k=1;k*max(x,y)<=n;k++) used[++cnt]={b[x*k],b[y*k],mi};}int q=read();for(int i=1;i<=q;i++){int l=read(),r=read();query[l-1].pb({l,r,i,-1}),query[r].pb({l,r,i,1});}sort(used+1,used+cnt+1,cmp);for(int i=1,j=0;i<=n;i++){while(j<cnt&&used[j+1].p1<=i){j++;assert(used[j].p2>=1&&used[j].p2<=n);add(used[j].p2,used[j].val);}for(Node2 t:query[i]) ans[t.id]+=t.coef*(ask(t.r)-ask(t.l-1));}for(int i=1;i<=q;i++) printf("%lld\n",ans[i]/2);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}B
不说了,思想比较简单,就是分块 + 块内用优先队列维护
时间复杂度 O ( n m l o g n ) O(n\sqrt mlogn) O(nmlogn), m m m 为修改操作个数
块长设为 100 100 100 实测最优
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N=100100,MAXB=1010,P=1e9+7;
typedef pair<int,int> pii;
int n,m,a[N],pref[N],pos[N];
int B,sum[MAXB],tot[MAXB],tag[MAXB],_l[MAXB],_r[MAXB];
priority_queue<pii,vector<pii>,greater<pii> > pq[MAXB];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline int calc(int x){int cur=sqrt(x);return (pref[cur-1]+1ll*(x-cur*cur+1)*cur)%P;
}
inline void inc(int &x,int y){ x+=y;if(x>=P) x-=P;}
void rebuild(int Block){for(int i=_l[Block];i<=_r[Block];i++) a[i]+=tag[Block];tag[Block]=tot[Block]=sum[Block]=0;while(!pq[Block].empty()) pq[Block].pop();for(int i=_l[Block];i<=_r[Block];i++){int sq=sqrt(a[i]);inc(tot[Block],calc(a[i])),inc(sum[Block],sq);pq[Block].emplace(make_pair((sq+1)*(sq+1)-a[i],i));}assert(tot[Block]>=0);
}
void modify(int l,int r){if(pos[l]==pos[r]){for(int i=l;i<=r;i++) a[i]++;rebuild(pos[l]);return;}else{int i=l,j=r;while(pos[i]==pos[l]) a[i]++,i++;while(pos[j]==pos[r]) a[j]++,j--;rebuild(pos[l]),rebuild(pos[r]);for(int k=pos[i];k<=pos[j];k++){tag[k]++;pii t=pq[k].top();while(t.first<=tag[k]){pq[k].pop();inc(sum[k],1);int v=sqrt(a[t.second]+tag[k]);assert(v*v==a[t.second]+tag[k]);pq[k].push(make_pair((v+1)*(v+1)-a[t.second],t.second));t=pq[k].top();}inc(tot[k],sum[k]);}}
}
int query(int l,int r){int ans=0;if(pos[l]==pos[r]){rebuild(pos[l]);for(int i=l;i<=r;i++) inc(ans,calc(a[i]));}else{rebuild(pos[l]),rebuild(pos[r]);int i=l,j=r;while(pos[i]==pos[l]) inc(ans,calc(a[i])),i++;while(pos[j]==pos[r]) inc(ans,calc(a[j])),j--;for(int k=pos[i];k<=pos[j];k++) inc(ans,tot[k]);}return ans;
}
int main(){freopen("play.in","r",stdin);freopen("play.out","w",stdout);for(int i=1;i<=40000;i++) pref[i]=(pref[i-1]+((1ll*(i+1)*(i+1)-1ll*i*i)%P+P)*i)%P;for(int i=1;i<=40000;i++) assert(pref[i]>=0);n=read(),m=read();for(int i=1;i<=n;i++) a[i]=read();B=100;for(int i=1;i<=n;i++) pos[i]=(i-1)/B+1;for(int i=1;i<=pos[n];i++) _l[i]=_r[i-1]+1,_r[i]=i*B;_r[pos[n]]=n;for(int i=1;i<=pos[n];i++) rebuild(i);for(int i=1;i<=m;i++){int op=read(),l=read(),r=read();if(op==1) modify(l,r);else printf("%d\n",query(l,r));}fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}C
感觉是到有点 nb 的题
不考虑翻转,如何求 l i s lis lis?
考虑枚举分界点 i i i,那么答案 = max { i 前面 0 的个数 + i 后面 1 的个数 } =\max\{i前面0的个数+i后面1的个数\} =max{i前面0的个数+i后面1的个数}
这等价于 s 1 + max i = 1 n s u m i s1+\max\limits_{i=1}^{n} sum_i s1+i=1maxnsumi,其中 s 1 s1 s1 为序列中 1 1 1 的个数, s u m i sum_i sumi 为把 0 0 0 的权值设为 1 1 1, 1 1 1 的权值设为 − 1 -1 −1 的前缀和
考虑翻转操作
我们可以把这个问题等价地看成选出一段前缀和与 m m m 段不相交子区间(不能与前缀相交)的和的最大值
这一步感觉很难想,也很难理解
具体我也不会证,只能自己画图感性理解
然后就是经典的反悔贪心操作了,找最大的区间,然后区间取反,用线段树维护即可
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=200100;
int n,val[N],s[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
struct Node{int l,r,sum;int lmx,rmx,mx,Lp,Rp,LLp,RRp;int lmn,rmn,mn,Lq,Rq,LLq,RRq;bool tag;
}seg[N<<2];
Node operator +(const Node &lc,const Node rc){Node ret;ret.l=lc.l,ret.r=rc.r,ret.tag=0;ret.sum=lc.sum+rc.sum;ret.lmx=lc.lmx,ret.LLp=lc.LLp;if(lc.sum+rc.lmx>ret.lmx) ret.lmx=lc.sum+rc.lmx,ret.LLp=rc.LLp;ret.rmx=rc.rmx,ret.RRp=rc.RRp;if(rc.sum+lc.rmx>ret.rmx) ret.rmx=rc.sum+lc.rmx,ret.RRp=lc.RRp;ret.mx=lc.rmx+rc.lmx,ret.Lp=lc.RRp,ret.Rp=rc.LLp;if(lc.mx>ret.mx) ret.mx=lc.mx,ret.Lp=lc.Lp,ret.Rp=lc.Rp;if(rc.mx>ret.mx) ret.mx=rc.mx,ret.Lp=rc.Lp,ret.Rp=rc.Rp;ret.lmn=lc.lmn,ret.LLq=lc.LLq;if(lc.sum+rc.lmn<ret.lmn) ret.lmn=lc.sum+rc.lmn,ret.LLq=rc.LLq;ret.rmn=rc.rmn,ret.RRq=rc.RRq;if(rc.sum+lc.rmn<ret.rmn) ret.rmn=rc.sum+lc.rmn,ret.RRq=lc.RRq;ret.mn=lc.rmn+rc.lmn,ret.Lq=lc.RRq,ret.Rq=rc.LLq;if(lc.mn<ret.mn) ret.mn=lc.mn,ret.Lq=lc.Lq,ret.Rq=lc.Rq;if(rc.mn<ret.mn) ret.mn=rc.mn,ret.Lq=rc.Lq,ret.Rq=rc.Rq;return ret;
}
void down(int x){swap(seg[x].lmx,seg[x].lmn),swap(seg[x].rmx,seg[x].rmn),swap(seg[x].mx,seg[x].mn);swap(seg[x].Lp,seg[x].Lq),swap(seg[x].Rp,seg[x].Rq),swap(seg[x].LLp,seg[x].LLq),swap(seg[x].RRp,seg[x].RRq);seg[x].sum*=-1,seg[x].lmx*=-1,seg[x].rmx*=-1,seg[x].mx*=-1,seg[x].lmn*=-1,seg[x].rmn*=-1,seg[x].mn*=-1;seg[x].tag^=1;
}
void pushdown(int x){if(seg[x].tag) down(x<<1),down(x<<1^1);seg[x].tag=0;
}
void build(int l,int r,int x){if(l==r){ seg[x]={l,l,val[l],val[l],val[l],val[l],l,l,l,l,val[l],val[l],val[l],l,l,l,l,0};return;}int mid=(l+r)>>1; build(l,mid,x<<1),build(mid+1,r,x<<1^1);seg[x]=seg[x<<1]+seg[x<<1^1];
}
void modify(int l,int r,int x,int L,int R){if(L<=l&&r<=R){ down(x);return;}pushdown(x);int mid=(l+r)>>1;if(mid>=L) modify(l,mid,x<<1,L,R);if(mid<R) modify(mid+1,r,x<<1^1,L,R);seg[x]=seg[x<<1]+seg[x<<1^1];
}
signed main(){freopen("lis.in","r",stdin);freopen("lis.out","w",stdout);n=read();int ans=0;for(int i=1;i<=n;i++){int a=read(),b=read();if(a==0) a=1;else a=-1,ans+=b;val[i]=a*b,s[i]=s[i-1]+val[i];}int mx=0;s[0]=-1e18;for(int i=1;i<=n;i++) if(s[i]>s[mx]) mx=i;build(1,n,1);if(s[mx]>0) ans+=s[mx],modify(1,n,1,1,mx);printf("%lld\n",ans);int m=read();for(int i=1;i<=m;i++){Node ret=seg[1];if(ret.mx>0) ans+=ret.mx,modify(1,n,1,ret.Lp,ret.Rp);printf("%lld\n",ans);}fprintf(stderr,"%d ms\n",int64_t(1e3*clock()/CLOCKS_PER_SEC));return 0;
}D
考虑暴力是 f i , j f_{i,j} fi,j 表示当前在 i i i,前一个选 j j j 的最大长度,因为 p i ≠ k p_i\neq k pi=k 的限制很松,所以直接记录最大值和次大值就可以维护,时间复杂度 O ( n 3 ) O(n^3) O(n3)
于是我们可以猜测需要保留的转移状态不会太多,事实上是真的
我们令三元组 ( l e n t h , p r e , i ) (lenth,pre,i) (lenth,pre,i) 表示当前在 i i i,上一个在 p r e pre pre,长度为 l e n t h lenth lenth 的状态
我们考虑用这个东西转移
每次答案,我们需要把 a j < a i a_j<a_i aj<ai 的 ( l e n t h , p r e , j ) (lenth,pre,j) (lenth,pre,j) 取出,然后更新 i i i 的状态
结论1:对于 i i i 只需要保留 l e n t h lenth lenth 最长的两个且满足 j p ≠ j q j_p\neq j_q jp=jq 的状态
首先 j j j 相等的状态只需要保留一个,那么后面最多只会排除掉 1 1 1 个状态,所以只需要暴力 2 2 2 个状态
结论2:只需要取出 ( l e n t h , p r e , j ) (lenth,pre,j) (lenth,pre,j) 的前 5 5 5 大 l e n t h lenth lenth,且对于 p r e pre pre 相同的,我们只保留最大的 2 2 2 个
为什么,考虑如果前两个的 p r e pre pre 都和 i i i 一样,那么后两个必然有两个 p r e pre pre 不相同的,是可以更新出 2 2 2 个有效答案的
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)(但常数有点大,我稍微卡了一下常)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define pb push_back
#define lowbit(x) x&-x
using namespace std;
const int N=200100;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
struct Node{ int lenth,pre,x;//以x结尾的长度为lenth的序列,前一个为pre的一种转移
};
vector<Node> tr[N];
int n,a[N],p[N],cnt[N];
bool cmp(const Node &o1,const Node &o2){ return o1.lenth>o2.lenth;}
auto select(vector<Node> vec){sort(vec.begin(),vec.end(),cmp);vector<Node> ret;for(auto t:vec){int c=0;for(auto q:ret) if(q.pre==t.pre) c++;if(c==2) continue;ret.pb(t);if(ret.size()==5) break;}return ret;
}
const int B=20;
void add(int x,vector<Node> ad){for(;x<=n;x+=lowbit(x)){for(auto t:ad) tr[x].pb(t);if(tr[x].size()>=B) tr[x]=select(tr[x]);}
}
auto query(int x){vector<Node> ret;for(;x;x-=lowbit(x)) for(auto t:tr[x]) ret.pb(t);return ret;
}
void work(){n=read();for(int i=1;i<=n;i++) a[i]=read();for(int i=1;i<=n;i++) p[i]=read();int ans=0;for(int i=1;i<=n;i++){auto ret=query(a[i]-1);ret.pb({0,-1,-1});//以i为开头ret=select(ret);vector<Node> cur;for(auto t:ret)if(p[i]!=t.pre)if(!cur.size()||t.x!=cur.back().pre){cur.pb({t.lenth+1,t.x,i});if(cur.size()==2) break;}for(auto t:cur) ans=max(ans,t.lenth);add(a[i],cur);}printf("%d\n",ans);for(int i=1;i<=n;i++) tr[i].clear();
}
int main(){freopen("cactus.in","r",stdin);freopen("cactus.out","w",stdout);int T=read();while(T--) work();fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}相关文章:

2023大联盟6比赛总结
比赛链接 反思 A 为什么打表就我看不出规律!!! 定式思维太严重了T_T B 纯智障分块题,不知道为什么 B 100 B100 B100 比理论最优 B 300 B300 B300 更优(快了 3 倍),看来分块还是要学习一…...
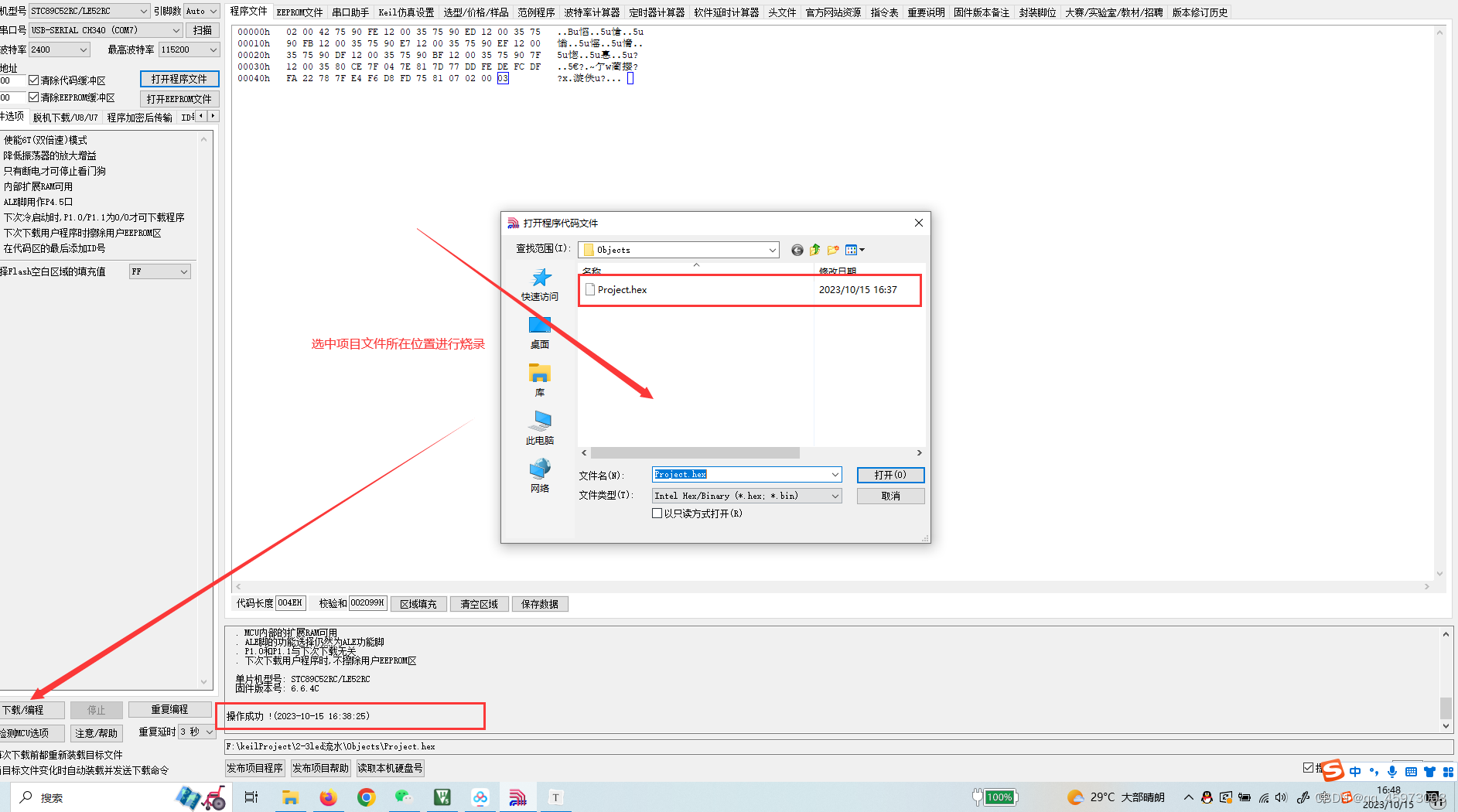
05_51单片机led流水线的实现
1:step创建一个新的项目并将程序烧录进入51单片机 以下是51单片机流水线代码的具体实现 #include <REGX52.H>void Delay500ms() //11.0592MHz {unsigned char i, j, k;i 4;j 129;k 119;do{do{while (--k);} while (--j);} while (--i); }void main(){while(1){P1 0…...
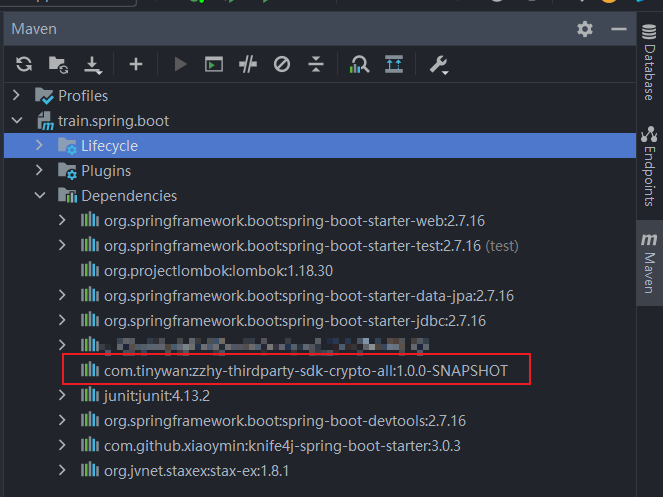
Java系列 | 如何讲自己的JAR包上传至阿里云maven私有仓库【云效制品仓库】
什么是云效 云效是云原生时代一站式 BizDevOps 平台,产研数字化同行者,支持公共云、专有云和混合云多种部署形态,通过云原生新技术和研发新模式,助力创新创业和数字化转型企业快速实现产研数字化,打造“双敏”组织&…...

小程序技术加速信创操作系统国产化替换
随着信息技术的不断发展,信息技术应用创新(简称“信创”)已经成为了当今企业数字化转型的重要趋势之一。信创是指在信息技术领域,以自主可控的国产软硬件产品和服务为核心,构建起一套完整的信息技术生态体系࿰…...
免费:实时 AI 编程助手 Amazon CodeWhisperer
点 ,一起程序员弯道超车之路 现已正式推出实时 AI 编程助手 Amazon CodeWhisperer,包括 CodeWhisperer 个人套餐,所有开发人员均可免费使用。最初于去年推出的预览版 CodeWhisperer 让开发人员能够保持专注、高效,帮助他们快速、安…...

面试准备-深入理解计算机系统-信息的表示与处理1
浮点运算是不可结合的(由于表示的精度有限)。比如(3.141e20)-1e20是0.0而3.14(1e20-1e20)是3.14。整数虽然只能编码一个较小的取值范围,但是是准确的;浮点数虽然能编码更大的范围,但是是近似的。 二进制转十六进制转换…...

搭建Atlas2.2.0 集成CDH6.3.2 生产环境+kerberos
首先确保环境的干净,如果之前有安装过清理掉相关残留 确保安装atlas的服务器有足够的内存(至少16G),有必要的hadoop角色 HDFS客户端 — 检索和更新Hadoop使用的用户组信息(UGI)中帐户成员资格的信息。对调…...
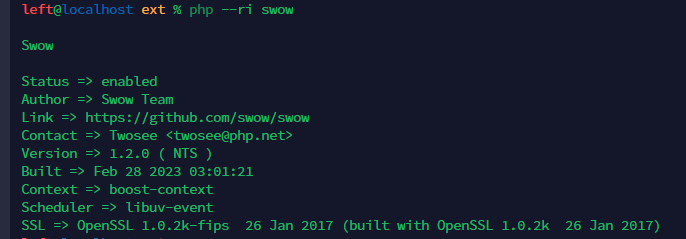
【运维笔记】swow源码编译安装
swow的github网址 https://github.com/swow/swow 从github中拉取源码 git pull https://github.com/swow/swow.git 编译安装 github中readme文件讲述了安装方法 这里整理了命令,进入拉取项目的目录后依次执行命令即可 #pwd 确保自己在swow目录中,如…...

【2023/10/16 下午10:32:39】
2023/10/16 下午10:32:39 BOOL Create(LPCTSTR strTitle, DWORD dwStyle, const RECT &rect, CWnd *pwndParent, DWORD dwPaletteSetStyle = PSS_PROPERTIES_MENU | PSS_AUTO_ROLLUP | PSS_CLOSE_BUTTON | PSS_SNAP); 2023/10/16 下午10:32:46 这是一个函数声明,看起来…...
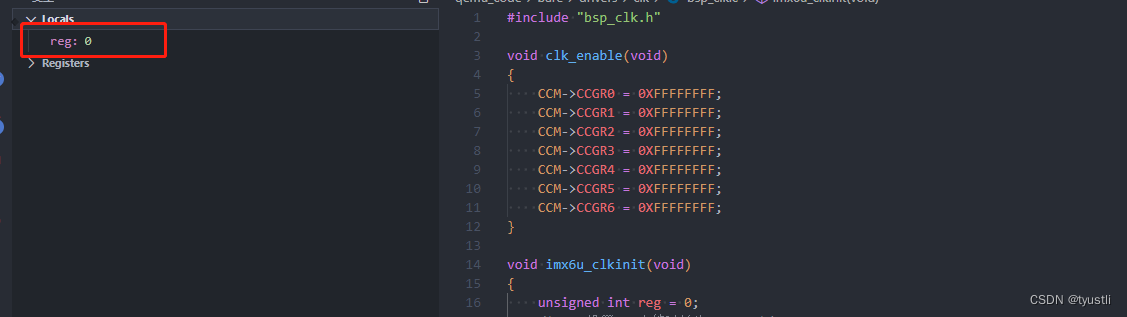
qemu基础篇——VSCode 配置 GDB 调试
文章目录 VSCode 配置 GDB 调试安装 VSCode 插件调试文件创建调试配置配置脚本qemu 启动脚 启动调试报错情况一报错情况二报错情况三 调试界面运行 GDB 命令查看反汇编断点查看内核寄存器查看变量参考链接 VSCode 配置 GDB 调试 qemu-基础篇——arm 裸机调试环境搭建 上一节中…...

Spark常用算子
转换算子 value类型 算子名称作用Map映射a->bflatMap扁平化[[a,b],[c,d]] -> [a,b,c,d] ,二维变一维groupBy分组[1,2,3,4] ->[[1,3],[2,4] ],一维变二维filter过滤[1,2,3,4] -> [2,4] 符合条件进入,不符合去掉distinct去重[1,1…...
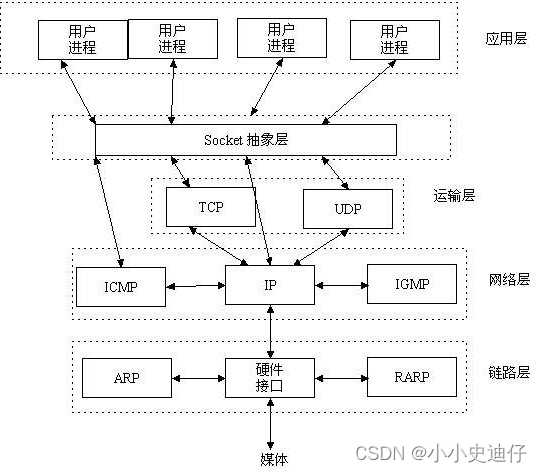
day35
今日内容概要 Socket抽象层(socket编程) 基于TCP协议的借助socket可以编程客户端和服务端的程序 链接循环 通信循环 基于UDP协议的套接字(socket)编程 粘包现象 如何解决粘包现象(重要的是解决的思路) struct模块的使用(打包、解包) 今日内容详细 Socket抽象层&#x…...

js原型链以及实现继承的手段
1.原型链 其基本思想是利用原型让一个引用类型继承另一个引用类型的属性和方法。 简单回顾一下构造函数、原型和实例的关系:每个构造函数都有一个原型对象,原型对象都包含一个指向构造函数的指针,而实例都包含一个指向原型对象的内部指针。…...

jdk8u201版本cpu.load过高问题的排查和解决
文章目录 1、背景2、现象3、排查定位4、原因总结5、解决 1、背景 jdk8u45版本存在安全漏洞,性能问题。需要升级到8u201 2、现象 升级到201版本后,出现cpu.load过高 3、排查定位 使用压测工具压测时,cpu.load过高问题必现,确认…...
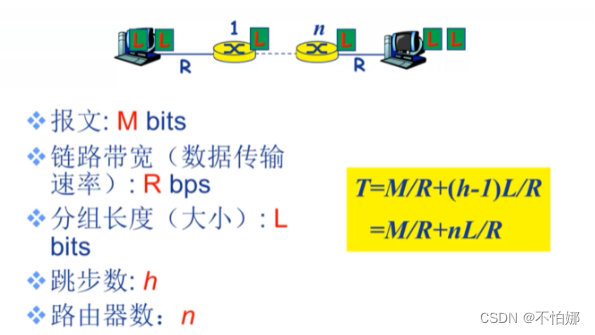
【计算机网络笔记】数据交换之报文交换和分组交换
系列文章目录报文交换分组交换存储-转发报文交换 vs 分组交换总结 系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 报文交换 报文:源(应用)发送的信息整体。比如一个文件、一…...

【广州华锐互动】利用VR开展细胞基础实验教学有什么好处?
在科技发展的驱动下,虚拟现实(VR)技术已被广泛应用于各个领域,包括教育和医学。尤其是在医学教育中,VR技术已成为一种革新传统教学模式的有效工具。本文将探讨使用VR进行细胞基础实验教学的优势。 首先,VR技…...
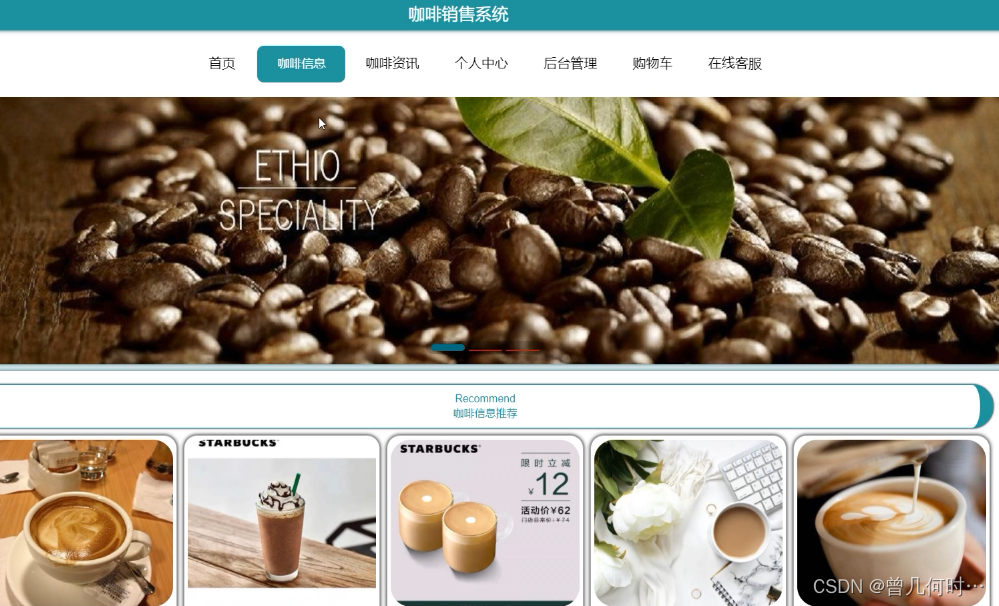
基于SSM+Vue的咖啡销售系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

L2-026 小字辈
本题给定一个庞大家族的家谱,要请你给出最小一辈的名单。 输入格式: 输入在第一行给出家族人口总数 N(不超过 100 000 的正整数) —— 简单起见,我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号,…...

linux 查看系统版本
命令:lsb_release -a 可能遇到的问题: 问题1: 报错:command not found: lsb_release原因:系统没有安装 lsb_release解决方案:sudo apt-get install lsb-release 问题2: 报错: Tra…...
Python实现PDF转换文件格式
最近工作中经常遇到收到其他人提供的pdf文档,想要编辑修改下或者复制部分内容比较困难,想通过现有的pdf工具软件转换文档格式,基本都要充钱,为了免费实现pdf转换工具,网上查了下相关技术方案,整理了下代码&…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
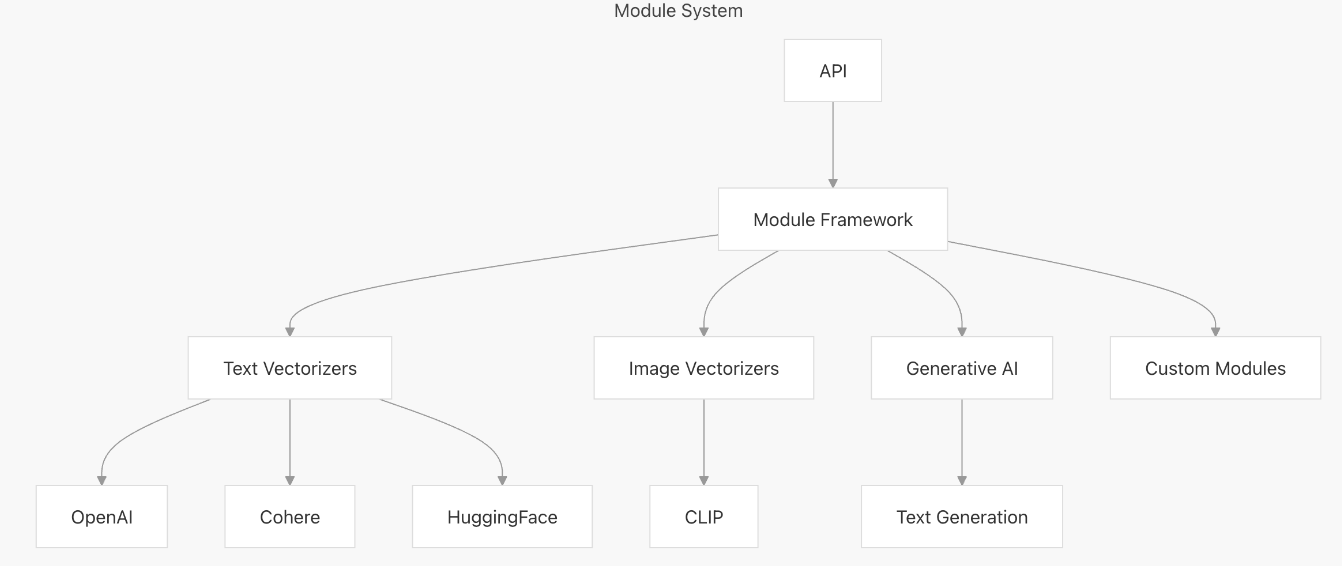
【向量库】Weaviate概述与架构解析
文章目录 一、什么是weaviate二、High-Level Architecture1. Core Components2. Storage Layer3. 组件交互流程 三、核心组件1. API Layer2. Schema Management3. Vector Indexing3.1. 查询原理3.2. 左侧:Search Process(搜索流程)3.3. 右侧&…...
进行稀疏数据预测的技术方案)
结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案
以下是一个结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案,包含完整数学推导、PyTorch/TensorFlow双框架实现代码及对比实验分析。 基于PINN的反应扩散方程稀疏数据预测与大规模数据泛化能力研究 1. 问题定义与数学模型 1.1 反应扩散方程 考虑标…...
