BZOJ2142 礼物
题目描述
一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物,当然他也会送出许多礼物。不同的人物在小E 心目中的重要性不同,在小E心中分量越重的人,收到的礼物会越多。小E从商店中购买了n件礼物,打算送给m个人 ,其中送给第i个人礼物数量为wi。请你帮忙计算出送礼物的方案数(两个方案被认为是不同的,当且仅当存在某 个人在这两种方案中收到的礼物不同)。由于方案数可能会很大,你只需要输出模P后的结果。
输入格式
输入的第一行包含一个正整数P,表示模; 第二行包含两个整整数n和m,分别表示小E从商店购买的礼物数和接受礼物的人数; 以下m行每行仅包含一个正整数wi,表示小E要送给第i个人的礼物数量。
输出格式
若不存在可行方案,则输出“Impossible”,否则输出一个整数,表示模P后的方案数。
输入样例
100
4 2
1
2输出样例
12
样例解释
下面是对样例1的说明。 以“/”分割,“/”前后分别表示送给第一个人和第二个人的礼物编号。12种方案详情如下: 1/23 1/24 1/34 2/13 2/14 2/34 3/12 3/14 3/24 4/12 4/13 4/23
数据范围
设P=p1c1×p2c2⋯×ptctP=p_1^{c_1}\times p_2^{c_2}\dots\times p_t^{c_t}P=p1c1×p2c2⋯×ptct,pip_ipi为质数。
对于100%100\%100%的数据,1≤n≤109,1≤m≤5,1≤pici≤1051\leq n\leq 10^9,1\leq m\leq 5,1\leq p_i^{c_i}\leq 10^51≤n≤109,1≤m≤5,1≤pici≤105。
题解
前置知识:扩展lucas定理
题意即求Cna1×Cn−a1a2×⋯×Cn−a1−a2−⋯−am−1amC_n^{a_1}\times C_{n-a_1}^{a_2}\times \cdots \times C_{n-a_1-a_2-\dots -a_{m-1}}^{a_m}Cna1×Cn−a1a2×⋯×Cn−a1−a2−⋯−am−1am。
根据Cnm=n!m!(n−m)!C_n^m=\dfrac{n!}{m!(n-m)!}Cnm=m!(n−m)!n!,我们整理可以发现,上述式子等于
n!a1!×a2!×⋯×am!×(n−a1−a2−⋯−am)!\dfrac{n!}{a_1!\times a_2!\times \cdots\times a_m!\times (n-a_1-a_2-\dots-a_m)!}a1!×a2!×⋯×am!×(n−a1−a2−⋯−am)!n!
我们呢可以用扩展lucas定理。因为1≤m≤51\leq m\leq 51≤m≤5,所以并不需要求太多次阶乘的逆元,与普通的扩展lucas定理的时间复杂度差不了多少。
code
#include<bits/stdc++.h>
using namespace std;
int tot=0;
long long n,m,x,y,sum,ans,w[10],r[105],a[105];
long long mod;
long long mi(long long t,long long v){if(v==0) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void exgcd(long long c,long long d){if(d==0){x=1;y=0;return;}exgcd(d,c%d);long long t=x;x=y;y=t-c/d*y;
}
long long gt(long long v,long long p,long long q){if(!v) return 1;long long re=1;for(int i=1;i<=q;i++){if(i%p) re=re*i%q;}re=mi(re,v/q)%q;for(int i=1;i<=v%q;i++){if(i%p) re=re*i%q;}return re*gt(v/p,p,q)%q;
}
long long C(long long p,long long q){if(n<m) return 0;long long f[10],f1=gt(n,p,q),f2=gt(sum,p,q),vt=0,re;for(int i=1;i<=m;i++) f[i]=gt(w[i],p,q);for(long long i=p;i<=n;i*=p) vt+=n/i;for(long long i=p;i<=sum;i*=p) vt-=sum/i;for(int j=1;j<=m;j++){for(long long i=p;i<=w[j];i*=p) vt-=w[j]/i;}re=mi(p,vt)%q*f1%q*(mi(f2,q-q/p-1)%q)%q;for(int i=1;i<=m;i++){re=re*(mi(f[i],q-q/p-1)%q)%q;}return re;
}
int main()
{long long v;scanf("%lld%lld%lld",&mod,&n,&m);sum=n;for(int i=1;i<=m;i++){scanf("%d",&w[i]);sum-=w[i];}if(sum<0){printf("Impossible");return 0;}v=mod;for(long long i=2;i*i<=v;i++){if(v%i==0){r[++tot]=1;while(v%i==0){r[tot]*=i;v/=i;}a[tot]=C(i,r[tot]);}}if(v>1){r[++tot]=v;a[tot]=C(v,v);}v=mod;for(int i=1;i<=tot;i++){exgcd(v/r[i],r[i]);x=(x%r[i]+r[i])%r[i];ans=(ans+v/r[i]*a[i]*x%v)%v;}printf("%lld",ans);return 0;
}
相关文章:

BZOJ2142 礼物
题目描述 一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物,当然他也会送出许多礼物。不同的人物在小E 心目中的重要性不同,在小E心中分量越重的人,收到的礼物会越多。小E从商店中购买了n件礼物,打算送给m个人 &…...
MySQL高级第一讲
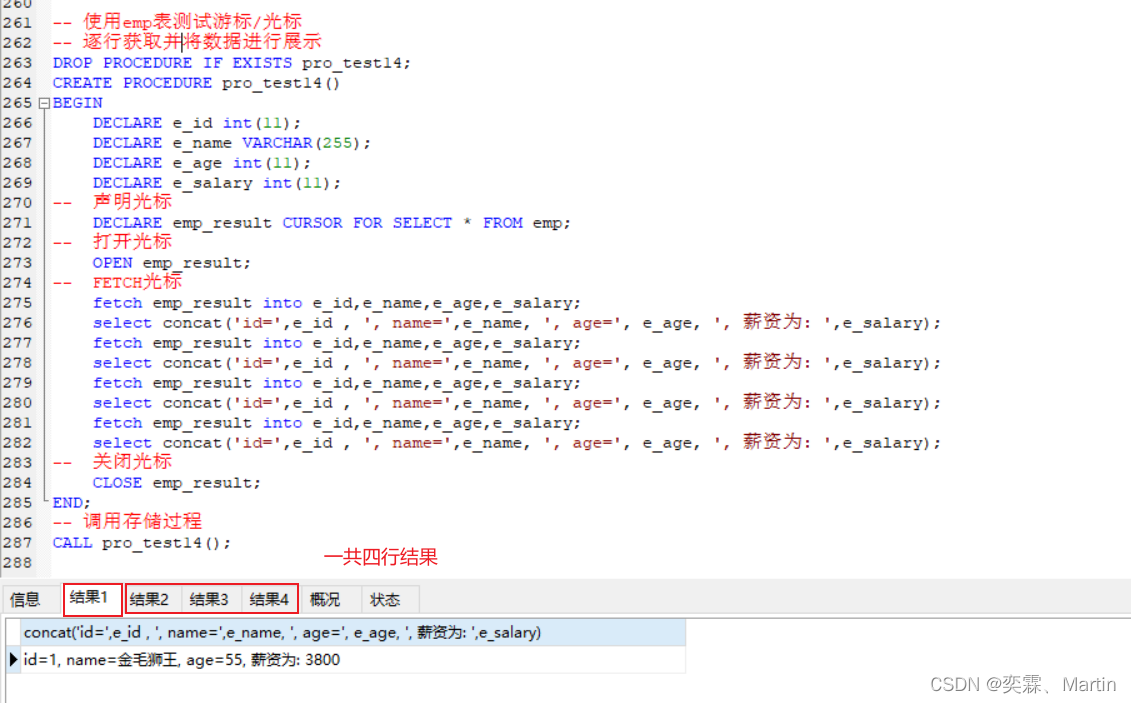
目录 一、MySQL高级01 1.1 索引 1.1.1 索引概述 1.1.2 索引特点 1.1.3 索引结构 1.1.4 BTREE结构(B树) 1.1.5 BTREE结构(B树) 1.1.6 索引分类 1.1.7 索引语法 1.1.8 索引设计原则 1.2 视图 1.2.1 视图概述 1.2.2 创建或修改视图 1.3 存储过程和函数 1.3.1 存储过…...

前端面试常用内容——基础积累
1.清除浮动的方式有哪些? 高度塌陷:当所有的子元素浮动的时候,且父元素没有设置高度,这时候父元素就会产生高度塌陷。 清除浮动的方式: 1.1 给父元素单独定义高度 优点: 快速简单,代码少 缺…...
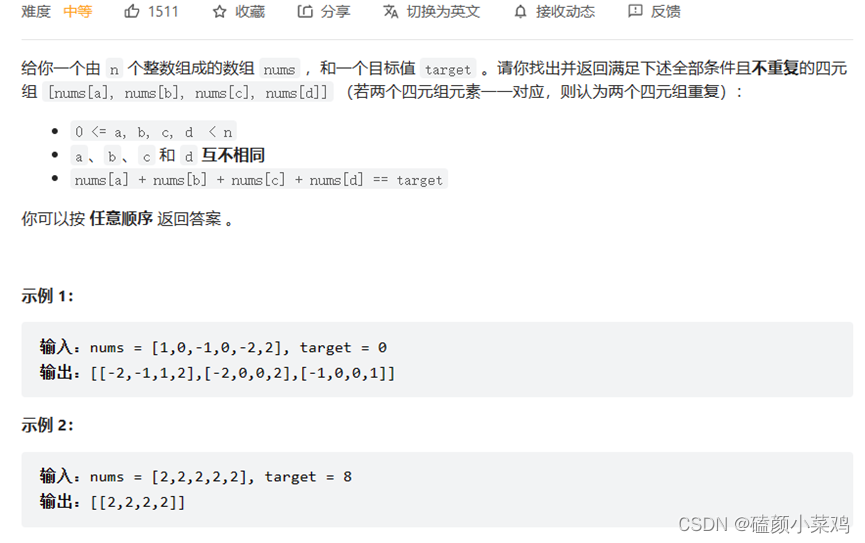
跟着《代码随想录》刷题(三)——哈希表
3.1 哈希表理论基础 哈希表理论基础 3.2 有效的字母异位词 242.有效的字母异位词 C bool isAnagram(char * s, char * t){int array[26] {0};int i 0;while (s[i]) {// 并不需要记住字符的ASCII码,只需要求出一个相对数值就可以了array[s[i] - a];i;}i 0;whi…...
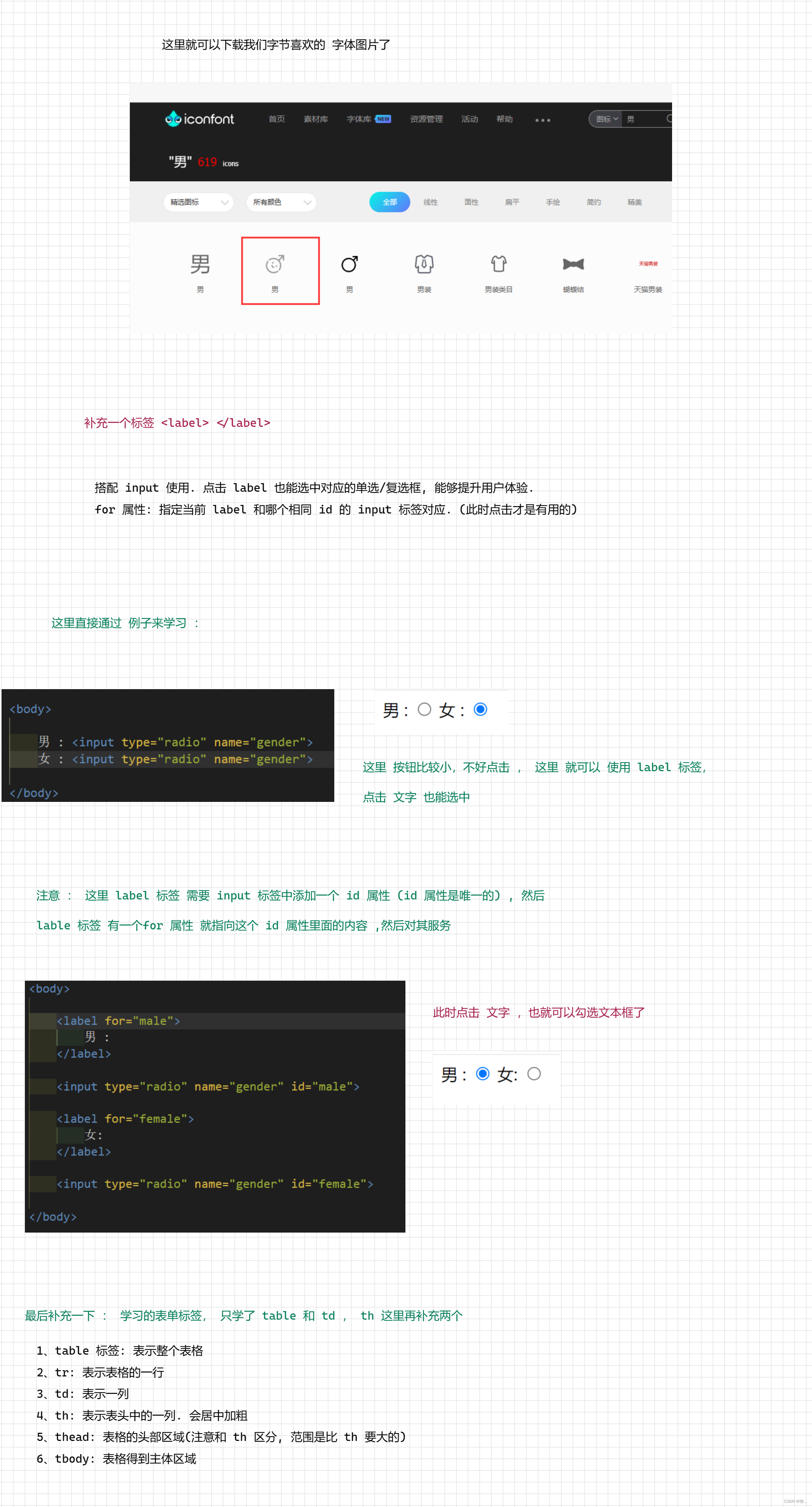
HTML - 扫盲
文章目录1. 前言2. HTML2.1 下载 vscode3 HTML 常见标签3.1 注释标签3.2 标题标签3.3 段落标签3.4 换行标签3.5 格式化标签1. 加粗2. 倾斜3. 下划线3.6 图片标签3.7 超链接标签3.8 表格标签3.9 列表标签4. 表单标签4.1 from 标签4.2 input 标签4.3 select 标签4.4 textarea标签…...
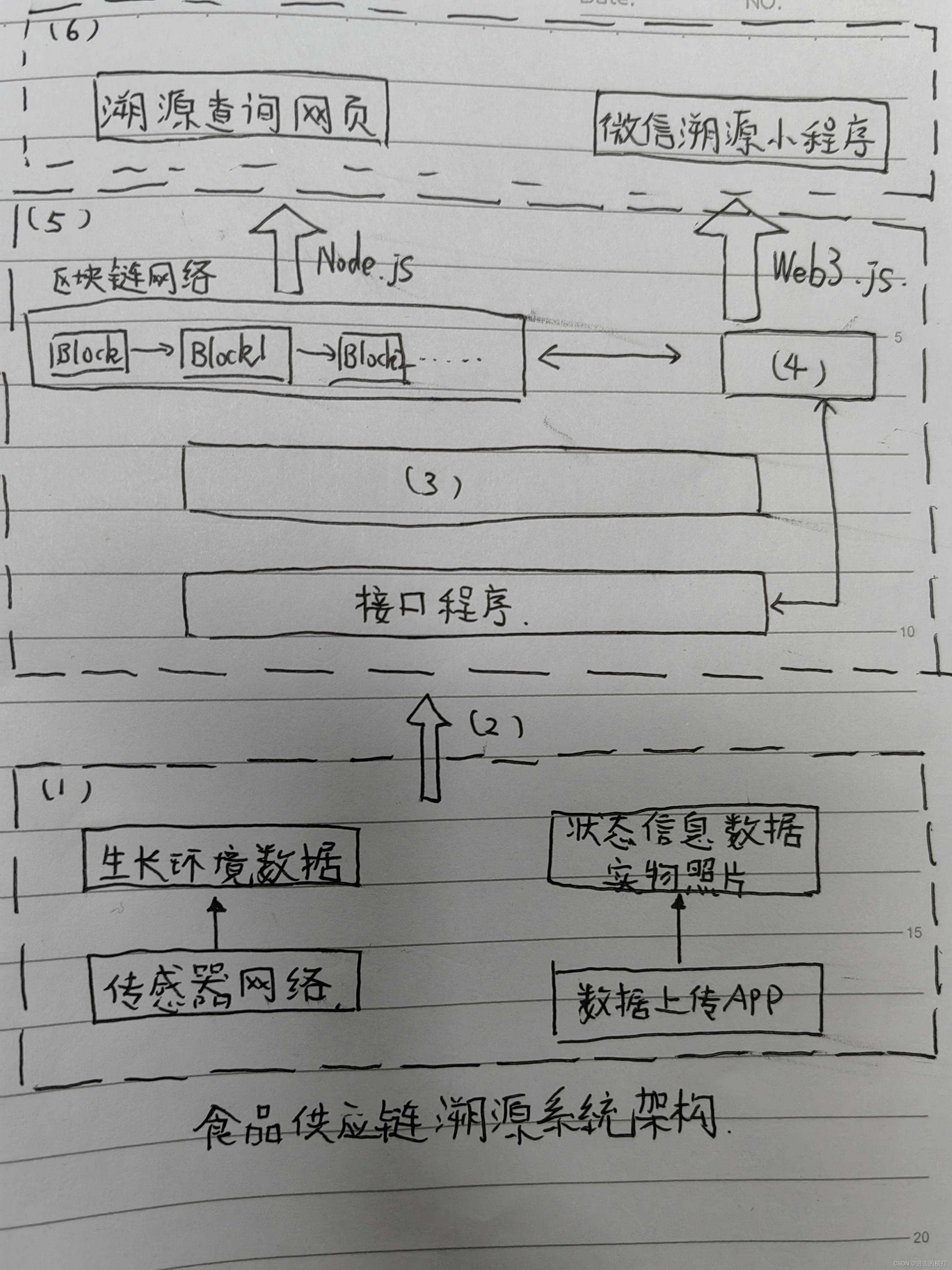
【系统分析师之路】2022上案例分析历年真题
【系统分析师之路】2022上案例分析历年真题 【系统分析师之路】2022上案例分析历年真题【系统分析师之路】2022上案例分析历年真题2022上案例分析历年真题第一题(25分)2022上案例分析历年真题第二题(25分)2022上案例分析历年真题第…...

Python编程规范
Python编程规范 当今Python编程社区有许多关于编程规范的约定和惯例。以下是一些常见的Python编程规范: 1.使用有意义的命名 使用有意义的命名可以使代码更加清晰、易读、易维护。变量、函数、类和模块的命名应该能够明确传达其用途,而不是使用无意义…...
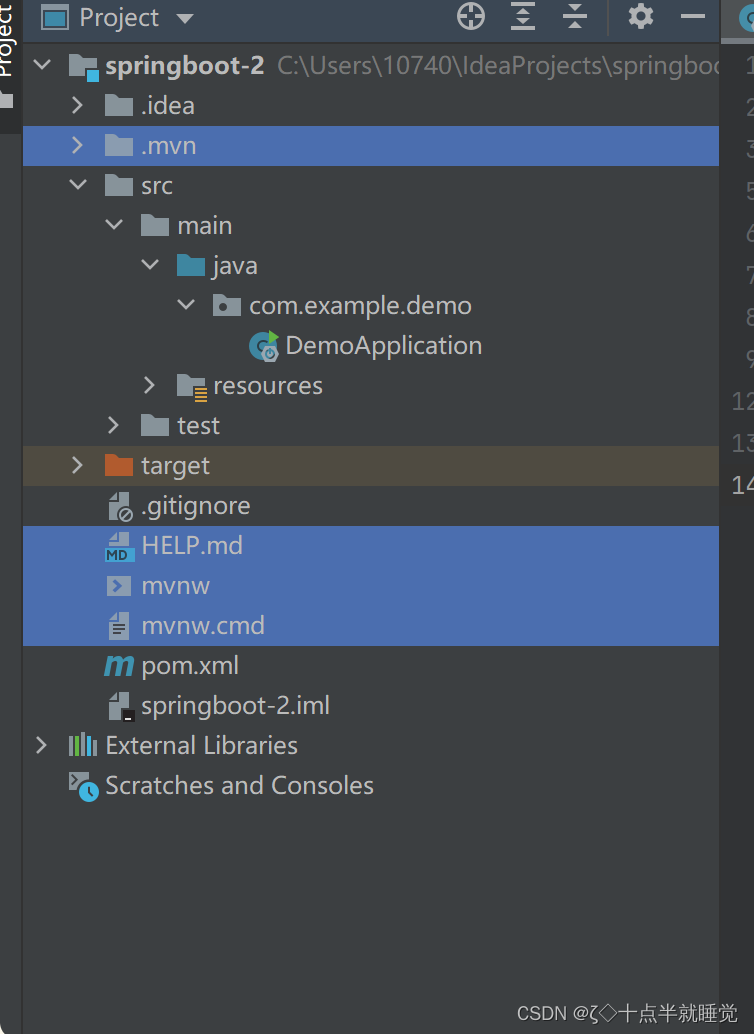
【Java】Spring Boot项目的创建和使用
文章目录SpringBoot的创建和使用1. 什么是Spring Boot?为什么要学Spring Boot?2. Spring Boot项目的优点3. Spring Boot 项目的创建3.1 使用idea创建3.2 接下来创建Spring Boot项目4. 项目目录介绍和运行4.1 运行项目4.2 输出内容5. 总结SpringBoot的创建…...
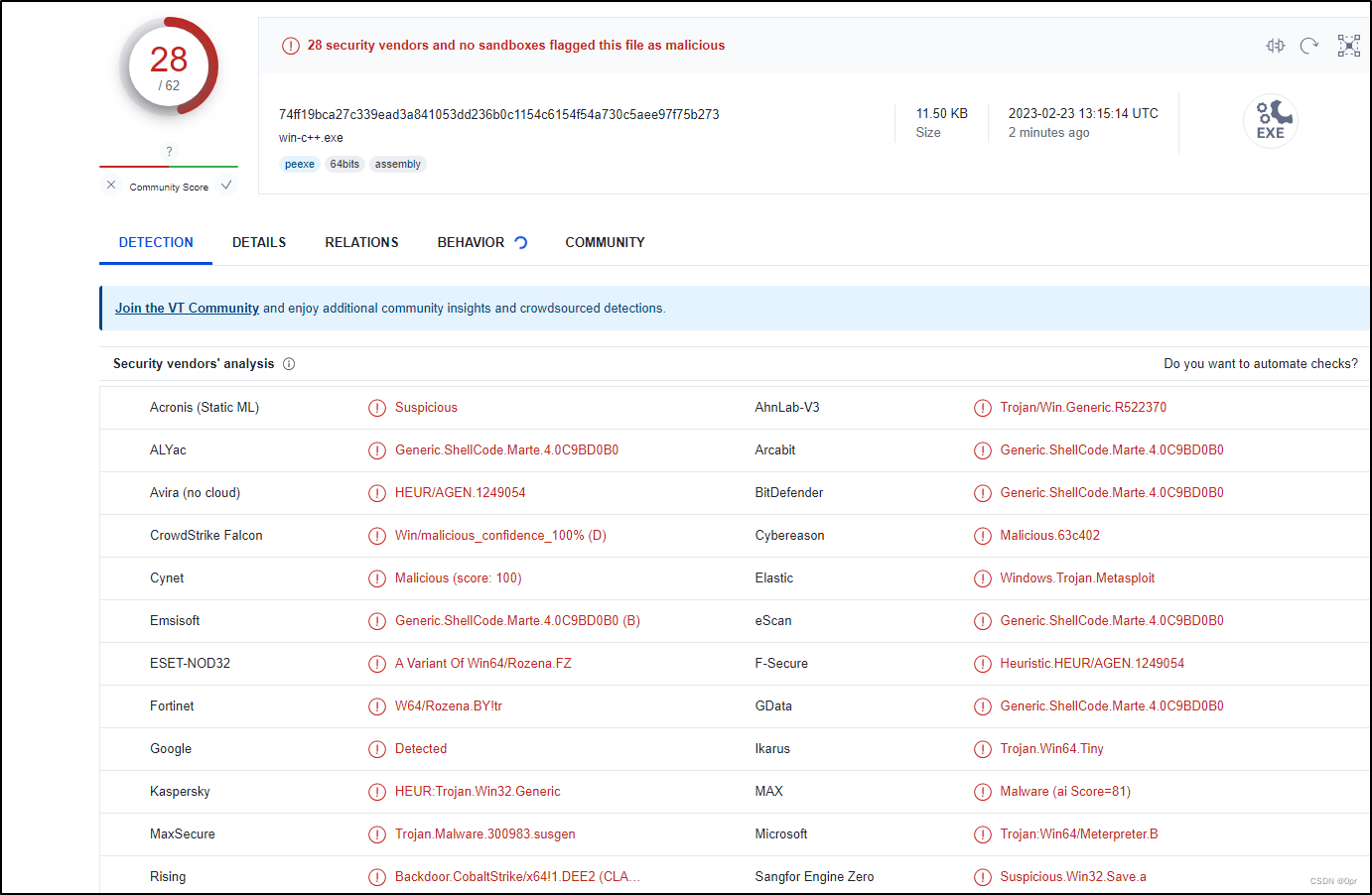
Malware Dev 00 - Rust vs C++ 初探
写在最前 如果你是信息安全爱好者,如果你想考一些证书来提升自己的能力,那么欢迎大家来我的 Discord 频道 Northern Bay。邀请链接在这里: https://discord.gg/9XvvuFq9Wb我会提供备考过程中尽可能多的帮助,并分享学习和实践过程…...

JavaScript HTML DOM 事件
文章目录JavaScript HTML DOM 事件对事件做出反应HTML 事件属性使用 HTML DOM 来分配事件onload 和 onunload 事件onchange 事件onmouseover 和 onmouseout 事件onmousedown、onmouseup 以及 onclick 事件JavaScript HTML DOM 事件 HTML DOM 使 JavaScript 有能力对 HTML 事件做…...
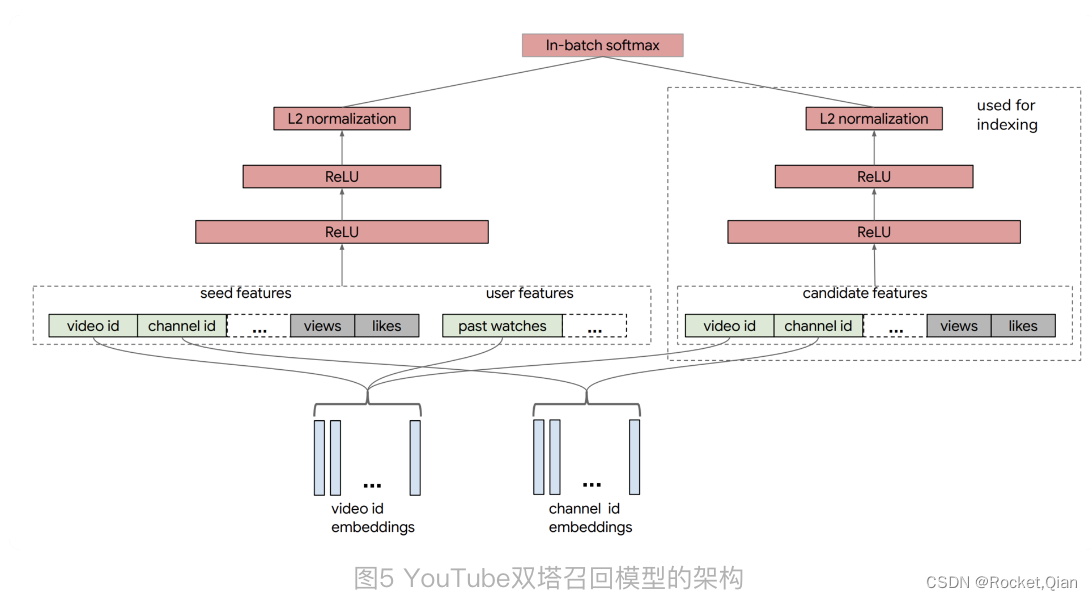
推荐算法——NCF知识总结代码实现
NCF知识总结代码实现1. NeuralCF 模型的结构1.1 回顾CF和MF1.2 NCF 模型结构1.3 NeuralCF 模型的扩展---双塔模型2. NCF代码实现2.1 tensorflow2.2 pytorchNeuralCF:如何用深度学习改造协同过滤? 随着技术的发展,协同过滤相比深度学习模型的…...

redis(4)String字符串
前言 Redis中有5大数据类型,分别是字符串String、列表List、集合Set、哈希Hash、有序集合Zset,本篇介绍Redis的字符串String Redis字符串 String是Redis最基本的类型,你可以理解成与Memcached一模一样的类型,一个key对应一个value…...

session一致性问题
在http访问请求中,web服务器会自动为同一个浏览器的访问用户自动创建唯一的session,提供数据存储功能。最常见的,会把用户的登录信息、用户信息存储在session中,以保持登录状态。只要用户不重启浏览器,每次http短连接请…...

上岸16K,薪资翻倍,在华为外包做测试是一种什么样的体验····
现在回过头看当初的决定,还是正确的,自己转行成功,现在进入了华为外包测试岗,脱离了工厂生活,薪资也翻了一倍不止。 我17年毕业于一个普通二本学校,电子信息工程学院,是一个很不出名的小本科。…...
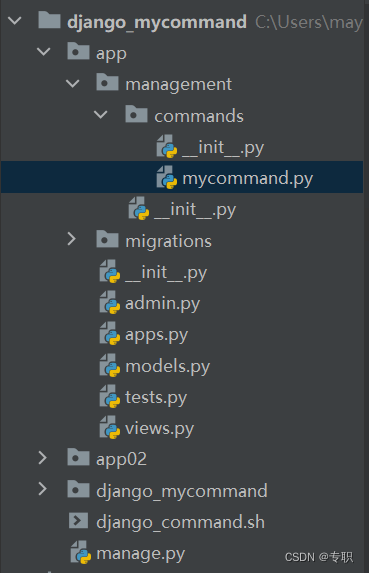
django项目中如何添加自定义的django command
项目目录 1.我们自己建立的application叫做app,首先在这个app目录下,我们需要新建management目录,这个目录里应该包括:__ init__.py(内容为空,用于打包)和commands目录,然后在comma…...

【算法基础】哈希表⭐⭐⭐
一、哈希表 散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。 给定表M,存在函数f(key),对任意…...

基于SpringMVC、Spring、MyBatis开发的校园点餐系统
文章目录 项目介绍主要功能截图:后台登录用户管理商品管理评论管理订单管理角色管理咨询管理前台前台首页我的订单商品详情支付方式选择支付成功页面部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题…...
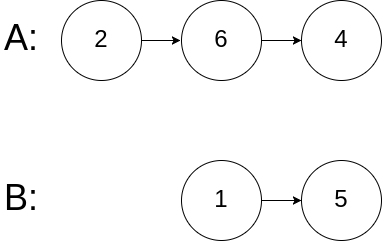
LeetCode 热题 C++ 148. 排序链表 152. 乘积最大子数组 160. 相交链表
力扣148 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 示例 1: 输入:head [4,2,1,3] 输出:[1,2,3,4]示例 2: 输入:head [-1,5,3,4,0] 输出:[-1,0,3,4,5]示例 3&#x…...

JavaScript 基础【快速掌握知识点】
目录 为什么要学JavaScript? 什么是JavaScript 特点: 组成: JavaScript的基本结构 基本结构 内部引用 外部引用 console对象进行输出 JavaScript核心语法 1、变量声明 2、数据类型 3、运算符 4、条件语句 5、循环语句 6、数组 7…...
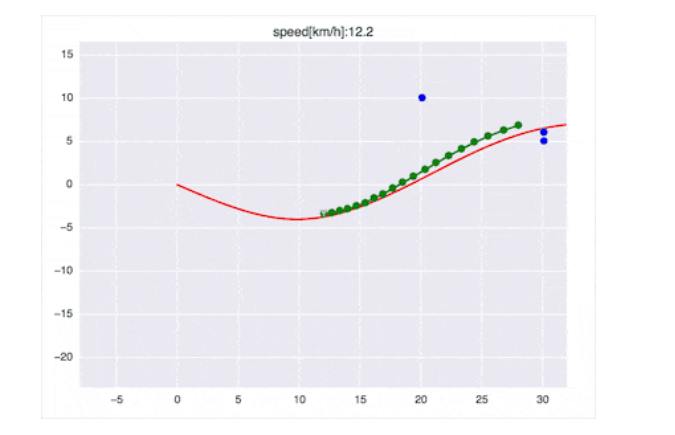
基于Frenet优化轨迹的⾃动驾驶动作规划⽅法
动作规划(Motion Control)在⾃动驾驶汽⻋规划模块的最底层,它负责根据当前配置和⽬标配置⽣成⼀序列的动作,本⽂介绍⼀种基于Frenet坐标系的优化轨迹动作规划⽅法,该⽅法在⾼速情况下的ACC辅助驾驶和⽆⼈驾驶都具有较强…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
