(三)代表性物质点邻域的变形分析
本文主要内容如下:
- 1. 伸长张量与Cauchy-Green 张量
- 2. 线元长度的改变
- 2.1. 初始/当前构型下的长度比
- 2.2. 主长度比与 Lagrange/Euler 主方向
- 2.3. 初始/当前构型下任意方向的长度比
- 3. 线元夹角的改变
- 4. 面元的改变
- 5. 体元的改变
1. 伸长张量与Cauchy-Green 张量
由于变形梯度为正则仿射量,故可进行极分解:
F=R⋅U=V⋅R\bold F=\bold R\cdot\bold U=\bold V\cdot \bold RF=R⋅U=V⋅R
将正交仿射量 R\bold RR 称作转动张量;正张量 U\bold UU、V\bold VV 分别称作 右、左伸长张量,且满足:
U=FT⋅FV=F⋅FTU=RT⋅V⋅R\bold U=\sqrt{\bold{F^T\cdot F}}\\\ \\ \bold V=\sqrt{\bold{F\cdot F^T}}\\\ \\ \bold U=\bold{R^T\cdot V\cdot R}U=FT⋅F V=F⋅FT U=RT⋅V⋅R
上述极分解的物理意义可以理解为:
dx⃗=F⋅dX⃗=R⋅(U⋅dX⃗)=V⋅(R⋅dX⃗)d\vec{x}=\bold F\cdot d\vec{X}=\bold R\cdot(\bold U\cdot d\vec{X})=\bold V\cdot(\bold R\cdot d\vec{X})dx=F⋅dX=R⋅(U⋅dX)=V⋅(R⋅dX)
即,参考构型的线元到当前构型中的线元的映射既可以是先进行旋转再进行左伸长仿射量对应的变换也可以是先进行右伸长张量对应的变换再进行旋转操作。
进一步可以定义:
C≜U2=FT⋅F=(C⃗A⊗G⃗A)T⋅(C⃗B⊗G⃗B)=CABG⃗A⊗G⃗B=(g⃗j⊗c⃗j)T⋅(g⃗i⊗c⃗i)=gjic⃗j⊗c⃗iB≜V2=F⋅FT=(g⃗i⊗c⃗i)⋅(g⃗j⊗c⃗j)T=c−1ijg⃗i⊗g⃗j≜c−1=(C⃗B⊗G⃗B)⋅(C⃗A⊗G⃗A)T=GBAC⃗B⊗C⃗A\begin{aligned} & \bold C\triangleq\bold U^2=\bold{F^T\cdot F}=(\vec{C}_A\otimes\vec{G}^A)^T\cdot(\vec{C}_B\otimes\vec{G}^B)=C_{AB}\vec{G}^A\otimes\vec{G}^B\\\\ &\qquad\qquad\qquad\quad\ \ =(\vec{g}_j\otimes\vec{c}\ ^j)^T\cdot(\vec{g}_i\otimes\vec{c}\ ^i)=g_{ji}\vec{c}\ ^j\otimes\vec{c}\ ^i\\\ \\ &\bold B\triangleq\bold V^2=\bold{F\cdot F^T}=(\vec{g}_i\otimes\vec{c}\ ^i)\cdot(\vec{g}_j\otimes\vec{c}\ ^j)^T=\overset{-1}{c}\ ^{ij}\vec{g}_i\otimes\vec{g}_j\triangleq\bold{\overset{-1}{c}}\\\\ &\qquad\qquad\qquad\quad\ \ =(\vec{C}_B\otimes\vec{G}^B)\cdot(\vec{C}_A\otimes\vec{G}^A)^T=G^{BA}\vec{C}_B\otimes\vec{C}_A \end{aligned} C≜U2=FT⋅F=(CA⊗GA)T⋅(CB⊗GB)=CABGA⊗GB =(gj⊗c j)T⋅(gi⊗c i)=gjic j⊗c iB≜V2=F⋅FT=(gi⊗c i)⋅(gj⊗c j)T=c−1 ijgi⊗gj≜c−1 =(CB⊗GB)⋅(CA⊗GA)T=GBACB⊗CA
C\bold CC 与 B\bold BB 分别称作右、左 Cauchy-Green 张量,二者间满足:
C=RT⋅B⋅R(正交相似关系)\bold{C}=\bold{R^T\cdot B\cdot R}\quad(正交相似关系)C=RT⋅B⋅R(正交相似关系)
说明,二者具有相同的特征值: λC=λB=λ\lambda_C=\lambda_B=\lambdaλC=λB=λ,特征方向仅相差一个刚性转动: u⃗C=RT⋅u⃗B\vec{u}_C=\bold{R}^T\cdot\vec{u}_BuC=RT⋅uB。另外,它们都是对称正定仿射量,是正则的,其逆分别为:
C−1=(U2)−1=F−1⋅F−T=(G⃗A⊗C⃗A)⋅(G⃗B⊗C⃗B)T=C−1ABG⃗A⊗G⃗B=(c⃗j⊗g⃗j)⋅(c⃗i⊗g⃗i)T=gjic⃗j⊗c⃗iB−1=(V2)−1=F−T⋅F−1=(c⃗i⊗g⃗i)T⋅(c⃗j⊗g⃗j)=cijg⃗i⊗g⃗j≜c=(G⃗A⊗C⃗A)T⋅(G⃗B⊗C⃗B)=GABC⃗A⊗C⃗B\begin{aligned} &\bold{\overset{-1}{C}}=(\bold U^2)^{-1}=\bold{\overset{-1}{F}\cdot \overset{-T}{F}}=(\vec{G}_A\otimes\vec{C}^A)\cdot(\vec{G}_B\otimes\vec{C}^B)^T=\overset{-1}{C}\ ^{AB}\vec G_A\otimes\vec G_B\\\ \\ &\qquad\qquad\qquad\qquad\quad \quad =(\vec c_j\otimes\vec{g}^j)\cdot(\vec c_i\otimes\vec{g}^i)^T=g^{ji}\vec c_j\otimes\vec c_i\\\\ &\bold{\overset{-1}{B}}=(\bold V^2)^{-1}=\bold{\overset{-T}{F}\cdot \overset{-1}{F}}=(\vec c_i\otimes\vec{g}^i)^T\cdot(\vec c_j\otimes\vec{g}^j)=c_{ij}\vec{g}^i\otimes\vec{g}^j\triangleq \bold c\\\\ &\qquad\qquad\qquad\quad\quad\quad\ \ =(\vec{G}_A\otimes\vec{C}^A)^T\cdot(\vec{G}_B\otimes\vec{C}^B)=G_{AB}\vec{C}^A\otimes\vec{C}^B \end{aligned} C−1=(U2)−1=F−1⋅F−T=(GA⊗CA)⋅(GB⊗CB)T=C−1 ABGA⊗GB=(cj⊗gj)⋅(ci⊗gi)T=gjicj⊗ciB−1=(V2)−1=F−T⋅F−1=(ci⊗gi)T⋅(cj⊗gj)=cijgi⊗gj≜c =(GA⊗CA)T⋅(GB⊗CB)=GABCA⊗CB
2. 线元长度的改变
2.1. 初始/当前构型下的长度比
设参考构型中 A 点邻域内的有向线元 dX⃗d\vec{X}dX 的长度为 ds0ds_0ds0;经过运动变形后,A 点映射为当前构型中的 A’ 点而 dX⃗d\vec{X}dX 映射为其邻域内的有向线元 dx⃗d\vec{x}dx ,长度为 dsdsds,满足:
{ds02=dX⃗⋅dX⃗=(dx⃗⋅F−T)⋅(F−1⋅dx⃗)=dx⃗⋅c⋅dx⃗=dx⃗⋅B−1⋅dx⃗ds2=dx⃗⋅dx⃗=(dX⃗⋅FT)⋅(F⋅dX⃗)=dX⃗⋅C⋅dX⃗\begin{cases} ds_0^2 =d\vec{X}\cdot d\vec{X} =(d\vec{x}\cdot\bold{\overset{-T}{F}})\cdot(\bold{\overset{-1}{F}}\cdot d\vec{x}) =d\vec{x}\cdot\bold{c}\cdot d\vec{x} =d\vec{x}\cdot\bold{\overset{-1}{B}}\cdot d\vec{x} \\\\ ds^2 =d\vec{x}\cdot d\vec{x} =(d\vec{X}\cdot\bold{F}^T)\cdot(\bold F\cdot d\vec{X}) =d\vec{X}\cdot\bold{C}\cdot d\vec{X} \end{cases}⎩⎨⎧ds02=dX⋅dX=(dx⋅F−T)⋅(F−1⋅dx)=dx⋅c⋅dx=dx⋅B−1⋅dxds2=dx⋅dx=(dX⋅FT)⋅(F⋅dX)=dX⋅C⋅dX
令
{L⃗≜dX⃗∣dX⃗∣=LiG⃗il⃗≜dx⃗∣dx⃗∣=lig⃗i\begin{cases} \vec{L}\triangleq\dfrac{d\vec{X}}{|d\vec{X}|}=L^i\vec{G}_i \\\\ \vec{l}\triangleq\dfrac{d\vec{x}}{|d\vec{x}|}=l^i\vec{g}_i \end{cases}⎩⎨⎧L≜∣dX∣dX=LiGil≜∣dx∣dx=ligi
将 L⃗、l⃗\vec{L}、\vec{l}L、l 分别称作变形前任意有向线元 dX⃗d\vec{X}dX 与变形后任意有向线元 dx⃗d\vec{x}dx 的单位切向量。
将变形前位于 L⃗\vec{L}L 方向的线元历经变形、运动前后的长度比定义为:
λL≜dsds0=(dX⃗⋅C⋅dX⃗∣dX⃗∣⋅∣dX⃗∣)12=(L⃗⋅C⋅L⃗)12=(LALBCAB)12(物质坐标系下的分量)\lambda_{L}\triangleq\dfrac{ds}{ds_0} =\left(\dfrac{d\vec{X}\cdot\bold{C}\cdot d\vec{X}}{|d\vec{X}|\cdot|d\vec{X}|}\right)^{\frac{1}{2}} =(\vec{L}\cdot\bold{C}\cdot\vec{L})^{\frac{1}{2}} =(L^AL^BC_{AB})^{\frac{1}{2}}\ (物质坐标系下的分量)λL≜ds0ds=(∣dX∣⋅∣dX∣dX⋅C⋅dX)21=(L⋅C⋅L)21=(LALBCAB)21 (物质坐标系下的分量)
将变形后位于 l⃗\vec{l}l 方向的线元历经变形、运动前后的长度比定义为:
λl≜dsds0=(∣dx⃗∣⋅∣dx⃗∣dx⃗⋅c⋅dx⃗)12=(l⃗⋅c⋅l⃗)−12=(lrlscrs)−12(空间坐标系下的分量)\lambda_{l}\triangleq\dfrac{ds}{ds_0} =\left(\dfrac{|d\vec{x}|\cdot|d\vec{x}|}{d\vec{x}\cdot\bold{c}\cdot d\vec{x}}\right)^{\frac{1}{2}} =(\vec{l}\cdot\bold{c}\cdot\vec{l})^{-\frac{1}{2}} =(l^rl^sc_{rs})^{- \frac{1}{2}}\ (空间坐标系下的分量)λl≜ds0ds=(dx⋅c⋅dx∣dx∣⋅∣dx∣)21=(l⋅c⋅l)−21=(lrlscrs)−21 (空间坐标系下的分量)
显然,当变形前位于 L⃗\vec{L}L 方向的线元经历变形、运动后位于 l⃗\vec{l}l 方向时有:
λL=λl\lambda_{L}=\lambda_lλL=λl
2.2. 主长度比与 Lagrange/Euler 主方向
此外,根据其定义可知:长度比是一个与方向相关的物理量,针对于参考构型/当前构型中同一点而言,不同方向的长度比不同。自然地会问:什么方向上长度比最大?即求解如下带约束的极值问题:
{maxL⃗λL(L⃗)∣L⃗∣=1和{maxl⃗λl(l⃗)∣l⃗∣=1\begin{cases} \max\limits_{\vec{L}}\ \lambda_{L}(\vec{L}) \\\\ |\vec{L}_|=1 \end{cases} \quad 和 \quad \begin{cases} \max\limits_{\vec{l}}\ \lambda_{l}(\vec{l}) \\\\ |\vec{l}|=1 \end{cases}⎩⎨⎧Lmax λL(L)∣L∣=1和⎩⎨⎧lmax λl(l)∣l∣=1
注意到长度比恒为正,为简化计算,将上述极值问题等价于求解:
{maxL⃗λL2(L⃗)∣L⃗∣=1和{maxl⃗λl2(l⃗)∣l⃗∣=1\begin{cases} \max\limits_{\vec{L}}\ \lambda_{L}^2(\vec{L}) \\\\ |\vec{L}|=1 \end{cases} \quad 和 \quad \begin{cases} \max\limits_{\vec{l}}\ \lambda_{l}^2(\vec{l}) \\\\ |\vec{l}|=1 \end{cases}⎩⎨⎧Lmax λL2(L)∣L∣=1和⎩⎨⎧lmax λl2(l)∣l∣=1
以前一个极值问题的求解为例,采用 Lagrange 乘子法进行求解,使得问题化为如下无约束极值问题的必要条件:
{∂∂LM[LALBCAB−η(LALBGAB−1)]=0(M=1,2,3)LALBGAB−1=0\begin{cases} \dfrac{\partial }{\partial L^M}\left[L^AL^BC_{AB}-\eta(L^AL^BG_{AB}-1)\right]=0\ (M=1,2,3)\\\\ L^AL^BG_{AB}-1=0 \end{cases}⎩⎨⎧∂LM∂[LALBCAB−η(LALBGAB−1)]=0 (M=1,2,3)LALBGAB−1=0
即
{(CAM−ηGAM)LA=0(M=1,2,3)LALBGAB−1=0⟹{(C∙MA−ηδ∙MA)LA=0(M=1,2,3)LALBGAB−1=0\begin{cases} (C_{AM}-\eta G_{AM})L^A=0\ (M=1,2,3)\\\\ L^AL^BG_{AB}-1=0 \end{cases} \Longrightarrow \begin{cases} (C^A_{\bullet M}-\eta \delta^A_{\bullet M})L_A=0\ (M=1,2,3)\\\\ L^AL^BG_{AB}-1=0 \end{cases}⎩⎨⎧(CAM−ηGAM)LA=0 (M=1,2,3)LALBGAB−1=0⟹⎩⎨⎧(C∙MA−ηδ∙MA)LA=0 (M=1,2,3)LALBGAB−1=0
注意到:CABC_{AB}CAB 不仅是右 Cauchy-Green 张量在物质坐标系下的协变分量,同时也是随体坐标系 {XA,t}\{X^A,t\}{XA,t} 度量张量的协变分量,但上述指标升降是通过物质坐标系下的度量张量协变、逆变分量实现的,因此 C∙MA≠δ∙MAC^A_{\bullet M}\ne\delta^A_{\bullet M}C∙MA=δ∙MA。
上述四元 非线性(约束条件) 方程组的求解等价于求右 Cauchy-Green 张量的特征值问题 :
(C−ηI)⋅L⃗=0(\bold C-\eta\bold I)\cdot\vec{L}=0(C−ηI)⋅L=0
由于 C\bold CC 为对称正定张量,故存在三个正特征值 ηα≜λα2>0(α=1,2,3)\eta_\alpha\triangleq\lambda_\alpha^2>0\ (\alpha=1,2,3)ηα≜λα2>0 (α=1,2,3) 和相应的三个两两垂直的单位特征向量 L⃗α\vec{L}_\alphaLα。
从上述讨论可知:于初始构型上的某点而言,该点右Cauchy-Green 张量 (右伸长张量 U) 的特征方向是该点变形、运动前后长度比达到极大/小或驻值的方向,将其称作 Lagrange 主方向。Lagrange 主方向上的长度比为:
λLα=L⃗α⋅C⋅L⃗α=λα2L⃗α⋅L⃗α=λα\lambda_{L_\alpha} =\sqrt{\vec{L}_\alpha\cdot\bold{C}\cdot\vec{L}_\alpha} =\sqrt{\lambda_\alpha^2\vec{L}_\alpha\cdot\vec{L}_\alpha} =\lambda_\alphaλLα=Lα⋅C⋅Lα=λα2Lα⋅Lα=λα
即,Lagrange 主方向上的长度比为该右Cauchy-Green 张量 C 特征方向对应特征值的算数平方根(右伸长张量 U 的特征值),将其称作 主长度比。
同理,求解后一极值问题等价于求解左 Cauchy-Green 张量的逆 c\bold cc 的特征值问题:
(c−η′I)⋅l⃗=0(\bold c-\eta'\bold I)\cdot\vec{l}=0(c−η′I)⋅l=0
其中,g\bold gg 为空间坐标系的度量张量。类似的,c\bold cc 也存在三个正特征值 ηα′≜1λα′2>0(α=1,2,3)\eta'_\alpha\triangleq\dfrac{1}{{\lambda'_\alpha}^2}>0\ (\alpha=1,2,3)ηα′≜λα′21>0 (α=1,2,3)和相应的三个两两垂直的单位特征向量 l⃗α\vec{l}_\alphalα。由于左、右 Cauchy-Green 张量具有相同的特征值,故
ηα′=1ηα=1λα2\eta'_\alpha=\dfrac{1}{\eta_\alpha}=\dfrac{1}{{\lambda_\alpha}^2}ηα′=ηα1=λα21
又由于左、右 Cauchy-Green 张量的特征方向仅相差一转动张量 R\bold RR,且正则仿射量与其逆同特征方向,则
L⃗α=RT⋅l⃗α(∗)\vec{L}_\alpha=\bold R^T\cdot\vec{l}_{\alpha}\quad(*)Lα=RT⋅lα(∗)
上述讨论说明对于当前构型上的某点,其左Cauchy-Green 张量或其逆 (或左伸长张量 V) 的特征方向是该点变形、运动前后长度比达到极大/小或驻值的方向,将其称作 Euler 主方向。Euler 主方向上的长度比为:
λlα=1l⃗α⋅c⋅l⃗α=λαl⃗α⋅l⃗α=λα\lambda_{l_\alpha} =\dfrac{1}{\sqrt{\vec{l}_\alpha\cdot\bold{c}\cdot\vec{l}_\alpha}} =\dfrac{\lambda_\alpha}{\sqrt{\vec{l}_\alpha\cdot\vec{l}_\alpha}} =\lambda_\alphaλlα=lα⋅c⋅lα1=lα⋅lαλα=λα
即,Euler 主方向上的长度比为该左Cauchy-Green 张量 B 特征方向对应的特征值的算数平方根 (左伸长张量 V 的特征值)。且 Euler 主方向上的长度比与 Lagrange 主方向上的长度比 分别一 一对应相等,即 λLα=λlα=λα\lambda_{L_\alpha}=\lambda_{l_\alpha}=\lambda_\alphaλLα=λlα=λα。
2.3. 初始/当前构型下任意方向的长度比
根据谱分解,左、右伸长张量,左、右 Cauchy-Green 张量,变形梯度张量及其逆可通过 Euler 主方向/ Lagrange 主方向 与主长度比进行表示,即:
{U=∑α=13λαL⃗α⊗L⃗αV=∑α=13λαl⃗α⊗l⃗α{C=∑α=13λα2L⃗α⊗L⃗αB=∑α=13λα2l⃗α⊗l⃗α,c=B−1=∑α=131λα2l⃗α⊗l⃗α\begin{aligned} &\begin{cases} \bold U=\sum\limits_{\alpha=1}^3\lambda_\alpha\vec{L}_\alpha\otimes\vec{L}_\alpha \\\\ \bold V=\sum\limits_{\alpha=1}^3\lambda_\alpha\vec{l}_\alpha\otimes\vec{l}_\alpha \end{cases} \\\\ &\begin{cases} \bold C = \sum\limits_{\alpha=1}^3\lambda^2_\alpha\vec{L}_\alpha\otimes\vec{L}_\alpha \\\\ \bold B=\sum\limits_{\alpha=1}^3\lambda^2_\alpha\ \vec{l}_\alpha\otimes\vec{l}_\alpha, \bold c=\bold B^{-1}=\sum\limits_{\alpha=1}^3\dfrac{1}{\lambda^2_\alpha}\ \vec{l}_\alpha\otimes\vec{l}_\alpha \end{cases} \end{aligned}⎩⎨⎧U=α=1∑3λαLα⊗LαV=α=1∑3λαlα⊗lα⎩⎨⎧C=α=1∑3λα2Lα⊗LαB=α=1∑3λα2 lα⊗lα,c=B−1=α=1∑3λα21 lα⊗lα
由于,转动张量也可通过主方向进行表示
R=∑α=13l⃗α⊗L⃗α\bold R=\sum_{\alpha=1}^3\vec{l}_\alpha\otimes\vec{L}_\alphaR=α=1∑3lα⊗Lα
则有:
F=V⋅R=R⋅U=∑α=13λαl⃗α⊗L⃗αF−1=RT⋅V−1=U−1⋅RT=∑α=131λαL⃗α⊗l⃗α\bold F =\bold {V\cdot R} =\bold {R\cdot U} =\sum_{\alpha=1}^3\lambda_{\alpha}\vec{l}_\alpha\otimes\vec{L}_\alpha \\\ \\ \bold F^{-1} =\bold {R^T\cdot V^{-1}} =\bold {U^{-1}\cdot R^{T}} =\sum_{\alpha=1}^3\dfrac{1}{\lambda_{\alpha}}\vec{L}_\alpha\otimes\vec{l}_\alphaF=V⋅R=R⋅U=α=1∑3λαlα⊗Lα F−1=RT⋅V−1=U−1⋅RT=α=1∑3λα1Lα⊗lα
-
对于参考构型中某点具有任意单位切向量 M⃗=MαL⃗α\vec{M}=M^\alpha\vec{L}_\alphaM=MαLα 的有向线元而言,其伸长比为:
λM=(M⃗⋅C⋅M⃗)12=[∑α=13(MαL⃗α)⋅∑i=13(λi2L⃗i⊗L⃗i)⋅∑β=13(MβL⃗β)]12=[∑α=13(λαMα)2]12(不对α、β求和)\lambda_M =(\vec{M}\cdot\bold C\cdot\vec{M})^{\frac{1}{2}} =\left[\sum_{\alpha=1}^3(M^\alpha\vec{L}_\alpha )\cdot\sum\limits_{i=1}^3\left(\lambda^2_i\vec{L}_i\otimes\vec{L}_i\right)\cdot \sum_{\beta=1}^3(M^\beta\vec{L}_\beta )\right]^{\frac{1}{2}} =\left[\sum_{\alpha=1}^3(\lambda_\alpha M^\alpha)^2\right]^{\frac{1}{2}}(不对 \alpha 、\beta求和)λM=(M⋅C⋅M)21=α=1∑3(MαLα)⋅i=1∑3(λi2Li⊗Li)⋅β=1∑3(MβLβ)21=[α=1∑3(λαMα)2]21(不对α、β求和)
其中, MαM^\alphaMα 为参考构型下任意单位切向量 M⃗\vec{M}M 在 Lagrange主方向下 的分量。 -
对于当前构型中某点具有任意单位切向量 m⃗=mαl⃗α\vec{m}=m^\alpha\vec{l}_\alpham=mαlα 的有向线元而言,其伸长比为:
λm=(m⃗⋅c⋅m⃗)−12=[∑α=13(mαl⃗α)⋅∑i=13(1λi2l⃗i⊗l⃗i)⋅∑β=13(mβl⃗β)]−12=[∑α=13(mαλα)2]−12(不对α、β求和)\lambda_m =(\vec{m}\cdot\bold c\cdot\vec{m})^{-\frac{1}{2}} =\left[\sum_{\alpha=1}^3(m^\alpha\vec{l}_\alpha )\cdot \sum\limits_{i=1}^3\left(\dfrac{1}{\lambda^2_i}\ \vec{l}_i\otimes\vec{l}_i\right)\cdot \sum_{\beta=1}^3(m^\beta\vec{l}_\beta )\right]^{-\frac{1}{2}} =\left[\sum_{\alpha=1}^3\left(\dfrac{m^\alpha}{\lambda_\alpha}\right)^2\right]^{-\frac{1}{2}}(不对 \alpha 、\beta求和)λm=(m⋅c⋅m)−21=α=1∑3(mαlα)⋅i=1∑3(λi21 li⊗li)⋅β=1∑3(mβlβ)−21=[α=1∑3(λαmα)2]−21(不对α、β求和)
其中, mαm^\alphamα 为当前构型下任意单位切向量 m⃗\vec{m}m 在 Euler主方向下 的分量。
3. 线元夹角的改变
下图为变形前后两线元的夹角变化过程:
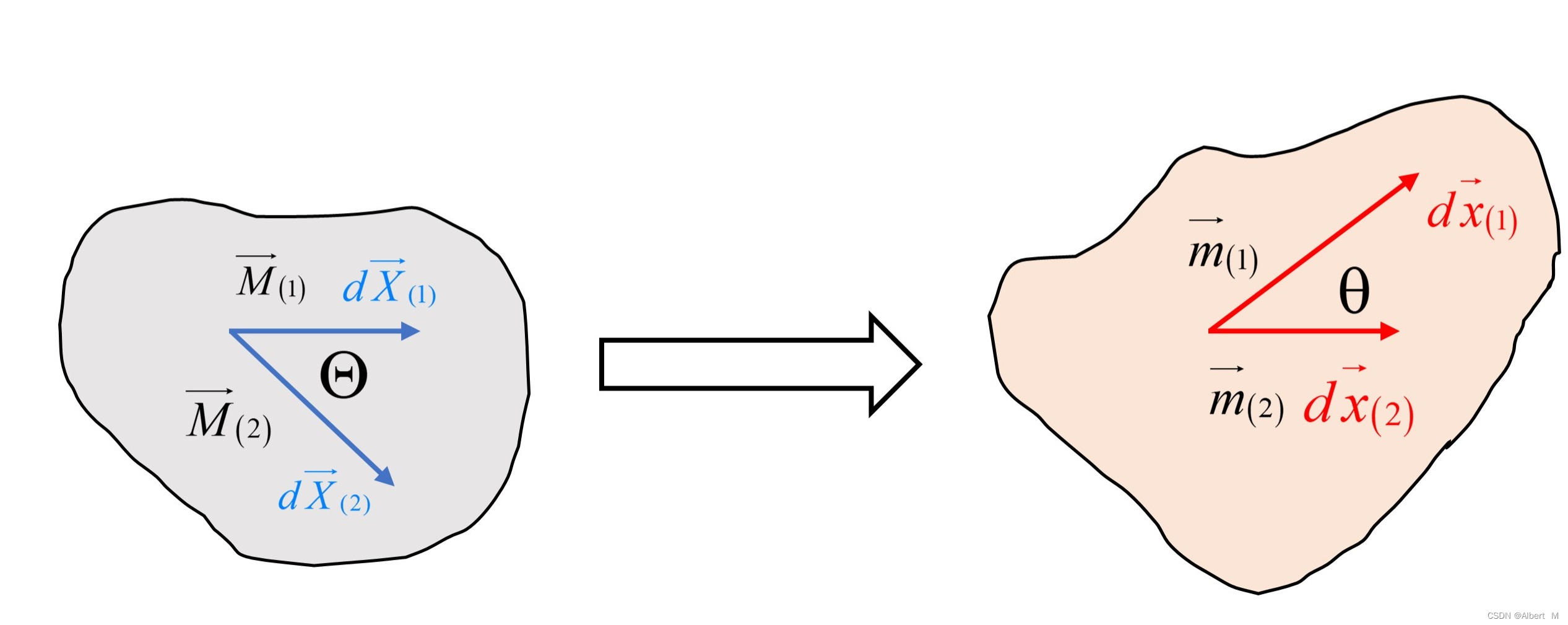
则变形前、后两线元的夹角余弦分别为:
cosΘ=M⃗(1)⋅M⃗(2)=dX⃗(1)⋅dX⃗(2)∣dX⃗(1)∣⋅∣dX⃗(2)∣cosθ=m⃗(1)⋅m⃗(2)=dx⃗(1)⋅dx⃗(2)∣dx⃗(1)∣⋅∣dx⃗(2)∣cos\Theta =\vec{M}_{(1)}\cdot\vec{M}_{(2)} =\dfrac{d\vec{X}_{(1)}\cdot d\vec{X}_{(2)}}{|d\vec{X}_{(1)}|\cdot|d\vec{X}_{(2)}|}\\\ \\ cos\theta =\vec{m}_{(1)}\cdot\vec{m}_{(2)} =\dfrac{d\vec{x}_{(1)}\cdot d\vec{x}_{(2)}}{|d\vec{x}_{(1)}|\cdot|d\vec{x}_{(2)}|}cosΘ=M(1)⋅M(2)=∣dX(1)∣⋅∣dX(2)∣dX(1)⋅dX(2) cosθ=m(1)⋅m(2)=∣dx(1)∣⋅∣dx(2)∣dx(1)⋅dx(2)
又
dx⃗(1)=F⋅dX⃗(1),dX⃗(1)=F−1⋅dx⃗(1)dx⃗(2)=F⋅dX⃗(2),dX⃗(2)=F−1⋅dx⃗(2)∣dx⃗(1)∣=λm(1)∣dX⃗(1)∣=λM(1)∣dX⃗(1)∣∣dx⃗(2)∣=λm(2)∣dX⃗(2)∣=λM(2)∣dX⃗(1)∣\begin{aligned} & d\vec{x}_{(1)}=\bold F\cdot d\vec{X}_{(1)},d\vec{X}_{(1)}=\bold{\overset{-1}{F}}\cdot d\vec{x}_{(1)} \\\\ & d\vec{x}_{(2)}=\bold F\cdot d\vec{X}_{(2)},d\vec{X}_{(2)}=\bold{\overset{-1}{F}}\cdot d\vec{x}_{(2)} \\\\ & |d\vec{x}_{(1)}|=\lambda_{m_{(1)}} |d\vec{X}_{(1)}|=\lambda_{M_{(1)}} |d\vec{X}_{(1)}| \\\\ & |d\vec{x}_{(2)}|=\lambda_{m_{(2)}} |d\vec{X}_{(2)}|=\lambda_{M_{(2)}} |d\vec{X}_{(1)}| \end{aligned}dx(1)=F⋅dX(1),dX(1)=F−1⋅dx(1)dx(2)=F⋅dX(2),dX(2)=F−1⋅dx(2)∣dx(1)∣=λm(1)∣dX(1)∣=λM(1)∣dX(1)∣∣dx(2)∣=λm(2)∣dX(2)∣=λM(2)∣dX(1)∣
-
那么,当立足于初始构型,若已知任意两方向,其夹角为 Θ\ThetaΘ,那么经过变形后两方向的夹角余弦为:
cosθ=dx⃗(1)⋅dx⃗(2)∣dx⃗(1)∣⋅∣dx⃗(2)∣=1λM(1)λM(2)dX⃗(1)⋅C⋅dX⃗(2)∣dX⃗(1)∣∣dX⃗(2)∣=1λM(1)λM(2)(M⃗(1)⋅C⋅M⃗(2))cos\theta =\dfrac{d\vec{x}_{(1)}\cdot d\vec{x}_{(2)}}{|d\vec{x}_{(1)}|\cdot|d\vec{x}_{(2)}|} =\dfrac{1}{\lambda_{M_{(1)}} \lambda_{M_{(2)}}}\dfrac{d\vec{X}_{(1)}\cdot\bold C\cdot d\vec{X}_{(2)}}{|d\vec{X}_{(1)}| |d\vec{X}_{(2)}|} =\dfrac{1}{\lambda_{M_{(1)}} \lambda_{M_{(2)}}}(\vec{M}_{(1)}\cdot\bold C\cdot \vec{M}_{(2)})cosθ=∣dx(1)∣⋅∣dx(2)∣dx(1)⋅dx(2)=λM(1)λM(2)1∣dX(1)∣∣dX(2)∣dX(1)⋅C⋅dX(2)=λM(1)λM(2)1(M(1)⋅C⋅M(2))
进一步,
cosθ=1λM(1)λM(2)[∑α=13(M(1)αL⃗α)⋅∑i=13(λi2L⃗i⊗L⃗i)⋅∑β=13(M(2)βL⃗β)]=1λM(1)λM(2)∑α=13(λα2M(1)αM(2)α)cos\theta=\dfrac{1}{\lambda_{M_{(1)}} \lambda_{M_{(2)}}}\left[\sum_{\alpha=1}^3(M_{(1)}^\alpha\vec{L}_\alpha )\cdot\sum\limits_{i=1}^3\left(\lambda^2_i\vec{L}_i\otimes\vec{L}_i\right)\cdot \sum_{\beta=1}^3(M_{(2)}^\beta\vec{L}_\beta )\right] =\dfrac{1}{\lambda_{M_{(1)}} \lambda_{M_{(2)}}}\sum\limits_{\alpha=1}^3(\lambda_\alpha^2M_{(1)}^\alpha M_{(2)}^\alpha)cosθ=λM(1)λM(2)1α=1∑3(M(1)αLα)⋅i=1∑3(λi2Li⊗Li)⋅β=1∑3(M(2)βLβ)=λM(1)λM(2)1α=1∑3(λα2M(1)αM(2)α)
其中, M(1)α、M(2)αM^\alpha_{(1)}、M^\alpha_{(2)}M(1)α、M(2)α 为参考构型下两任意单位切向量 M⃗(1)、M⃗(2)\vec{M}_{(1)}、\vec{M}_{(2)}M(1)、M(2) 分别在 Lagrange主方向下 的分量,λα\lambda_\alphaλα 为主长度比。 -
另外,若立足于当前构型,若已知任意两方向,其夹角为 θ\thetaθ,那么经历变形前两方向的夹角余弦为:
cosΘ=dX⃗(1)⋅dX⃗(2)∣dX⃗(1)∣⋅∣dX⃗(2)∣=(λm(1)λm(2))dx⃗(1)⋅c⋅dx⃗(2)∣dx⃗(1)∣∣dx⃗(2)∣=(λm(1)λm(2))(m⃗(1)⋅c⋅m⃗(2))cos\Theta =\dfrac{d\vec{X}_{(1)}\cdot d\vec{X}_{(2)}}{|d\vec{X}_{(1)}|\cdot|d\vec{X}_{(2)}|} =(\lambda_{m_{(1)}} \lambda_{m_{(2)}})\dfrac{d\vec{x}_{(1)}\cdot\bold c\cdot d\vec{x}_{(2)}}{|d\vec{x}_{(1)}| |d\vec{x}_{(2)}|} =(\lambda_{m_{(1)}} \lambda_{m_{(2)}})(\vec{m}_{(1)}\cdot\bold c\cdot \vec{m}_{(2)})cosΘ=∣dX(1)∣⋅∣dX(2)∣dX(1)⋅dX(2)=(λm(1)λm(2))∣dx(1)∣∣dx(2)∣dx(1)⋅c⋅dx(2)=(λm(1)λm(2))(m(1)⋅c⋅m(2))
进一步,
cosΘ=λm(1)λm(2)[∑α=13(m(1)αl⃗α)⋅∑i=13(1λi2l⃗i⊗l⃗i)⋅∑β=13(m(2)βl⃗β)]=(λm(1)λm(2))∑α=13(1λα2m(1)αm(2)α)cos\Theta=\lambda_{m_{(1)}} \lambda_{m_{(2)}}\left[\sum_{\alpha=1}^3(m_{(1)}^\alpha\vec{l}_\alpha )\cdot\sum\limits_{i=1}^3\left(\dfrac{1}{\lambda^2_i}\vec{l}_i\otimes\vec{l}_i\right)\cdot \sum_{\beta=1}^3(m_{(2)}^\beta\vec{l}_\beta )\right] =(\lambda_{m_{(1)}} \lambda_{m_{(2)}})\sum\limits_{\alpha=1}^3\left(\dfrac{1}{\lambda_\alpha^2}m_{(1)}^\alpha m_{(2)}^\alpha\right)cosΘ=λm(1)λm(2)α=1∑3(m(1)αlα)⋅i=1∑3(λi21li⊗li)⋅β=1∑3(m(2)βlβ)=(λm(1)λm(2))α=1∑3(λα21m(1)αm(2)α)
其中, m(1)α、m(2)αm^\alpha_{(1)}、m^\alpha_{(2)}m(1)α、m(2)α 为参考构型下两任意单位切向量 m⃗(1)、m⃗(2)\vec{m}_{(1)}、\vec{m}_{(2)}m(1)、m(2) 分别在 Euler主方向下 的分量,λα\lambda_\alphaλα 为主长度比。
4. 面元的改变
面元可通过如下的向量给出它的几何特征,向量的方向代表面元的单位法向量,向量的模代表面元的大小。则参考构型与当前构型下的平行四边形面元分别为:
{0N⃗dS0=dX⃗(1)×dX⃗(2)N⃗dS=dx⃗(1)×dx⃗(2)\begin{cases} {_0}\vec{N}dS_0=d\vec{X}_{(1)}\times d\vec{X}_{(2)} \\\\ \vec{N}dS=d\vec{x}_{(1)}\times d\vec{x}_{(2)} \end{cases}⎩⎨⎧0NdS0=dX(1)×dX(2)NdS=dx(1)×dx(2)
其中,0N⃗、N⃗{_0}\vec{N}、\vec{N}0N、N 分别为变形前后面元的单位法向量,dS0、dSdS_0、dSdS0、dS 分别为变形前后面元的大小。
那么,根据 Nanson 公式:
N⃗dS=(F⋅dX⃗(1))×(F⋅dX⃗(2))=det(F)F−T⋅(dX⃗(1)×dX⃗(2))=JF−T⋅0N⃗dS0\vec{N}dS =(\bold F\cdot d\vec{X}_{(1)})\times (\bold F\cdot d\vec{X}_{(2)}) =det(\bold F)\bold{\overset{-T}{F}}\cdot(d\vec{X}_{(1)}\times d\vec{X}_{(2)}) =\mathscr{J}\bold{\overset{-T}{F}}\cdot{_0}\vec{N}dS_0NdS=(F⋅dX(1))×(F⋅dX(2))=det(F)F−T⋅(dX(1)×dX(2))=JF−T⋅0NdS0
由于任何形状的面元均可通过无穷多个平行四边形来近似,故上述针对平行四边形面元的变换关系对于任意形状的面元也成立。
5. 体元的改变
参考/当前构型中的平行六面体的微元的体积分别为:
{dv0=∣dX⃗1⋅(dX⃗2×dX⃗3)∣dv=∣dx⃗1⋅(dx⃗2×dx⃗3)∣\begin{cases} dv_0=|d\vec{X}_1\cdot(d\vec{X}_2\times d\vec{X}_3)| \\\\ dv =|d\vec{x}_1\cdot(d\vec{x}_2\times d\vec{x}_3)| \end{cases}⎩⎨⎧dv0=∣dX1⋅(dX2×dX3)∣dv=∣dx1⋅(dx2×dx3)∣
那么,
dv=∣dx⃗1⋅(dx⃗2×dx⃗3)∣=∣(F⋅dX⃗1)⋅[(F⋅dX⃗2)×(F⋅dX⃗3)]∣=∣det(F)∣∣dX⃗1⋅(dX⃗2×dX⃗3)∣=∣J∣dv0=Jdv0=∣det(R)∣∣det(U)∣dv0=(∏α=13λα)dv0\begin{aligned} & dv =|d\vec{x}_1\cdot(d\vec{x}_2\times d\vec{x}_3)| \\\\ &\quad=|(\bold F\cdot d\vec{X}_1)\cdot[(\bold F\cdot d\vec{X}_2)\times (\bold F\cdot d\vec{X}_3)]| \\\\ &\quad=|det(\bold F)|\ |d\vec{X}_1\cdot(d\vec{X}_2\times d\vec{X}_3)| \\\\ &\quad=|\mathscr{J}|\ dv_0 =\mathscr{J}\ dv_0\\\\ &\quad=|det(\bold R)||det(\bold U)|\ dv_0 \\\\ &\quad=\left(\prod_{\alpha=1}^3\lambda_\alpha\right)\ dv_0 \end{aligned}dv=∣dx1⋅(dx2×dx3)∣=∣(F⋅dX1)⋅[(F⋅dX2)×(F⋅dX3)]∣=∣det(F)∣ ∣dX1⋅(dX2×dX3)∣=∣J∣ dv0=J dv0=∣det(R)∣∣det(U)∣ dv0=(α=1∏3λα) dv0
其中,λα(α=1,2,3)\lambda_\alpha(\alpha=1,2,3)λα(α=1,2,3) 为主长度比
由于任意形状的体元可以用无穷个多个平行六面体的逼近,故上述平行六面体体元间的映射关系对于任意形状的体元也是成立的。
对于 等容变形 应有:
J=1\mathscr{J}=1J=1
因此,有时也将变形梯度分解为等容部分与体积部分的乘积,其中等容部分定义为
F^≜J−13F\bold{\hat F} \triangleq \mathscr{J}^{-\frac{1}{3}}\bold FF^≜J−31F
显然,
det(F^)=1det(\bold{\hat F})=1det(F^)=1
则,
F=F^⋅(J13G)\bold F=\bold{\hat F}\cdot(\mathscr{J}^{\frac{1}{3}}\bold G)F=F^⋅(J31G)
显然,体积部分 J13G\mathscr{J}^{\frac{1}{3}}\bold GJ31G 是球形张量(各向同性张量)。
相关文章:

(三)代表性物质点邻域的变形分析
本文主要内容如下:1. 伸长张量与Cauchy-Green 张量2. 线元长度的改变2.1. 初始/当前构型下的长度比2.2. 主长度比与 Lagrange/Euler 主方向2.3. 初始/当前构型下任意方向的长度比3. 线元夹角的改变4. 面元的改变5. 体元的改变1. 伸长张量与Cauchy-Green 张量 由于变…...
Stream操作流 练习
基础数据:Data AllArgsConstructor NoArgsConstructor public class User {private String name;private int age;private String sex;private String city;private Integer money; static List<User> users new ArrayList<>();public static void m…...

【模拟集成电路】宽摆幅压控振荡器(VCO)设计
鉴频鉴相器设计(Phase Frequency Detector,PFD)前言一、VCO工作原理二、VCO电路设计VCO原理图三、压控振荡器(VCO)测试VCO测试电路图瞬态测试(1)瞬态输出(2)局部放大图&a…...

《英雄编程体验课》第 13 课 | 双指针
文章目录 零、写在前面一、最长不重复子串1、初步分析2、朴素算法3、优化算法二、双指针1、算法定义2、算法描述3、条件1)单调性2)时效性三、双指针的应用1、前缀和问题2、哈希问题3、K 大数问题零、写在前面 该章节节选自 《夜深人静写算法》,主要讲解最基础的枚举算法 ——…...

DS期末复习卷(十)
一、选择题(24分) 1.下列程序段的时间复杂度为( A )。 i0,s0; while (s<n) {ssi;i;} (A) O(n^1/2) (B) O(n ^1/3) © O(n) (D) O(n ^2) 12…xn xn^1/2 2.设某链表中最常用的…...

QT+OpenGL模板测试和混合
QTOpenGL模板测试和混合 本篇完整工程见gitee:QtOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主 模板测试 当片段着色器处理完一个片段之后,模板测试会开始执行。和深度测试一样,它可能会丢弃片段&am…...

《英雄编程体验课》第 11 课 | 前缀和
文章目录 零、写在前面一、概念定义1、部分和2、朴素做法3、前缀和4、前缀和的边界值5、边界处理6、再看部分和二、题目描述1、定义2、求解三、算法详解四、源码剖析五、推荐专栏六、习题练习零、写在前面 该章节节选自 《算法零基础100讲》,主要讲解最基础的算法 —— 前缀和…...

Java学习--多线程2
2.线程同步 2.1卖票【应用】 案例需求 某电影院目前正在上映国产大片,共有100张票,而它有3个窗口卖票,请设计一个程序模拟该电影院卖票 实现步骤 定义一个类SellTicket实现Runnable接口,里面定义一个成员变量:privat…...
【Virtualization】Windows11安装VMware Workstation后异常处置
安装环境 Windows 11 专业版 22H2 build 22621.1265 VMware Workstation 17 Pro 17.0.0 build-20800274 存在问题 原因分析 1、BIOS未开启虚拟化。 2、操作系统启用的虚拟化与Workstation冲突。 3、操作系统启用内核隔离-内存完整性保护。 处置思路 1、打开“资源管理器”…...
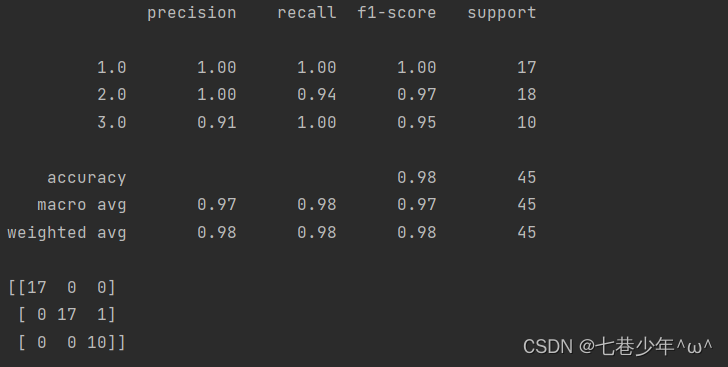
第四章.神经网络—BP神经网络
第四章.神经网络 4.3 BP神经网络 BP神经网络(误差反向传播算法)是整个人工神经网络体系中的精华,广泛应用于分类识别,逼近,回归,压缩等领域,在实际应用中,大约80%的神经网络模型都采用BP网络或BP网络的变化…...
如何压缩RAR格式文件?
RAR是我们日常生活工作中经常用到的压缩文件格式之一,那么RAR文件如何压缩呢? 不管压缩哪种格式的压缩文件,我们都需要用到压缩软件。针对RAR格式,我们可以选择最常见的WinRAR,当然如果有同样适用于RAR格式的压缩软件…...
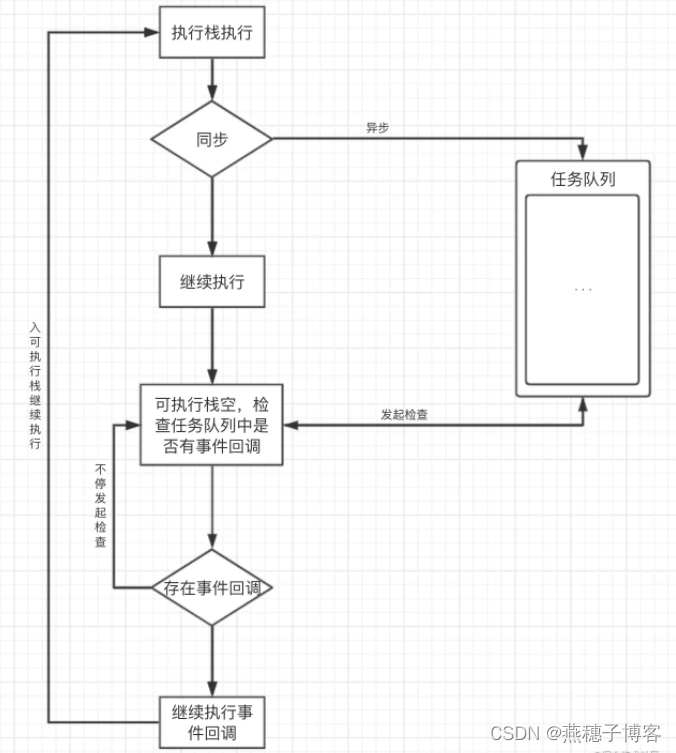
JS 执行机制 详解(附图)
一、JS是单线程JS语言的一大特点就是单线程,也就是说,同一个时间只能做一件事。这是JS这门脚本语言诞生的使命所致——用来处理页面中用户的交互,以及操作DOM而诞生的。单线程就意味着,所有任务需要排队,前一个任务结束…...
)
华为OD机试真题Java实现【 计算面积】真题+解题思路+代码(20222023)
计算面积 绘图机器的绘图笔初始位i在原点(0.0)。 机器启动后其绘图笔按下面规则绘制直线: 1 )尝试沿着横向坐标轴正向绘制直线,直到给定的终点值E, 2 )期间可通过指令在纵坐标轴方向进行偏移。井同时绘制直线,偏移后按规则1绘制直线;指令的格式为X offsetY。表示在横坐标X…...
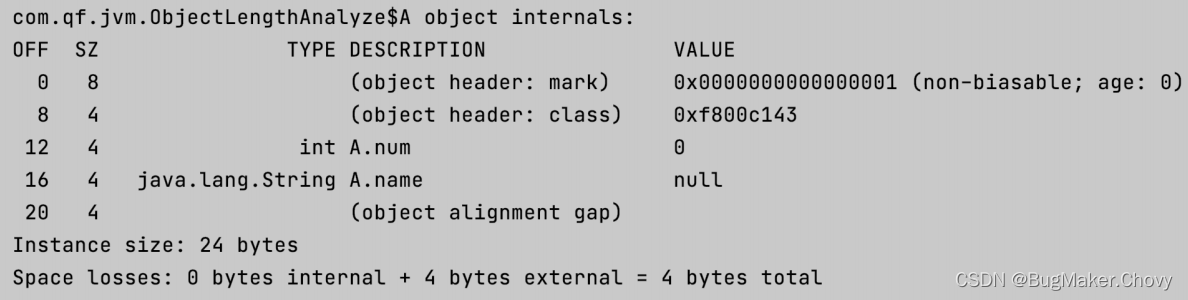
【JVM】运行时数据区与对象的创建流程
4、运行时数据区 4.1、运行时数据区介绍 运行时数据区也就是JVM在运⾏时产生的数据存放的区域,这块区域就是JVM的内存区域,也称为JVM的内存模型——JMM 堆空间(线程共享):存放new出来的对象 元空间(线程共…...
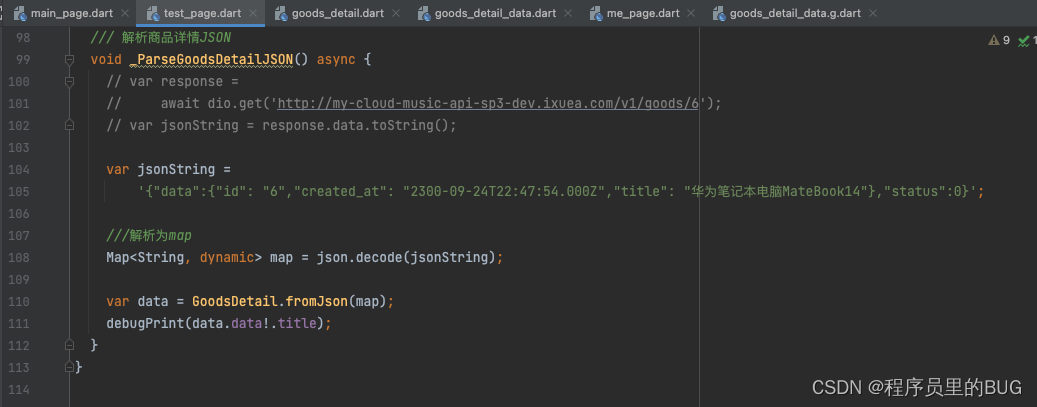
flutter- JSON解析框架使用方法json_serializable
对于目前来说,大部分的API网络请求的通讯内容数据格式都是JSON。JSON返回的都是字符串,假如要取到data里面的id,去直接字符串截取肯定是不行的,要通过一定的方式把它解析成Map或者解析成对象,再去处理它。像一些简单的…...
第十三届蓝桥杯国赛 C++ B 组 J 题——搬砖(AC)
目录1.搬砖1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.搬砖 1.题目描述 这天,小明在搬砖。 他一共有 nnn 块砖, 他发现第 iii 砖的重量为 wiw_{i}wi, 价值为 viv_{i}vi 。他突然想从这些 砖中选一些出来从…...
- Nacos服务端服务发现处理)
Spring Cloud Nacos源码讲解(十)- Nacos服务端服务发现处理
Nacos集群数据同步 当我们有服务进行注册以后,会写入注册信息同时会触发ClientChangedEvent事件,通过这个事件,就会开始进行Nacos的集群数据同步,当然这其中只有有一个Nacos节点来处理对应的客户端请求,其实这其中…...
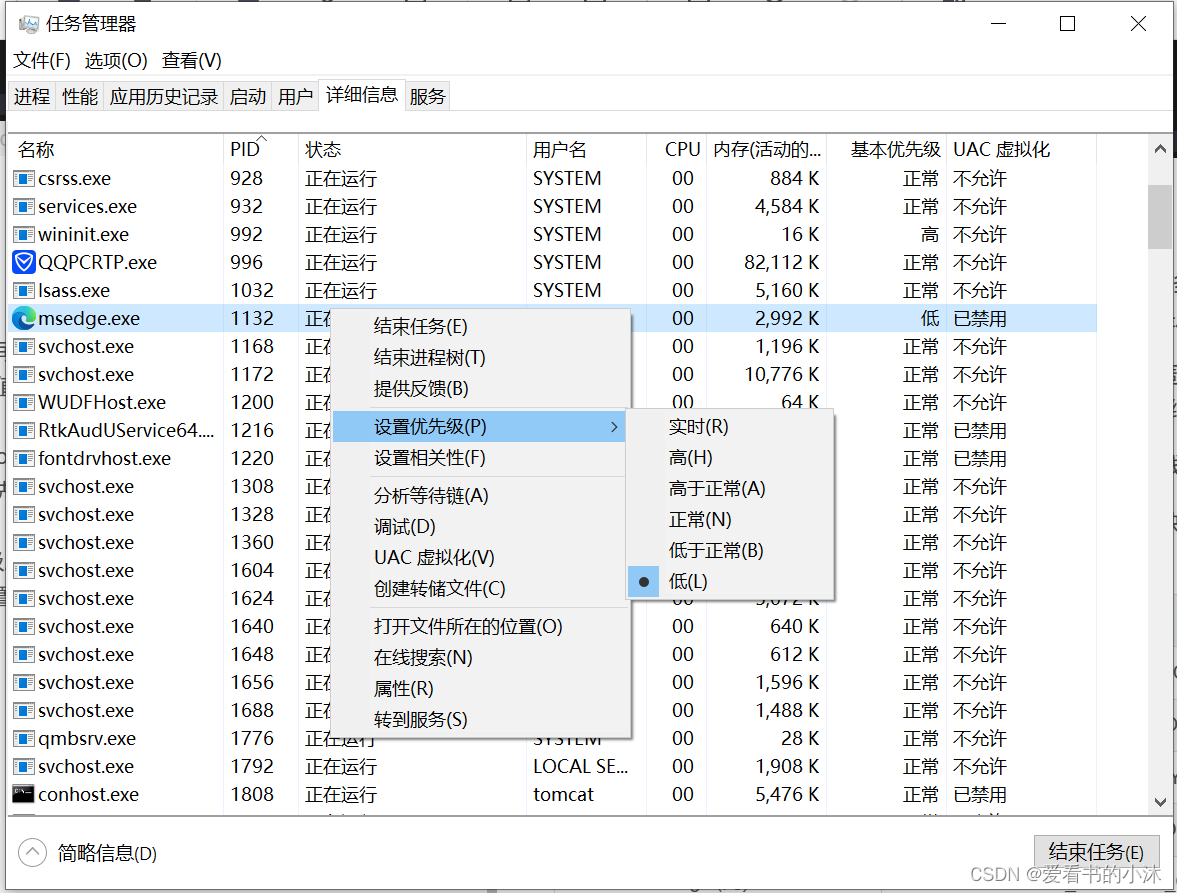
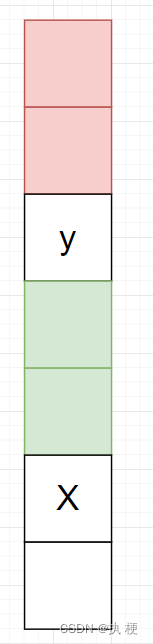
C++ 修改程序进程的优先级(Linux,Windows)
文章目录1、Linux1.1 常用命令1.1.1 不占用终端运行和后台运行方式1.1.2 查询进程1.1.3 结束进程1.1.4 优先级命令1.2 C 代码示例1.2.1 代码一1.2.2 代码二2、Windows2.1 简介2.2 函数声明2.3 C 代码示例2.3.1 代码一2.3.2 代码二结语1、Linux 1.1 常用命令 1.1.1 不占用终端…...
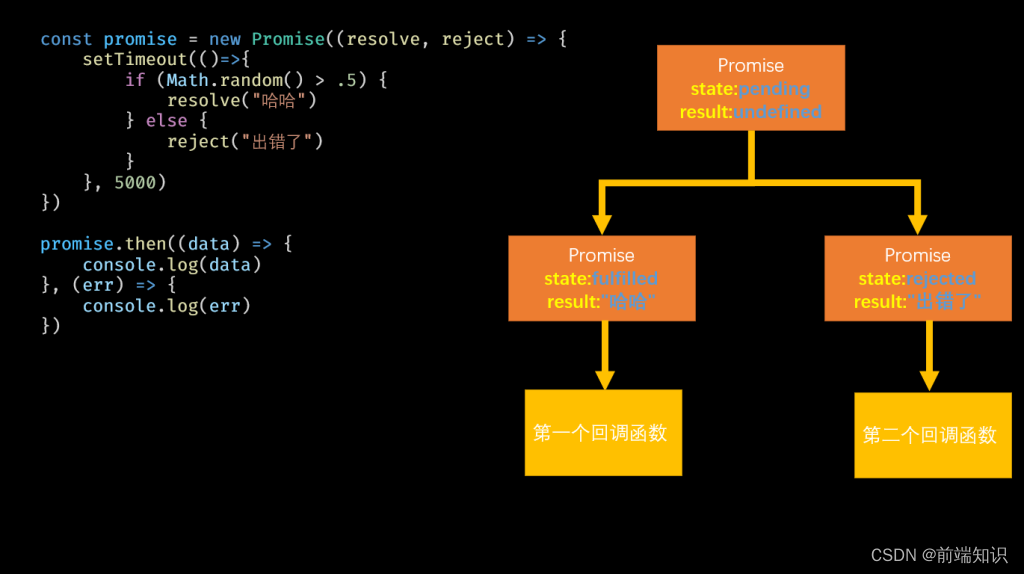
同步和异步promise
进程和线程进程(厂房):程序的运行环境线程(工人):进行运算的东西同步和异步同步:一件事干完才去干下一件事,前面的代码不执行,后面的代码也不执行。同步的代码可能会出现…...
CHATGPT是新的“搜索引擎终结者”吗?百度是否慌了
ChatGPT 以其非凡的自然语言处理 (NLP) 能力和清晰的响应风靡全球,有望带来一场重大的技术革命。在不知不觉中,叙事转向了ChatGPT与百度的对决,因为来自OpenAI的智能和健谈的聊天机器人已经慢慢获得了“潜在的百度终结…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
