Verilog 逻辑与()、按位与()、逻辑或(||)、按位或(|)、等于(==)、全等(===)的区别
逻辑与(&&)
逻辑与是一个双目运算符,当符号两边为1时输出1,符号两边为0时输出0。
真值表:
&& | 0 | 1 | x | z |
0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | x | x |
x | 0 | x | x | x |
z | 0 | x | x | x |
两个4bit的数字相与;A=4'b0x1z;B=4'b01xx;C=4'b00xz;求A&&B;A&&C;是什么值?当逻辑与&&操作符两边的数字均含有“1”,则输出1。
那么怎么判断A、B、C为是否含有“1”呢。当A为0的时候,A等于4'b0,即每位都为0,即只需A的4位矢量之间做一下“逻辑或”运算,A[3] || A[2] || A[1] || A[0],也可写成(|A);当4位矢量中只需有一位为1,那么A就含有“1”。即哪怕A中具有不定态x或者高阻态z,A = 4'b0x1z在逻辑与的判断下会判定为“1”。
故 A && B = 4'b0x1z && 4'b01xx = 1
C = 4'b00xz,其中没有bit位为1,所以在逻辑与的眼中,C为“1”,进而有:
A && C = 4'b0x1z && 4'b00xz = 0
按位与(&)
按位与有两种使用方式,一种是双目操作,即一个操作符对应两个操作数A&B;另一种是单目操作,即一个操作符对应一个操作数&A。
双目操作
一个4bit的数和一个4bit的数按位与的结果还是一个4bit数,例如A[3:0] & B[3:0] = { A[3] && B[3] , A[2] && B[2], A[1] && B[1], A[0] && B[0] }
假设A = 4'b10xz;B = 4'b0011;C = 4'bz011;
A & B = 4'b00xx;A & C =4'bx0xx;
单目操作
一个4bit的数对自己进行按位与,输出的结果为1bit的数。
假设A = 4'b10xz;B = 4'b0011;
& A = A[3] && A[2] && A[1] && A[0] = 0
& B = 0
因为4bit数A和B中间都有0,所以A、B按位与结果都为0。
若C = 4'b11xz;则 & C = x
逻辑或(||)
逻辑或是一个双目运算符,当符号两边有1时输出1,符号两边全0时输出0。
|| | 0 | 1 | x | z |
0 | 0 | 1 | x | x |
1 | 1 | 1 | 1 | 1 |
x | x | 1 | x | x |
z | x | 1 | x | x |
两个4bit的数字相与;A=4'b0x1z;B=4'b01xx;C=4'b00xz;求A&&B;A&&C;是什么值?当逻辑与&&操作符两边的有数字含有“1”,则输出1。
当4位矢量中只需有一位为1,那么A就含有“1”。即哪怕A中具有不定态x或者高阻态z,A = 4'b0x1z在逻辑与的判断下会判定为“1”。
所以A || B = 1;A || C = 1
按位或(|)
同按位与一样,按位或也有两种使用方式,一种是双目操作,即一个操作符对应两个操作数A|B;另一种是单目操作,即一个操作符对应一个操作数|A。
双目操作
一个4bit的数和一个4bit的数按位或的结果还是一个4bit数,例如A[3:0] & B[3:0] = { A[3] || B[3] , A[2] || B[2], A[1] || B[1], A[0] || B[0] }
假设A = 4'b10xz;B = 4'b0011;C = 4'bz011;
A | B = 4'b10xz | 4'b0011 = 4'b1011;
A | C = 4'b10xz | 4'bz011 = 4'b1011;
单目操作
一个4bit的数对自己进行按位或,输出的结果为1bit的数。
假设A = 4'b10xz;B = 4'b0011;
| A = A[3] || A[2] || A[1] || A[0] = 1
| B = 1
因为4bit数A和B中间都有1,所以A、B按位或结果都为1。
若C = 4'b00xz;则 | C = x
相等运算符(==)
参与比较的两个操作数必须逐位相等,其相等比较的结果才为 1, 如果某些位是不定态或高阻值,其相等比较得到的结果是不定值。
相等运算符的比较,只要等式的两端有x或者高阻态z出现,那么结果就是一定是x,譬如:
(4'b1010 == 4'b101x)= x
(4'b101z == 4'b1010)= x
(4'b10x1 == 4'b10x1)= x
(4'b1011 == 4'b1011)= 1
(4'b1010 == 4'b1011)= 0
全等运算符(===)
全等比较是对这些不定态或高阻值的位也进行比较,两个操作数必须完全一致,其结果才是 1,否则结果是 0。
(4'b1010 === 4'b101x)= 0
(4'b101z === 4'b1010)= 0
(4'b101z === 4'b101z)= 1
(4'b101x === 4'b101x)= 1
相等运算符和全等运算符的真值表
== | 0 | 1 | x | z | === | 0 | 1 | x | z |
0 | 1 | 0 | x | x | 0 | 1 | 0 | 0 | 0 |
1 | 0 | 1 | x | x | 1 | 0 | 1 | 0 | 0 |
x | x | x | x | x | x | 0 | 0 | 1 | 0 |
z | x | x | x | x | z | 0 | 0 | 0 | 1 |
相关文章:
、按位与()、逻辑或(||)、按位或(|)、等于(==)、全等(===)的区别)
Verilog 逻辑与()、按位与()、逻辑或(||)、按位或(|)、等于(==)、全等(===)的区别
逻辑与(&&)逻辑与是一个双目运算符,当符号两边为1时输出1,符号两边为0时输出0。真值表:&&01xz00000101xxx0xxxz0xxx两个4bit的数字相与;A4b0x1z;B4b01xx;C4b00xz&am…...

剑指 Offer 22. 链表中倒数第k个节点
剑指 Offer 22. 链表中倒数第k个节点 难度:easy\color{Green}{easy}easy 题目描述 输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。 例如,一个链…...

数据结构预算法之买卖股票的最好时机(三)动态规划
目录:一.题目知识点:动态规划二.动态规划数组思路确定1.dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组一.题目知识点:动态规划动态规划算法的基本思想是:将待求解的问题分解成若干个相互联…...
【数通网络交换基础梳理2】三层设备、网关、ARP表、VLAN、路由表及跨网段路由下一跳转发原理
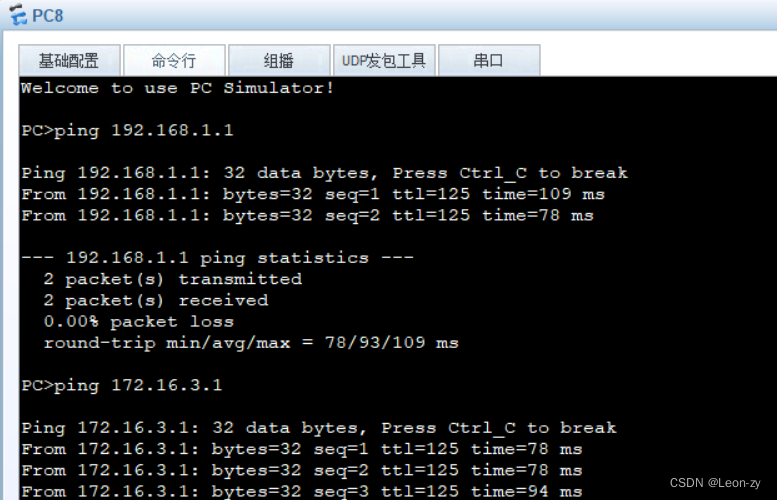
一、不同网段如何通讯 同网段可以依靠二层交换机通讯,网络中存在多个网段192.168.1.1/24 172.16.1.1/24 173.73.1.1/24情况下如何互相通讯?上节留一下的问题,这节继续讲解。 1、这里以Ping命令讲解,PC1 ping173.73.1.2…...
Java-排序链表问题
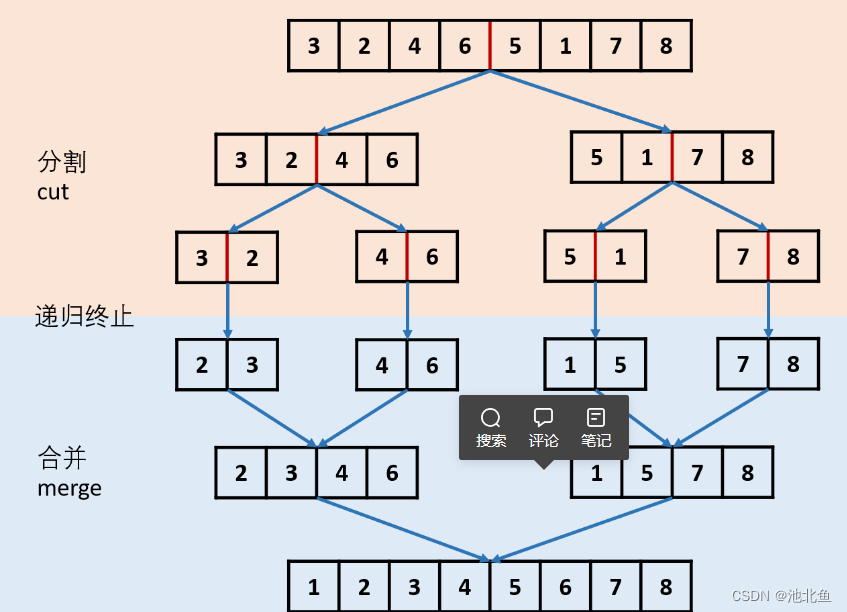
Java-排序链表问题题目题解方法:自顶向下归并排序算法题目 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 示例 1: 示例 2: 示例 3: 提示: *链表中节点的数目在范围 [0, 5 * 104]…...
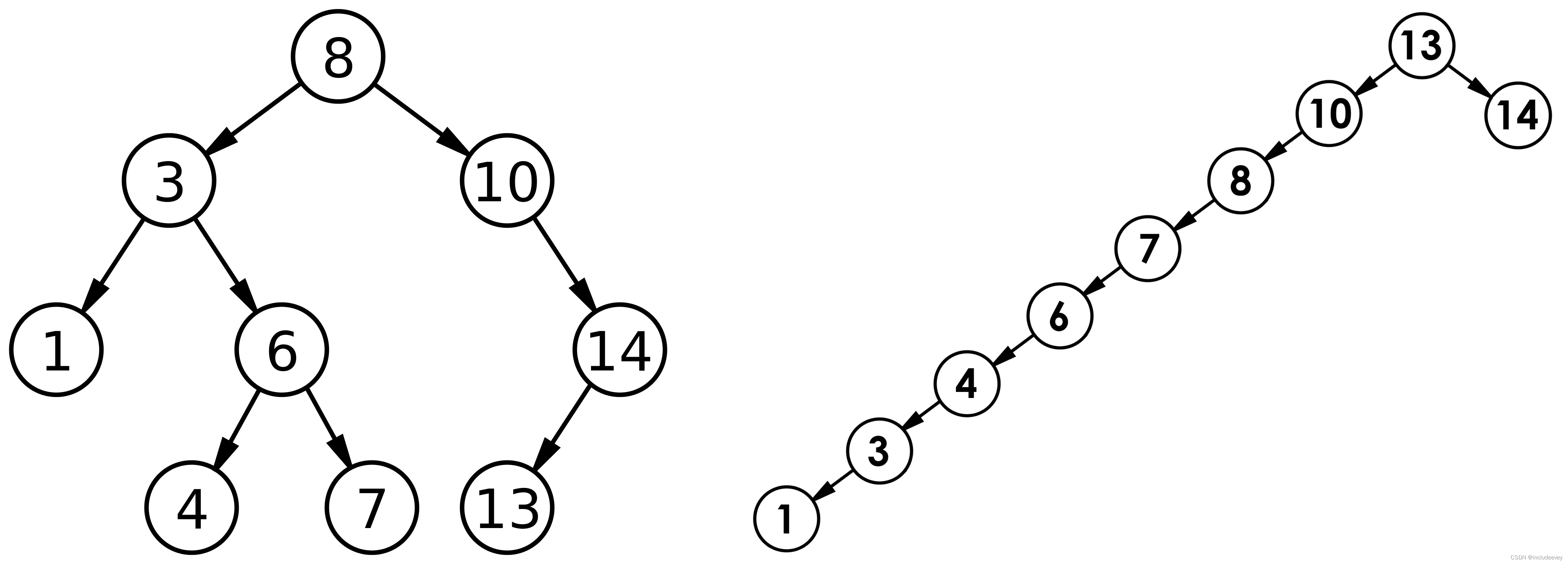
c++之二叉树【进阶版】
前言 在c语言阶段的数据结构系列中已经学习过二叉树,但是这篇文章是二叉树的进阶版,因为首先就会讲到一种树形结构“二叉搜索树”,学习二叉搜索树的目标是为了更好的理解map和set的特性。二叉搜索树的特性就是左子树键值小于根,右…...
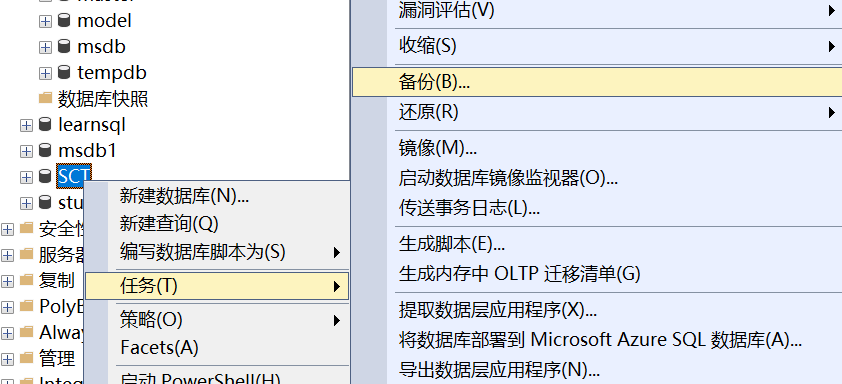
【数据库】 SQLServer
SQL Server 安装 配置 修改SQL Server默认的数据库文件保存路径_ 认识 master :是SQL Server中最重要的系统数据 库,存储SQL Server中的元数据。 Model:模板数据库,在创建新的数据库时,SQL Server 将会复制此数据…...

Linux 4.19 内核中 spinlock 概览
Linux内核中 spinlock相关数据结构和代码实现涉及的文件还是挺多的,这篇博客尝试从文件的角度来梳理一下 spinlock的相关数据结构和代码实现,适合想大概了解 Linux内核中 spinlock从上层 API到底层实现间的调用路径和传参变化,尤其适合了解 s…...
:基本概念TensorFlow的基本介绍,图,会话,会话中的run(),placeholder(),常见的报错)
TensorFlow 1.x学习(系列二 :1):基本概念TensorFlow的基本介绍,图,会话,会话中的run(),placeholder(),常见的报错
目录1.基本介绍2.图的结构3.会话,会话的run方法4.placeholder5.返回值异常写在前边的话:之前发布过一个关于TensorFlow1.x的转载系列,自己将基本的TensorFlow操作敲了一遍,但是仍然有很多地方理解的不够深入。所以重开一个系列&am…...
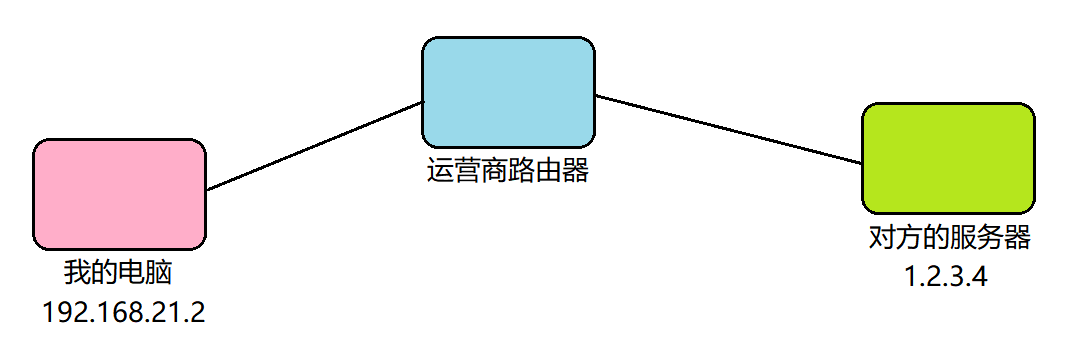
javaEE 初阶 — 关于 IPv4、IPv6 协议、NAT(网络地址转换)、动态分配 IP 地址 的介绍
文章目录1. IPv42. IPv63. NAT4. 动态分配 IP 地址1. IPv4 在互联网的世界中只有 0 和1 ,所以每个人都有一个由 0 和 1 组成的地址来让别人找到你。 这段由 0 和 1 组成的地址叫 IP 地址,这是互联网的基础资源,可以简单的理解为互联网的土地。…...
《Qt 6 C++开发指南》简介
我们编写的新书《Qt 6 C开发指南》在2月份终于正式发行销售了,这本书是对2018年5月出版的《Qt 5.9 C开发指南》的重磅升级。以下是本书前言的部分内容,算是对《Qt 6 C开发指南》的一个简介。1.编写本书的目的《Qt 5.9C开发指南》是我写的第一…...
CleanMyMac是什么清理软件?及使用教程
你知道CleanMyMac是什么吗?它的字面意思为“清理我的Mac”,作为软件,那就是一款Mac清理工具,Mac OS X 系统下知名系统清理软件,是数以万计的Mac用户的选择。它可以流畅地与系统性能相结合,只需简单的步骤就…...

Linux小黑板(9):共享内存
"My poor lost soul"上章花了不少的篇幅讲了讲基于管道((匿名、命名))技术实现的进程间通信。进程为什么需要通信?目的是为了完成进程间的"协同",提高处理数据的能力、优化业务逻辑的实现等等,在linux中我们已经谈过了一个通信的大类…...
Detr源码解读(mmdetection)
Detr源码解读(mmdetection) 1、原理简要介绍 整体流程: 在给定一张输入图像后,1)特征向量提取: 首先经过ResNet提取图像的最后一层特征图F。注意此处仅仅用了一层特征图,是因为后续计算复杂度原因,另外&am…...
一个.Net Core开发的,撑起月6亿PV开源监控解决方案
更多开源项目请查看:一个专注推荐.Net开源项目的榜单 项目发布后,对于我们程序员来说,项目还不是真正的结束,保证项目的稳定运行也是非常重要的,而对于服务器的监控,就是保证稳定运行的手段之一。对数据库、…...
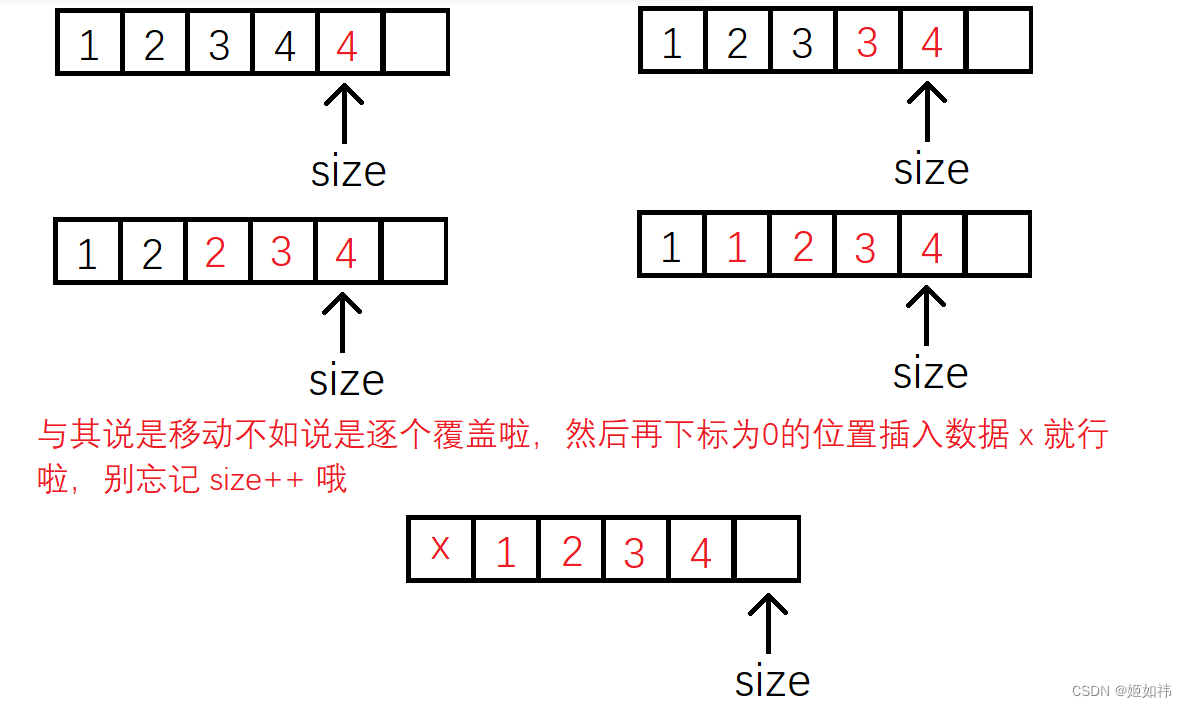
C语言数据结构初阶(2)----顺序表
目录 1. 顺序表的概念及结构 2. 动态顺序表的接口实现 2.1 SLInit(SL* ps) 的实现 2.2 SLDestory(SL* ps) 的实现 2.3 SLPrint(SL* ps) 的实现 2.4 SLCheckCapacity(SL* ps) 的实现 2.5 SLPushBack(SL* ps, SLDataType x) 的实现 2.6 SLPopBack(SL* ps) 的实现 2.7 SLP…...
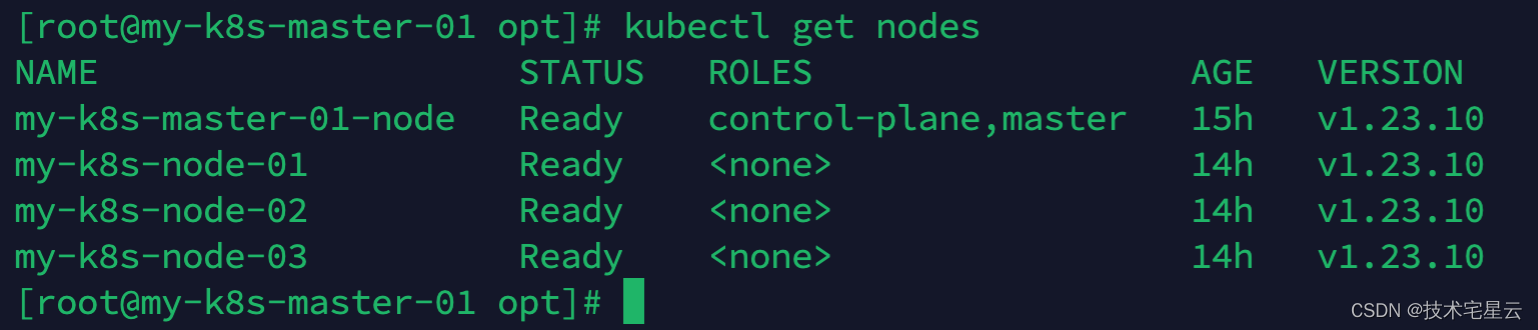
K8S常用命令速查手册
K8S常用命令速查手册一. K8S日常维护常用命令1.1 查看kubectl版本1.2 启动kubelet1.3 master节点执行查看所有的work-node节点列表1.4 查看所有的pod1.5 检查kubelet运行状态排查问题1.6 诊断某pod故障1.7 诊断kubelet故障方式一1.8 诊断kubelet故障方式二二. 端口策略相关2.1 …...

Linux系统下命令行安装MySQL5.6+详细步骤
1、因为想在腾讯云的服务器上创建自己的数据库,所以我在这里是通过使用Xshell 7来连接腾讯云的远程服务器; 2、Xshell 7与服务器连接好之后,就可以开始进行数据库的安装了(如果服务器曾经安装过数据库,得将之前安装的…...
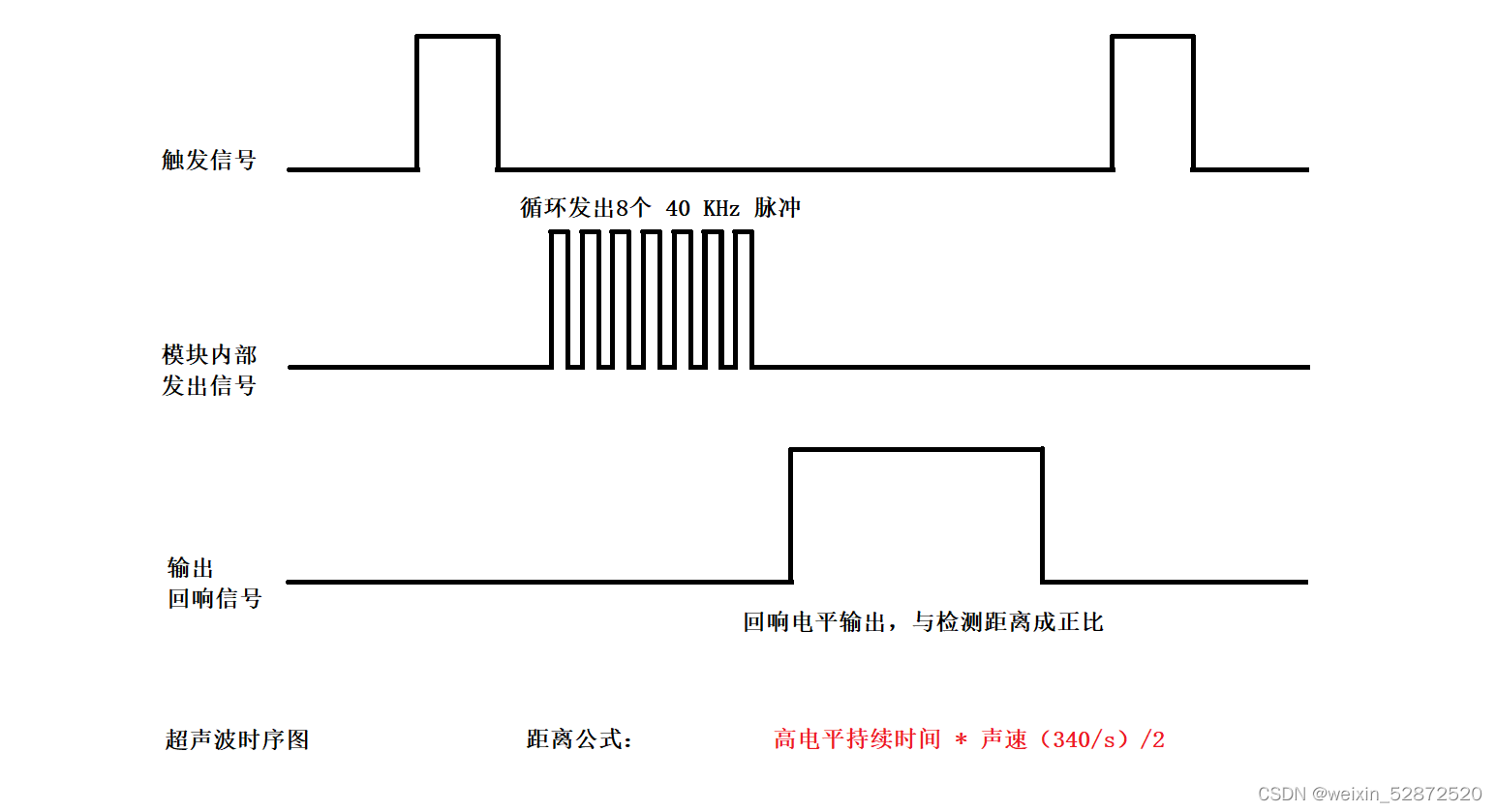
13.STM32超声波模块讲解与实战
目录 1.超声波模块讲解 2.超声波时序图 3.超声波测距步骤 4.项目实战 1.超声波模块讲解 超声波传感器模块上面通常有两个超声波元器件,一个用于发射,一个用于接收。电路板上有4个引脚:VCC GND Trig(触发)ÿ…...

逆向之Windows PE结构
写在前面 对于Windows PE文件结构,个人认为还是非常有必要掌握和了解的,不管是在做逆向分析、免杀、病毒分析,脱壳加壳都是有着非常重要的技能。但是PE文件的学习又是一个非常枯燥过程,希望本文可以帮你有一个了解。 PE文件结构…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
