动态规划-规划兼职工作
动态规划-规划兼职工作
一、问题描述
你打算利用空闲时间来做兼职工作赚些零花钱。这里有 n 份兼职工作,每份工作预计从 startTime 开始到 endTime 结束,报酬为 profit。给你一份兼职工作表,包含开始时间 startTime,结束时间 endTime 和预计报酬 profit 三个数组,请你计算并返回可以获得的最大报酬。
注意:
-
时间上出现重叠的 2 份工作不能同时进行。
-
如果你选择的工作在时间 X 结束,那么你可以立刻进行在时间 X 开始的下一份工作。
二、问题分析
例如现在输入一组数据:
-
startTime = [1,2,3,3]
-
endTime = [3,4,5,6]
-
profit = [50,10,40,70]
表示兼职表有4份工作:
工作1:开始时间:1,结束时间:3,薪资:50
工作2:开始时间:2,结束时间:4,薪资:10
工作3:开始时间:3,结束时间:5,薪资:40
工作4:开始时间:3,结束时间:6,薪资:70
第一步:找出最优解的性质,并刻画其结构特征。
简单尝试穷举法:
方案1:工作1或工作2=50或10
方案2:工作1+工作3=50+40=90
方案3:工作1+工作4=50+70=120
…
发现问题:组合很多,由于有起始时间和结束时间导致没有很好的排序组合方案

三、动态规划方程,即递归关系
第二步:递归定义最优值

- dp[i] 表示前i份兼职工作可以获得的最大报酬。
- k 表示满足结束时间小于等于第i−1 份工作开始时间的兼职工作数量。
- profit[i−1]表示第i份工作的薪酬。
- 该公式表示:完成第i份兼职获得的最大报酬=MAX(考虑前一份(i-1)兼职的最大报酬,第i份兼职开始时间前能完成的兼职的最大报酬+第i份兼职的报酬)。
四、代码分析
第三步:自底向上的方式计算最值
1.基本代码和解释
public static int jobScheduling(int[] startTime, int[] endTime, int[] profit, int[] dp, String[] optimal) {// 工作数量int n = startTime.length;// 存储工作的int[][] jobs = new int[n][];// 放入for (int i = 0; i < n; i++) {jobs[i] = new int[]{startTime[i], endTime[i], profit[i]};}// 按结束时间排序Arrays.sort(jobs, Comparator.comparingInt(a -> a[1]));// 对每份工作判断for (int i = 1; i <= n; i++) {// 查找合适的工作// k 表示满足结束时间小于等于第i−1份工作开始时间的兼职工作数量int k = binarySearch(jobs, i - 1, jobs[i - 1][0]);// dp[i]=max(dp[i−1],dp[k]+profit[i−1])// 每份工作薪资和(前一份工作薪资,当前工作开始时间前可以结束的工作薪资+当前工作薪资)dp[i] = Math.max(dp[i - 1], dp[k] + jobs[i - 1][2]);//判断是否选择了i兼职if (dp[i] == dp[i - 1]) {// 如果未选择,表示i-1前是最优解optimal[i] = optimal[i - 1];} else {// 如果选择表示:最优解=i开开始前最优解+ioptimal[i] = (optimal[k] + " " + String.valueOf(i)).trim();}}return dp[n];
}
public static int binarySearch(int[][] jobs, int right, int target) {int left = 0;while (left < right) {int mid = left + (right - left) / 2;if (jobs[mid][1] > target) {right = mid;} else {left = mid + 1;}}return left;}
2.测试
public static void main(String[] args) {// 开始时间int[] startTime = {1, 2, 3, 3};// 结束时间int[] endTime = {3, 4, 5, 6};// 薪资表int[] profit = {50, 10, 40, 70};// 报酬数组int[] dp = new int[startTime.length + 1];// 最优解数组String[] optimal = new String[startTime.length + 1];optimal[0] = " ";int i = jobScheduling(startTime, endTime, profit, dp, optimal);System.out.println("共获得报酬=" + i);System.out.println("工作和薪酬关系=" + Arrays.toString(dp));System.out.println("最优兼职表=" + Arrays.toString(optimal));
}
共获得报酬=120
工作和薪酬关系=[0, 50, 50, 90, 120]
最优兼职表=[ , 1, 1, 1 3, 1 4]
问题总结
在这道动态规划案例中:
-
要点
完成第i份兼职获得的最大报酬=MAX(考虑前一份(i-1)兼职的最大报酬,第i份兼职开始时间前能完成的兼职的最大报酬+第i份兼职的报酬)。
在计算时考虑当前兼职时,要用到之前子问题的解时,我们直接查兼职与最大薪资表dp就可以简化运算。 -
算法性能分析
- 时间复杂度:O(nlogn),其中 n 是兼职工作的数量。排序需要 O(nlogn),遍历 + 二分查找需要 O(nlogn),因此总时间复杂度为 O(nlogn)。
- **空间复杂度:O(n)。**需要 O(n) 的空间来保存dp。
-
现实意义
通过学习动态规划,弄懂该案例,不光可以学习如何兼职获取最大收益,也能用在其他和时间有关的规划问题中,
设计动态规划算法的步骤
(1)找出最优解的性质,并刻画其结构特性。
(2)递归地定义最优值。
(3)以自底向上的方式计算最优值
(4)根据计算最优值时得到的信息,构建最优解。
相关文章:

动态规划-规划兼职工作
动态规划-规划兼职工作 一、问题描述 你打算利用空闲时间来做兼职工作赚些零花钱。这里有 n 份兼职工作,每份工作预计从 startTime 开始到 endTime 结束,报酬为 profit。给你一份兼职工作表,包含开始时间 startTime,结束时间 en…...

Redis学习笔记(二)Redis基础(基于5.0.5版本)
一、Redis定位与特性 Redis是一个速度非常快的非关系数据库(non-relational database),用 Key-Value 的形式来存储数据。数据主要存储在内存中,所以Redis的速度非常快,另外Redis也可以将内存中的数据持久化到硬盘上。…...

Ancaonda常用cmd命令总结
1) 查看以创建的虚拟环境: conda info --envs / conda env list 2) 激活创建的环境:conda activate xxx(虚拟环境名称) 3) 退出激活的环境:conda deactivate 4) 删除一个已有虚拟环境:conda remove --name(已创建虚拟…...

yolov5_reid【附代码,行人重识别,可做跨视频人员检测】
该项目利用yolov5reid实现的行人重识别功能,可做跨视频人员检测。 应用场景: 可根据行人的穿着、体貌等特征在视频中进行检索,可以把这个人在各个不同摄像头出现时检测出来。可应用于犯罪嫌疑人检索、寻找走失儿童等。 支持功能:…...
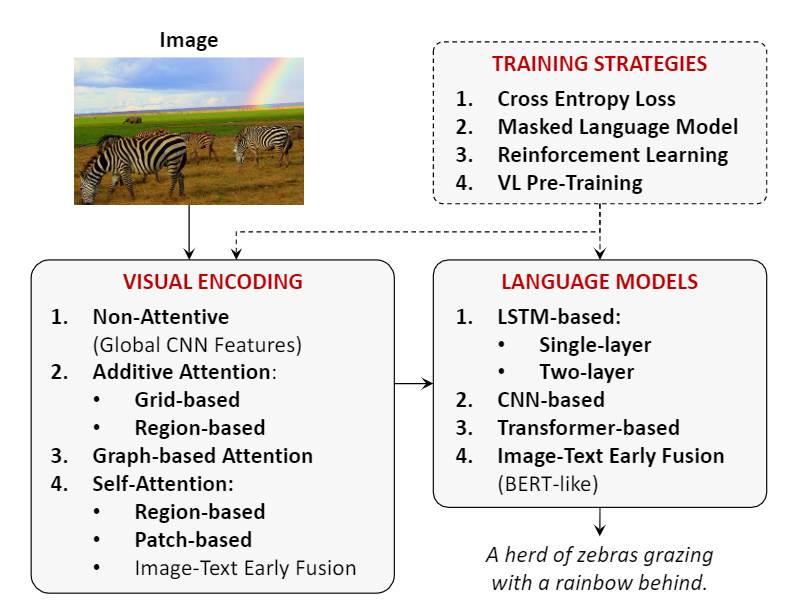
多模态预训练模型综述
经典预训练模型还未完成后续补上预训练模型在NLP和CV上取得巨大成功,学术届借鉴预训练模型>下游任务finetune>prompt训练>人机指令alignment这套模式,利用多模态数据集训练一个大的多模态预训练模型(跨模态信息表示)来解…...

华为OD机试题,用 Java 解【玩牌高手】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...
数学建模 latex 图片以及表格排版整理(overleaf)
无论是什么比赛,图片和表格的格式都非常重要,这边的重要不只是指规范性,还有抓住评委眼球的能力。 那么怎样抓住评委的眼球? 最重要的一点就是善用图片和表格(当然撰写论文最重要的是逻辑,这个是需要长期…...
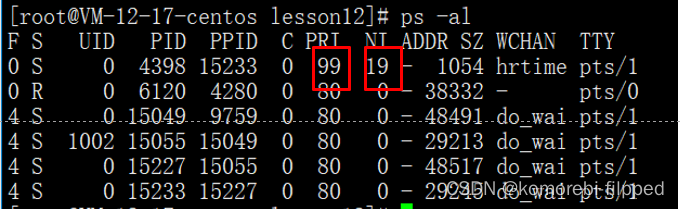
进程优先级(Linux)
目录 优先级VS权限 基本概念 查看系统进程 几个重要信息 PRI and NI PRI vs NI top命令 上限: 详细步骤 下限: 其他概念 优先级VS权限 权限:能or不能 优先级:已经能,但是谁先谁后的问题(CPU资源有…...
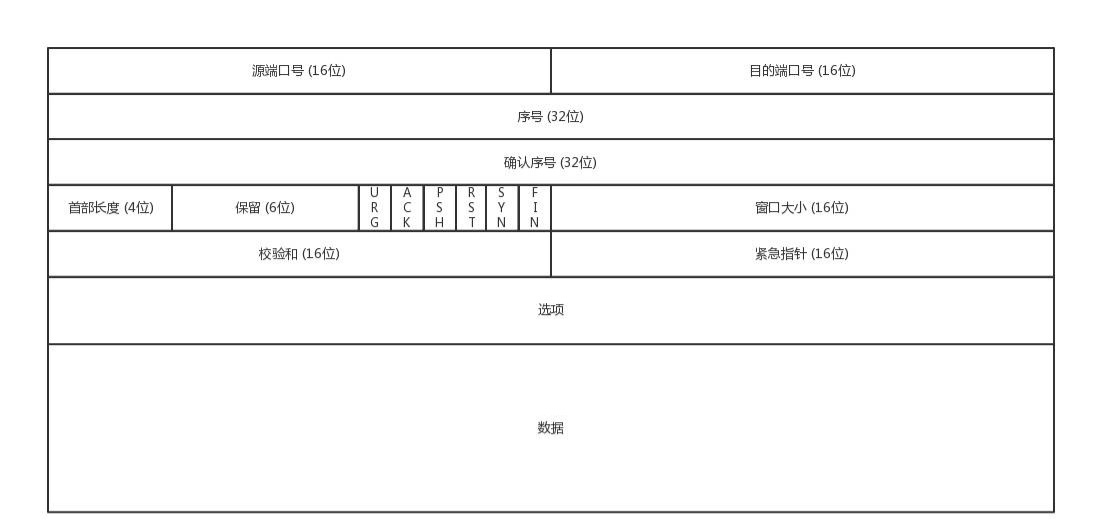
[面试直通版]网络协议面试核心之IP,TCP,UDP-TCP与UDP协议的区别
点击->计算机网络复习的文章集<-点击 目录 前言 UDP TCP 区别小总结 前言 TCP和UDP都是在传输层,在程序之间传输数据传输层OSI模型:第四层TCP/IP模型:第三层关键协议:TCP协议、UDP协议传输层属于主机间不同进程的通信传…...
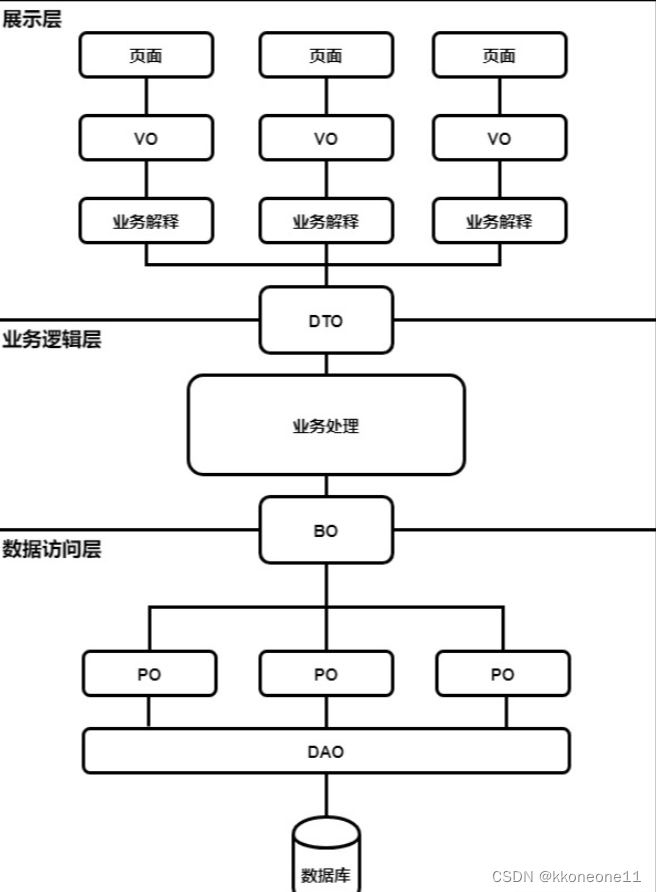
VO,BO,PO,DO,DTO,AO的区别
DTO(Data Transfer Object)数据传输对象 这个传输通常指的前后端之间的传输 1.在前端的时候: 存在形式通常是js里面的对象(也可以简单理解成json),也就是通过ajax请求的那个数据体 2.在后端的时候&…...

JavaSE学习笔记day15
零、 复习昨日 HashSet 不允许重复元素,无序 HashSet去重原理: 先比较hashcode,如果hashcode不一致,直接存储如果hashcode值一样,再比较equals如果equals值为true,则认为完全一样,不存储即去重否则存储 如果使用的是空参构造创建出的TreeSet集合,那么它底层使用的就是自然排序,…...
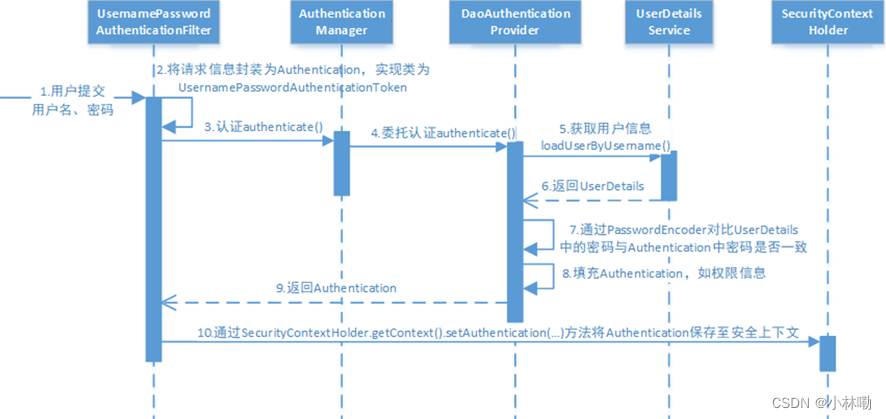
Spring Security认证研究
1.项目中认证的三种方式: 1.统一认证 认证通过由认证服务向给用户颁发令牌,相当于访问系统的通行证,用户拿着令牌去访问系统的资源。 2.单点登录,对于微服务项目,因为包含多个模块,所以单点登录就是使得用户…...

BigKey、布隆过滤器、分布式锁、红锁
文章目录 BigKey发现 BigKey如何删除BigKeyunlinkdelBigKey配置优化布隆过滤器布隆过滤器构建、使用、减少误判布隆过滤器二进制数组,如何处理删除?实现白名单 whitelistCustomer解决缓存穿透分布式锁依赖Redis 分布式锁代码使用红锁POM依赖yaml使用其他redis分布式锁容错率公…...
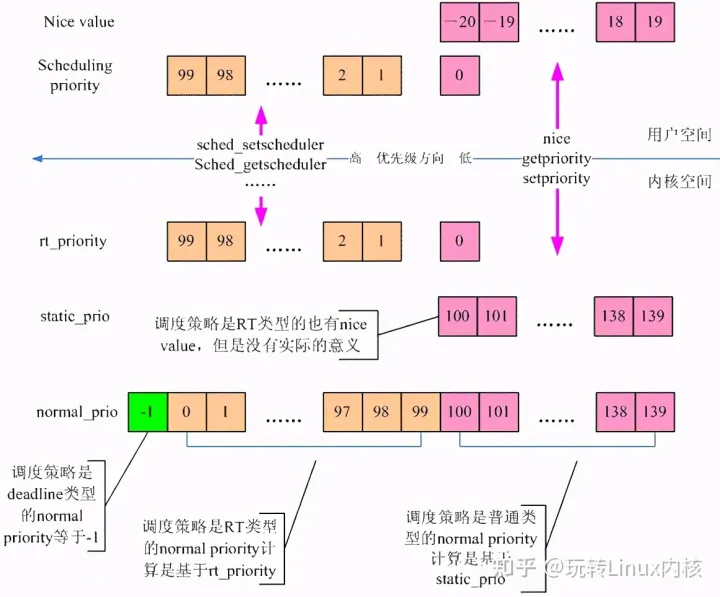
一文让你彻底理解Linux内核调度器进程优先级
一、前言 本文主要描述的是进程优先级这个概念。从用户空间来看,进程优先级就是nice value和scheduling priority,对应到内核,有静态优先级、realtime优先级、归一化优先级和动态优先级等概念。我们希望能在第二章将这些相关的概念描述清楚。…...

Java 抽象类和接口
文章目录一、抽象类1. 抽象类定义2. 抽象类成员特点二、接口1. 接口概述2. 接口成员特点3. 类和接口的关系4. 抽象类和接口的区别5. 接口案例三、形参和返回值一、抽象类 1. 抽象类定义 在 Java 中,一个没有方法体的方法应该定义为抽象方法,而类中如果…...
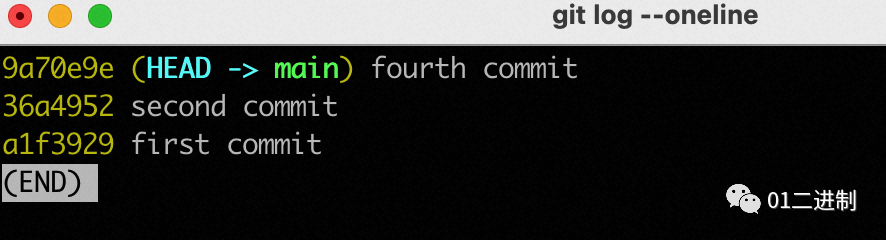
三行代码让你的git记录保持整洁
前言笔者最近在主导一个项目的架构迁移工作,由于迁移项目的历史包袱较重,人员合作较多,在迁移过程中免不了进行多分支、多次commit的情况,时间一长,git的提交记录便混乱不堪,随便截一个图形化的git提交历史…...

阿里巴巴内网 Java 面试 2000 题解析(2023 最新版)
前言 这份面试清单是今年 1 月份之后开始收集的,一方面是给公司招聘用,另一方面是想用它来挖掘在 Java 技术栈中,还有一些知识点是我还在探索的,我想找到这些技术盲点,然后修复它,以此来提高自己的技术水平…...
网络应用之静态Web服务器
静态Web服务器-返回固定页面数据学习目标能够写出组装固定页面数据的响应报文1. 开发自己的静态Web服务器实现步骤:编写一个TCP服务端程序获取浏览器发送的http请求报文数据读取固定页面数据,把页面数据组装成HTTP响应报文数据发送给浏览器。HTTP响应报文数据发送完…...

IndexDB 浏览器服务器
IndexDB 浏览器服务器 文章部分内容引用: https://www.ruanyifeng.com/blog/2018/07/indexeddb.html https://juejin.cn/post/7026900352968425486#heading-15 基本概念 数据库:IDBDatabase 对象对象仓库:IDBObjectStore 对象索引࿱…...
追梦之旅【数据结构篇】——详解C语言实现链队列
详解C语言实现链队列~😎前言🙌整体实现内容分析💞预备小知识🙌1.链队列头文件编写🙌2.链队列功能文件(Queue.c )编写:🙌1)初始化函数实现2)销毁函…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
