pytorch入门2--数据预处理、线性代数的矩阵实现、求导
数据预处理是指将原始数据读取进来使得能用机器学习的方法进行处理。
首先介绍csv文件:
CSV 代表逗号分隔值(comma-separated values),CSV 文件就是使用逗号分隔数据的文本文件。
一个 CSV 文件包含一行或多行数据,每一行数据代表一个记录。每个记录包含一个或多个数值,使用逗号进行分隔。另外,一个 CSV 文件中的所有数据行都包含相同数量的值。
我们通常使用 CSV 文件存储表格数据,很多软件都支持这种文件格式,例如 Microsoft Excel(新建工作簿保存为.csv即可) 和 Google Spreadsheet。
python可以使用内置的csv模块读取csv文件。
一、数据预处理
1.首先要找到jupyter notebook创建地文件存放地位置。
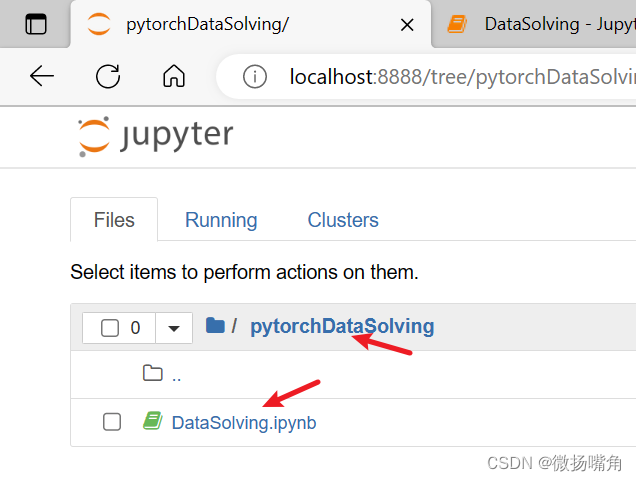
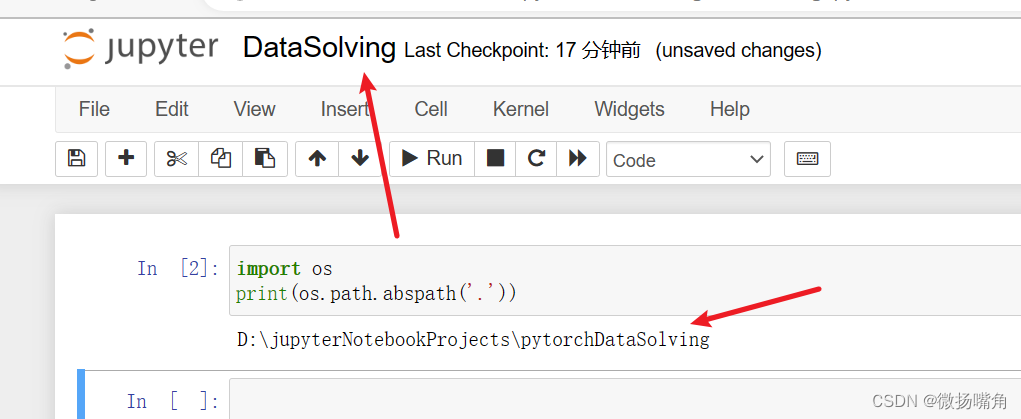
找到该路径。
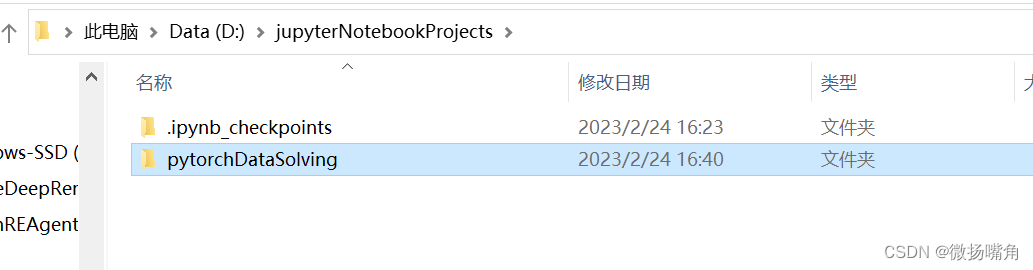
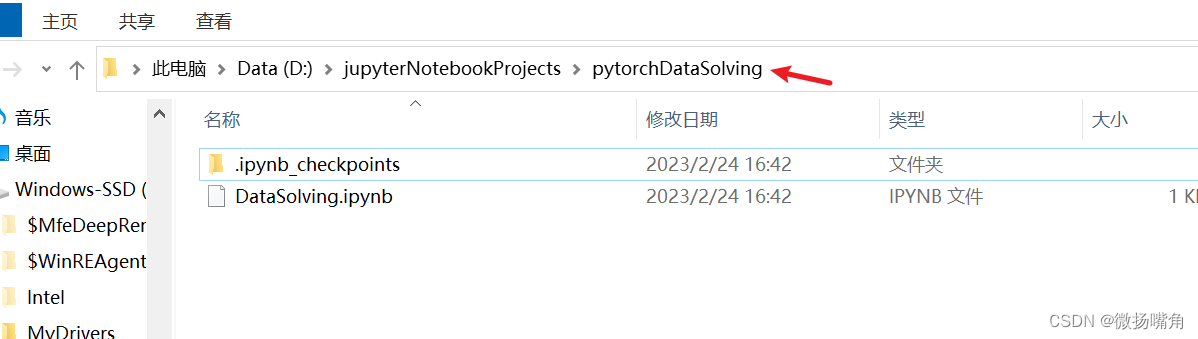
可以看出jupyter与保存地本地文件夹一致。
2.在jupyter notebook里的DataSolving中编写代码:
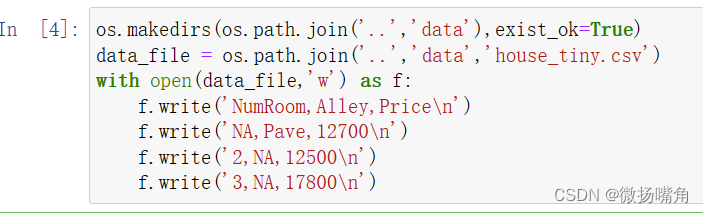
说明:(1)os.makedirs()用于递归地创建目录,exist_ok=True指定后如果该目录已存在也不报错;
(2)os.path.join()用于组合一个或多个路径名,os.path.join(‘…’,‘data’,‘house_tiny.csv’)的返回值为"…\data\house_tiny.cssv。
程序运行之后:
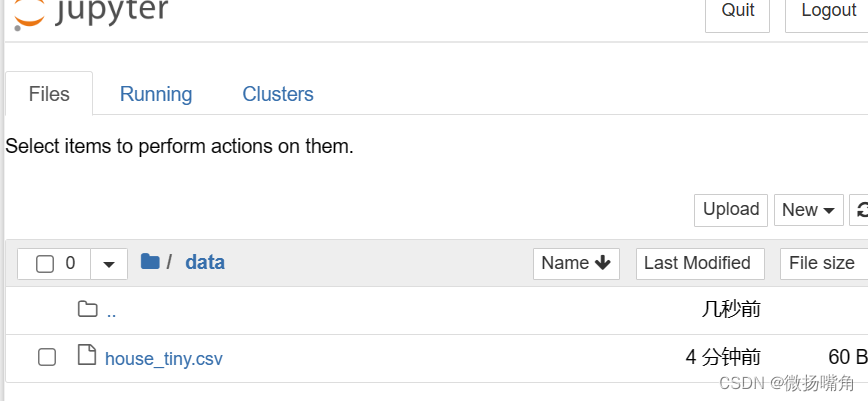
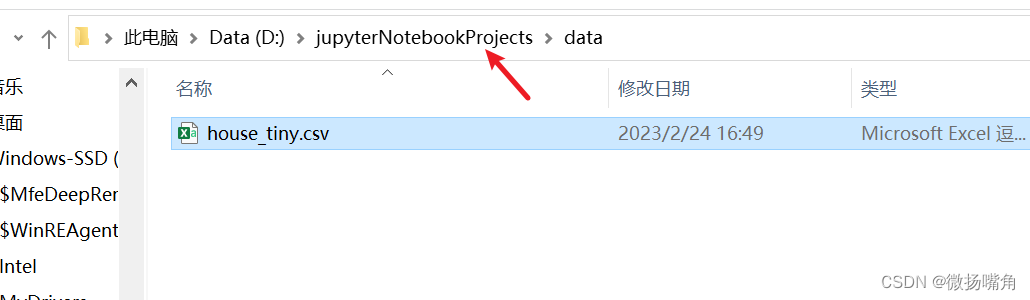
本地打开文件:
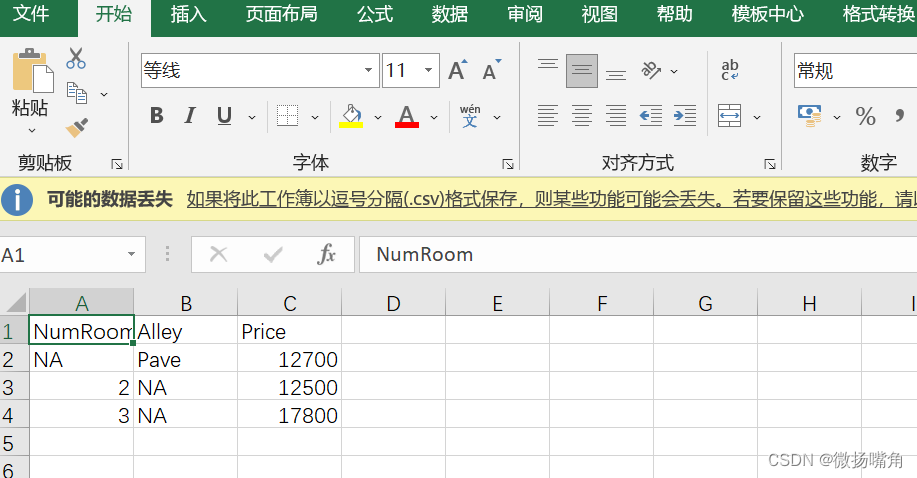
3.也可读取.csv文件,使用pandas。
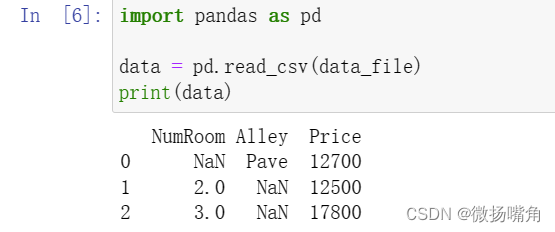
4.可以使用fillna()对.csv文件中的空值(不是0,而是缺失)进行填充。
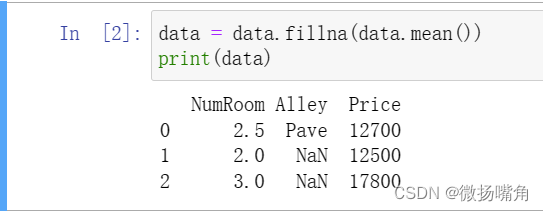
可以看到NumRoom那一列的空值被填上了均值(data.mean()表示一列的空值处填充该列原本不为空的元素的均值),而Alley那一列的空值没有被填充,因为该列是字符串,没有均值。
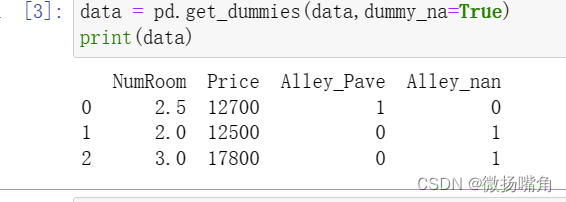
对于不是数值的,可以将空值是为一个类别,处理如下:
5.将从.csv文件中读取的数据转为torch张量。

二、矩阵
1.创建矩阵和矩阵的转置。

2.矩阵与向量的乘积torch.mv([矩阵名],[向量名])

3.矩阵与矩阵的运算torch.mm([矩阵名],[矩阵名])

4.矩阵的范数



5.矩阵计算(求导)
基于高数的知识,y=3x^2+2x,y’=6x+2,当x=2时,y’=14。该过程用pytorch实现为:

说明:(1)创建一个张量x,并设置其requires_grad参数为True,程序将会追踪所有对于该张量的操作,当完成计算后通过调用.backward(),自动计算所有的梯度(梯度相当于导数,即方向导数的最大值),这个张量所有的梯度将会自动累积到grad属性。这里x.grad是y关于x的导数。
(2)创建了一个关于x的函数y,torch.pow(x,2)相当于x2即x的平方。
(3)y.backward()是利用反向传播机制。

三种不同的求导情况:
(1)张量对标量求导:
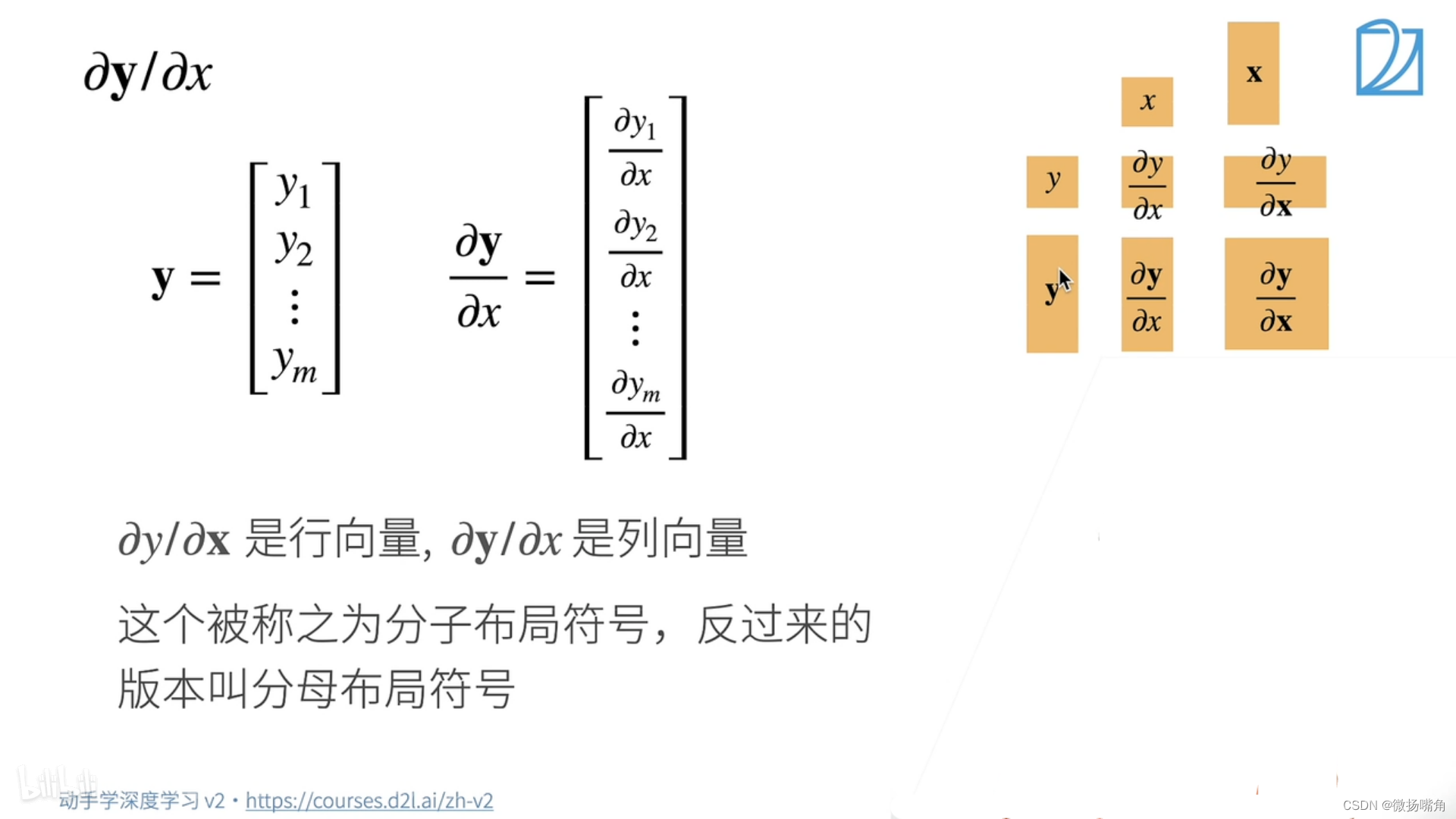
可以这样理解:
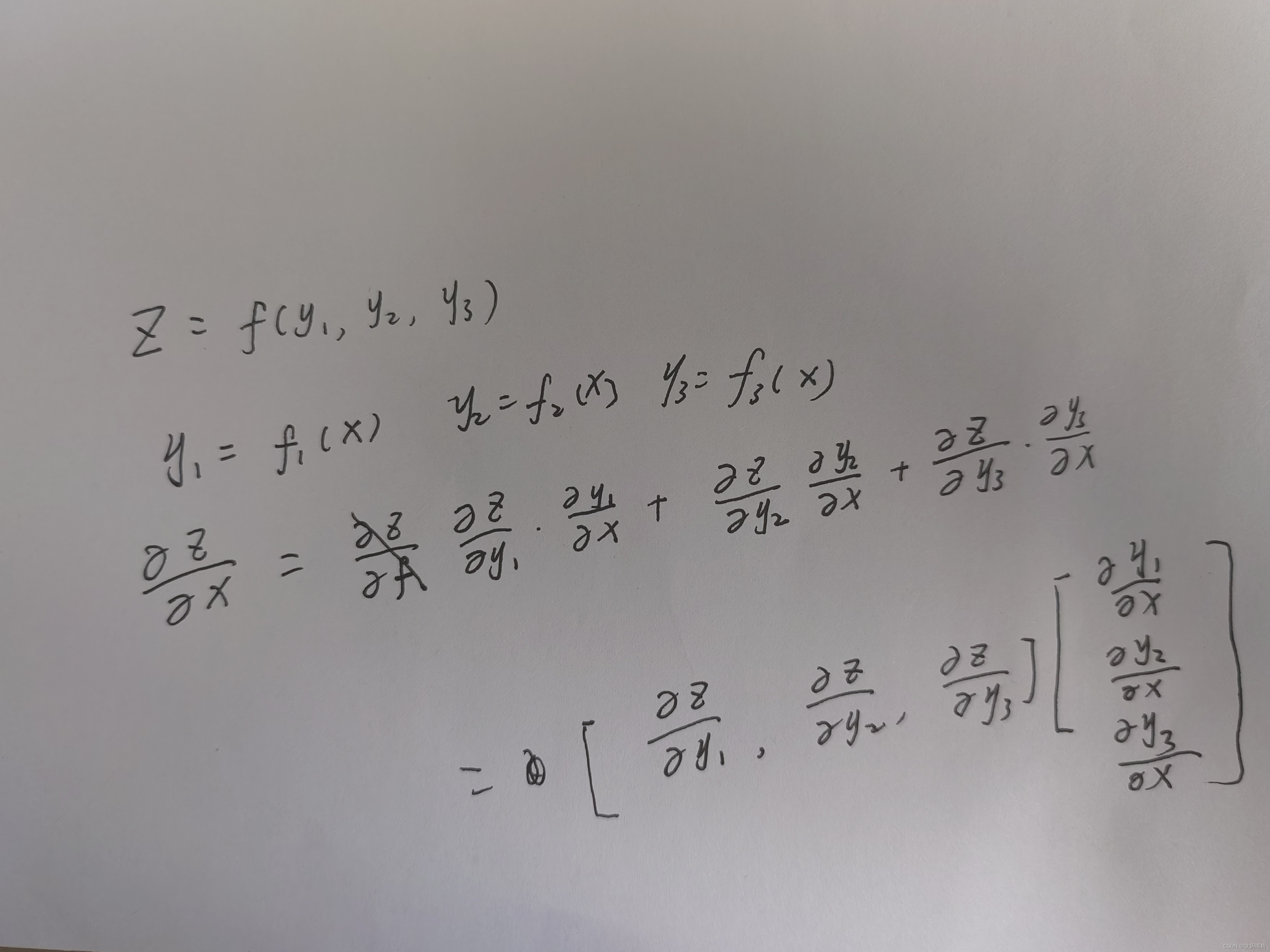
(2)标量对张量求导:
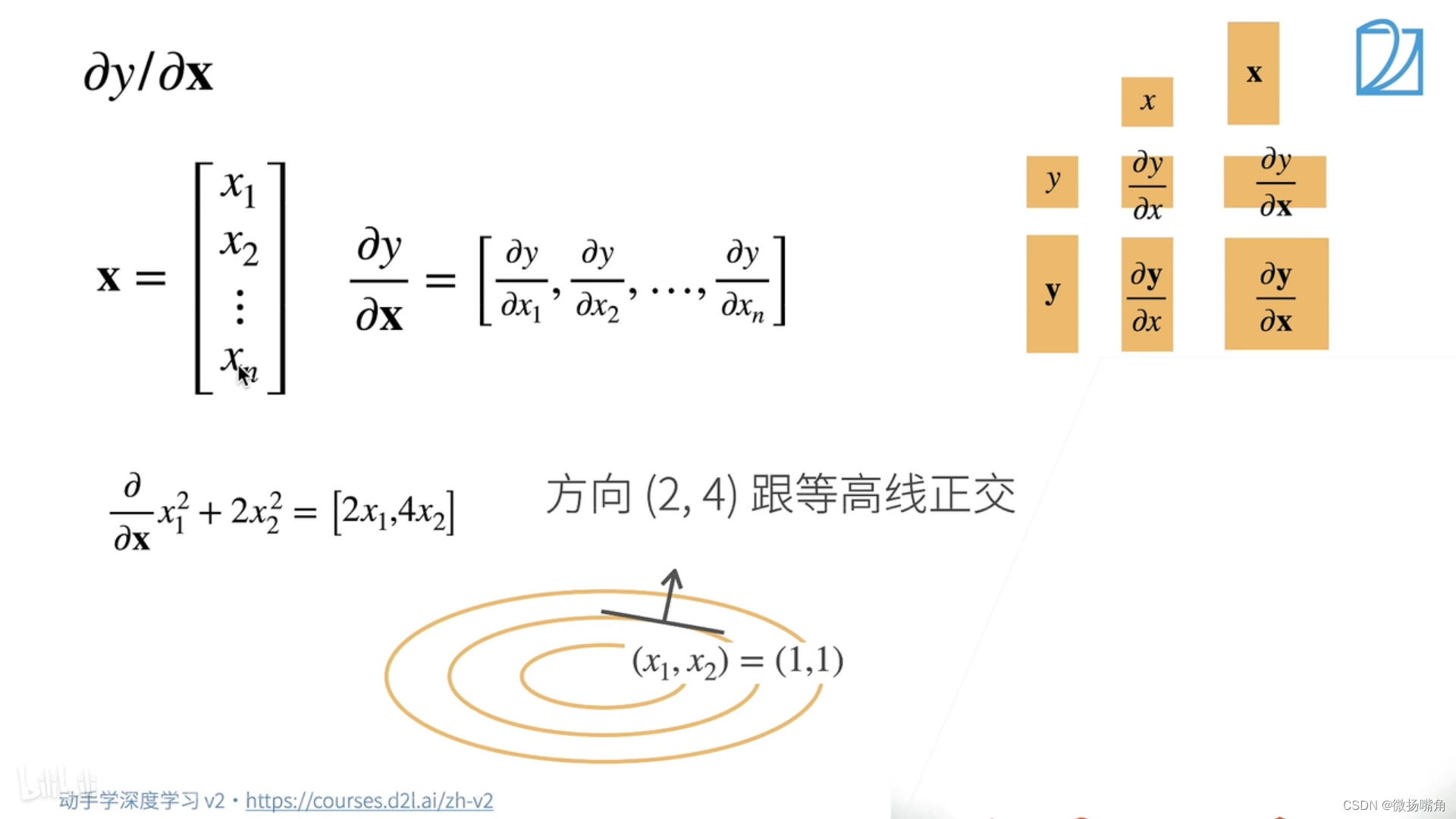
看下面的例子:

设x=[x1,x2,x3],则z=x12+x22+x32+6,则

标量对向量求导本质上是函数对各个自变量求导,这里只是把各个自变量看成一个向量。
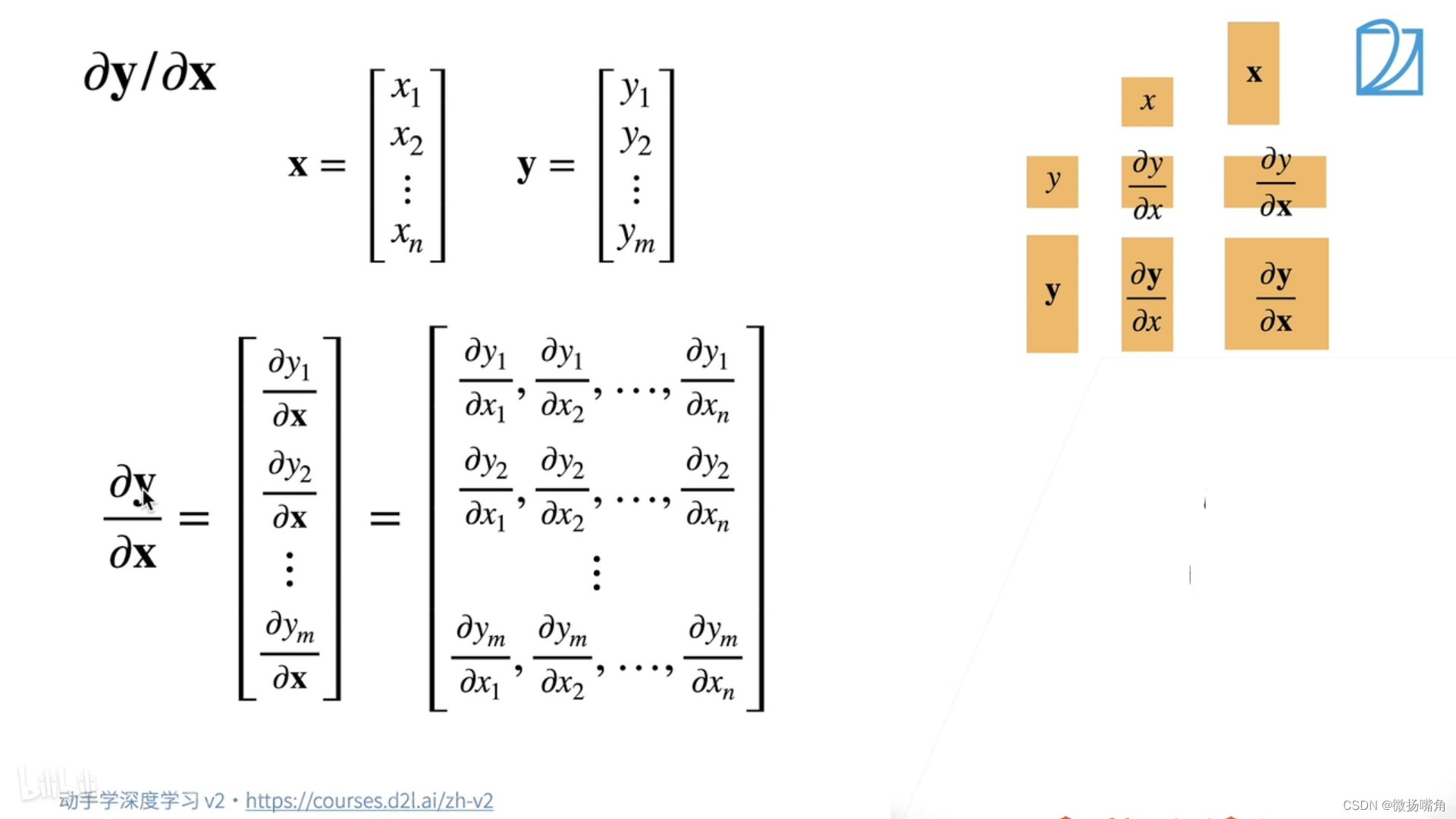
(3)张量对张量求导
理解:
现有如下问题,已知
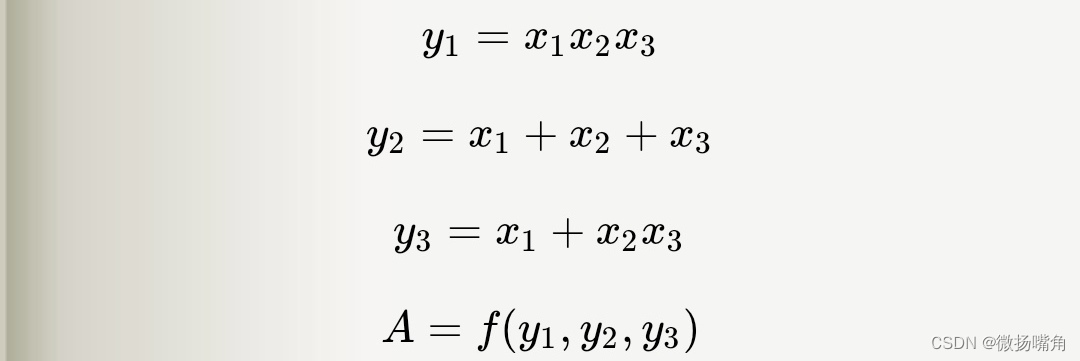
其中函数f(y1,y2,y3)的具体定义未知,现在求:
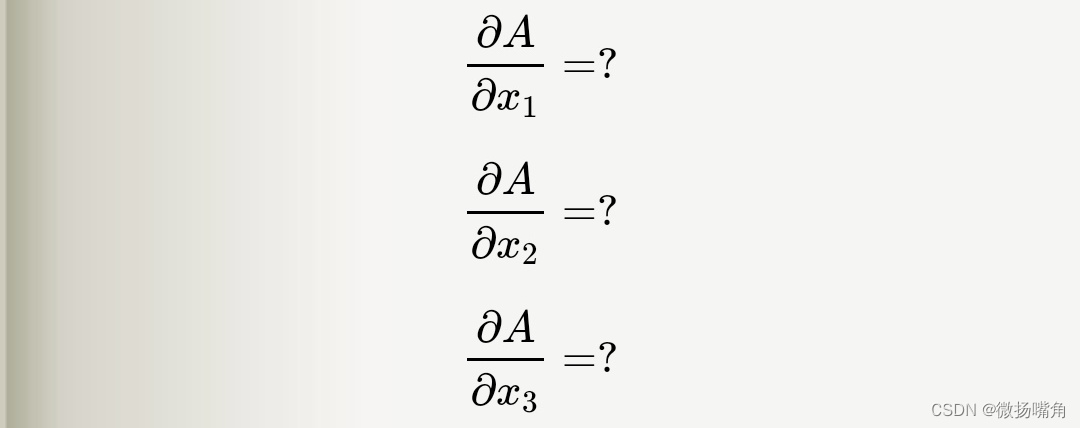
根据多元函数求导法则:

上面3个等式可以写成矩阵相乘的形式:

叫做雅可比式,雅可比式可以根据已知条件求出,哪怕不知道f(y1,y2,y3)的具体形式。
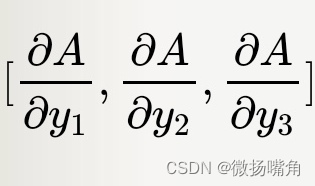
上面的张量是由pytorch的backward函数的gradient参数提供。
用pytorch实现:

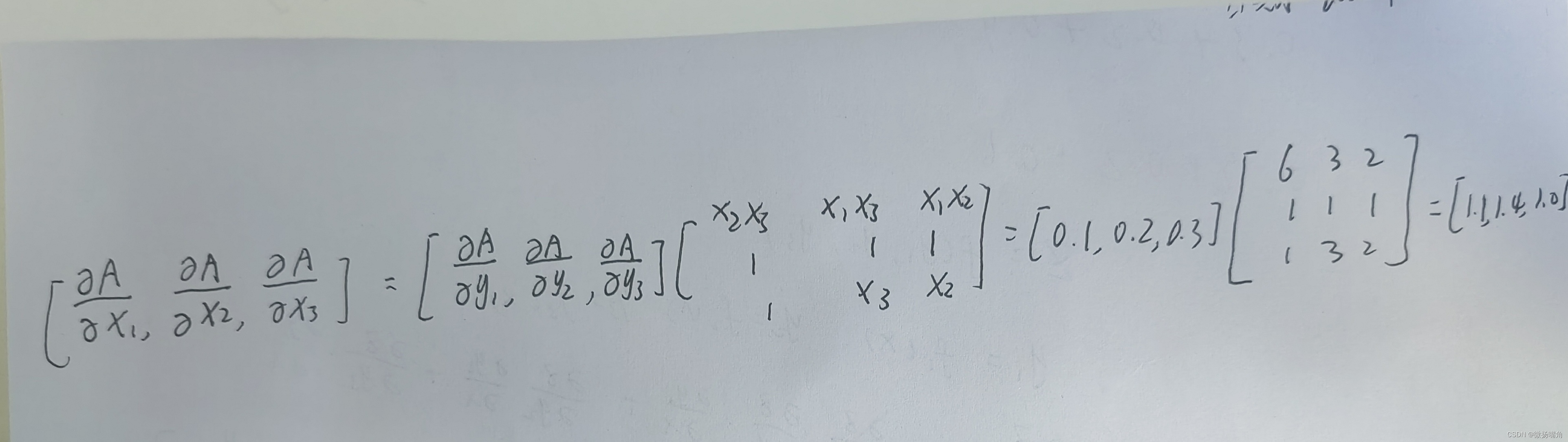
和代码运行结果一样。
补充:

相关文章:

pytorch入门2--数据预处理、线性代数的矩阵实现、求导
数据预处理是指将原始数据读取进来使得能用机器学习的方法进行处理。 首先介绍csv文件: CSV 代表逗号分隔值(comma-separated values),CSV 文件就是使用逗号分隔数据的文本文件。 一个 CSV 文件包含一行或多行数据,每一…...

15.消息队列RabbitMQ
一、基本概念 RabbitMQ 是一个开源的AMQP实现,服务器端用Erlang语言编写,支持多种客户端,如:Python、Ruby、.NET、Java、JMS、C、PHP、ActionScript、XMPP、STOMP等,支持AJAX。用于在分布式系统中存储转发消息…...

并发编程之死锁问题介绍
一、本文概览 死锁问题在并发编程中是一个非常致命的问题,问题一旦产生,只能通过重启机器、修改代码来修复问题,下面我们通过一小段文章内容介绍下死锁以及如何死锁的预防 二、什么是死锁? 在介绍死锁之前,先来明确下什…...
【python学习笔记】:SQL常用脚本(一)
1、行转列的用法PIVOT CREATE table test (id int,name nvarchar(20),quarter int,number int) insert into test values(1,N苹果,1,1000) insert into test values(1,N苹果,2,2000) insert into test values(1,N苹果,3,4000) insert into test values(1,N苹果,4,5000) insert…...
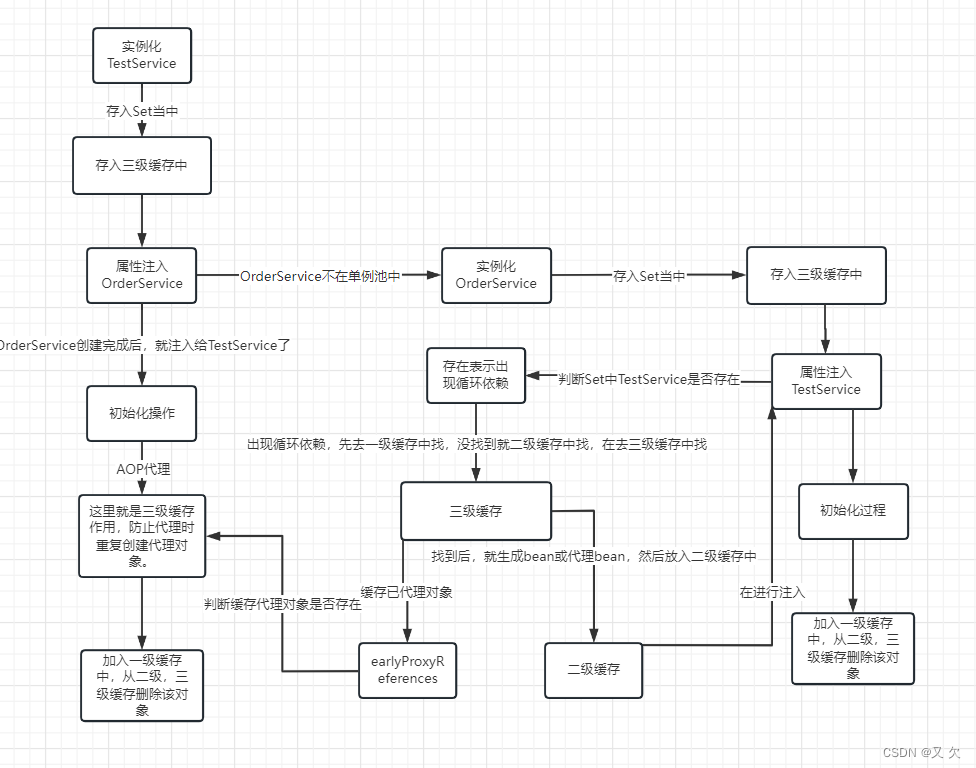
Spring是怎么解决循环依赖的
1.什么是循环依赖: 这里给大家举个简单的例子,相信看了上一篇文章大家都知道了解了spring的生命周期创建流程。那么在Spring在生命周期的哪一步会出现循环依赖呢? 第一阶段:实例化阶段 Instantiation 第二阶段:属性赋…...
HTML创意动画代码
目录1、动态气泡背景2、创意文字3、旋转立方体1、动态气泡背景 <!DOCTYPE html> <html> <head><title>Bubble Background</title><style>body {margin: 0;padding: 0;height: 100vh;background: #222;display: flex;flex-direction: colum…...

软工第一次个人作业——阅读和提问
软工第一次个人作业——阅读和提问 项目内容这个作业属于哪个课程2023北航敏捷软件工程这个作业的要求在哪里个人作业-阅读和提问我在这个课程的目标是体验敏捷开发过程,掌握一些开发技能,为进一步发展作铺垫这个作业在哪个具体方面帮助我实现目标对本课…...

urho3d的自定义文件格式
Urho3D尽可能使用现有文件格式,仅在绝对必要时才定义自定义文件格式。当前使用的自定义文件格式有: 二进制模型格式(.mdl) Model geometry and vertex morph data byte[4] Identifier "UMDL" or "UMD2" …...
spark第一章:环境安装
系列文章目录 spark第一章:环境安装 文章目录系列文章目录前言一、文件准备1.文件上传2.文件解压3.修改配置4.启动环境二、历史服务器1.修改配置2.启动历史服务器总结前言 spark在大数据环境的重要程度就不必细说了,直接开始吧。 一、文件准备 1.文件…...

MySQL---存储过程与存储函数的相关概念
MySQL—存储过程与存储函数的相关概念 存储函数和存储过程的主要区别: 存储函数一定会有返回值的存储过程不一定有返回值 存储过程和函数能后将复杂的SQL逻辑封装在一起,应用程序无需关注存储过程和函数内部复杂的SQL逻辑,而只需要简单地调…...

PMP值得考吗?
第一,PMP的价值体现 1、PMP是管理岗位必考证书。 多数企业会选择优先录用持PMP证书的管理人才,PMP成为管理岗位的必考证书。PMP在很多外企和国内中大型企业非常受重视,中石油、中海油、华为等等都会给内部员工做培训。 这些机构对项目管理…...
)
Quartus 报错汇总(持续更新...)
1、Error (10663): Verilog HDL Port Connection error at top_rom.v(70): output or inout port "stcp" must be connected to a structural net expression输出变量stcp在原设计文件中已经定义为reg型,在实例化时不能再定义为reg型,而应该是…...
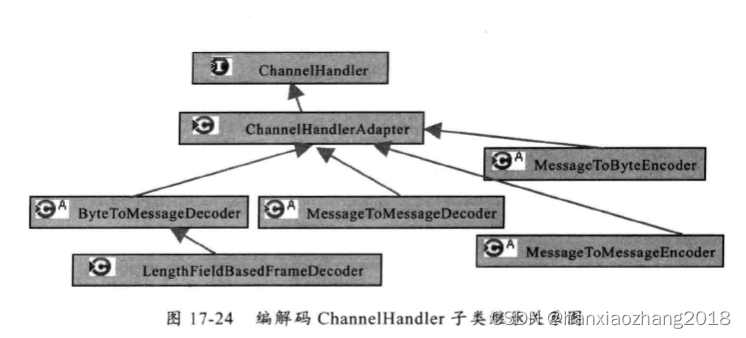
Netty权威指南总结(一)
一、为什么选择Netty:API使用简单,开发门槛低,屏蔽了NIO通信的底层细节。功能强大,预制了很多种编解码功能,支持主流协议。定制能力强,可以通过ChannelHandler对通信框架进行灵活地拓展。性能高、成熟、稳定…...

Elasticsearch:如何轻松安全地对实时 Elasticsearch 索引重新索引你的数据
在很多的时候,由于一些需求,我们不得不修改索引的映射,也即 mapping,这个时候我们需要重新索引(reindex)来把之前的数据索引到新的索引中。槽糕的是,我们的这个索引还在不断地收集实时数据&…...

【算法笔记】前缀和与差分
第一课前缀和与差分 算法是解决问题的方法与步骤。 在看一个算法是否优秀时,我们一般都要考虑一个算法的时间复杂度和空间复杂度。 现在随着空间越来越大,时间复杂度成为了一个算法的重要指标,那么如何估计一个算法的时间复杂度呢…...
)
python实战应用讲解-【实战应用篇】函数式编程-八皇后问题(附示例代码)
目录 知识储备-迭代器相关模块 itertools 模块 创建新的迭代器 根据最短输入序列长度停止的迭代器...
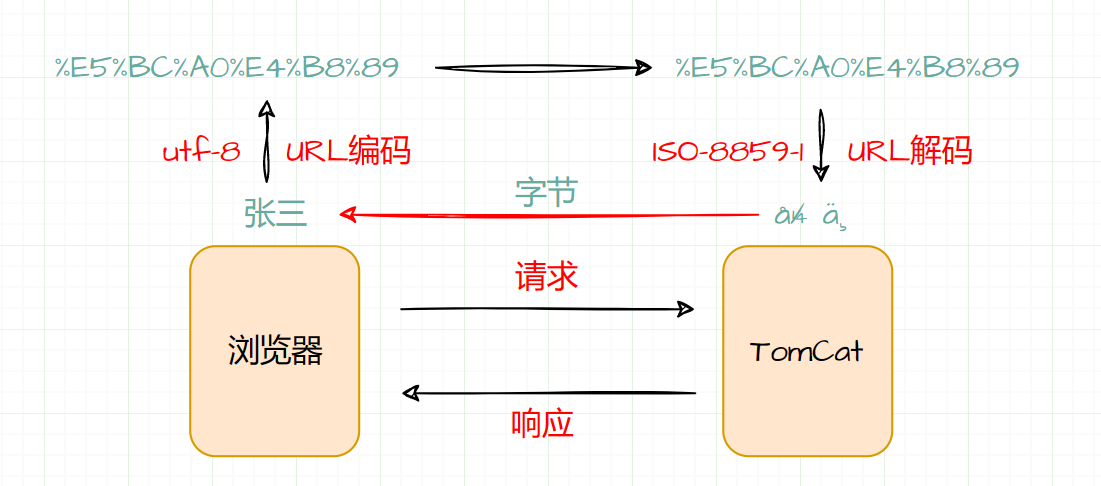
【Servlet篇】如何解决Request请求中文乱码的问题?
前言 前面一篇文章我们探讨了 Servlet 中的 Request 对象,Request 请求对象中封装了请求数据,使用相应的 API 就可以获取请求参数。 【Servlet篇】一文带你读懂 Request 对象 也许有小伙伴已经发现了前面的方式获取请求参数时,会出现中文乱…...

SpringBoot:SpringBoot简介与快速入门(1)
SpringBoot快速入门1. SpringBoot简介2. SpringBoot快速入门2.1 创建SpringBoot项目(必须联网,要不然创建失败,在模块3会讲到原因)2.2 编写对应的Controller类2.3 启动测试3. Spring官网构建工程4. SpringBoot工程快速启动4.1 为什…...
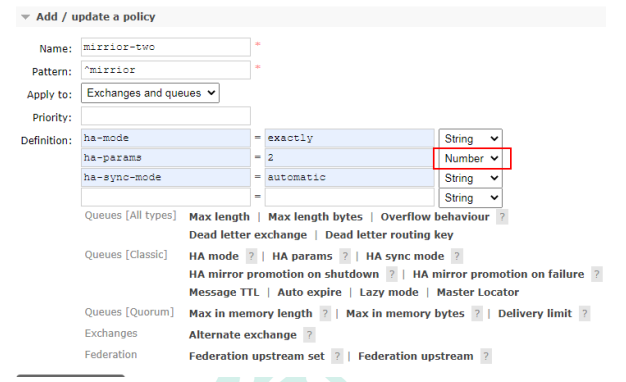
RabbitMQ学习(十一):RabbitMQ 集群
一、集群1.1 为什么要使用集群前面我们介绍了如何安装及运行 RabbitMQ 服务,不过这些是单机版的,无法满足目前真实应用的 要求。如果 RabbitMQ 服务器遇到内存崩溃、机器掉电或者主板故障等情况,该怎么办?单台 RabbitMQ 服务器可以…...
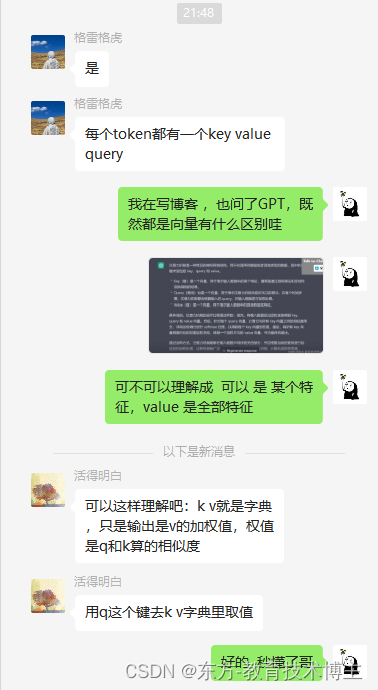
学渣适用版——Transformer理论和代码以及注意力机制attention的学习
参考一篇玩具级别不错的代码和案例 自注意力机制 注意力机制是为了transform打基础。 参考这个自注意力机制的讲解流程很详细, 但是学渣一般不知道 key,query,value是啥。 结合B站和GPT理解 注意力机制是一种常见的神经网络结构࿰…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
