自动驾驶之—2D到3D升维
前言:
最近在学习自动驾驶方向的东西,简单整理一些学习笔记,学习过程中发现宝藏up 手写AI
- 3D卷积
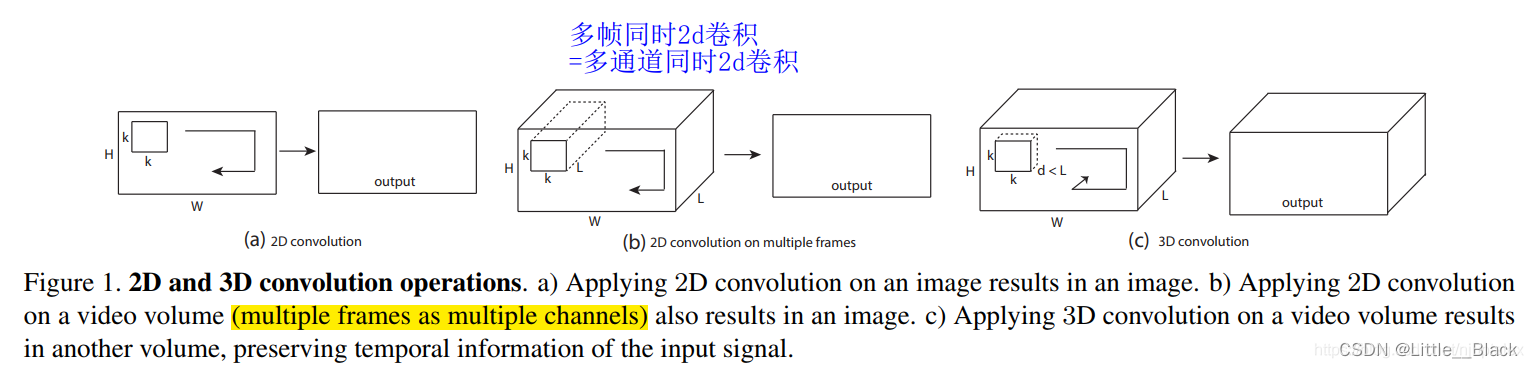
3D卷积的作用:对于2DCNN,我们知道可以很好的处理单张图片中的信息,但是其对于视频这种由多帧图像组成的图片流,以及CT****等一些医学上的3维图像就会显得束手无策。因为2D卷积没有考虑到图像之间时间维度上的物体运动信息的变化(3维CT图像也可以近似看为是二维图像在时间上的变化)。因此,为了能够对视频(包括3维医学图像)信息进行特征提取,以便用来分类及分割任务,提出了3D卷积,在卷积核中加入时间维度。
- pytorch中对应函数介绍
class torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
说明:
参数kernel_size,stride,padding,dilation可以是一个int的数据 - 卷积height和width值相同,也可以是一个有三个int数据的tuple数组,tuple的第一维度表示depth的数值,tuple的第二维度表示height的数值,tuple的第三维度表示width的数值
Parameters:
in_channels(int) – 输入的通道数
out_channels(int) – 输出的通道数
kernel_size(int or tuple) - 卷积核的尺寸
stride(int or tuple, optional) - 卷积步长
padding(int or tuple, optional) - 边缘填充的像素个数
dilation(int or tuple, optional) – 卷积核元素之间的间距
groups(int, optional) – 卷积的组数
bias(bool, optional) - 如果bias=True,添加偏置
举个栗子:
# With square kernels and equal stride
m = nn.Conv3d(16, 33, 3, stride=2)
# non-square kernels and unequal stride and with padding
m = nn.Conv3d(16, 33, (3, 5, 2), stride=(2, 1, 1), padding=(4, 2, 0))
input = autograd.Variable(torch.randn(20, 16, 10, 50, 100))
output = m(input)
- 3D卷积图示:
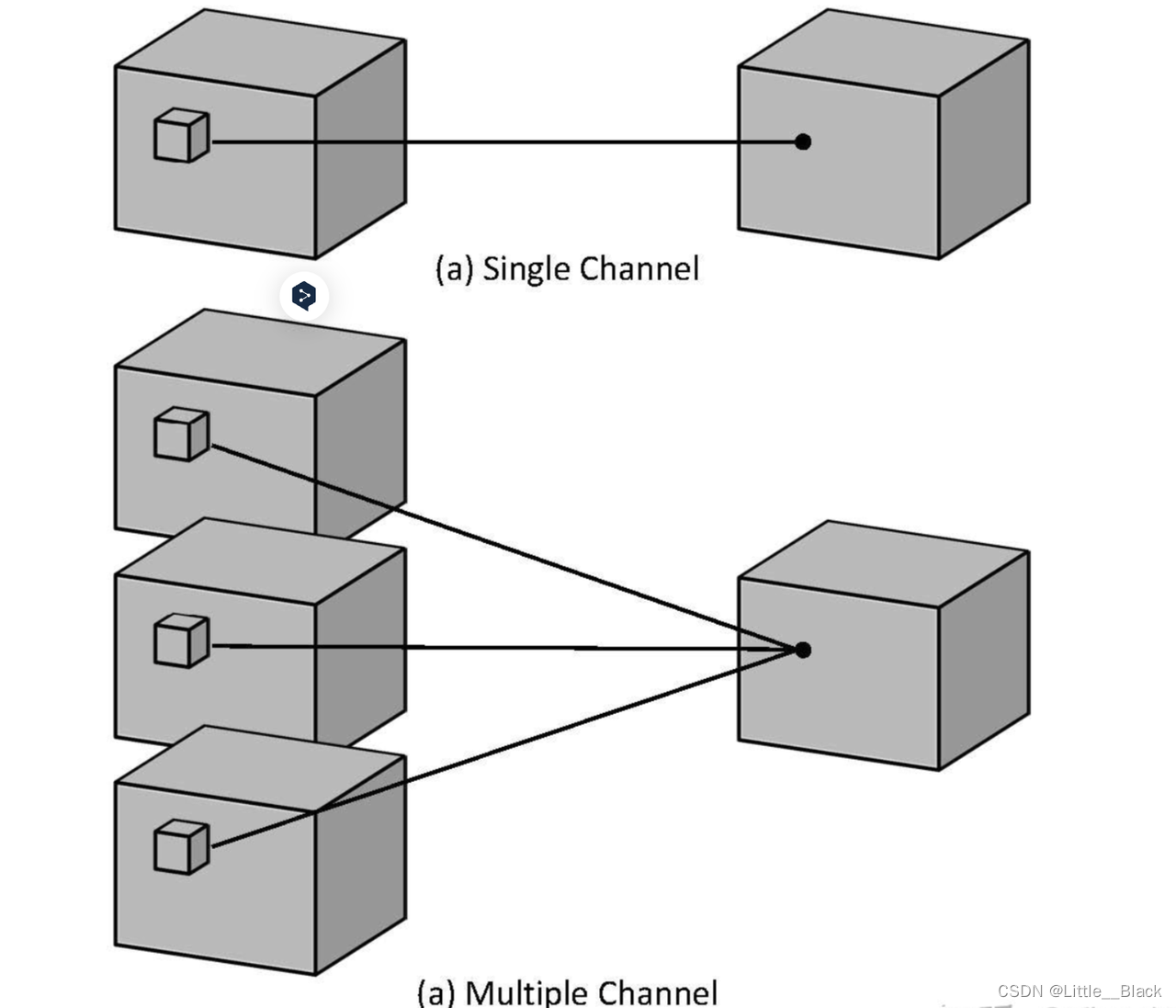
针对单通道,与2D卷积不同之处在于,输入图像多了一个 depth 维度,故输入大小为(1, depth, height, width),卷积核也多了一个k_d维度,因此卷积核在输入3D图像的空间维度(height和width维)和depth维度上均进行滑窗操作,每次滑窗与 (k_d, k_h, k_w) 窗口内的values进行相关操作,得到输出3D图像中的一个value.
针对多通道,输入大小为(3, depth, height, width),则与2D卷积的操作一样,每次滑窗与3个channels上的 (k_d, k_h, k_w) 窗口内的所有values进行相关操作,得到输出3D图像中的一个value。
2.1 原理简介
使用两个或多个从不同角度拍摄的2D图像来估计每个像素的深度,从而重建3D场景。.一般而言,立体视觉系统需要有两个(或者两个以上)摄像头的支持,也就正如人类的双眼一样。
2.2 单目视觉
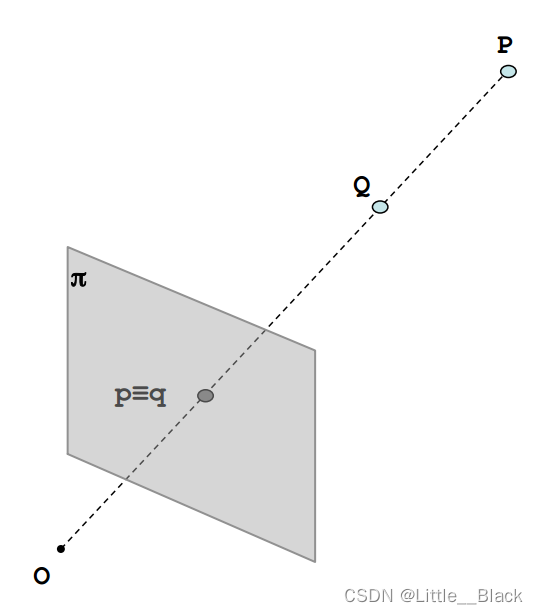
O点为相机的光心,π是摄像头的成像平面。
从图中可以看出,如果P点与Q点在同一条直线上,那么他们在图像上的成像点就是同一个点,也就是 p ≡ q p \equiv q p≡q ,那么也就看不出来他们在距离上的差异(也就无法知道Q在前还是P在前)。
2.3 双目视觉
正是在发现了单目系统的缺陷之后,我们将系统由一个摄像头增加到两个摄像头,这样也就构成了一个立体系统。如果我们可以在两幅图像中找到对应点,我们就可以通过三角测量的方法来求得深度
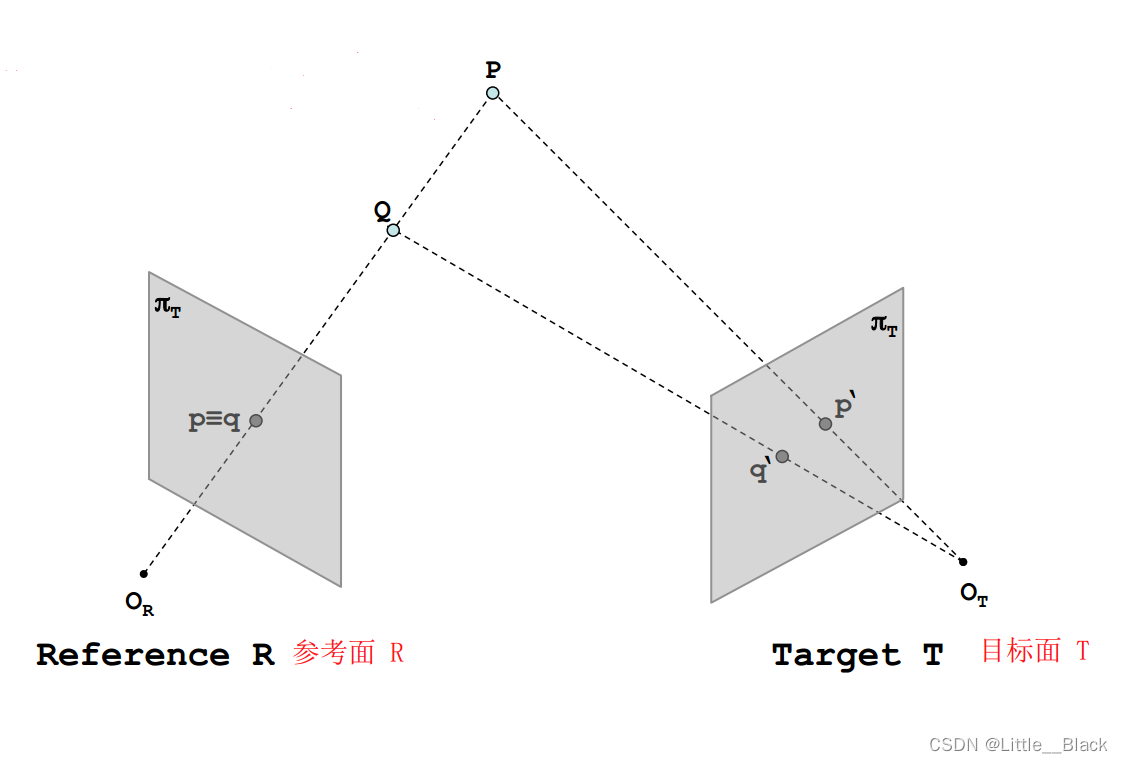
从图中可以很明显的看出,在增加了一个摄像头之后,P与Q在目标面T上的成像不在位于同一个点,而是有自己分别的成像点,也就是 q ′ q^{'} q′ 与 p ′ p^{'} p′。
那么,在我们给出了Reference与Target之后,我们应该如何解决参考面与目标面之间的对应关系呢?
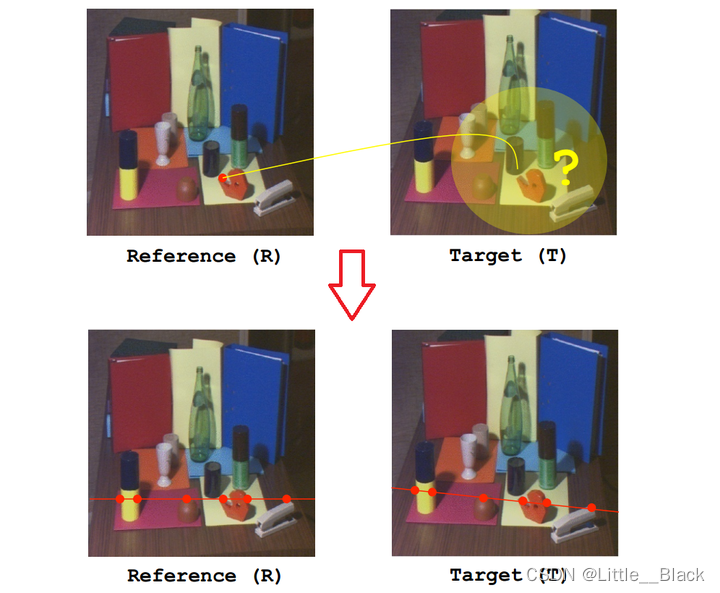
这个时候,就需要对极约束(极线约束),对极约束意味着一旦我们知道了立体视觉系统的对极几何之后,对两幅图像间匹配特征的二维搜索就转变成了沿着极线的一维搜索。
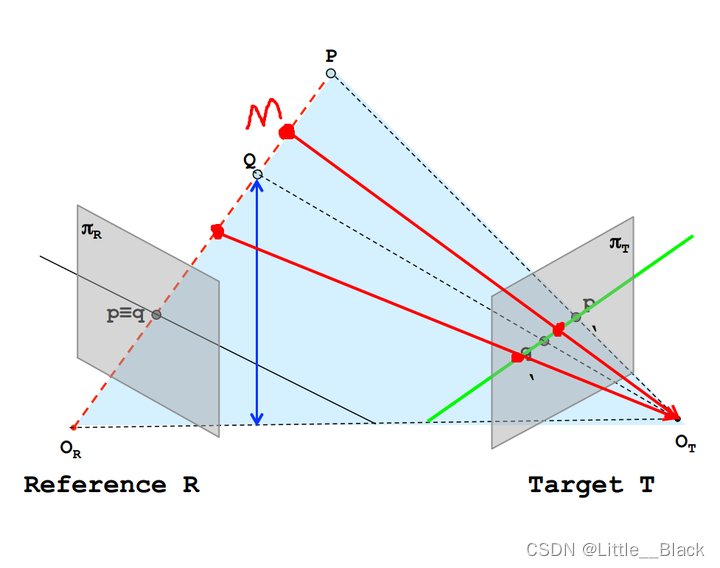
图中黑色实线为R平面一条极线,绿色为T平面一条极线。给定一幅图像上的一个特征,它在另一幅图像上的匹配视图一定在对应的极线上(图中将P,Q视为特征,可以看到在T上的成像在绿色直线上)
通常我们使用的立体视觉系统都是比较标准的系统,如图所示:
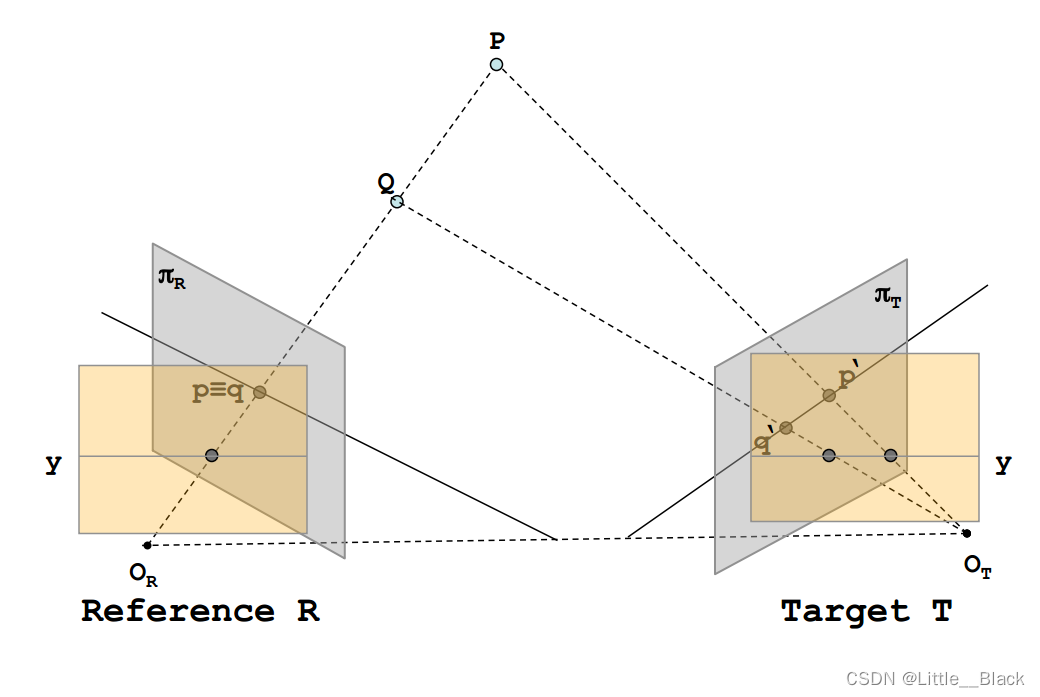
一旦我们知道了对应点的搜索区域,就可以将其从2D降到1D,这样就形成了更加方便的立体视觉,对应点都被约束再同一条极线上,也就是图中的y直线。下面给出一个实际的示例(在理想情况下,我们希望两个摄像头的参数是完全一致的,并且两个相机的位置是平行的)。
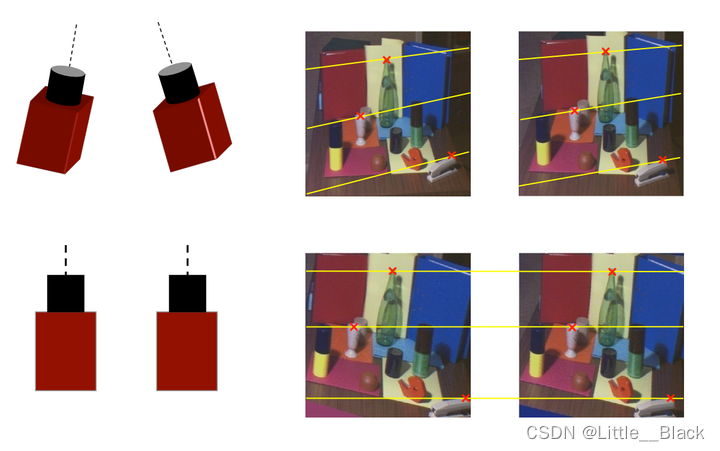
2.4 视差和深度计算原理
在我们已经确保两个摄像头的参数是完全一致的,并且两者的位置是平行之后,我们的关注点就落到了如何计算物体的深度信息,这也是最重要最关键的地方。下面给出的是标准立体视觉系统下的计算原理。
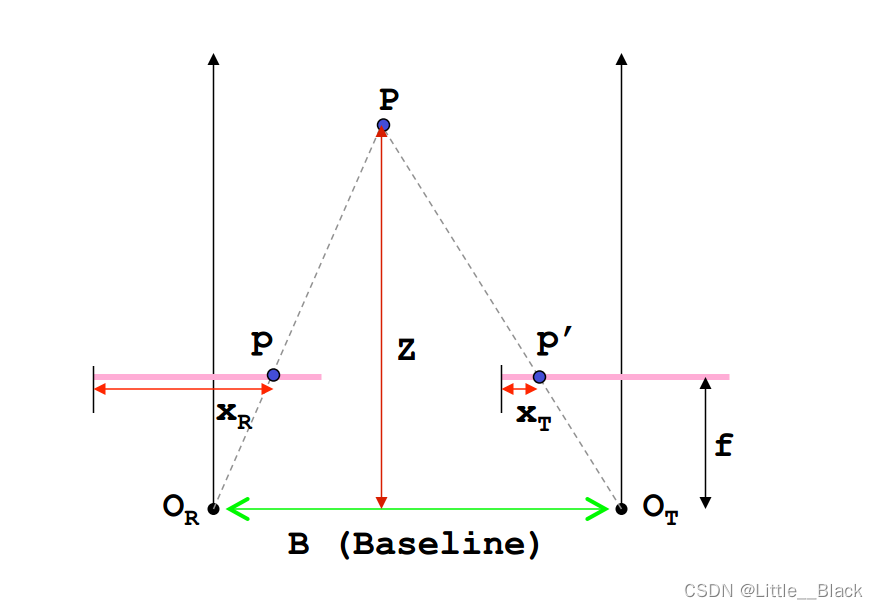
假设 P P P 为空间中的一点, O R O_R OR为左边摄像头的光心, O T O_T OT为右边摄像头的光心,摄像头的焦距为 f f f(光心到成像平面的距离),成像平面在图中用粉色线表示, B B B表示两个摄像头光心之间的距离,也称为基线, P P P在左右两个摄像机成像平面上的成像点分别为 p p p与 p ′ p' p′, x R x_R xR与 x T x_T xT为成像点的水平方向距离(通常我们得到的是像素坐标系下的 x x x左边,其单位为像素,因此需要转换为实际的物理长度,涉及到坐标系转换问题), Z Z Z就是我们需要求的深度。
根据三角形相似定理( Δ P p p ′ \Delta Ppp' ΔPpp′~ Δ P O R O T \Delta PO_RO_T ΔPOROT):
B Z = B − ( x R − x T ) Z − f \frac{B}{Z}=\frac{B-(x_R-x_T)}{Z-f} ZB=Z−fB−(xR−xT)===> Z = B ⋅ f x R − x T = B ⋅ f D Z=\frac{B\cdot f}{x_R-x_T}=\frac{B\cdot f}{D} Z=xR−xTB⋅f=DB⋅f
其中 D = x R − x T D = x_R-x_T D=xR−xT 就是我们通常所说的视差(disparity)。
我们可以发现,深度Z是跟视差D成反比关系的,当视差D越小时,Z越大,物体离立体视觉系统也就越远, 当视差D越大,Z越小,物体离立体视觉系统也就越近。这一点和我们人眼系统是一样的,当我们观察离我们比较近的物体的时候,视差很大,可以获得的信息也就越多,当物体离我们很远的时候,视差很小,我们获得的信息也就很少了。
在图像处理中,我们通常用灰度值来表示视差信息,视差越大,其灰度值也就越大,在视差图像的视觉效果上表现出来就是图像越亮,物体离我们越远,其视差越小,灰度值也越小,视差图像也就越暗。
2.5 深度估计
- 工作原理:使用深度学习模型来预测2D图像中每个像素的深度
- 优势:可以从单个2D图像中获得3D深度信息
- 应用:增强现实、虚拟现实、3D重建
3.1
世界坐标系 —> 相机坐标系 —> 投影矩阵 —> 像素映射 —> 生成图片
- 世界坐标系和相机坐标系转换可以通过dcm矩阵计算求出:
def dcm(origin: np.ndarray, target: np.ndarray):"""3 * 3 矩阵 ,{x,y,z}T 将origin坐标系转换到target坐标系的dcm旋转矩阵Args:origin:target:Returns:"""matrix = np.zeros((3, 3))for i in range(3):for j in range(3):matrix[i, j] = np.dot(target[i], origin[j])return matrix.T
- 投影矩阵,可以参考pyrender.camera.py中的透视投影和正交投影矩阵,也可以根据自己的需求定制
- 通过前两步计算出2d投影点,会落在(-1, 1)范围内,通过像素映射完成3d点到2d点的投影
完整代码:
class Camera:def __init__(self, scale, translation, resolution, znear=0.05, zfar=1000):self.scale = np.array(scale) # 相机缩放self.translation = np.array(translation) # 相机位移self.resolution = np.array(resolution) # 2d 分辨率self.znear = znear # 近平面self.h_s = self.resolution / 2 # h/2 w/2self.center = self.h_s # 2d投影面中心点def camera_matrix(self):"""相机外参矩阵,世界坐标系转相机坐标系Returns:"""world = np.eye(3)camera = np.eye(3)camera[-1, -1] = -1matrix = np.eye(4)matrix[:3, :3] = dcm(world, camera)return matrixdef get_projection_matrix(self) -> np.ndarray:"""投影矩阵 业务定制Returns:"""P = np.eye(4)P[0, 0] = self.scale[0]P[1, 1] = self.scale[1]P[0, 3] = self.translation[0] * self.scale[0]P[1, 3] = -self.translation[1] * self.scale[1]P[2, 2] = -1return Pclass Render:def __init__(self, camera: Camera):self.camera = cameradef p_point(self, point: np.ndarray):"""投影点坐标Args:point: 点 4D 例如[0.5,0.5,0.5,1] 3d点需要填充1Returns:"""p = self.camera.get_projection_matrix().dot(self.camera.camera_matrix().dot(point)) p = p[:2] / p[-1] * self.camera.h_s * np.array([1, -1]) + self.camera.centerreturn p
3.2 2.5D表示:
2D、2.5D和3D是描述物体和场景在空间中表示的三种方式,2D(平面)与3D(立体)又称为二维和三维,他们之间的区别是:2D你只能看到一个面,3D你能看到所有的面。
- 定义:
- 2D(二维):在2D中,物体或场景只有长度和宽度两个维度,常见的2D表示有图片、图画和屏幕上的图像
- 2.5D(二点五维):介于2D和3D之间,它通常描述的是一个场景从特定角度的深度信息,一个2.5D图像(例如深度图)为每个像素提供了一个深度值。
- 3D(三维):3D表示考虑了长度、宽度和深度,它为场景中的每个点提供了完整的三维坐标,常见的3D表示包括3D模型、点云等。
- 区别:
- 维度和信息完整性:2D缺乏深度信息;2.5D提供了从某个视角的深度信息;3D提供了完整的三维坐标信息。
- 视角依赖性:2.5D通常与特定的视角相关,而3D表示是视角无关的
- 数据复杂性:2D数据最简单,只需要x和y坐标;2.5D需要x、y和深度;3D需要x、y和z三个坐标。
- 联系:
- 从2D到2.5D: 如果你有一个2D图像和与之相关的深度信息,你可以得到一个2.5D表示。例如,使用深度相机如Kinect可以得到深度图。
- 从2D到3D: 通过多个2D图像和某种形式的结构从运动或立体视觉,你可以重建出3D场景或物体。但这比从2.5D到3D更为复杂。
- 从2.5D到3D: 从深度图中可以重建3D信息,例如生成一个点云。但由于2.5D信息通常是从一个视角获得的,因此可能不能完全恢复物体或场景的所有3D信息。
- 简而言之,2D、2.5D和3D代表了逐渐增加的空间信息和复杂性。2.5D是一个中间表示,提供了比2D更多的深度信息,但没有3D那么完整。
- 2D与2.5D的关系可以看成X轴与Y轴旋转了指定的角度后形成的新的屏幕
-
坐标旋转算法:
-
-
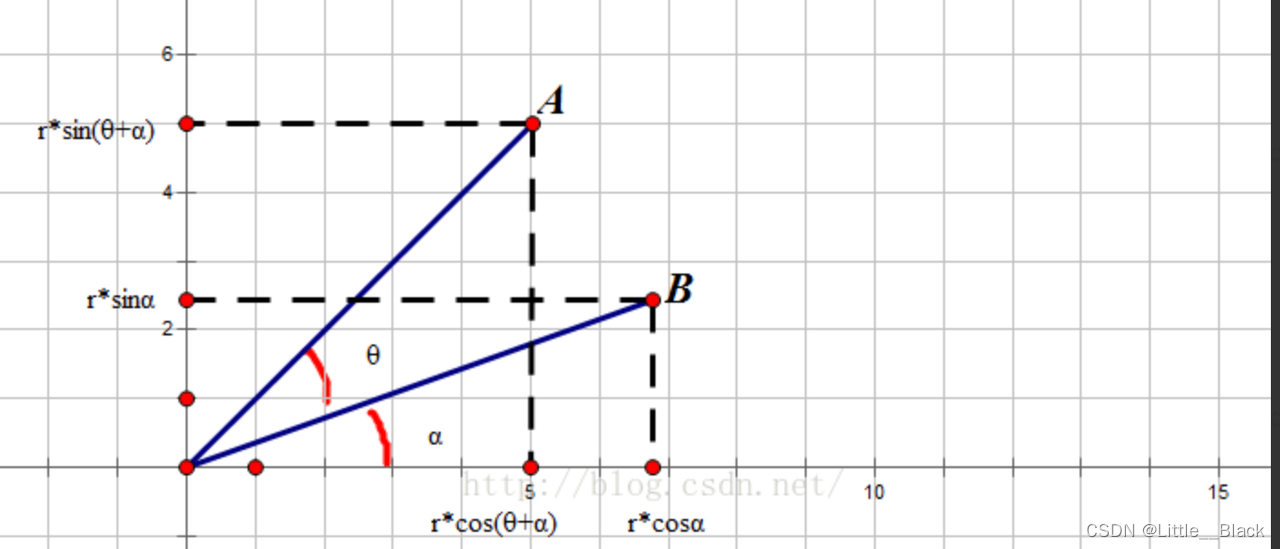
根据三角函数公式:
-
sin ( A + B ) = sin A ∗ cos B + sin B ∗ cos A \sin(A+B) = \sin A * \cos B + \sin B * \cos A sin(A+B)=sinA∗cosB+sinB∗cosA
-
cos ( A + B ) = cos A ∗ cos B − sin A ∗ sin B \cos(A+B)=\cos A * \cos B - \sin A * \sin B cos(A+B)=cosA∗cosB−sinA∗sinB
-
线段由 B O BO BO转到 A O AO AO,旋转后的坐标计算公式如下:
-
( x , y ) [ c o s θ s i n θ − s i n θ c o s θ ] = ( x ∗ c o s θ − y ∗ s i n θ , x ∗ s i n θ + y ∗ c o s θ ) (x,y) \left[ \begin{matrix} cos\theta &sin\theta \\ -sin\theta & cos\theta \end{matrix} \right]=(x*cos\theta-y*sin\theta, x*sin\theta+y*cos\theta) (x,y)[cosθ−sinθsinθcosθ]=(x∗cosθ−y∗sinθ,x∗sinθ+y∗cosθ)
-
通过矩阵的知识可以知道,X轴的基向量为[1,0];Y轴的基向量为[0,1]。有X和Y轴基向量组成的矩阵是一个单位矩阵。所以常规的平面直角坐标系的任何一点可以表示为:
( x , y ) [ 1 0 0 1 ] = ( x 1 , y 1 ) (x,y)\left[ \begin{matrix} 1 &0 \\ 0 & 1 \end{matrix} \right]=(x1, y1) (x,y)[1001]=(x1,y1)
为了将2D坐标映射到2.5D坐标,需要定义2.5D坐标系统使用的基向量。因为2.5D坐标系实际上是通过旋转X与Y轴实现的,所以通过旋转算法和上面的单位矩阵,可以得到新坐标系的X和Y轴基向量:
[ 1 0 0 1 ] [ c o s θ s i n θ − s i n α c o s α ] = [ c o s θ s i n θ − s i n α c o s α ] \left[ \begin{matrix} 1 &0 \\ 0 & 1 \end{matrix} \right]\left[ \begin{matrix} cos\theta &sin\theta \\ -sin\alpha & cos\alpha \end{matrix} \right]=\left[ \begin{matrix} cos\theta &sin\theta \\ -sin\alpha & cos\alpha \end{matrix} \right] [1001][cosθ−sinαsinθcosα]=[cosθ−sinαsinθcosα]
可以看出,将2D坐标系中的基向量转换为2.5D坐标系统的基向量时,结果其实就是旋转矩阵本身,这个旋转矩阵就是2.5D坐标系中的X和Y轴基向量。
注意:这里分别使用θ和α,是因为X和Y轴可以旋转不同的角度。如果 θ+α=90度,那么Sin(α)=Cos( θ );Cos(α)=Sin( θ )。上面的矩阵可以被替换为:
[ c o s θ s i n θ − c o s θ s i n θ ] \left[ \begin{matrix} cos\theta &sin\theta \\ -cos\theta & sin\theta \end{matrix} \right] [cosθ−cosθsinθsinθ]
现在定义2D坐标系为W(x,y),2.5D坐标系为G(x,y)。2D坐标系的X轴相对于2.5D坐标系X轴顺时针旋转30°,Y轴旋转60°。通过上面的公式可以得到W(x,y)对应的G(x,y):
G x = ( W x − W y ) ∗ c o s θ G_x = (W_x-W_y) * cos\theta Gx=(Wx−Wy)∗cosθ
G y = ( W x + W y ) ∗ s i n θ G_y = (W_x+W_y) * sin\theta Gy=(Wx+Wy)∗sinθ
2.5D坐标只需利用上面的工作进行逆运算就能得到:
W x = ( G x ∗ s i n θ + G y ∗ c o s θ ) / 2 ∗ s i n θ ∗ c o s θ W_x = (G_x*sin\theta+G_y*cos\theta)/2*sin\theta*cos\theta Wx=(Gx∗sinθ+Gy∗cosθ)/2∗sinθ∗cosθ
W y = ( G y ∗ c o s θ − G x ∗ s i n θ ) / 2 ∗ s i n θ ∗ c o s θ W_y = (G_y*cos\theta-G_x*sin\theta)/2*sin\theta*cos\theta Wy=(Gy∗cosθ−Gx∗sinθ)/2∗sinθ∗cosθ
4.1 多视图网络
- 工作原理:使用从不同角度的多个2D视图的信息来提取3D特征。
- 应用:3D物体识别、3D重建。
- 优点:能够从不同的2D视图中捕获3D信息。
4.2 融合2D和3D特征
- 工作原理:将2D图像特征与3D数据特征(例如点云)结合起来。
- 应用:3D物体检测、场景分割。
- 优点:利用了2D图像和3D结构的强大信息。
相关文章:

自动驾驶之—2D到3D升维
前言: 最近在学习自动驾驶方向的东西,简单整理一些学习笔记,学习过程中发现宝藏up 手写AI 3D卷积 3D卷积的作用:对于2DCNN,我们知道可以很好的处理单张图片中的信息,但是其对于视频这种由多帧图像组成的图…...
ubuntu18.4(后改为20.4)部署chatglm2并进行基于 P-Tuning v2 的微调
下载驱动 NVIDIA显卡驱动官方下载地址 下载好对应驱动并放在某个目录下, 在Linux系统中安装NVIDIA显卡驱动前,建议先卸载Linux系统自带的显卡驱动nouveau。 禁用nouveau 首先,编辑黑名单配置。 vim /etc/modprobe.d/blacklist.conf 在文件的最后添加…...

爬虫-获取数据xpath
安装lxml pip3 install lxml基本用法 import reauests from lxml import etree url = xxx res = reuests.get(url).text html = etree.HTML(res) # 获取所有div标签 xpath = //div print(html.xpath(xpath)) #获取id=xx的div标签下的class=yy的span标签 xpath = //div[@id=&quo…...
SpringBoot中使用JdbcTemplate访问Oracle数据库
Oracle相信大家都不陌生吧,一个大型的数据库,至于数据库,我相信各位都比较熟悉了,一个软件系统,不论是我们常做的App、小程序、还是传统的web站点,我们都有用户的信息,相关业务的数据࿰…...
【Linux】权限完结
个人主页点击直达:小白不是程序媛 系列专栏:Linux被操作记 目录 前言 chown指令 chgrp指令 文件类型 file指令 目录的权限 粘滞位 umask指令 权限总结 前言 上篇文章我们说到对于一个文件所属者和所属组都是同一个人时,使用所属者身…...
)
计算机网络-应用层(3)
一、FTP 文件传输协议 (File Transfer Protocol,FTP) 简称为“文传协 议”,用于在Internet上控制文件的双向传输。 FTP 客户上传文 件时,通过服务器20号端口建立的连接是建立在TCP 之上的数 据连接,通过服务器21号端口建立的连接是建立在TCP 之上的控制连…...

虎去兔来(C++)
系列文章目录 进阶的卡莎C++_睡觉觉觉得的博客-CSDN博客数1的个数_睡觉觉觉得的博客-CSDN博客双精度浮点数的输入输出_睡觉觉觉得的博客-CSDN博客足球联赛积分_睡觉觉觉得的博客-CSDN博客大减价(一级)_睡觉觉觉得的博客-CSDN博客小写字母的判断_睡觉觉觉得的博客-CSDN博客纸币(…...

docker基础镜像定制
docker基础镜像定制 1 简言2.准备软件源文件sources.list3.制作基础镜像3.1 编写Dockerfile命令3.2 制作基础镜像k8sbase1.03.3 测试基础镜像1 简言 官方基础镜像一般自带的linux命令是比较少,tcpdump、telnet登等命令是没有的,这时,定制一套适合自己的基础镜像是必要的,在…...
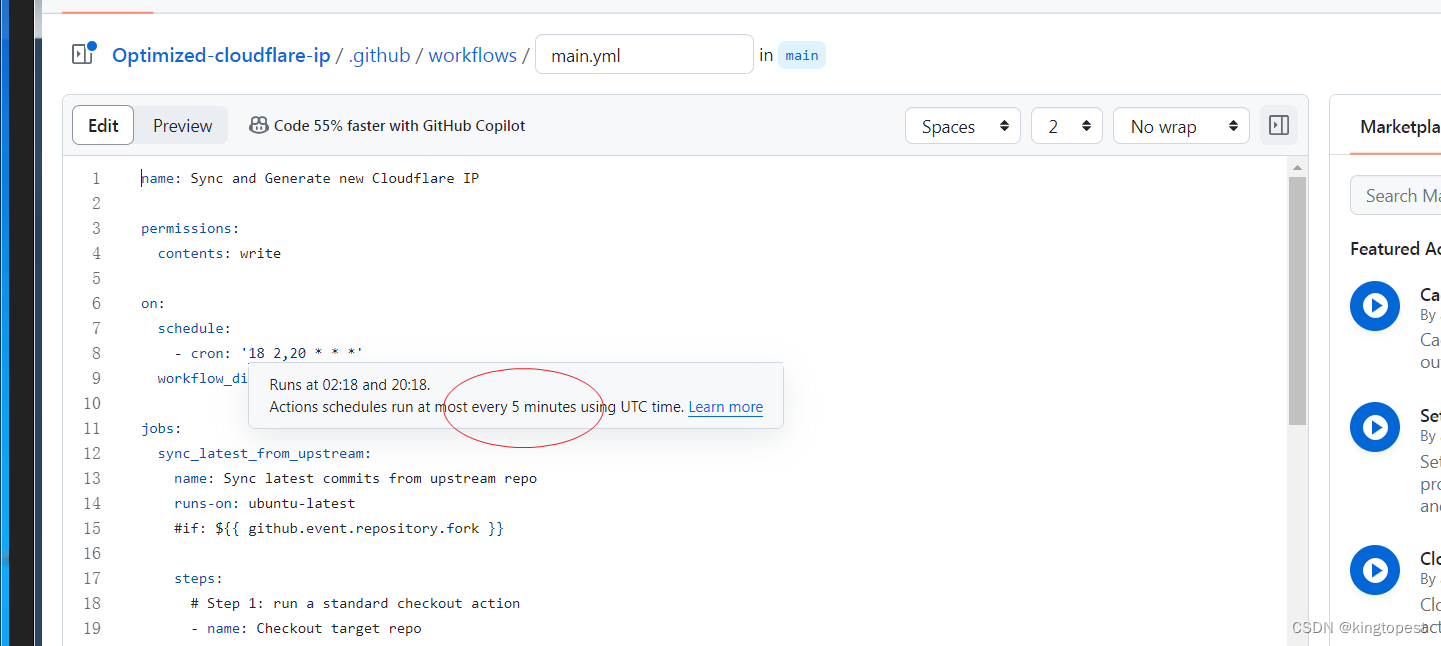
解决git action定时任务执行失败的方法
为了测试git action定时任务是否有效,你可能选择一个最近的时间测试, 但是发现怎么也触发不了,是不是觉得很苦恼。但是同样的时间,在第二天的定时任务又能成功运行。 这是什么原因? 原因就在上图,git act…...
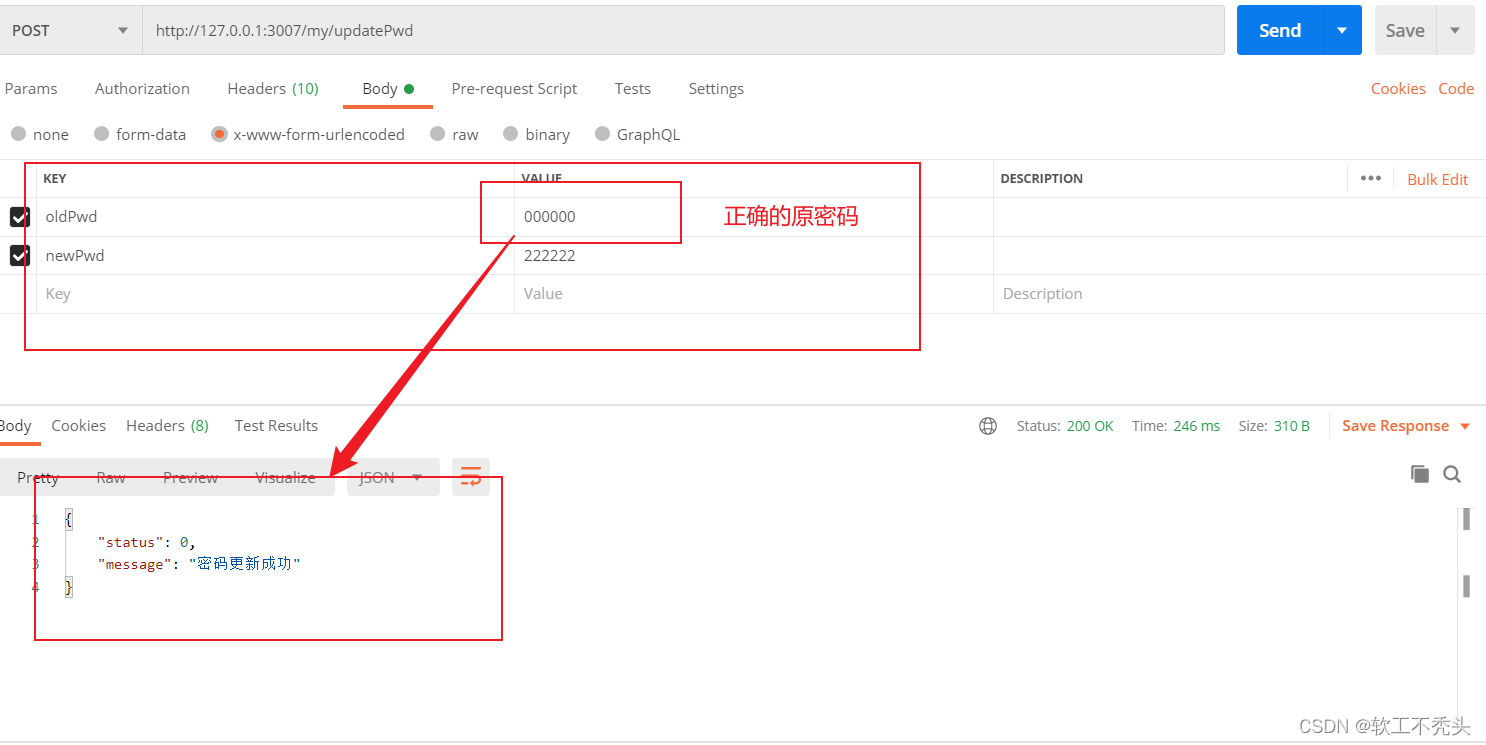
Node编写重置用户密码接口
目录 前言 定义路由和处理函数 验证表单数据 实现重置密码功能 前言 接前面文章,本文介绍如何编写重置用户密码接口 定义路由和处理函数 路由 // 重置密码的路由 router.post(/updatepwd, userinfo_handler.updatePassword) 处理函数 exports.updatePasswo…...
Day13力扣打卡
打卡记录 奖励最顶尖的 k 名学生(哈希表排序) 用哈希表对所有的positive与negative词条进行映射,然后遍历求解。tip:常用的分割字符串的操作:1.stringstream配合getline() [格式buf, string, char]2.string.find()[find未找到目标会返回npos…...

独立开发者知识贴
有一个github仓库,叫做独立开发变现周刊,很不错,作者能从21年能坚持更新到现在,我很佩服。 它里边有很多独立开发者成功的作品案例,我对这些很感兴趣。 在阅读时,我会问自己以下几个问题: 解…...

软考系列(系统架构师)- 2009年系统架构师软考案例分析考点
试题一 软件架构设计 【问题1】(9分) 软件质量属性是影响软件架构设计的重要因素。请用200字以内的文字列举六种不同的软件质量属性名称并解释其含义。 常见的软件质量属性有多种,例如性能(Performance)、可用性(Ava…...

C语言每日一题(21)删除排序数组中的重复项
力扣 26.删除排序数组中的重复项 题目描述 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考…...

如何快速解决d3dcompiler_43.dll缺失问题?五种方法快速解决
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“D3DCompiler_43.dll缺失”。这个错误通常会导致游戏、应用程序或系统无法正常运行。为了解决这个问题,我们需要采取一些修复方案来恢复缺失的文件。本文将介绍五个修复D3DCompi…...

mongodb数据迁移的方法
这个方法只能将数据从一个mongo数据库转移到另一个mongo数据库 这个命令可以备份mongo数据(mongo数据库中的数据备份转换为文件) mongodump --host HOST --port PORT --username USERNAME --password PASSWORD --db DB -c COLLECTION --out OUT这个命令…...
Spring MVC 中文文档
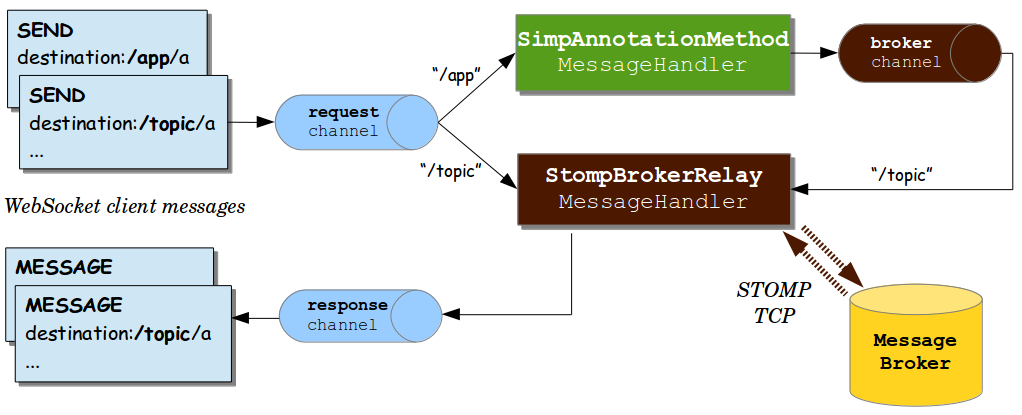
1. Spring Web MVC Spring Web MVC是建立在Servlet API上的原始Web框架,从一开始就包含在Spring框架中。正式名称 “Spring Web MVC” 来自其源模块的名称( spring-webmvc),但它更常被称为 “Spring MVC”。 与Spring Web MVC并…...
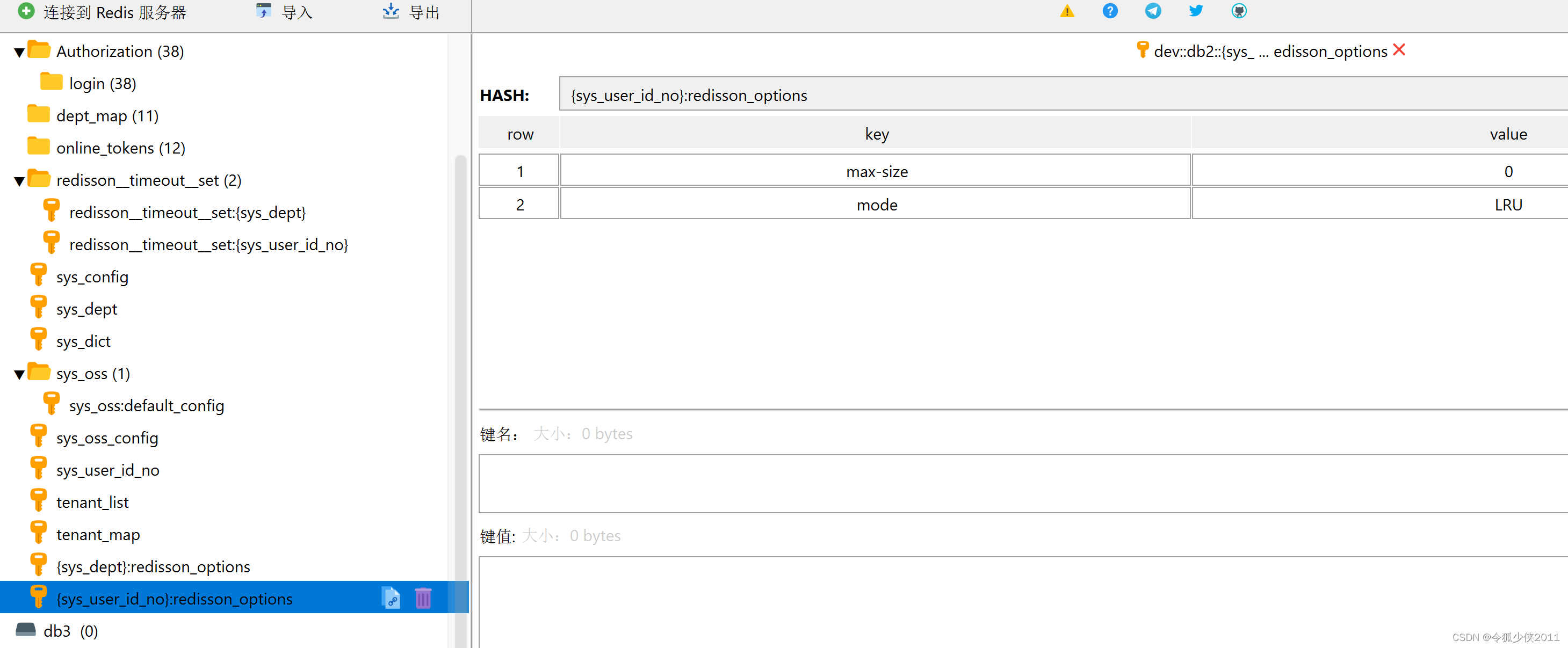
RedissonCach的源码流程
上: https://blog.csdn.net/Michelle_Zhong/article/details/126384566 中: https://blog.csdn.net/michelle_zhong/category_11874153.html 下: https://blog.csdn.net/Michelle_Zhong/article/details/126391915?ops_request_misc%257B%…...
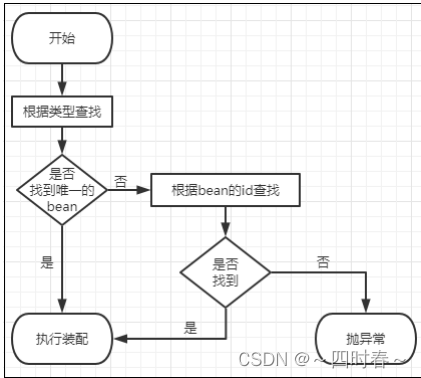
spring-基于注解管理bean
基于注解管理bean 一、标记与扫描1、引入依赖2、创建spring配置文件3、创建组件4、扫描组件4.1、基本扫描:4.2、指定要排除的组件4.3、仅扫描指定组件 二、基于注解的自动装配 一、标记与扫描 1、引入依赖 <dependencies> <!-- 基于Maven依赖传递性&…...
数据挖掘(7.1)--数据仓库
目录 引言 一、数据库 1.简介 2.数据库管理系统(DBMS) 二、数据仓库 数据仓库特征 数据仓库作用 数据仓库和DBMS对比 分离数据仓库和数据库 引言 数据仓库的历史可以追溯到20世纪60年代,当时计算机领域的主要工作是创建运行在主文件上的单个应用࿰…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...

【见合八方平面波导外腔激光器专题系列】用于干涉光纤传感的低噪声平面波导外腔激光器2
----翻译自Mazin Alalus等人的文章 摘要 1550 nm DWDM 平面波导外腔激光器具有低相位/频率噪声、窄线宽和低 RIN 等特点。该腔体包括一个半导体增益芯片和一个带布拉格光栅的平面光波电路波导,采用 14 引脚蝶形封装。这种平面波导外腔激光器设计用于在振动和恶劣的…...

SeaweedFS S3 Spring Boot Starter
SeaweedFS S3 Spring Boot Starter 源码特性环境要求快速开始1. 添加依赖2. 配置文件3. 使用方式方式一:注入服务类方式二:使用工具类 API 文档SeaweedFsS3Service 主要方法SeaweedFsS3Util 工具类方法 配置参数运行测试构建项目注意事项集成应用更多项目…...
