【Codeforces】 CF582D Number of Binominal Coefficients
题目链接
CF方向
Luogu方向
题目解法
看到 p α ∣ ( n k ) p^{\alpha} | \binom{n}{k} pα∣(kn) ,首先想到 k u m m e r kummer kummer 定理,那么限制即为 n − k n-k n−k 和 k k k 做加法在 p p p 进制下的进位数 ≥ α \ge \alpha ≥α
然后就是一个显然的数位 d p dp dp 了
因为进位从前往后数位 d p dp dp 不太好考虑,所以我们考虑从后往前做,然后多记录一维 0 / 1 / 2 0/1/2 0/1/2
我的状态是 f i , j , 0 / 1 , 0 / 1 / 2 f_{i,j,0/1,0/1/2} fi,j,0/1,0/1/2 表示后 i i i 位有 j j j 个进位(不包括第 i i i 位的),这一位是否进位,后面 i i i 位 n n n 与 A A A 的关系(0 表示 n < A n<A n<A,1 表示 n = A n=A n=A,2 表示 n > A n>A n>A)
因为我们把 n , k n,k n,k 变成了 n − k n-k n−k 和 k k k,所以天然保证了 n ≥ k n\ge k n≥k,不需要考虑 n , k n,k n,k 的大小关系
直接 d p dp dp 即可,实现的有些烦,但也不知道可以优化什么了
时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=4100,P=1e9+7;
int p,a,f[2][N][2][3];
LL A[N],B[N];
// int g[P];//g[i]表示a+b<=i的方案数(a,b无序)
char str[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void inc(int &x,LL y){ x=(x+y)%P;}
int g(int x){if(x<0) return 0;if(x<p) return (1ll*(x+2)*(x+1)/2)%P;x=p*2-1-x;x=1ll*p*p%P-(1ll*x*(x-1)/2)%P;return x<0?x+P:x;
}
int main(){p=read(),a=read();scanf("%s",str+1);int len=strlen(str+1);for(int i=1;i<=len;i++) A[i]=str[len-i+1]-48;int n=0;for(int i=len;i>=1;i--){for(int j=1;j<N;j++) B[j]*=10;B[1]+=A[i];for(int j=1;j<N;j++) if(B[j]>=p) B[j+1]+=B[j]/p,B[j]%=p;}for(int i=1;i<N;i++) A[i]=B[i];for(int i=1;i<N;i++) if(A[i]) n=i;reverse(A+1,A+n+1);f[(n+1)&1][0][0][1]=1;for(int i=n+1;i>1;i--){int c=A[i-1];int g_c=g(c);int g_c_1=g(c-1);int g_c_2=g(c-2);int g_p_1=g(p-1);int g_p_2=g(p-2);int g_p_c=g(p+c);int g_p_c_1=g(p+c-1);int g_p_c_2=g(p+c-2);int g_2p_2=g(p*2-2);int g_2p_3=g(p*2-3);memset(f[~i&1],0,sizeof(f[~i&1]));for(int j=0;j<=n-i+1;j++){//calc f[~i&1][j][0][0]inc(f[~i&1][j][0][0],1ll*f[i&1][j][0][0]*g_c);if(c){for(int t:{1,2}) inc(f[~i&1][j][0][0],1ll*f[i&1][j][0][t]*g_c_1);if(j){inc(f[~i&1][j][0][0],1ll*f[i&1][j-1][1][0]*g_c_1);if(c>1) for(int t:{1,2}) inc(f[~i&1][j][0][0],1ll*f[i&1][j-1][1][t]*g_c_2);}}//calc f[~i&1][j][0][1]if(!c) inc(f[~i&1][j][0][1],1ll*f[i&1][j][0][1]*g_c);else inc(f[~i&1][j][0][1],1ll*f[i&1][j][0][1]*(g_c-g_c_1+P));if(j&&c) inc(f[~i&1][j][0][1],1ll*f[i&1][j-1][1][1]*(g_c_1-g_c_2+P));//calc f[~i&1][j][0][2]for(int t:{0,1}) inc(f[~i&1][j][0][2],1ll*f[i&1][j][0][t]*(g_p_1-g_c+P));inc(f[~i&1][j][0][2],1ll*f[i&1][j][0][2]*(g_p_1-g_c_1+P));if(j){for(int t:{0,1}) inc(f[~i&1][j][0][2],1ll*f[i&1][j-1][1][t]*(g_p_2-g_c_1+P));inc(f[~i&1][j][0][2],1ll*f[i&1][j-1][1][2]*(g_p_2-g_c_2+P));}//calc f[~i&1][j][1][0]inc(f[~i&1][j][1][0],1ll*f[i&1][j][0][0]*(g_p_c-g_p_1+P));for(int t:{1,2}) inc(f[~i&1][j][1][0],1ll*f[i&1][j][0][t]*(g_p_c_1-g_p_1+P));if(j){inc(f[~i&1][j][1][0],1ll*f[i&1][j-1][1][0]*(g_p_c_1-g_p_2+P));for(int t:{1,2}) inc(f[~i&1][j][1][0],1ll*f[i&1][j-1][1][t]*(g_p_c_2-g_p_2+P));}//calc f[~i&1][j][1][1]inc(f[~i&1][j][1][1],1ll*f[i&1][j][0][1]*(g_p_c-g_p_c_1+P));if(j) inc(f[~i&1][j][1][1],1ll*f[i&1][j-1][1][1]*(g_p_c_1-g_p_c_2+P));//calc f[~i&1][j][1][2]for(int t:{0,1}) inc(f[~i&1][j][1][2],1ll*f[i&1][j][0][t]*(g_2p_2-g_p_c+P));inc(f[~i&1][j][1][2],1ll*f[i&1][j][0][2]*(g_2p_2-g_p_c_1+P));if(j){for(int t:{0,1}) inc(f[~i&1][j][1][2],1ll*f[i&1][j-1][1][t]*(g_2p_2-g_p_c_1+P));inc(f[~i&1][j][1][2],1ll*f[i&1][j-1][1][2]*(g_2p_2-g_p_c_2+P));}}}int ans=0;for(int i=a;i<=n;i++) inc(ans,1ll*f[1][i][0][0]+f[1][i][0][1]);printf("%d\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}
/*
f[i][j][0/1][0/1/2]:到第i位,后j位已经填好且进位了j次,这一位是否进位,n后面j位和A的关系(0小于,1等于,2大于)
*/相关文章:

【Codeforces】 CF582D Number of Binominal Coefficients
题目链接 CF方向 Luogu方向 题目解法 看到 p α ∣ ( n k ) p^{\alpha} | \binom{n}{k} pα∣(kn) ,首先想到 k u m m e r kummer kummer 定理,那么限制即为 n − k n-k n−k 和 k k k 做加法在 p p p 进制下的进位数 ≥ α \ge \alpha ≥α …...
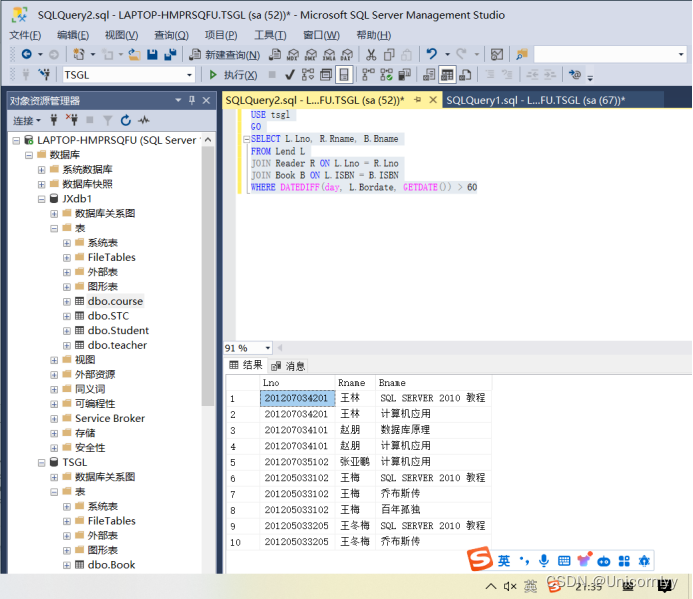
sql第二次上机作业
1查找借阅了ISBN为“4-6045-1023-4”的借书证号,读者姓名,专业名和借书时间 use tsgl go select Reader.Lno,Rname,Spec,Lend.Bordate FROM Reader,Lend WHERE Reader.LnoLend.Lno AND ISBN 4-6045-1023-42查找借阅了《数据库原理》一书的借阅信息&…...
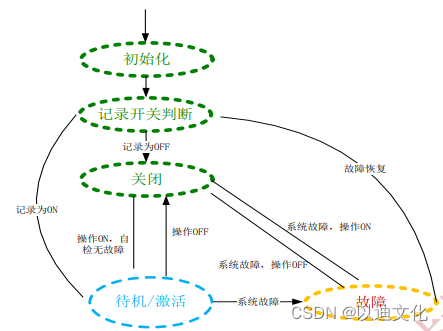
辅助驾驶功能开发-功能规范篇(22)-3-L2级辅助驾驶方案功能规范
1.3.3 TLA系统功能定义 1.3.3.1 状态机 1.3.3.2 状态迁移图 1.3.3.3 功能定义 1.3.3.3.1 信号需求列表 1.3.3.3.2 系统开启关闭 1)初始化 车辆上电后,交通灯辅助系统(TLA)进行初始化,控制器需在 220ms 内发出第一帧报文,并在 3s 内完成内部自检,同时上电 3s 内不进行…...
)
Python基础入门例程16-NP16 发送offer(列表)
目录 描述 输入描述: 输出描述: 解答 : 说明: 描述 某公司在面试结束后,创建了一个依次包含字符串 Allen 和 Tom 的列表offer_list,作为通过面试的名单。 请你依次对列表中的名字发送类似 Allen, you…...

Web前端面试之Vue—对Vue的理解
目录 一、web发展历程 二、vue是什么 三、Vue核心特性 组件化 数据驱动 指令 四、Vue与Angular以及React的区别 一、web发展历程 Web是World Wide Web的简称,中文译为万维网 我们可以将它规划成如下的几个时代来进行理解 静态网页:最早的网页是没…...

C/C++晶晶赴约会 2020年12月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C晶晶赴约会 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C晶晶赴约会 2020年12月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 晶晶的朋友贝贝约晶晶下周一起去看展览࿰…...

js 解决 H 指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。 根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发…...

在JS中,var 、let 、const 总结
let是英文单词"let"的缩写。在JavaScript中,let 关键字用来声明一个块级作用域 的变量,这意味着变量仅在声明它的代码块内有效,超出该代码块作用域时就无法访问该变量。与var不同的是,let不会被提升到函数作用域或全局作…...
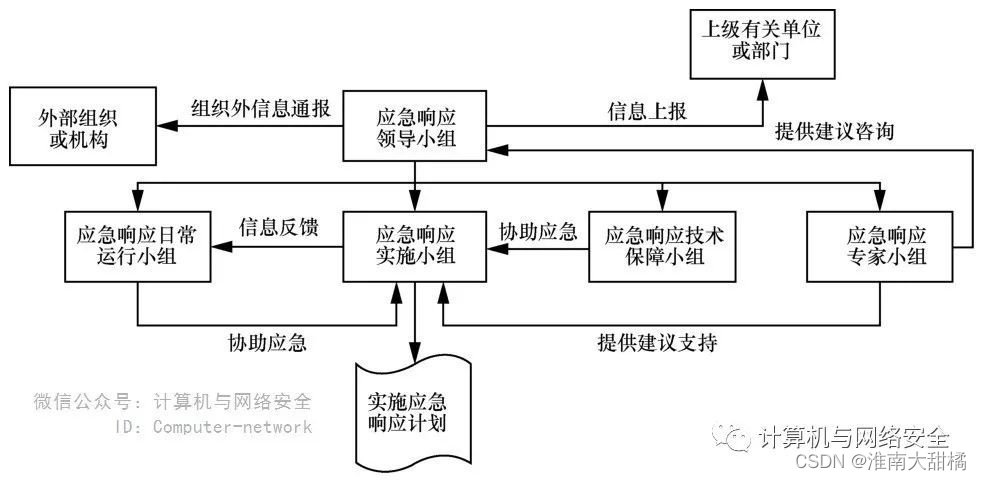
关于网络安全运营工作与安全建设工作的一些思考
以下内容是个人成长过程中对于网络安全运营工作的理解和思考,希望通过这篇文章帮助大家更好的去做安全运营体系化建设,开始吧! 文章目录 一、网络安全运营是什么?二、网络安全运营建设阶段第一阶段:设备限制阶段第二阶…...

【机器学习可解释性】4.SHAP 值
机器学习可解释性 1.模型洞察的价值2.特征重要性排列3.部分依赖图4.SHAP 值5.SHAP 值 高级使用 正文 理解各自特征的预测结果? 介绍 您已经看到(并使用)了从机器学习模型中提取一般解释技术。但是,如果你想要打破模型对单个预测的工作原理? SHAP 值…...

OpenCV官方教程中文版 —— 直方图均衡化
OpenCV官方教程中文版 —— 直方图均衡化 前言一、原理二、 OpenCV 中的直方图均衡化三、 CLAHE 有限对比适应性直方图均衡化 前言 本小节我们要学习直方图均衡化的概念,以及如何使用它来改善图片的对比。 一、原理 想象一下如果一副图像中的大多是像素点的像素值…...
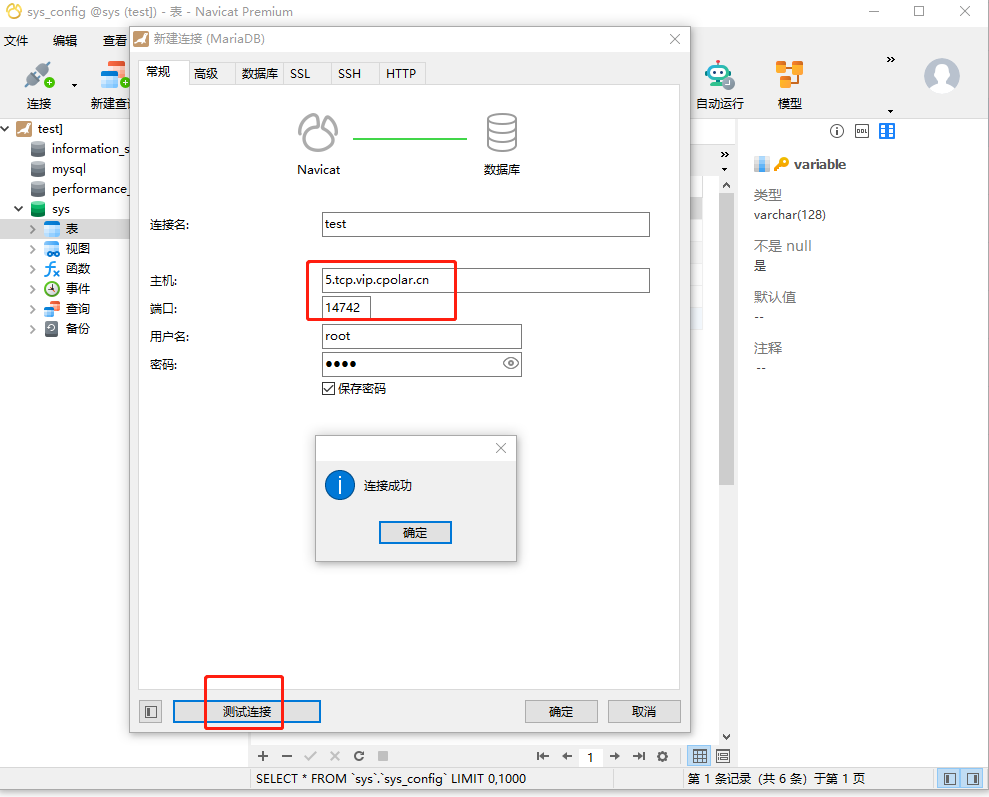
如何使用navicat图形化工具远程连接MariaDB数据库【cpolar内网穿透】
公网远程连接MariaDB数据库【cpolar内网穿透】 文章目录 公网远程连接MariaDB数据库【cpolar内网穿透】1. 配置MariaDB数据库1.1 安装MariaDB数据库1.2 测试局域网内远程连接 2. 内网穿透2.1 创建隧道映射2.2 测试随机地址公网远程访问3. 配置固定TCP端口地址3.1 保留一个固定的…...

【uniapp】uview1.x使用upload上传图片
和2.x不同的是,要用 action 来配置后端上传图片的接口地址; 再来一些配置项的命名有所不同,一般1.x的命名用 -,2.x的命名使用小驼峰; 1.x 的上传会自带删除时的提示框,2.x 没有; 重要的几个配置…...
基于nodejs+vue食力派网上订餐系统
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

软件测试常用的8种功能测试类型有哪些?
软件测试常用的8种功能测试类型有哪些? 单元测试 单元测试确保在一个段中编写的每一段代码都能产生最佳结果。开发人员在单元测试期间只看接口和确定部件。它提供了代码进展的文档,因为每个代码单元在继续下一个之前都经过了彻底的测试。 集成测试 至少对…...

动态规划之01背包问题
01背包问题 1. 【模板】01背包2. 分割等和子集3. 目标和4. 最后一块石头的重量 II 01背包问题是一种动态规划问题,用于求解在有限容量的背包中装入最大价值的物品组合。具体步骤如下: 定义一个二维数组dp[i][j],表示从前i个物品中选择若干个…...
安防监控项目---boa服务器的移植
文章目录 前言一、boa服务器简介二、移植步骤三、测试结果四、A9平台移植BOA总结 前言 书接上期,在配置完成环境后,那么接下来呢还得移植两个非常关键的东西,一个呢时boa服务器,另一个呢时cgi接口,boa服务器能够使得我…...

Gson 字符串常用转换方式(集合转换为Json数组
数组转换为 Json 字符串: GsonUtils.toJson(itemListBean.getImgs())json 字符串转换为数组 Gson().fromJson(goodsDbBean.getImgs(), String[].class)Json 转换为已知实体类 GsonUtils.parseJSON(result, AFileInfoBean.class);Json 转换为已知实体类集合 List<…...
)
MyBatis的使用(XML映射文件)
MyBatis的使用(XML映射文件) MyBatis基于注解开发简单便捷,但是弊端是失去SQL语句的灵活性,不能根据实际情况产生不同的SQL语句 MyBatis除了支持注解开发以外,还支持一种开发方式:XML映射文件,…...
localhost知识
文章目录 一、localhost是什么?二、localhost 在平时用到的地方三、 localhost 与 127.0.01 一、localhost是什么? localhost 是一个特殊的主机名,通常指代本机。它被用来进行本地开发和测试,也常被用作网络配置中的占位符&#…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
