【架构师】零基础到精通——康威定律
博客昵称:架构师Cool
最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。
作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟!
博主小留言:哈喽!各位CSDN的uu们,我是你的小弟Cool,希望我的文章可以给您带来一定的帮助
百万笔记知识库, 所有基础的笔记都在这里面啦,点击左边蓝字即可获取!助力每一位未来架构师!
欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
康威定律
- 康威定律
- 微服务利弊
康威定律
康威法则设计系统的组织,其产生的设计和架构,等价组织的组织架构
单块应用时代
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1yP9bSqH-1677399580856)(康威定律-单块应用.jpg)]
几个团队共同去对一个单块应用去开发和维护时,如果一个团队对这个单块应用进行改造引入一些新的功能或技术的时候,往往需要其他的团队协作和配合,连同做集成测试才能交付这个应用,这个时候,不仅仅是沟通协调成本高,团队和团队之间往往容易产生摩擦。也就是说,多团队之间和单应用产生不匹配,违反康威法则。怎么解决,微服务是一个解决的手段:
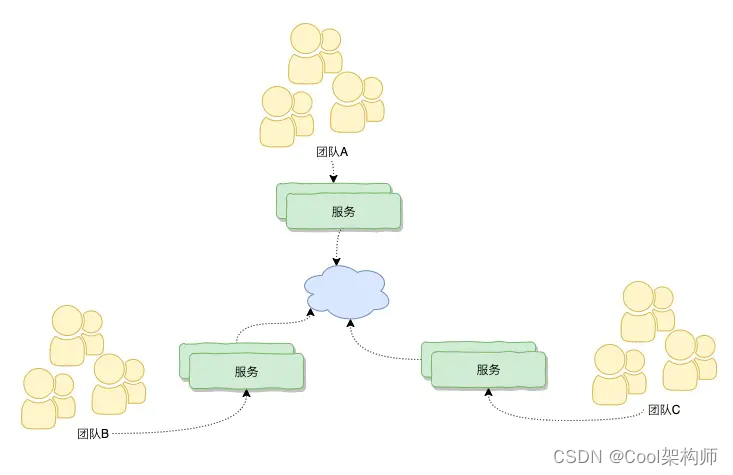
我们把单块的应用拆分成诺干个独立的应用,每个团队负责自己的服务,相互之间不干扰,当团队A服务的服务进行修改不需要其他的团队来配合,或者说这种配合沟通成本比较少,一般只发生在双方边界交集的地方,那么这个时候发现多团队和微服务之间架构的关系可以映射起来,它符合了康威法则,整体研发效率更高效。
微服务利弊
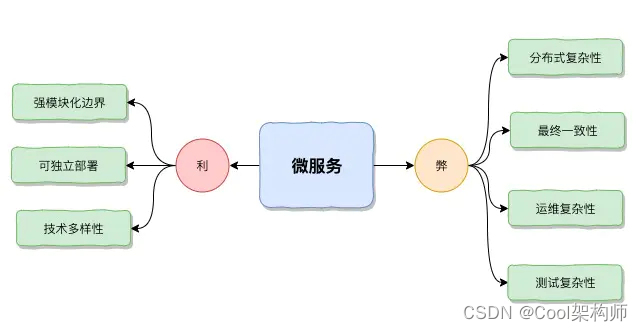
-
利
-
强模块化边界
我们知道做软件架构,软件设计,模块化是非常重要的一点,一开始我们写程序做软件,我们采用类的方式来做模块化,后面开始采用组件或类库的方式做模块化,可以做到工程上的重用和分享给其他团队来使用。微服务在组件的层次上面又高了一层,以服务的方式来做模块化,每个团队独立开始和维护自己的服务,有明显的一个边界,开发完一个服务其他团队可以直接调用这个服务,不需要像组件通过jar或源码的方式去进行分享,所以微服务的边界是比较清晰的。
-
可独立部署
可独立部署是微服务最显著的一个特性,每个团队可以根据自己的业务需求,当产品经理或业务方把需求提过来,可以根据需要独立开发和部署服务,一般来说不需要太过依赖其他团队去协同,这个对比单块应用,单块引用在这个方面需求很多团队来协助和帮忙。
-
技术多样性
微服务是分散式治理,没有集中治理,每个团队可以根据团队自己的实际情况和业务的实际情况去选择适合自己的技术栈,有些团队可能擅长Java开发,有些团队可能更偏向前端,更适合用nodejs去开发服务,不过这个不是越多越好,技术栈的引入也是有成本
-
-
弊
-
分布式复杂性
在原来单块应用就是一个应用,一个对单块应用的架构比较熟悉的人可以对整个单块应用有一个很好的把控。但是到了分布式系统,微服务化了以后可能涉及到的服务有好几十个,一些大公司可能涉及到的服务上百个,服务与服务之间是通过相互沟通来实现业务,那么这个时候整个系统就变成非常复杂,一般的开发人员或一个团队都无法理解整个系统是如何工作的,这个就是分布式带来的复杂性。
-
最终一致性
微服务的数据是分散式治理的,每个团队都有自己的数据源和数据拷贝,比方说团队A有订单数据,B团队也有订单数据,团队A修改了订单数据是否应该同步给团队B的数据呢,这里就涉及到数据一致性问题,如果没有很好的解决一致性问题,就可能造成数据的不一致,这个在业务上是不可以接受的。
-
运维复杂性
以往的运维需要管理的是机器+单块的应用,分布式系统和单块应用不一样的是,分布式系统需要很多的服务,服务与服务之间相互协同,那么对分布式系统的资源,容量规划,对监控,对整个系统的可靠性稳定性都非常具备挑战的。
-
测试复杂性
对测试人员来说,在单块应用上,一个测试团队只需要测试一个单块应用就可以了,到了分布式系统,各个服务是分布在各个团队的,这个对测试团队来说要求就很好,做集成测试的时候需要很多的团队相互配合去联合做集成测试。
-
相关文章:

【架构师】零基础到精通——康威定律
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...

Could not extract response: no suitable HttpMessageConverter
版本:spring-cloud-openfeign-core-2.1.1.RELEASE.jar,spring-webmvc-5.1.14.RELEASE.jar,jetty-server-9.4.41.v20210516.jar,tomcat-embed-core-9.0.48.jar 问题背景 生产服务请求下游服务时偶发抛出下面的异常,下…...

文献计量三大定律之一---洛特卡定律及普赖斯定律
科学生产率是洛特卡定律的基础,科学生产率”(Scientific Productivity))是指科学家(科研人员)在科学上所表现出的能力和工作效率,通常用其生产的科学文献的数量来衡量。 1926年,洛特卡在一篇论文中提出了科…...
2023年软考高级网络规划设计师
网络规划设计师是软考高级考试科目之一,也是比较难的科目,据官方数据统计网规每年的通过率很低,而且每年只有下半年11月份考一次,如果是直接裸考,估计很悬哦~ 但是你参加考试获得证书的过程就是一个学习网络规划系统知…...

数据治理驱动因素 -报考题
数据治理并不是到此为止,而是需要直接与企业战略保持一致。数据治理越显著地帮助解决组织问题,人们越有可能改变行为、接受数据治理实践。数据治理的驱动因素大多聚焦于减少风险或者改进流程。(1)减少风险1)一般性风险…...
2023淘宝天猫38节红包满减优惠活动时间是从几月几号什么时候开始?
2023年淘宝天猫38节活动将于2023年3月2日中午12点正式开始,活动将持续至2023年3月8日晚上23点59分。届时,淘宝天猫将推出一系列的优惠活动和红包福利,为广大女性用户送上节日的祝福和福利。在这个特别的节日里,淘宝天猫为女性用户…...
、数据压缩、存储优化)
Hive表优化、表设计优化、Hive表数据优化(ORC)、数据压缩、存储优化
文章目录Hive表优化Hive表设计优化分区表结构 - 分区设计思想分桶表结构 - Join问题Hive中的索引Hive表数据优化常见文件格式TextFileSequenceFileParquetORC数据压缩存储优化 - 避免小文件生成存储优化 - 合并输入的小文件存储优化 - ORC文件索引Row Group IndexBloom Filter …...

LearnOpenGL-入门-着色器
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录着色器GLSL数据类型输入与输…...
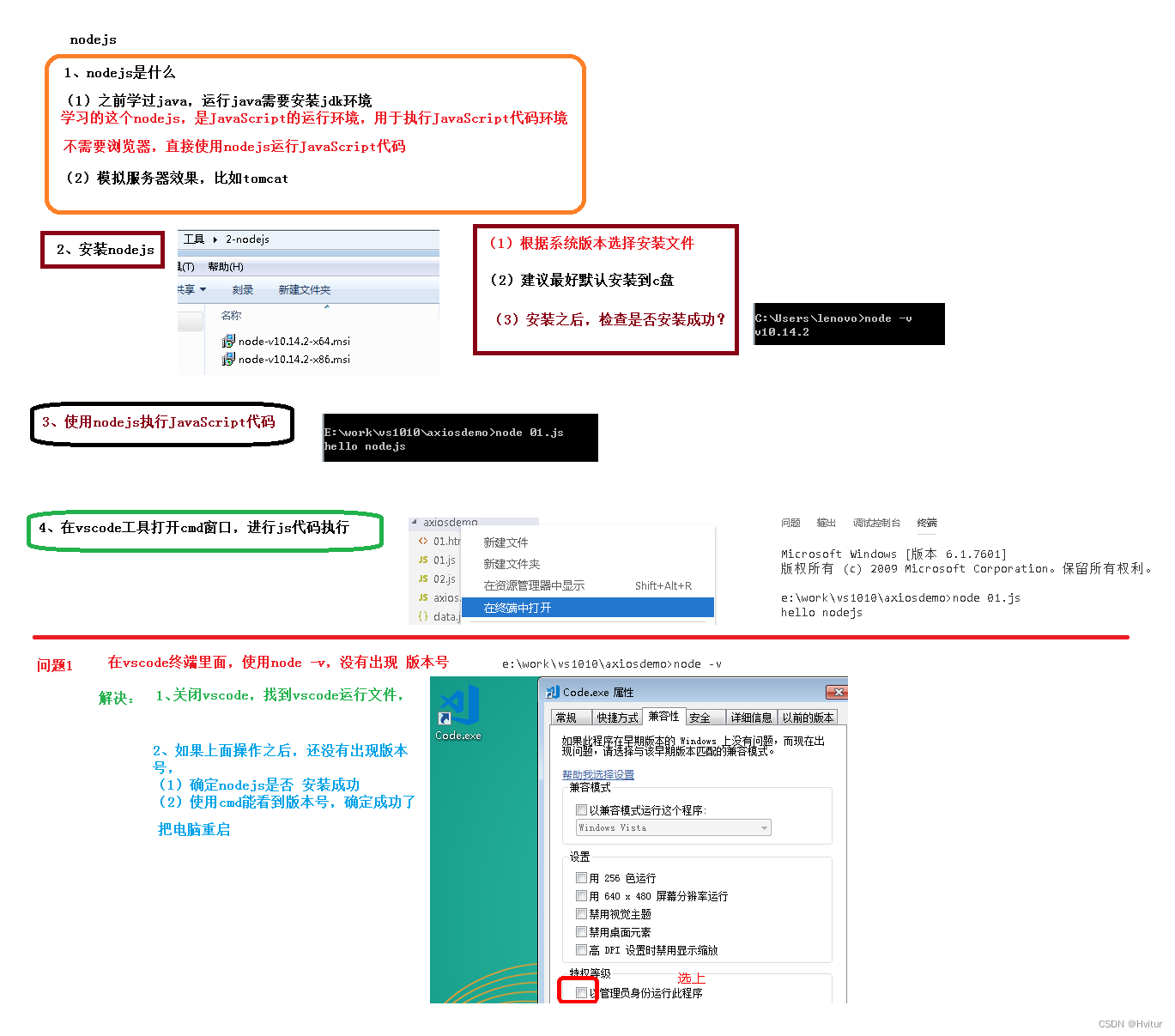
【谷粒学院】vue、axios、element-ui、node.js(44~58)
44.前端技术-vue入门 🧨Vue.js 是什么 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。 Vue 的核心库只关注视图层,不仅易于上手,还便于与第三方库或既有项目整合。另一方面,当与现代化的工具…...

【一些回忆】2022.02.26-2023.02.26 一个普通男孩的365天
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:一些回忆 为什么选择在这个时间节点回忆一下呢? 一是因为今天距离2023高考仅剩1…...
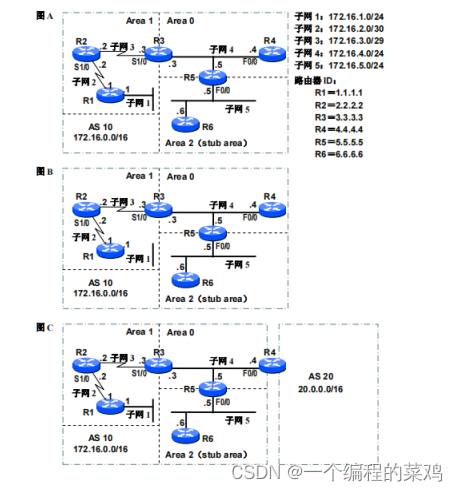
OSPF的多区域特性 (电子科技大学TCP/IP实验三)
一.实验目的 1、掌握OSPF 协议中区域的类型、特征和作用 2、掌握OSPF 路由器的类型、特征和作用 3、掌握OSPF LSA 分组的类型、特征和作用 4、理解OSPF 区域类型、路由器类型和OSPF LSA 分组类型间的相互关系 二.预备知识 1、静态路由选择和动态路…...
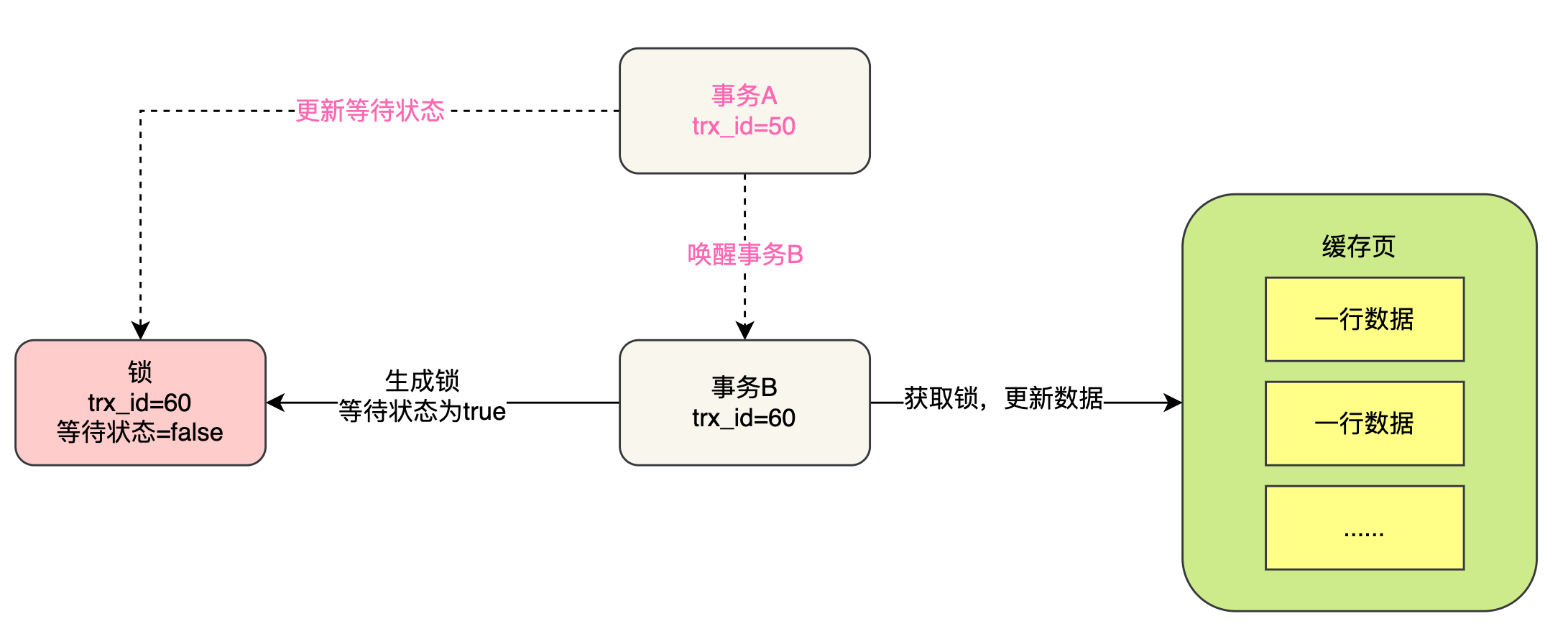
(四十四)多个事务更新同一行数据时,是如何加锁避免脏写的?
之前我们已经用很多篇幅给大家讲解了多个事务并发运行的时候,如果同时要读写一批数据,此时读和写时间的关系是如何协调的,毕竟要是你不协调好的话,可能就会有脏读、不可重复读、幻读等一系列的问题。 简单来说,脏读、…...

【数据库】第十二章 数据库管理
第12章 数据库管理 数据库的物理存储 关于内存、外存、磁盘、硬盘、软盘、光盘的区别_Allenzyg的博客-CSDN博客_磁盘和硬盘的区别 数据库记录在磁盘上的存储 定长,变长跨块,非跨快 文件的组织方方法: 无序记录文件(堆文件heap或pile file…...
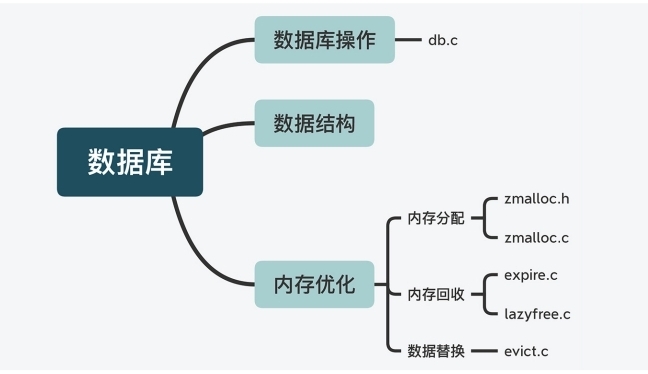
Redis源码---整体架构
目录 前言 Redis目录结构 前言 deps目录 src 目录 tests 目录 utils 目录 重要的配置文件 Redis 功能模块与源码对应 前言 服务器实例 数据库数据类型与操作 高可靠性和高可扩展性 辅助功能 前言 以先面后点的方法推进无特殊说明,都是基于 Redis 5.0.…...
基于springboot+vue的校园招聘系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...
SAP MM学习笔记1-SAP中扩张的概念,如何将一个物料从工厂A扩张到工厂B
MM中在创建物料的时候,最低也得创建如下5个view。 基本数据1 基本数据2 购买管理 会计1 会计2 1,扩张是什么 有时候,你想增加其他的View,比如保管场所 等,你不能用MM02来做编辑,要用MM01来做扩张。这就是扩…...
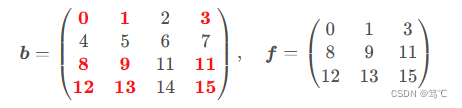
【Python】Numpy数组的切片、索引详解:取数组的特定行列
【Python】Numpy数组的切片、索引详解:取数组的特定行列 文章目录【Python】Numpy数组的切片、索引详解:取数组的特定行列1. 介绍2. 切片索引2.1 切片索引先验知识2.1 一维数组的切片索引2.3 多维数组的切片索引3. 数组索引(副本)…...

2023年全国最新交安安全员精选真题及答案6
百分百题库提供交安安全员考试试题、交安安全员考试预测题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 51.安全生产资金保障制度建立后关键在于落实,各施工企业在落实安全生…...
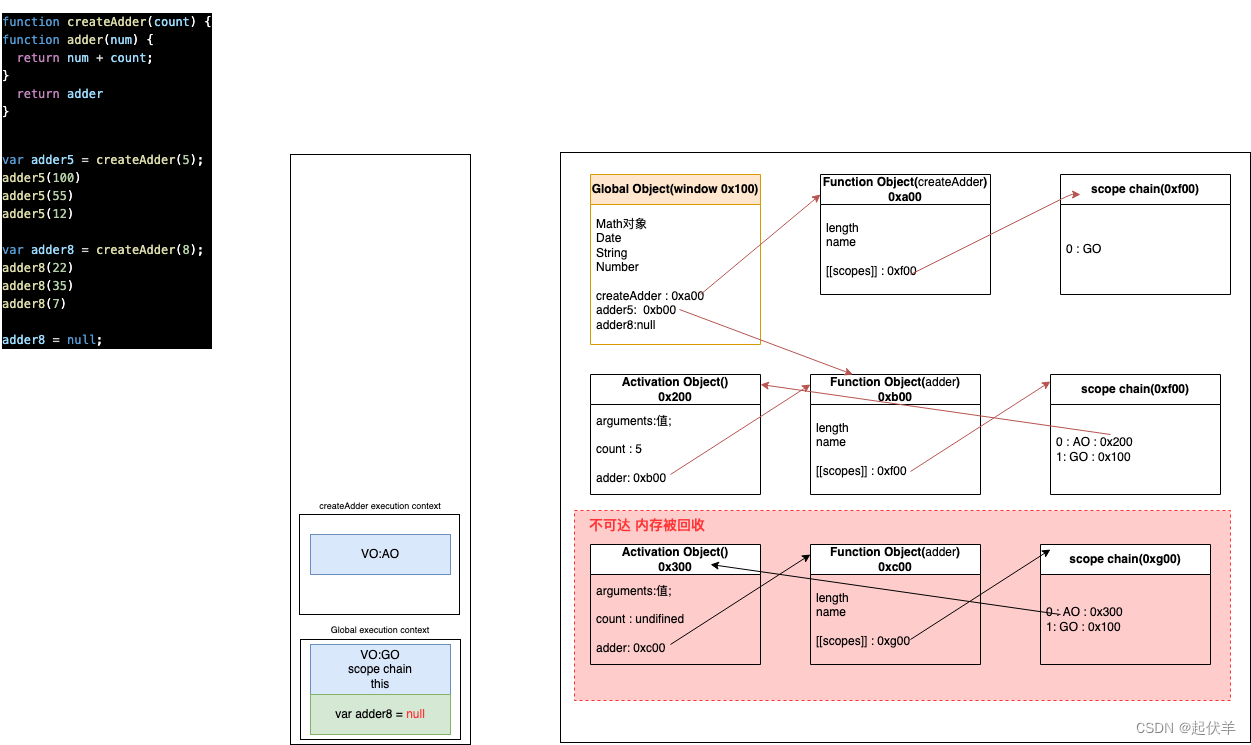
JavaScript 闭包【自留】
闭包的概念理解 闭包的定义 ✅ 这里先来看一下闭包的定义,分成两个:在计算机科学中和在JavaScript中。 ✅ 在计算机科学中对闭包的定义(维基百科): 闭包(英语:Closure),又称词法闭包(Lexical Closure)或函数闭包(function closures);是在支持头等函数…...
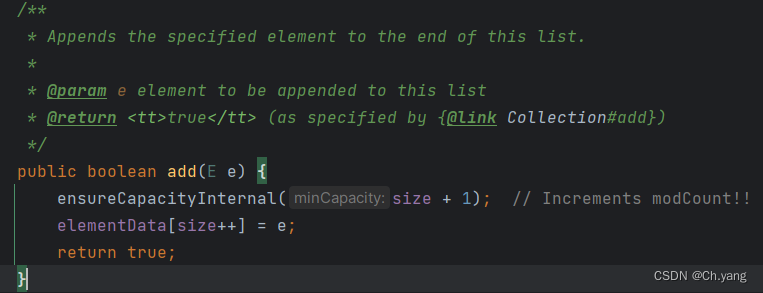
【MySQL】什么是意向锁 IS IX 及值得学习的思想
文章目录前言行锁和表锁使用意向锁意向锁的算法意向锁的思想JDK 中相似的思想前言 之前看 MySQL 都刻意忽略掉了 IS 和 IX 锁,今天看 《MySQL 是怎样运行的》,把意向锁讲的很通透,本篇博文提炼一下思想。 I: Intention Lock(意向…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
