【计算机视觉】3D视觉
文章目录
- 一、基本问题
- 二、三个坐标系
- 三、相机标定
- 四、立体视觉
我的《计算机视觉》系列参考UC Berkeley的CS180课程,PPT可以在课程主页看到。
一、基本问题
我们的最终目标是根据一系列图像构建出整个3D世界。显然,仅凭一张图像是不够的,因为不同大小的事物放在不同的距离拍出来的图像可能是一模一样的。因此,我们需要至少两张图片来理解深度。人眼就是根据双眼所见的细微差别经过大脑处理后感知深度的。
在多视角几何中,我们需要考虑下面几个问题:
- 结构:物体的真实3D坐标是多少?
- 对应关系:给定一张图片中的一个点,它在其他图片中对应哪一个点?
- 运动:给定两张或多张图片的对应点,这些图片之间的相对相机参数(平移、旋转)是多少?
“对应关系”和“运动”是先有鸡还是先有蛋的关系,知道一个就可以推出另一个。
二、三个坐标系
我们需要考虑三个坐标系:
- 世界坐标系;
- 相机坐标系;
- 图像坐标系。
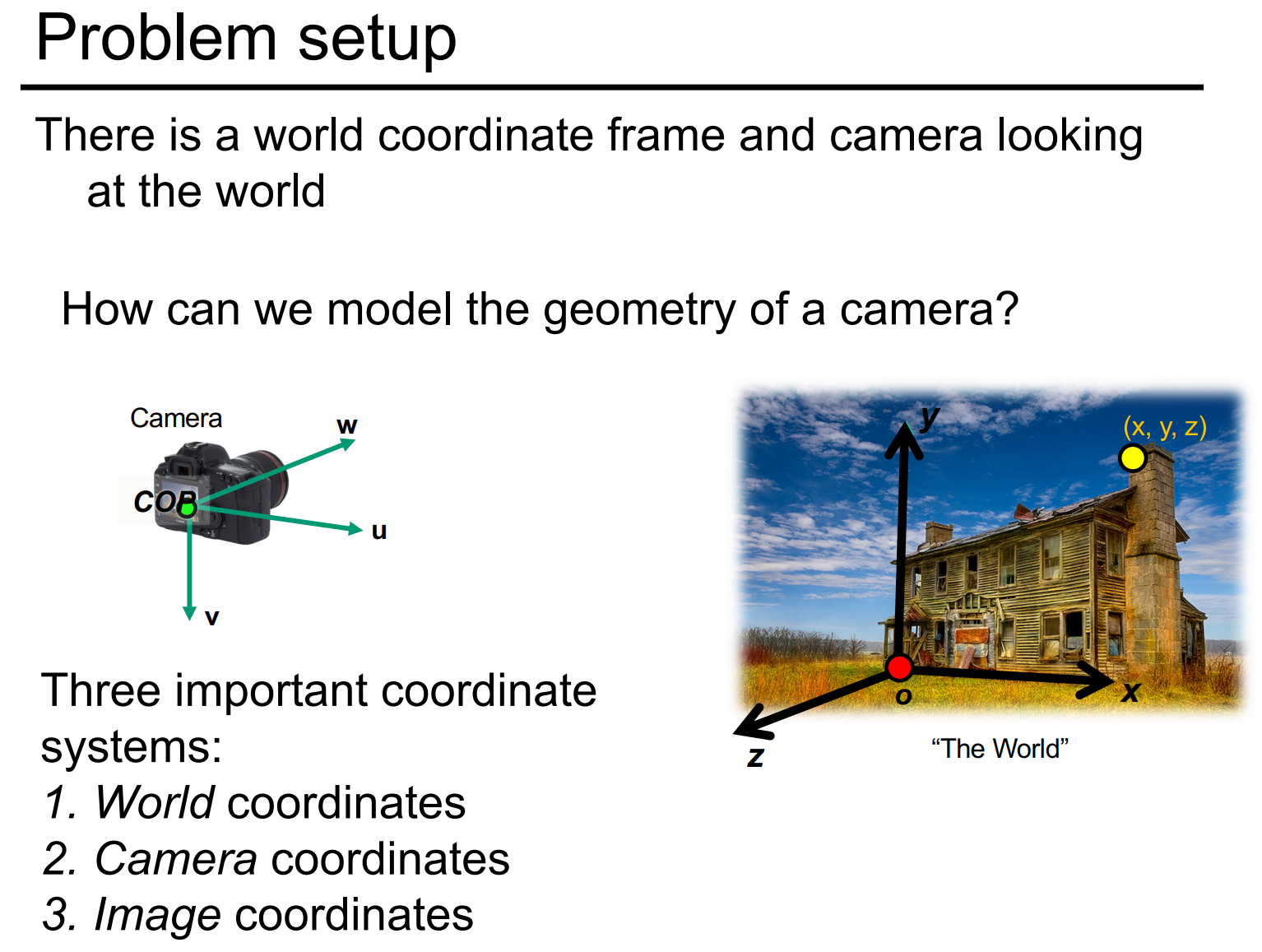
他们之间的转换关系如下图所示。
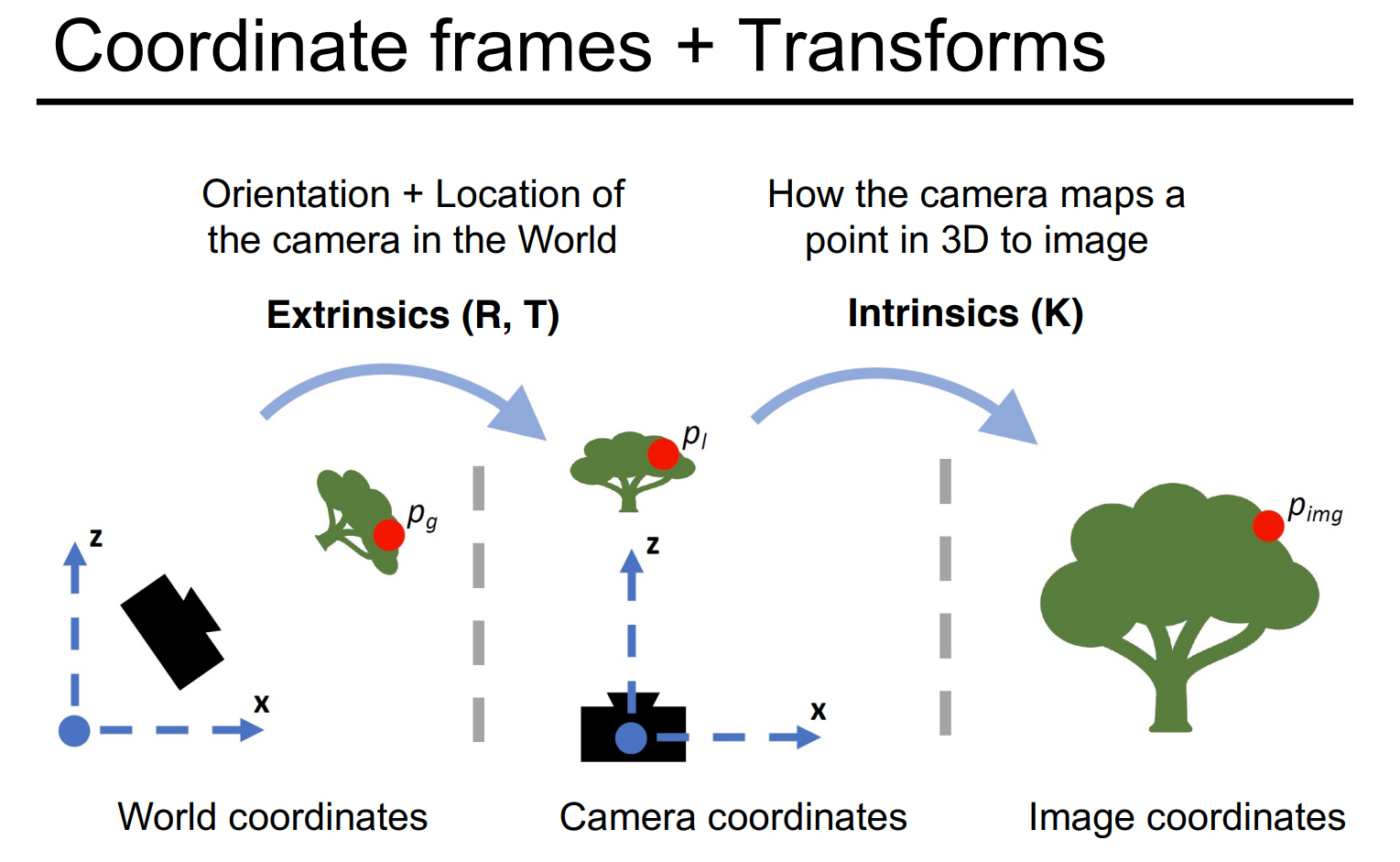
下面我们用数学语言描述这些转换关系。
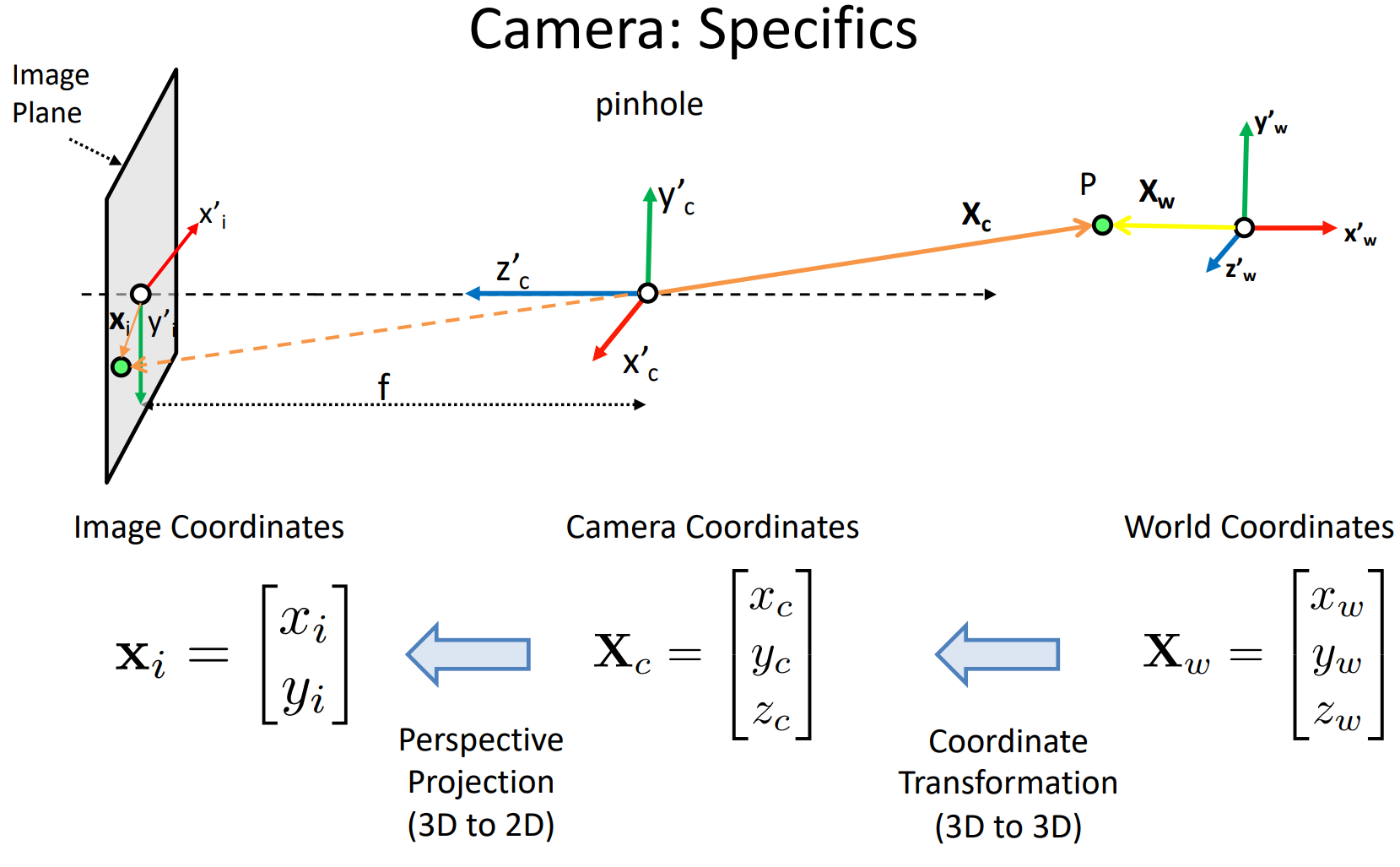
我们有世界坐标 X w = [ x w y w z w ] \boldsymbol{X}_w=\begin{bmatrix}x_w\\y_w\\z_w\\\end{bmatrix} Xw= xwywzw ,相机坐标 X c = [ x c y c z c ] \boldsymbol{X}_c=\begin{bmatrix}x_c\\y_c\\z_c\\\end{bmatrix} Xc= xcyczc (原点在光圈处),以及图像坐标 x i = [ x i y i ] \boldsymbol{x}_i=\begin{bmatrix}x_i\\y_i\end{bmatrix} xi=[xiyi]。从 X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换是3D到3D的坐标变换,从 X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi的转换是3D到2D的投影。
X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换
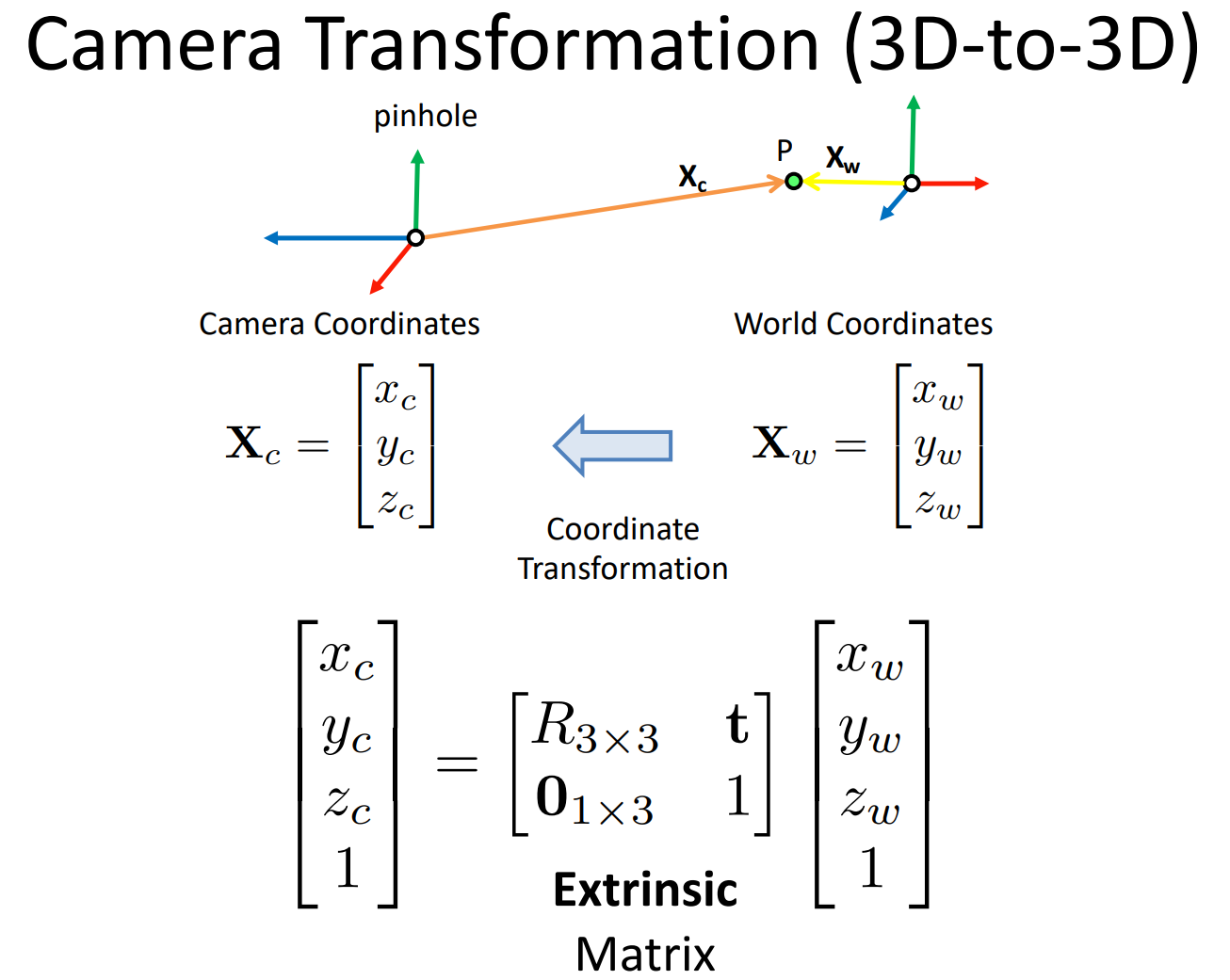
X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换是3D坐标到3D坐标的平移+旋转。一旦涉及平移,就必须使用齐次坐标(homogeneous coordinates)了——需要加一维。平移矩阵是一个 3 × 3 3\times 3 3×3的正交矩阵,向量 t \boldsymbol{t} t是一个3维的平移向量。图中的Extrinsic Matrix是两个操作的结合,它被称为相机的外参。外参共有6个自由度:3个平移自由度+3个旋转自由度(围绕各轴分别旋转)。
记Extrinsic Matrix为 T w 2 c T_{w2c} Tw2c。已知 X w \boldsymbol{X}_w Xw,可以通过 X c = T w 2 c X w \boldsymbol{X}_c=T_{w2c}\boldsymbol{X}_w Xc=Tw2cXw即 [ x c w c z c ] = R [ x w y w z w ] + t \begin{bmatrix}x_c\\w_c\\z_c\end{bmatrix}=R\begin{bmatrix}x_w\\y_w\\z_w\end{bmatrix}+\boldsymbol{t} xcwczc =R xwywzw +t来计算 X c \boldsymbol{X}_c Xc。已知 X c \boldsymbol{X}_c Xc,也可以通过 X w = T w 2 c − 1 X c \boldsymbol{X}_w=T_{w2c}^{-1}\boldsymbol{X}_c Xw=Tw2c−1Xc即 [ x w y w z w ] = R − 1 ( [ x c w c z c ] − t ) \begin{bmatrix}x_w\\y_w\\z_w\end{bmatrix}=R^{-1}\left(\begin{bmatrix}x_c\\w_c\\z_c\end{bmatrix}-\boldsymbol{t}\right) xwywzw =R−1 xcwczc −t 来计算 X c \boldsymbol{X}_c Xc。
X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi的转换
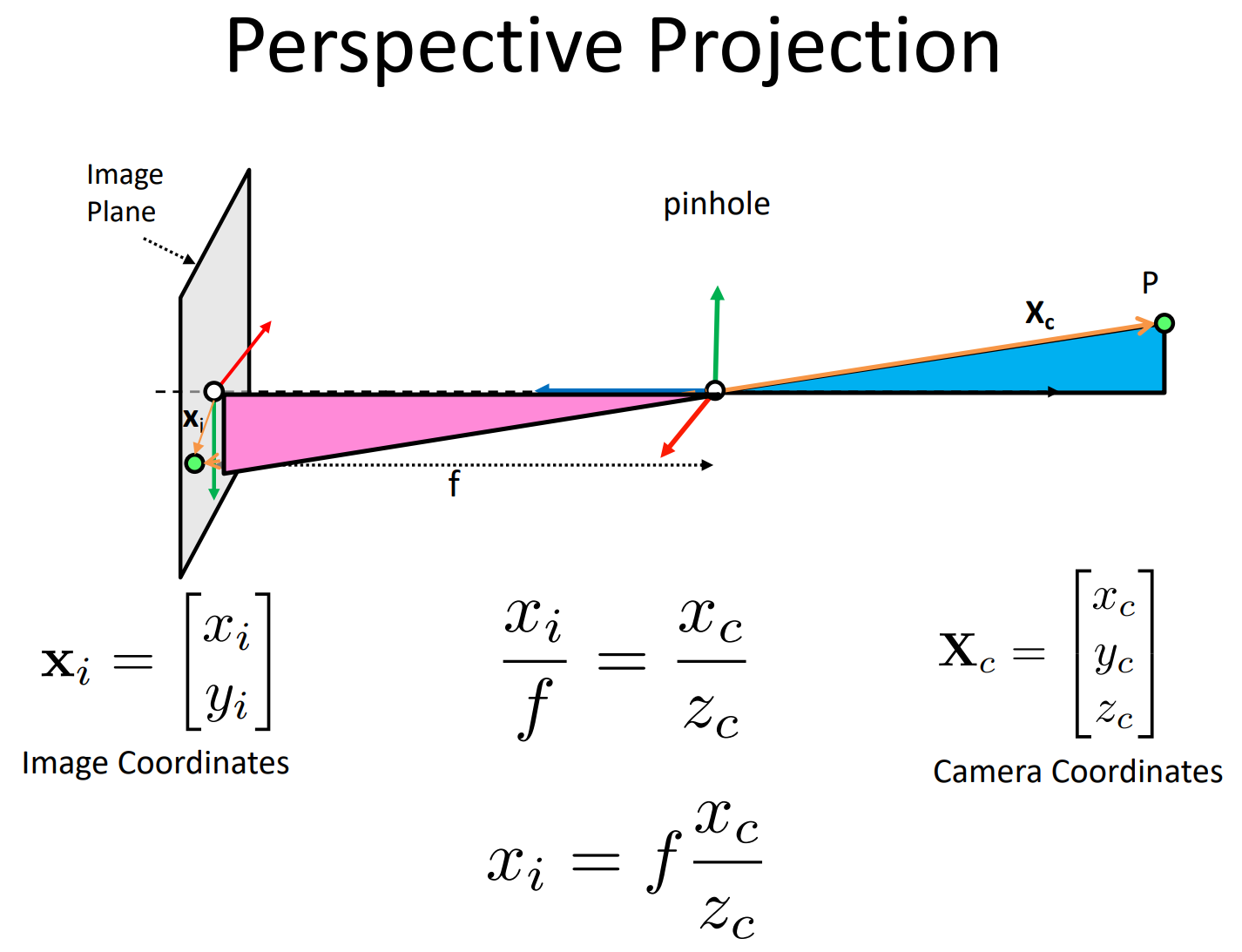
这里的情况稍复杂一些,不仅涉及相机坐标到像平面坐标的投影,还涉及到像平面坐标和最终图像坐标的对应关系。
对于相机坐标到像平面坐标的投影,我们在上一篇文章讲针孔相机的时候已经推过一个式子,这里我们就不必考虑负号了,直接写出 x i = f x c z c y i = f y c z c x_i=f\cfrac{x_c}{z_c}\\ y_i=f\cfrac{y_c}{z_c} xi=fzcxcyi=fzcyc这里假设相机坐标系的 z z z轴和像平面垂直。
此外还有像平面到图像传感器(即图像本身)的对应关系。假设像平面的度量单位是毫米,图像的度量单位是像素,那么就存在这两种单位之间的转化关系;有时水平和竖直方向上像素密度还不一样(横纵比不是1:1),所以需要两个值 m x , m y m_x,m_y mx,my来描述这种密度。像平面的原点往往对应图像的中心,即 ( 0 , 0 ) (0,0) (0,0)不一定对应 ( 0 , 0 ) (0,0) (0,0),所以还需要有一个平移 ( o x , o y ) (o_x,o_y) (ox,oy)。设图像的坐标(单位:像素)为 [ u i v i ] \begin{bmatrix}u_i\\v_i\end{bmatrix} [uivi],则 u i = m x x i + o x = f x x c z c + o x v i = m y y i + o y = f y y c z c + o y u_i=m_x x_i+o_x=f_x \frac{x_c}{z_c}+o_x\\ v_i=m_y y_i+o_y=f_y \frac{y_c}{z_c}+o_y ui=mxxi+ox=fxzcxc+oxvi=myyi+oy=fyzcyc+oy其中 f x = m x f f_x=m_x f fx=mxf, f y = m y f f_y=m_y f fy=myf。我们想要把这个关系表示成矩阵乘法,但是矩阵乘法无法描述除法,所以又要用到齐次坐标。我们知道,齐次坐标 ( x , y , w ) T (x,y,w)^T (x,y,w)T等价于二维坐标 ( x w , y w ) T \left(\cfrac xw, \cfrac yw\right)^T (wx,wy)T,所以我们可以用齐次坐标解决除法的问题。设 ( u i , v i ) T ≡ ( u ~ i , v ~ i , w ~ i ) T (u_i,v_i)^T\equiv (\tilde u_i, \tilde v_i, \tilde w_i)^T (ui,vi)T≡(u~i,v~i,w~i)T( ≡ \equiv ≡代表等价关系),我们只需把 w ~ i \tilde w_i w~i设置成 z c z_c zc, u ~ i \tilde u_i u~i设置成 f x x c + o x z c f_x x_c+o_x z_c fxxc+oxzc, v ~ i \tilde v_i v~i设置成 f y y c + o y z c f_y y_c+o_y z_c fyyc+oyzc即可。这样我们就得到了以下矩阵: [ u i v i ] ≡ [ u ~ i v ~ i w ~ i ] = [ f x 0 o x 0 0 f y o y 0 0 0 1 0 ] [ x c y c z c 1 ] \begin{bmatrix}u_i\\v_i\end{bmatrix}\equiv\begin{bmatrix}\tilde u_i\\\tilde v_i\\\tilde w_i\end{bmatrix}=\begin{bmatrix}f_x&0&o_x&0\\0&f_y&o_y&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix} [uivi]≡ u~iv~iw~i = fx000fy0oxoy1000 xcyczc1 如果像素不是正方形而是平行四边形,还得加一个倾斜变换(skew) s s s: K = [ f x s o x 0 0 f y o y 0 0 0 1 0 ] K=\begin{bmatrix}f_x&s&o_x&0\\0&f_y&o_y&0\\0&0&1&0\end{bmatrix} K= fx00sfy0oxoy1000 这里的 K K K就是Intrinsic Matrix,他被称为相机的内参。这样,内参 K K K就有5个自由度: f x , f y , o x , o y , s f_x,f_y,o_x,o_y,s fx,fy,ox,oy,s。
投影矩阵
把各种变换汇总在一起,就形成了投影矩阵(projection matrix)。 [ u i v i ] ≡ [ u ~ i v ~ i w ~ i ] = [ f x 0 o x 0 0 f y o y 0 0 0 1 0 ] [ R 3 × 3 t 3 × 1 0 1 × 3 1 ] ⏟ 3 × 4 投影矩阵 [ x w y w z w 1 ] \begin{bmatrix}u_i\\v_i\end{bmatrix}\equiv\begin{bmatrix}\tilde u_i\\\tilde v_i\\\tilde w_i\end{bmatrix}=\underset{3\times 4\text{投影矩阵}}{\underbrace{\begin{bmatrix}f_x&0&o_x&0\\0&f_y&o_y&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}R_{3\times 3}&\boldsymbol{t}_{3\times 1}\\\boldsymbol{0}_{1\times 3}&1\end{bmatrix}}}\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix} [uivi]≡ u~iv~iw~i =3×4投影矩阵 fx000fy0oxoy1000 [R3×301×3t3×11] xwywzw1 投影矩阵共有5+6=11个自由度。
尺度模糊问题
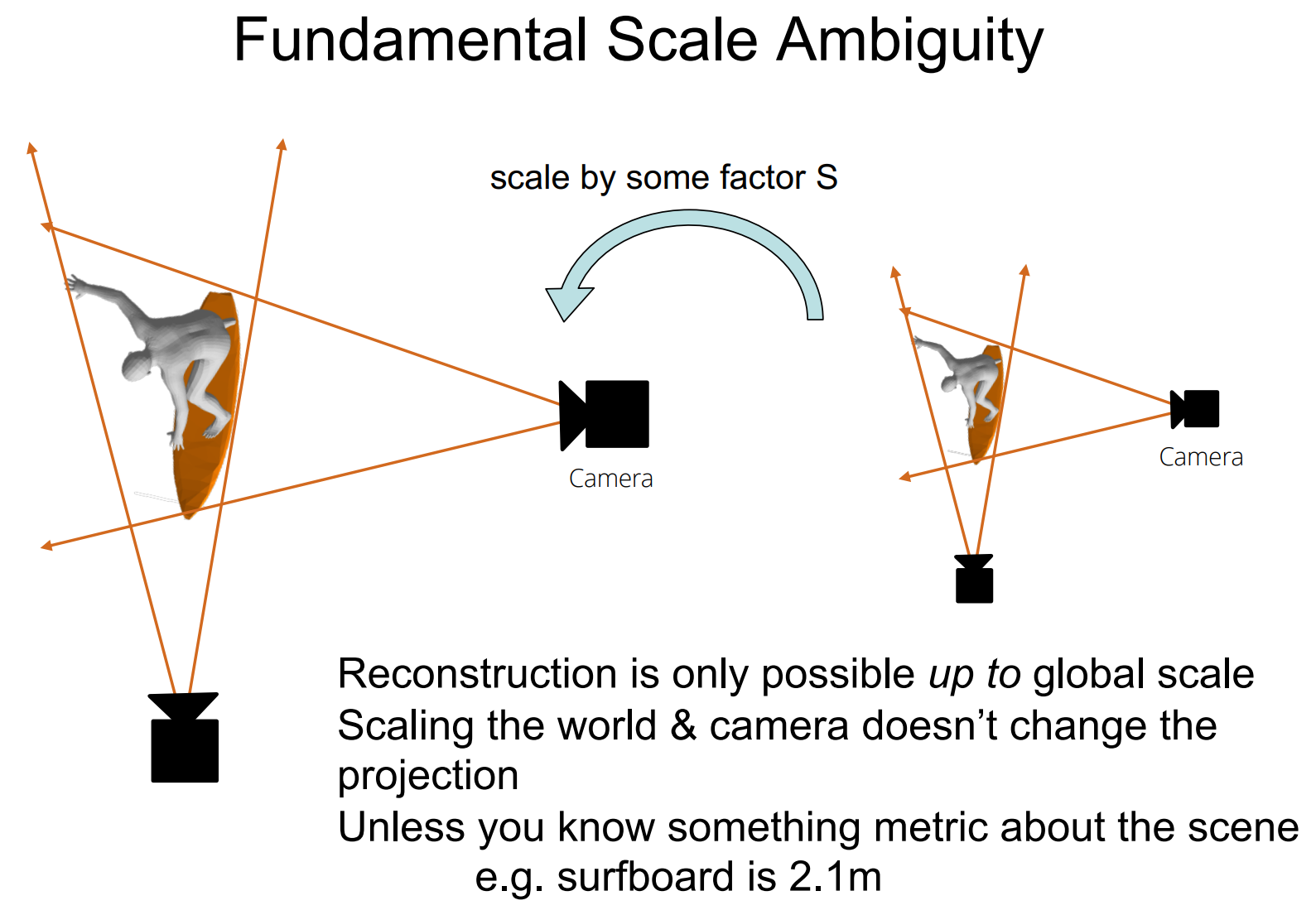
还有一个问题:如果我们把整个世界(包括相机)都放大很多倍,那么拍出来的照片仍然是一模一样的。想要从照片重建世界并且要有精确的尺度,就必须知道世界中某个物体的大小(例如图中的冲浪板是2.1m)。这也就解释了为什么投影矩阵有12个元素但是只有11个自由度。
三、相机标定
那我们如何求得相机的内外参呢?这时候就需要用到相机标定(camera calibration)。基本思路是知道世界中一些物体的3D坐标以及它们在图片上的坐标,通过线性回归(最小二乘法)拟合出投影矩阵。

虽然是拟合矩阵,但也可以转化为一般的多元线性回归问题:
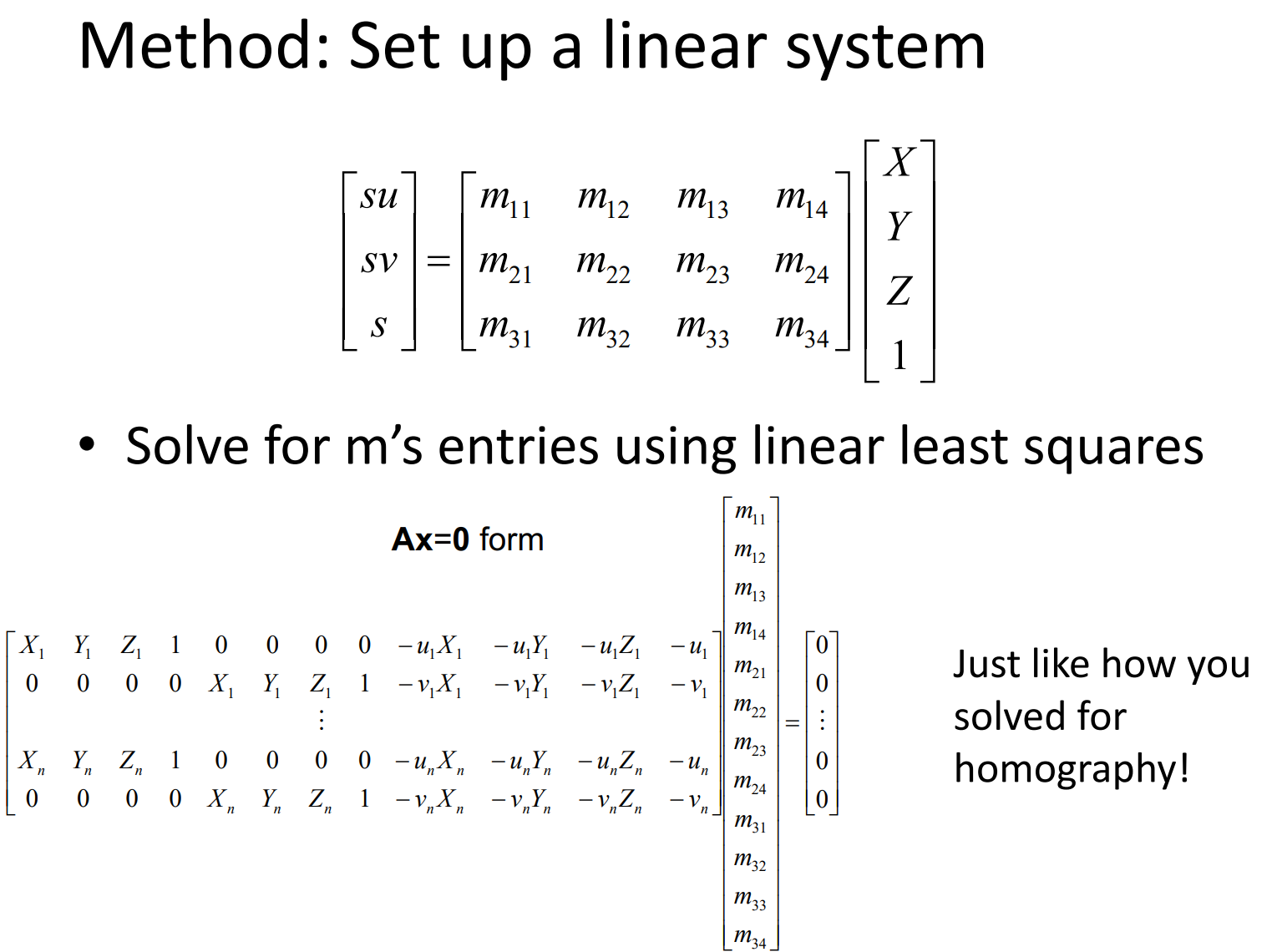
用最小二乘法就可以求出投影矩阵了。知道了投影矩阵,能不能分别求出内外参呢?答案是可以的。注意到内参 K K K只有前三列有非零元,所以令前三列为 U U U,将 K K K分块为 K = [ U 3 × 3 ∣ 0 3 × 1 ] K=[U_{3\times 3}|\boldsymbol{0}_{3\times 1}] K=[U3×3∣03×1]。这样再和外参 [ R 3 × 3 t 3 × 1 0 1 × 3 1 ] \begin{bmatrix}R_{3\times 3}&\boldsymbol{t}_{3\times 1}\\\boldsymbol{0}_{1\times 3}&1\end{bmatrix} [R3×301×3t3×11]相乘就得到了 U [ R ∣ t ] + 0 [ 0 ∣ 1 ] = U [ R ∣ t ] U[R|\boldsymbol{t}]+\boldsymbol{0}[\boldsymbol{0}|1]=U[R|\boldsymbol{t}] U[R∣t]+0[0∣1]=U[R∣t]。注意 R R R是一个正交矩阵, U U U是一个上三角矩阵,所以可以对投影矩阵的前三列进行QR分解(用格拉姆-施密特正交化方法就可以完成),从而求得 U U U和 R R R,再对投影矩阵的第四列左乘 U − 1 U^{-1} U−1即可得到 t \boldsymbol{t} t。
四、立体视觉
从 X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi,可以用内参矩阵 K K K乘以 X c \boldsymbol{X}_c Xc算出来。但是反着来呢?知道图像上的点,能不能知道它在相机坐标系对应哪个点呢?不能,因为只知道两个坐标( u i , v i u_i,v_i ui,vi),是不能求出三个坐标的。相机坐标系里一条直线上的所有点都对应像平面上的一个点。
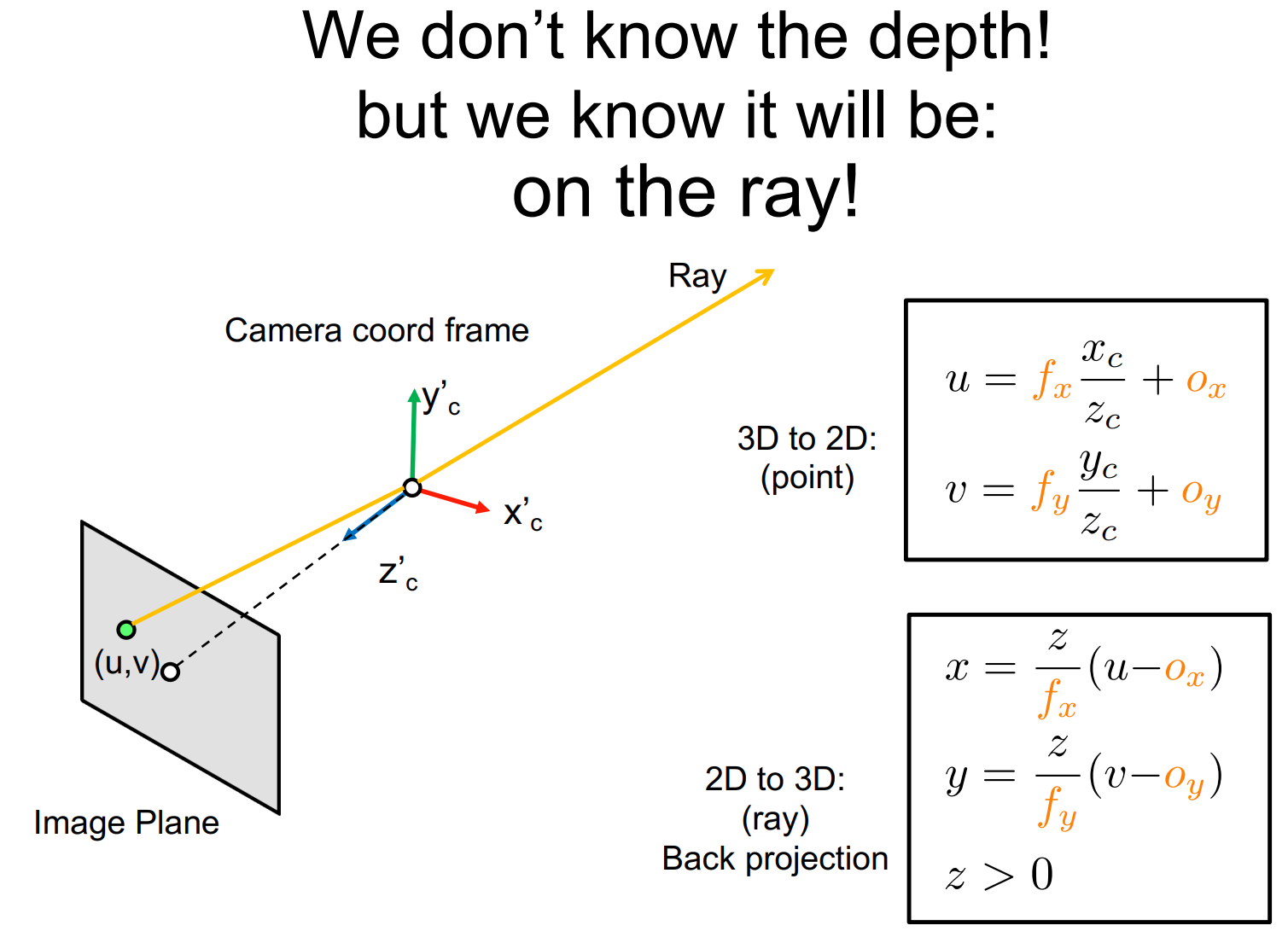
通过图中的公式可以看出,从2D到3D只能得到一条直线,该直线可以表达为关于 z z z的参数方程,但是 z z z可以取任意正数。
那么怎么得到深度 z z z的确切值呢?这时候就需要两张或以上的照片了。人眼的工作方式就是如此。我们先考虑最简单的情况:拍摄两张照片的两个相机光轴是平行的(相当于两个相机的像平面共面)。知道了相机之间的距离,相机的焦距,以及景物的同一个点分别对应在两张照片上的坐标,就可以用相似三角形求解出深度 z z z了:
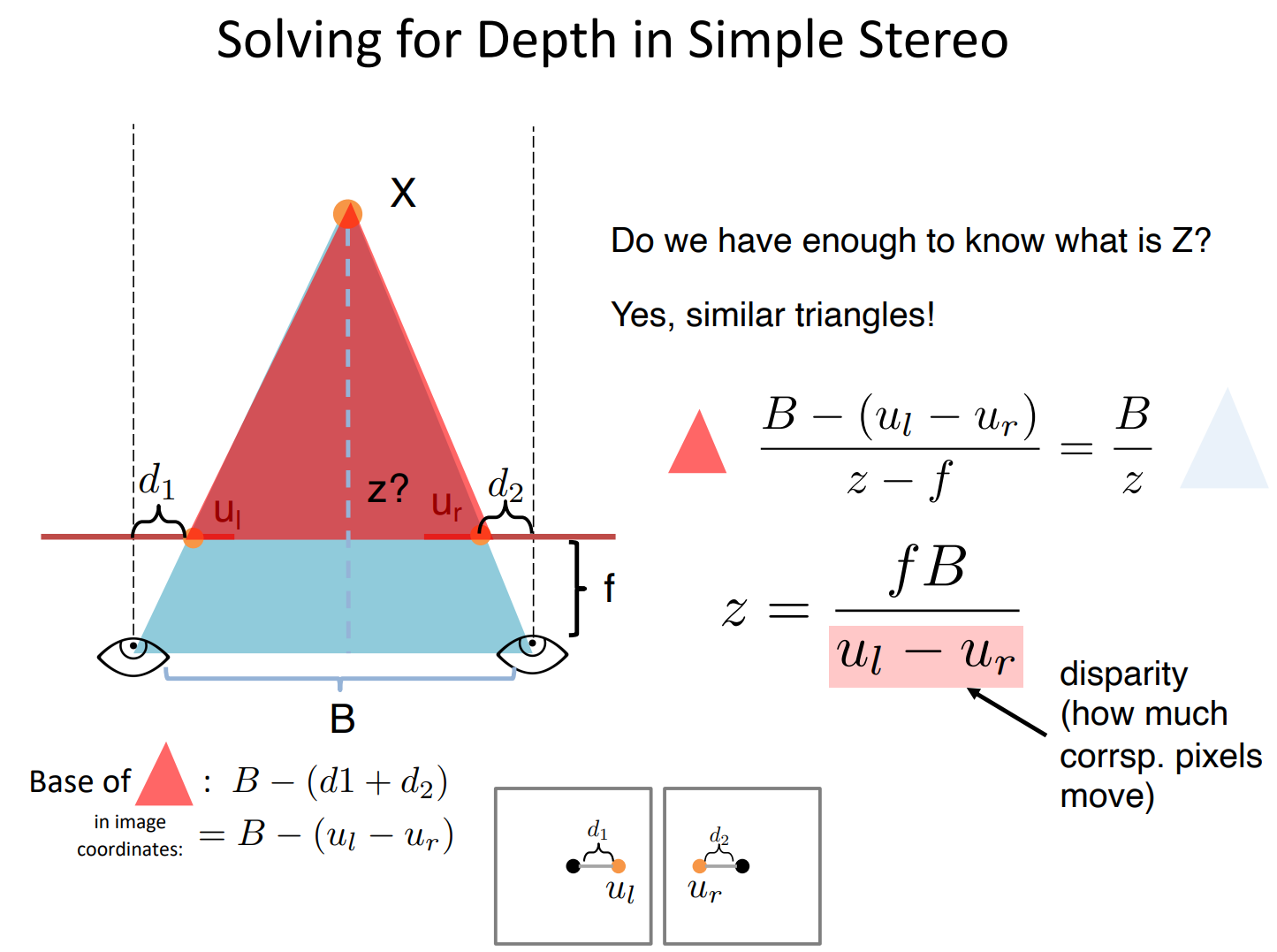
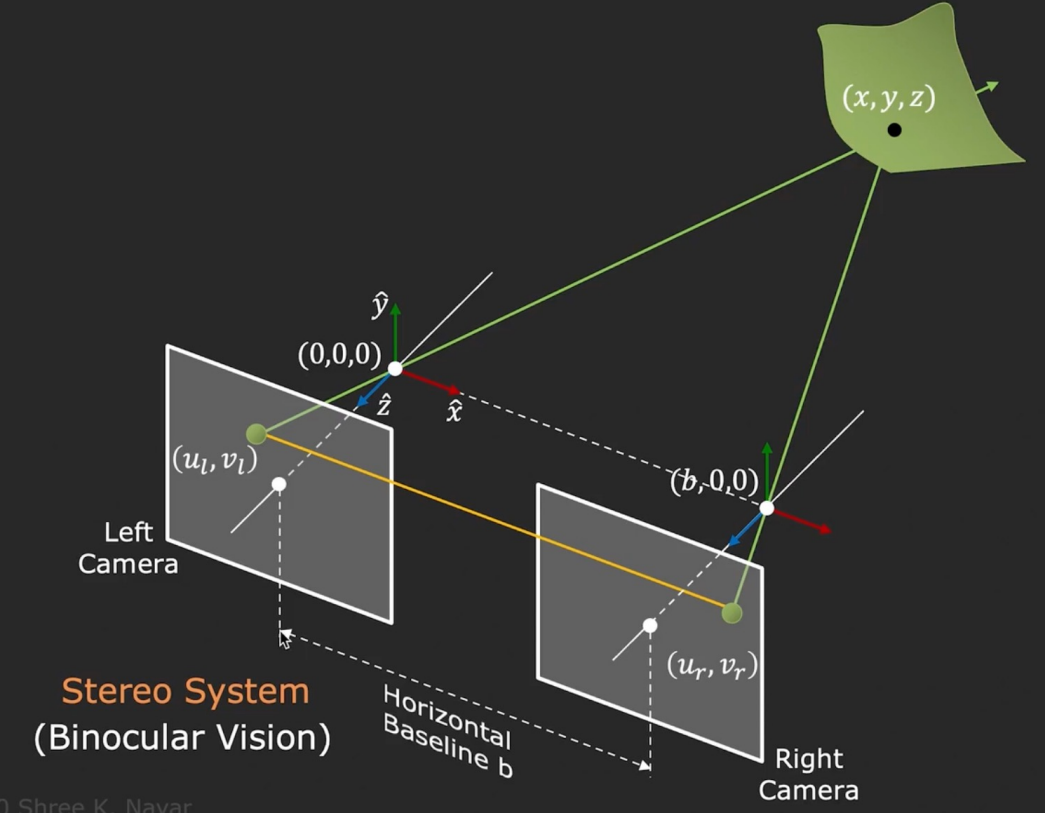
也就是说,相机移动一定距离的情况下景物在照片中移动距离的多少可以为景物的深度提供信息。移动的越多,说明景物离相机越近;反之越远。比如开车时看见路边的树在动,但是太阳却不动。深度与移动的距离成反比。
那么我们怎么自动求出景物在图片中移动的距离呢?也就是说,给定一张图片中的一点,如何求出它在另一张图片中对应哪个点呢?此时我们不知道景物的深度,但景物在第一张图片中的坐标使得我们能够确定景物在某一条直线上。景物在另一个相机(眼睛)的像平面上的坐标是由 该相机的投影中心到景物的射线 与 其像平面 的交点决定的。假设从第一个相机的投影中心到到景物的射线为 l 1 l_1 l1(左图中左边的黄线),第二个相机……的射线为 l 2 l_2 l2(左图中右边的黄线),两个相机/眼睛投影中心之间的直线为 l 3 l_3 l3,则 l 2 l_2 l2与 l 1 l_1 l1和 l 3 l_3 l3都有交点,说明 l 2 l_2 l2在由 l 1 l_1 l1和 l 3 l_3 l3确定的平面 P P P上。不论景物深度如何,从第二个相机到景物的射线(图中的多条蓝线)与第二个相机像平面的交点总是在平面 P P P上,也就是在平面 P P P和像平面的交线上。因此景物在第二张图片中可能出现的位置一定是一条水平的直线。
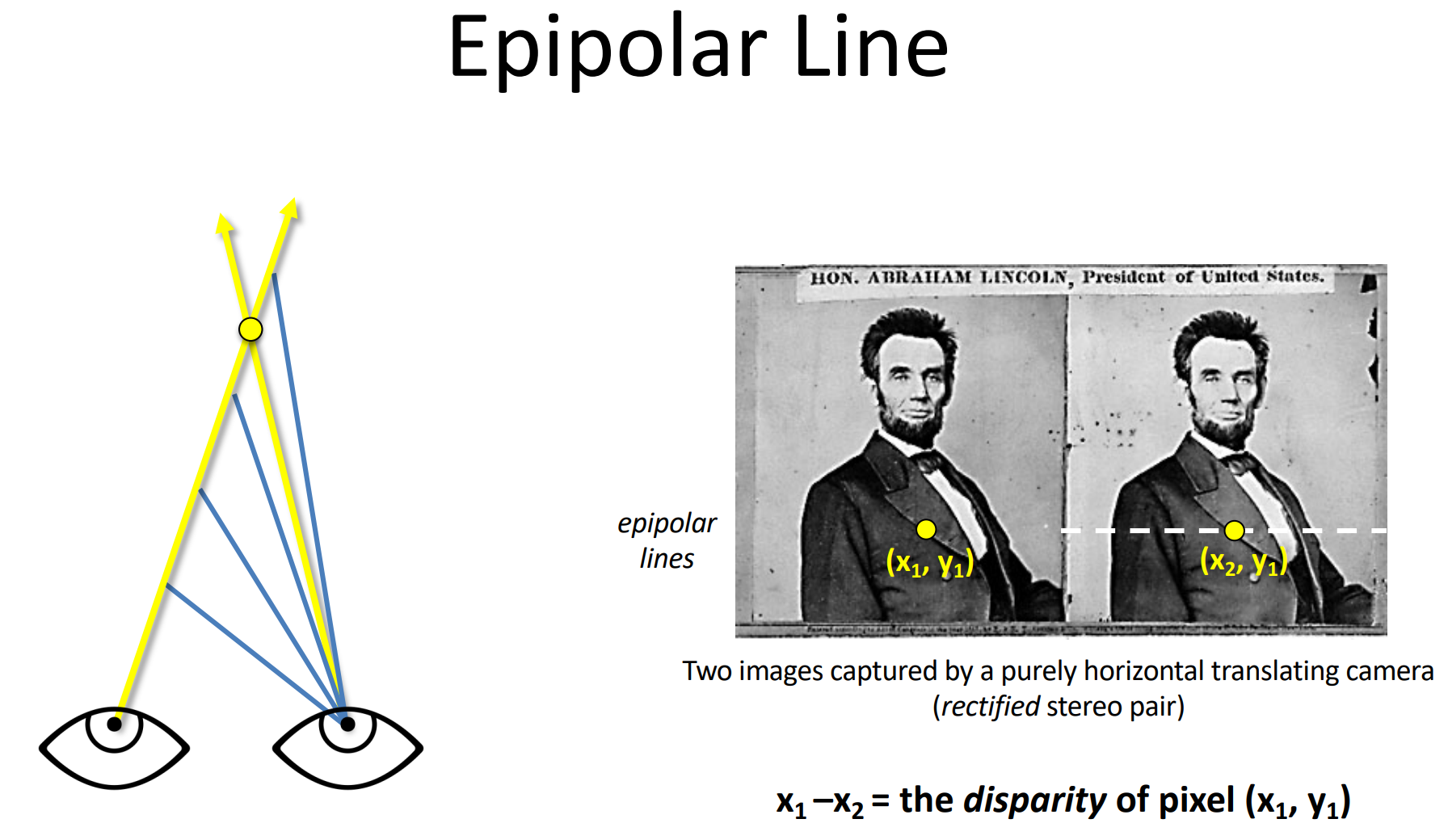
因此我们只需要在第二张图片的那一条水平线上搜索就可以了( y y y与第一张图片一致,只枚举 x x x)。我们可以考虑一个滑动的小窗口,其中心在那条水平线上,与第一张图片景物对应点周围的窗口匹配,匹配度用归一化互相关(Normalized Cross Correlationn, NCC)来计算。我们希望窗口足够大,使得亮度有明显的变化;我们也希望窗口足够小,使得窗口中尽量不包含多个深度的景物。不过,这种方法能够奏效,景物必须有不重复的纹理(白墙、花纹重复的地毯就是大坑);而且近大远小也是一种阻碍,在它的影响下窗口在第二张图片中会有所变形。

相关文章:

【计算机视觉】3D视觉
文章目录 一、基本问题二、三个坐标系 X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换 X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi的转换投影矩阵尺度模糊问题 三、相机标定四、立体视觉 我的《计算机视觉》系列参考UC Berkeley的CS180课程&#x…...

策略路由和路由策略
目录 策略路由 路由策略 策略路由和路由策略 策略路由 Step1:配置ACL,匹配流量 acl number 2010 rule 10 permit source 192.168.10.0 0.0.0.255 acl number 2020 rule 10 permit source 192.168.20.0 0.0.0.255 Step2:流分类traffic classifier jiaoxue //匹配…...
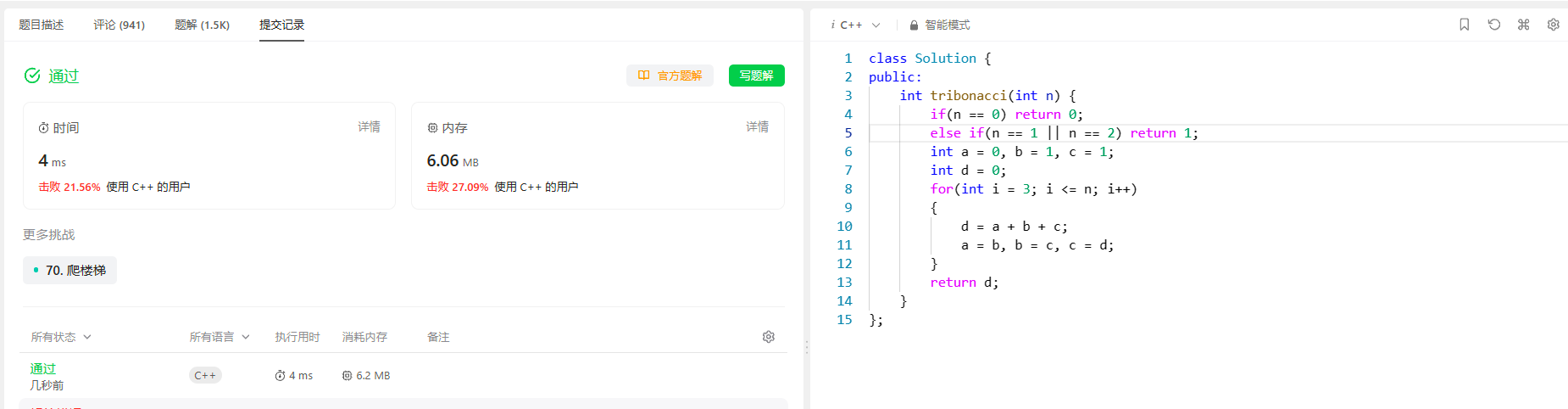
[动态规划] (一) LeetCode 1137.第N个泰波那契数
[动态规划] (一) LeetCode 1137.第N个泰波那契数 文章目录 [动态规划] (一) LeetCode 1137.第N个泰波那契数题目解析解题思路状态表示状态转移方程初始化和填表顺序返回值 代码实现总结空间优化代码实现 总结 1137. 第 N 个泰波那契数 题目解析 解题思路 状态表示 (1) 题目要…...

SystemVerilog语法中,在Class中引用层次化信号
在class中可以像在verilog中一样,直接在class中引用层次化信号。示例如下: 1.DUT模块,文件名为top.v。 module top (input clk ,input rst_n ,//总线信号 input wr_n ,input rd_n ,input cs0_n ,input cs7_n …...
磁盘的结构(磁道,扇区,盘面,柱面,物理地址)
目录 1.磁盘、磁道、扇区的概念1.磁盘2.磁道3.扇区 2.如何在磁盘中读/写数据3.盘面、柱面的概念4.磁盘的物理地址1.根据地址读取一个“块” 5.磁盘的分类1.活动头磁道2.固定头磁盘3.根据盘片是否可更换 1.磁盘、磁道、扇区的概念 1.磁盘 磁盘的表面由一些磁性物质组成…...

uni-app集成uni-simple-router,报错:Uncaught ReferenceError: ROUTES is not defined
参考连接:GitHub - SilurianYang/uni-read-pages: read pages.json file to generate the routes table 作用:配置 vue.config.js 通过 webpack注入全局变量 问题:缺少Webpack 配置环境 方法: 项目根目录下打开终端,…...
几个常用的nosql数据库的操作方式
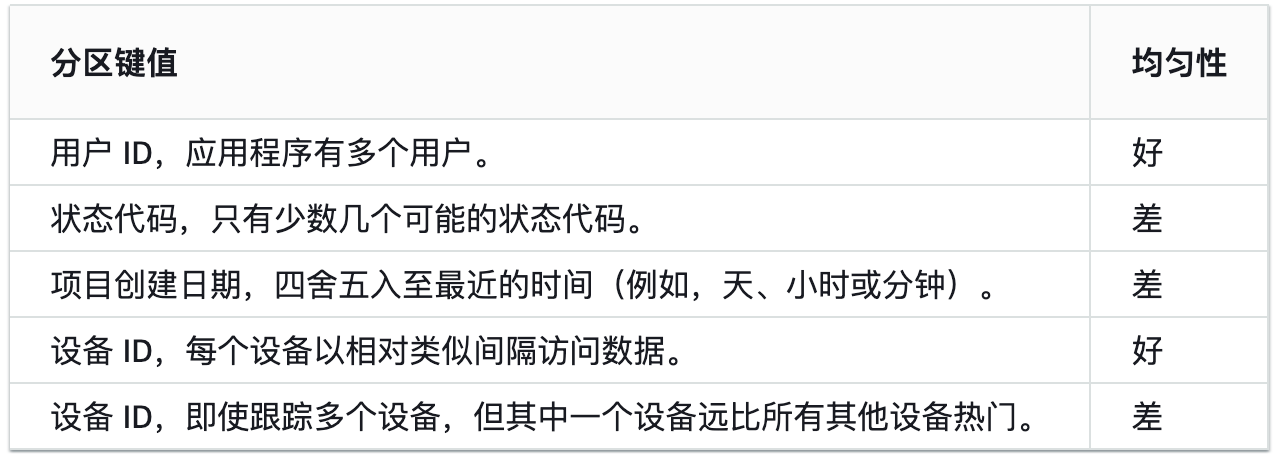
dynamoDB 键 partition key:分区键 定义:分区键是用于分布数据存储的主键,每个项(Item)在表中都必须有一个唯一的分区键值。 特点: 唯一性:每个分区键值在表中必须是唯一的,这是因为…...

如何使用 nvm-windows 这个工具来管理你电脑上的Node.js版本
nvm-windows 是一个用于管理在 Windows 上安装的多个 Node.js 版本的工具。以下是安装和使用 nvm-windows 的步骤: 第1步:下载 nvm-windows 访问 nvm-windows 的 GitHub发布页面.下载最新版本的 nvm-setup.zip 文件。 第2步:安装 nvm-wind…...
公司电脑禁用U盘的方法
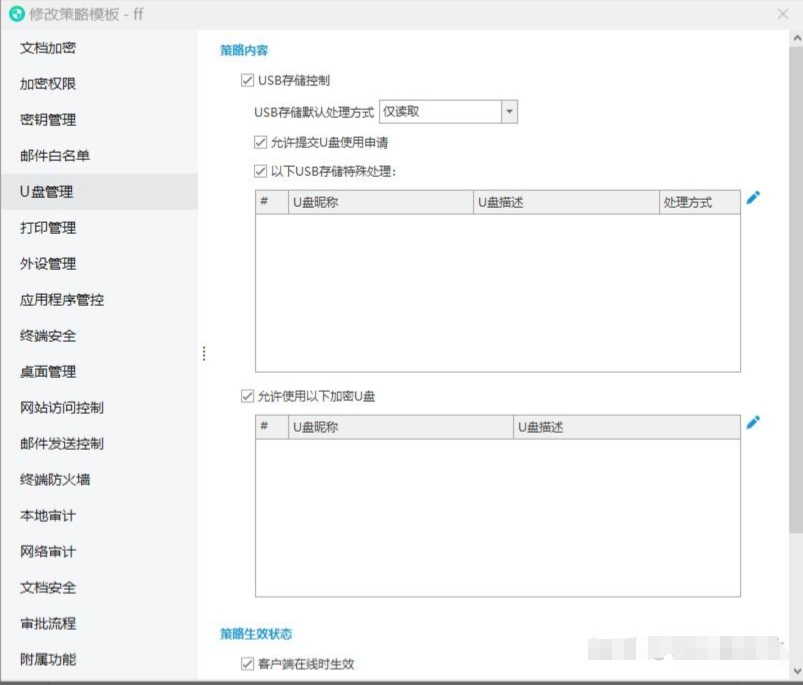
公司电脑禁用U盘的方法 安企神U盘管理系统下载使用 在这个复杂的数据时代,保护公司数据的安全性至关重要。其中,防止未经授权的数据泄露是其中的一个关键环节。U盘作为一种常用的数据传输工具,也成为了潜在的安全风险。因此,公司…...

Elasticsearch 7.X版本常用语法语句
文章目录 监控相关 API查看健康状况查看所有节点查看所有节点详细信息查看主节点查看所有索引查看所有分片 索引管理创建索引查看索引查看索引字段类型修改索引字段删除索引别名给索引添加别名查询某个索引下的别名给索引更换别名给索引解绑别名一个别名绑定多个索引查询index_…...
)
Python分享之数学与随机数 (math包,random包)
我们在Python运算中看到Python最基本的数学运算功能。此外,math包补充了更多的函数。当然,如果想要更加高级的数学功能,可以考虑选择标准库之外的numpy和scipy项目,它们不但支持数组和矩阵运算,还有丰富的数学和物理方…...
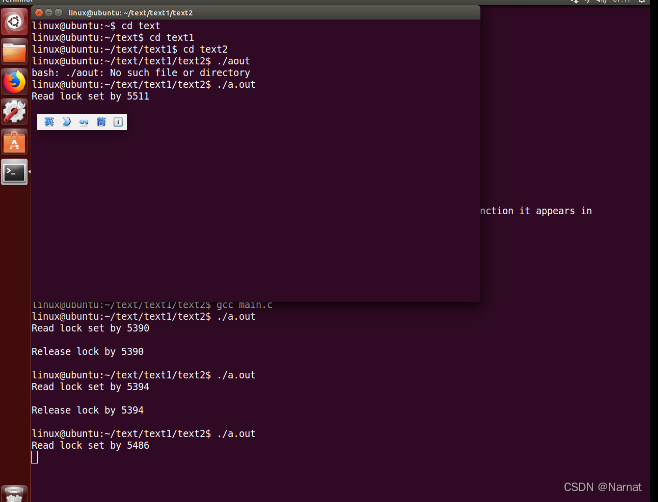
Linux 基本语句_8_C语言_文件控制
为了解决多个进程同时操作一个文件,产生一些情况,通常对文件进行上锁,已解决对共享文件的竞争 对打开文件进行各种操作: int fcentl(int fd, int cmd, .../*arg*/如果cmd与锁操作有关,那么fcentl函数的第三个参数就要…...

博通BCM575系列 RDMA 网卡驱动 bnxt_re 分析(一)
简介 整个BCM系列驱动分成以太网部分(bnxt_en.ko)和RDMA部分(bnxt_re.ko), 两个模块之间通过内核的auxiliary_bus进行管理.我们主要分析下bnxt_re驱动. 代码结构 这个驱动的核心是 qplib_fp.c, 这个文件主要包含了驱动的数据路径, 包括Post Send, Post Recv, Poll CQ流程的实…...
ExcelPatternTool 开箱即用的Excel工具包现已发布!
文章目录 ExcelPatternTool功能特点:快速开始使用说明常规类型高级类型Importable注解Exportable注解IImportOption导入选项IExportOption导出选项单元格样式StyleMapping样式映射使用数据库作为数据源 示例Sample1:不同类型字段导出Sample2:…...
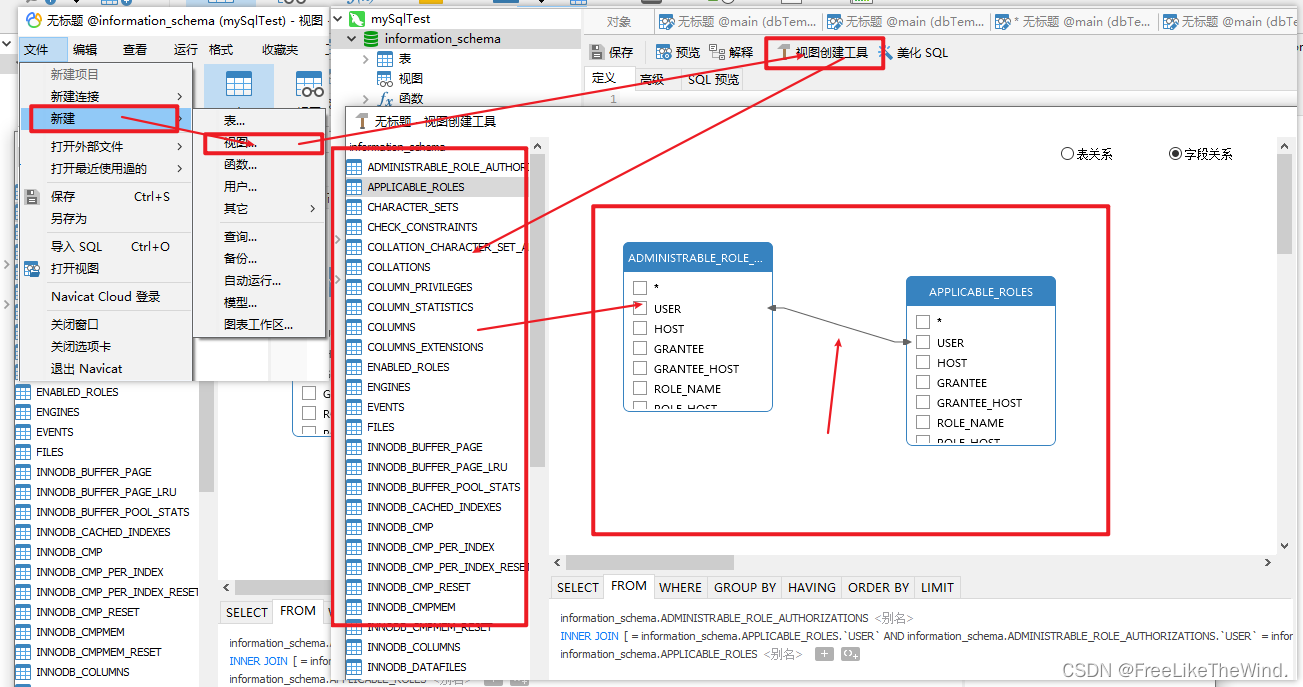
Navicat for MySQL 视图创建使用方法
创建视图步骤: 点击新建;选择视图;点击视图创建工具;可以在左侧拖拽表到工作区;选择表字段进行连线...

计算机视觉的相机选型
#你一般什么时候会用到GPT?# 目前市面上的工业相机大多是基于CCD(ChargeCoupled Device)或CMOS(Complementary Metal Oxide Semiconductor)芯片的相机。一般CCD制造工艺更加复杂,也会更贵一点! 1、CCD工…...
实体店做商城小程序如何
互联网电商深入各个行业,传统线下店商家无论产品销售还是服务业,仅靠以往的经营模式,很难拓展到客户,老客流失严重,同时渠道单一,无法实现外地客户购物及线上客户赋能等。 入驻第三方平台有优势但也有不足…...
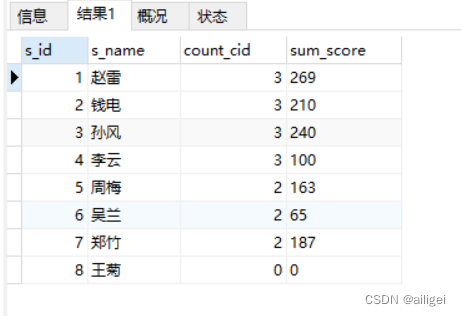
sql-50练习题0-5
sql练习题0-5题 前言数据库表结构介绍学生表课程表成绩表教师表 0-1 查询"01"课程比"02"课程成绩高的学生的信息及课程分数0-2查询"01"课程比"02"课程成绩小的学生的信息及课程分数0-3查询平均成绩大于等于60分的同学的学生编号和学生…...

Flutter框架实现登录注册功能,不连接数据库
要在Flutter框架中实现登录和注册功能,而不连接数据库,可以使用本地存储来存储用户信息。以下是一个简单的示例,演示如何使用本地存储来实现登录和注册功能。 首先,我们需要添加 shared_preferences 插件到 pubspec.yaml 文件中&…...

持续集成部署-k8s-部署利器-Helm
这里写目录标题 1. Helm 是什么?2. 快速安装 Helm2.1 前置条件2.2 Helm 版本与 K8s 版本对应关系2.3 离线安装 Helm3. Helm 常用命令1. Helm 是什么? Helm 是一个用于 Kubernetes 应用程序部署和管理的开源工具。它可以帮助简化 Kubernetes 应用程序的打包、发布、配置和升级…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
