机器学习第一周
一、概述
机器学习大致会被划分为两类:监督学习,无监督学习
1.1 监督学习
监督学习其实就是,给计算机一些输入x和正确的输出y(训练数据集),让他总结x->y的映射关系,从而给他其他的输入x,他能预测出较为准确的y。
接下来举一些监督学习的简单示例:
1.1.1 回归算法
给你训练数据集(x,y),拟合出一条直线或者曲线,能够完美的反应x和y的关系,从而给你其他的数据x,能够通过拟合线计算出y。
1.1.2 分类算法
通过某些特征,将数据进行分类。
1.2 无监督学习
给你一些数据,算法会自动帮你划分数据。(与分类算法的区别:分类算法中,已经对数据x打上标签y,对这些标签进行分类。但是无监督学习,数据没有标签,算法自动对他进行划分,即只有输入x,没有输出y)
1.2.1 聚类算法
获取没有标签的数据,并尝试自动将他们分组到集群中。
1.2.2 降维算法
二、单变量线性回归模型
给出训练集(x,y),拟合出一条直线f(x)=wx+b,能够将测试集xi带入,计算出yi。
2.1 代价函数
w,b被称为模型参数,我们需要定义代价函数,来说明w,b拟合效果的好坏。
假设m表示训练集的大小,y-hat表示计算值,y表示真实值
成本函数:J(w,b)=1/2m(i=1.....m)(y-hati-yi)^2,(用计算值-真实值的平方 的平均值来估计w,b拟合效果的好坏)这里不是除以m而是2m,是为了方便后续的计算,不再除以2也是可以的。他也被称为平方误差成本函数。
在机器学习中,会有不同定义的成本函数,平方误差成本函数是其中之一,且效果好。
我们需要根据成本函数、训练数据,来计算出可以使cost最小化的模型参数w和b。
将w,b,J画成三维图,发现是一个碗的形状。我们将碗用J的等值面切割,会得到等高线图,他表示不同的(w,b)会有相同的J。越靠近等高线图的中心,J会越小。

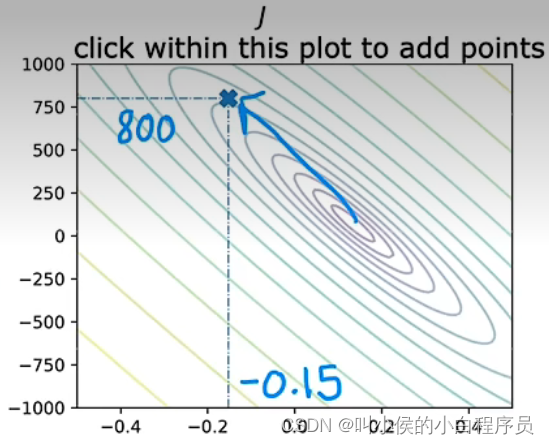
我们需要一个高效的算法,帮助计算最优模型参数。梯度下降法是个好方法。
2.2 梯度下降法
梯度下降法适用于求任何函数的最小值。步骤如下:
- 确定想要最小化的函数J(w,b)
- 设置w,b的初始值(一般初始化为w=0,b=0)
- 每次改变w,b,使J一直变小
- 直到J稳定或接近最小值

梯度下降法的简单理解:如图所示,当站在最高处,环绕360°,选择一个方向,可以使我迈出一小步,却能更快接近谷底,这个方向就是梯度下降最快的方向。到达下一个点后,继续环绕360°,选择一个最快接近谷底的方向。。。。如此反复,就能到达谷底。

当选择不同的初始值,使用梯度下降法可能会到达不同的谷底,这被称为局部最小值。
2.2.1 梯度下降法的实现
执行第三步骤时:给w赋值成 这里的
这里的表示学习率。学习率通常是0-1之间的小正数,他的作用是控制下坡的步幅。
同理需要更新b值。值得注意的是,更新的步骤要合理,如下图所示,左边是正确的,右边是错误的,这是因为,更新b时需要计算J对b的偏导数,此时需要用到w的原始值。

2.2.2 学习率
学习率对实现梯度下降的效率有巨大的影响。若学习率太小,到达最低点需要很多步骤,效率低;若学习率太大,梯度下降法可能会越过最低点,甚至无法收敛。
2.2.3 批量梯度下降
批量梯度下降指的是,在梯度下降的每一步中,我们都查看所有的训练示例,而不仅仅是训练数据的一个子集。
其他版本的梯度下降,在每个更新步骤查看训练数据的较小子集,而不是查看整个训练集。
三、多元线性回归
3.1 多维特征
现在有多个输入x1,x2......xn,一个输出y,怎么实现线性回归呢?
拟合函数(
)=w1x1+w2x2+w3x3+w4x4+b=
+b
在多元线性回归(多变量线性回归)中,应该使用矢量化的方法来简化表达和加快计算速度。
3.2 用于多元线性回归的梯度下降法
如下图,左边是原始版本,右边是矢量化版本的表达方式:

如下图,左边是单元线性回归更新模型参数的公式,右边是多元线性回归的:

3.2.1 特征缩放
在面对多维特征问题的时候,我们要保证这些特征都有具有相近的尺度,这会帮助梯度下降算法更快的收敛。
对于多维特征x1,x2......xn,每个特征的值域不同,有的特别小,有的很大。放到特征散点图中,可以看到,值域大的特征宽泛,值域小的窄瘪。放到等高线图中可以看到,参数小的(特征值大,因此参数会小)等高线窄(因为参数w1对应地特征值大,w1的一点点小改动,可能会对拟合函数f产生较大影响),参数大的(特征值小,因此参数较大)等高线宽,总体呈现出一种压扁的椭圆形状。

由于等高线又高又瘦,梯度下降法会在找到最小值之前来回弹跳很长时间。 因此我们需要做特征缩放,使每个特征的值域在0-1之间。下图是特征缩放前后散点图和等高线图的变化。
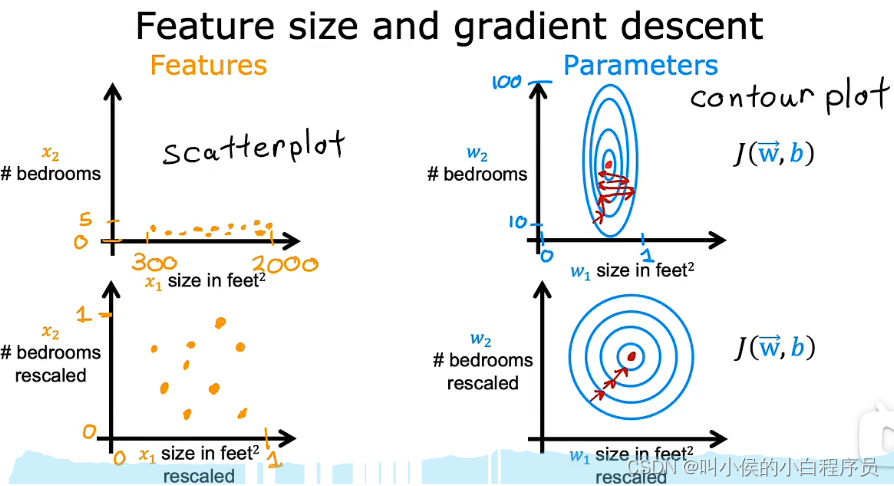
如何实现特征缩放呢?
方法一:每个特征值除以值域的最大值
方法二:均值归一化,每个特征值减去均值,在除以值域的范围(最大值-最小值)
方法三:Z分数归一化,每个特征值减去均值,再除以标准差
我们只要保证每个特征的值域在一个合理的范围就可以,如果某个特征的值域偏大或者偏小,就可以对他进行特征缩放,从而保证梯度下降法可以更快的收敛。
3.2.2 如何判断梯度下降是否收敛
方法一:
绘制学习曲线,横轴表示梯度下降算法的迭代次数,纵轴表示成本函数J的大小,如下图所示:
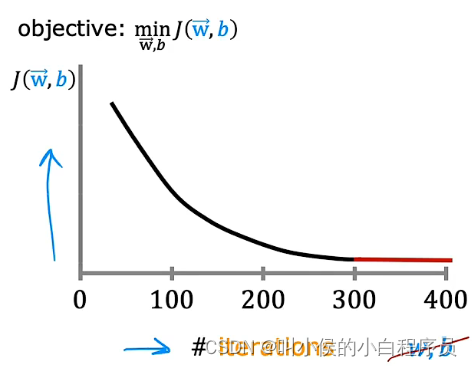
如果梯度下降正常工作,那么成本J每次都应该减少;若J在一次迭代后增加,这意味着选择不当(通常是
太大或者代码存在错误)。在迭代300次以后,成本J基本就稳定不变了,这意味着梯度下降算法收敛了。
方法二:
自动收敛测试,设置一个很小的量,当J在一次迭代后减小的幅度小于
,就将其判定为收敛。
3.2.3 如何设置学习率
如果您绘制多次迭代的成本并注意到成本有时上升有时下降,您应该将其视为梯度下降无法正常工作的明显迹象。说明可能学习率太大,或者代码中有错误。

若学习率太小,J下将会非常缓慢。所以我们应该先选一个非常小的学习率,然后逐步放大,直到不能再放大,就能找到最合适的学习率。
3.3 正规方程
梯度下降是最小化成本函数J以找到w和b的好方法,但还有另一种算法----正规方程,它仅适用于线性回归,不需要迭代梯度下降算法。正规方程法的一些缺点是:首先,与梯度下降不同,这不会泛化到其他学习方法;其次,若特征很多,计算效率低。
不需要要了解这种方法的具体实现细节,我们学会调用库函数就可以了!!!
3.4 特征工程
特征的选择对学习算法的性能具有较大的影响。
比如说估计房子的价格,目前有两个特征:房子的宽度W、长度L。我们可以设计拟合函数为=w1x1+w2x2+b;
我们可以设计第三个特征:房子的占地面积S=W*L,拟合函数变成=w1x1+w2x2+w3x3+b;
我们刚才所做的,创建一个新特征是所谓的特征工程的一个例子,你可以利用你对问题的知识或直觉来设计新特征(通常是通过转换或组合问题的原始特征)来使学习算法做出更准确地预测。
3.5 多项式回归
前面所学的单变量线性回归、多元线性回归,都是拟合为直线。但是假如只有一个特征x,可能呈现的不是直线的模型,这时候就需要用到多项式回归、
、
等。
四、逻辑回归
今天开始我们将学习监督学习的第二大类---分类算法,其中逻辑回归是经典算法之一。只有两种可能输出的分类问题-----二元分类。
介绍逻辑回归之前,先了解一个函数,sigmoid function(logistic function):
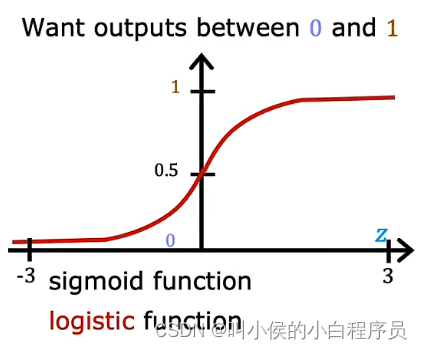
逻辑回归的数学公式:g(z)=
构建逻辑回归算法:
- 确定拟合函数,例如线性回归函数z=wx+b。
- 将拟合函数带入sigmoid 函数g(z)=
从此便构建出来逻辑回归算法=
。他的作用就是,输入特征集,输出0-1之间的数字。
4.1 决策边界
观察逻辑回归公式的曲线,将z输入,输出的数永远都是0-1之间的数据f。我们可以将输出f视为概率。例如f(z)=0.7 ,我们可以认为有0.7的概率预测是1。
当z=0时,f(z)=0.5,约定f0.5 时,输出1,f<0.5 时输出0。因此z=0是决策边界,由于z有不同的表达式,所以z=0边界的形状有各种各样的。
4.2 代价函数
之前讲线性回归时,代价函数是平方误差成本函数,但是这种方法不适用于逻辑回归。因为将代价函数J可视化后,可以看出,在线性回归中J呈现碗状,利用梯度下降算法,可以找到最小值;但是在逻辑回归中,J呈现锯齿状,有好多个局部最小值,所以不适合做逻辑回归的代价函数。

我们需要找到一个新的代价函数,来衡量参数w、b的优劣。如下图所示:若=1,成本函数为-log(f),f取值范围为0-1;因此成本函数呈现碗状,并且当预测值f越接近于1,成本函数J越小。同理
=0。
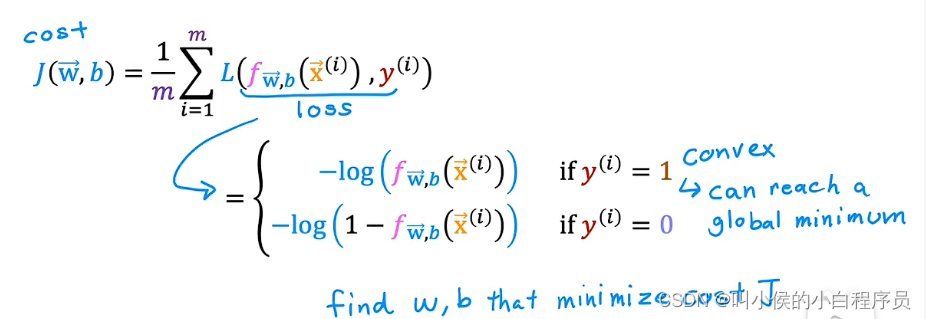
4.2.1 简化逻辑回归代价函数
将以上的函数简化成一个式子表达:

接下来可以推导出成本函数:
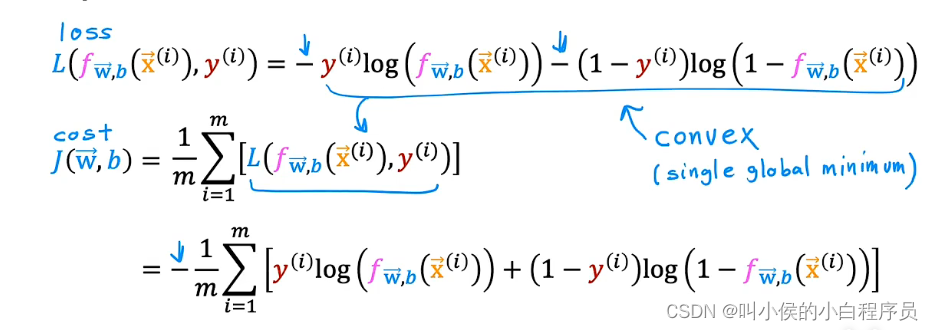
4.3 梯度下降
得到损失函数后,每次迭代更新参数w、b,每次都使J下降,直到J维持不变。

4.4 过拟合问题
使用线性回归预测房屋价格,输入特征是房子的面积,如下图所示:

肉眼可以看出,这不是一个好的模型,他不能很好地拟合训练数据,被称为模型对训练数据欠拟合(或者 算法具有高偏差)。
现在我们换成多项式回归的方法:

这个模型可以很好的拟合训练数据,学习算法能够很好地泛化,这意味着即使在它以前从未见过的全新示例上也能做出良好的预测。
现在使用四阶多项式拟合训练数据:
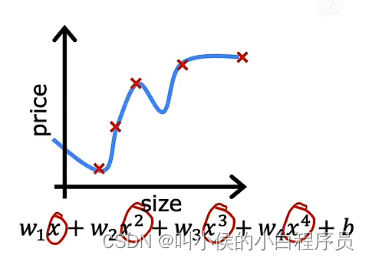
看起来,这条拟合曲线完美的通过了所有的训练示例, 成本函数为0。但是这是一条摇摆不定的曲线,甚至在某些地方,他预测的房屋价格比面积更小的房子的价格都低,这显然不符合常理。我们将这种情况称为过度拟合(或者 算法具有高方差)。
以上的问题同样会出现在分类算法中,下图中x1表示肿瘤大小,x2表示患者年龄,0表示良性肿瘤,+表示恶性肿瘤。下图从左到右分别是欠拟合、完美、过度拟合:

4.4.1 解决过拟合问题
方法一:
使用更多的训练数据集,学习算法将会适应一个波动较小的函数。

方法二:
减少特征,如果特征太多,但是没有足够多的训练数据,也可能会出现过度拟合的状况。选择最合适的一组特征来使用,也称为特征选择。
方法三,正则化:
正则化相对于方法二更加温和,他没有直接删除某些特征或多项式,而是将其参数w设置成一个非常小的数,以此来减少相应特征的影响力。从而曲线能很好的拟合训练数据。正则化的作用是,它可以让你保留所有特征,它们只是防止特征产生过大的影响(这有时会导致过度拟合)。

正则化的方法,只适用于正则化参数w,对于参数b基本没有什么作用。(加入特征很多,我们一时间无法准确判断哪些特征值得保留、哪些需要正则化)正则化的典型实现方式是惩罚所有的特征,或者更准确地说,惩罚所有的W参数,并且这通常会导致拟合更平滑、更简单、也不太容易过度拟合。
4.4.2 正则化
如下图所示:成本函数的左边是为了拟合训练数据,右边是正则化系数。分析的作用:当
等于0时,相当于对任何系数都没有正则化,曲线如下图蓝线所示(数据过度拟合);当
等于无穷大时,
的系数无穷大,那么求成本函数J最小值时,w一定会无限趋近于0,则f=b,曲线如下图紫色线所示,趋近于一条直线(欠拟合)。

因此 应该在0-无穷大之间,选择一个合适的数,平衡第一项和第二项。
4.4.3 用于线性回归的正则化方法
正则化线性回归的梯度下降算法:

4.4.4 用于逻辑回归的正则化方法
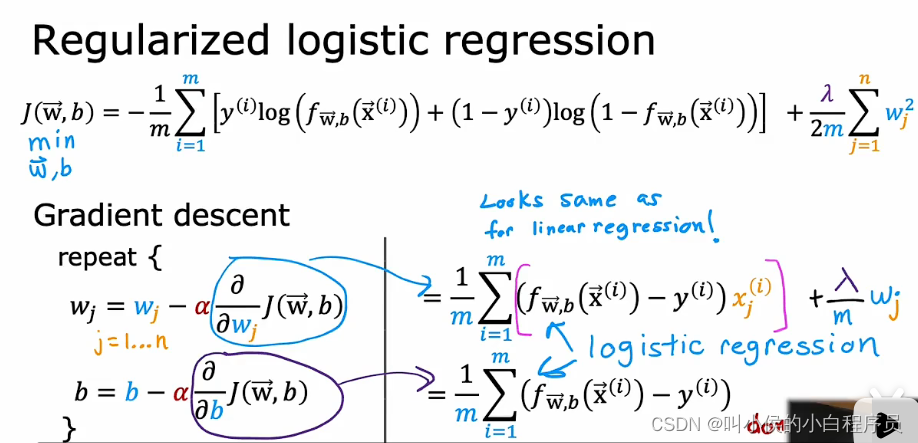
逻辑回归的正则化表示的成本函数:

正则化逻辑回归的梯度下降算法:
相关文章:

机器学习第一周
一、概述 机器学习大致会被划分为两类:监督学习,无监督学习 1.1 监督学习 监督学习其实就是,给计算机一些输入x和正确的输出y(训练数据集),让他总结x->y的映射关系,从而给他其他的输入x&a…...

大数据采集技术与预处理学习一:大数据概念、数据预处理、网络数据采集
目录 大数据概念: 1.数据采集过程中会采集哪些类型的数据? 2.非结构化数据采集的特点是什么? 3.请阐述传统的数据采集与大数据采集的区别? 4.大数据采集的数据源有哪些?针对不同的数…...

MySQL - 为什么索引结构默认使用B+树,而不是其他?
B-Tree的缺点: 范围查询效率相对较低:虽然B-Tree支持范围查询,但在实际操作中可能需要进行多次树遍历,性能较差。磁盘空间利用不高:B-Tree中的非叶子节点也存储数据,导致磁盘空间利用率相对较低。更复杂的平…...
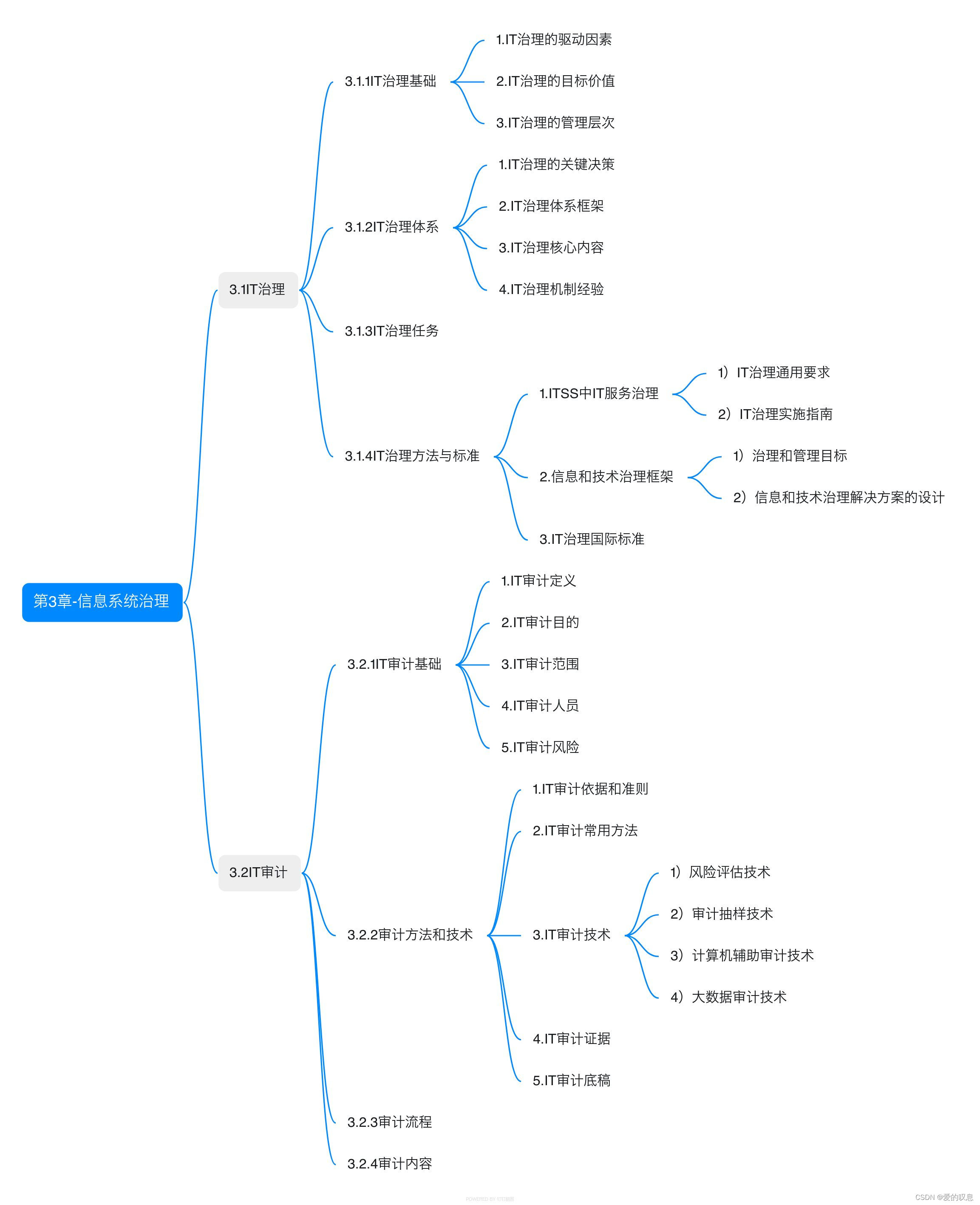
信息系统项目管理师教程 第四版【第3章-信息系统治理-思维导图】
信息系统项目管理师教程 第四版【第3章-信息系统治理-思维导图】...

2023.NET技术沙龙知识学习笔记
目录 一.Bootstrap Blazor UI组件库企业级应用介绍1.Blazor是什么2.为什么要用Blazor3.Bootstrap Blazor是什么 二.使用WebAssembly运行、扩展.NET应用程序1.WebAssembly简介2.WebAssembly的起源3.为什么选择二进制格式?4.WebAssembly与传统JavaScript的对比5.执行速…...
Golang教程——配置环境,再探GoLand
文章目录 一、Go是什么?二、环境配置验证配置环境变量 三、安装开发者工具GoLand四、HelloGolang 一、Go是什么? Go(也称为Golang)是一种开源的编程语言,由Google开发并于2009年首次发布。Go语言旨在提供一种简单、高…...

C++之lambda匿名、using、typedef总结【全】(二百四十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
基于SpringBoot的个人博客系统
基于SpringBootVue的个人博客系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 系统公告 博客详情 后台发文 摘要 基于Spring Boot的个人博客系统是一种…...

javascript中的继承
基本术语 本文中,proto [[Prototype]] 原型链 基本思想: 构造函数生成的对象有一个指针(proto)指向构造函数的原型。如果将构造函数1的原型指向另一个构造函数2的实例,则构造函数1的实例__proto__.proto 指向了构…...

智能问答技术在百度搜索中的应用
作者 | Xiaodong 导读 本文主要介绍了智能问答技术在百度搜索中的应用。包括机器问答的发展历程、生成式问答、百度搜索智能问答应用。欢迎大家加入百度搜索团队,共同探索智能问答技术的发展方向,文末有简历投递方式。 全文6474字,预计阅读时…...

STM32F4X SDIO(一) SD卡介绍
STM32F4X SDIO(一) SD卡介绍 SD卡分类外观分类容量分类传输速度分类 在之前的章节中,讲过有关嵌入式的存储设备,有用I2C驱动的EEPROM、SPI驱动的FLASH和MCU内部的FLASH,这类存储设备的优点是操作简单,但是缺…...
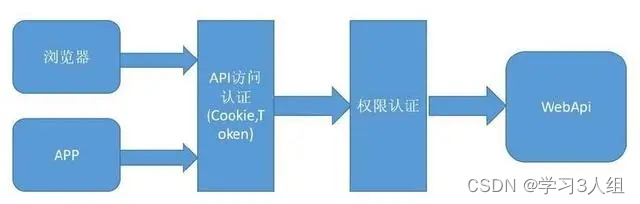
10分钟了解JWT令牌 (JSON Web)
10分钟了解JSON Web令牌(JWT) JSON Web Token(JWT)是目前最流行的跨域身份验证解决方案。今天给大家介绍JWT的原理和用法。 1.跨域身份验证 Internet服务无法与用户身份验证分开。一般过程如下。 1.用户向服务器发送用户名和密码。…...

【经验总结】ECU系统休眠后通过诊断报文唤醒ECU且唤醒网络后快发NM报文
目录 前言 正文 1.CanNM状体机分析 2.ComM状态机分析 3.解决方案 4.总结 前言...

基于Android 10系统的ROC-RK3399-PC Pro源码编译
基于Android 10系统的ROC-RK3399-PC Pro源码编译 一、开发环境搭建二、下载Android 10 SDK三、编译Android 10 SDK ROC-RK3399-PC Pro资料下载处:https://www.t-firefly.com/doc/download/145.html一、开发环境搭建 Android 10 SDK的编译对PC机的要求不低ÿ…...

网络滤波器/网络滤波器/脉冲变压器要怎样进行测试,一般要测试哪些参数?
Hqst华强盛导读:网络滤波器/网络滤波器/脉冲变压器要怎样进行测试,一般要测试哪些参数?测试网络滤波器的测试方法和步骤如何,需用到哪些测试工具和仪器设备呢? 一,网络流量的监控和过滤能力测试&am…...
基于vue天气数据可视化平台
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Go 语言常见的 ORM 框架
ORM(Object-Relational Mapping)是一种编程技术,用于将面向对象编程语言中的对象模型和关系数据库中的数据模型相互映射。ORM框架可以把数据操作从 SQL 语句中抽离出来,将关系型数据库中的表映射成对象,通过面向对象的…...

【错误解决方案】ModuleNotFoundError: No module named ‘cPickle‘
1. 错误提示 在python程序中试图导入一个名为cPickle的模块,但Python提示找不到这个模块。 错误提示:ModuleNotFoundError: No module named cPickle 2. 解决方案 实际上,cPickle是Python的pickle模块的一个C语言实现,通常用于…...

NodeJS14.18.0 安装,以及安装相应版本node-sass
安装了NVM, NodeJS 14.18.0 安装nvm 到c:\nvm目录 务必!!!!!!!! nvm文档手册 - nvm是一个nodejs版本管理工具 - nvm中文网 编辑c:\nvm\settings.txt添加 node_mirror: CNPM Binar…...
cosover是什么?crossover23又是什么软件
cosover是篮球里的过人技巧。 1.crossover在篮球中的本意是交叉步和急速交叉步。crossover 是篮球术语,有胯下运球、双手交替运球,交叉步过人、急速大幅度变向等之意。 2.在NBA里是指包括胯下运球、变向、插花在内的过人的技巧。 NBA有很多著名的Cross…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
