【ARMv8 SIMD和浮点指令编程】NEON 通用数据处理指令——复制、反转、提取、转置...
NEON 通用数据处理指令包括以下指令(不限于):
• DUP
将标量复制到向量的所有向量线。
• EXT
提取。
• REV16、REV32、REV64
反转向量中的元素。
• TBL、TBX
向量表查找。
• TRN
向量转置。
• UZP、ZIP
向量交叉存取和反向交叉存取。
1 DUP (element)
将向量元素复制为向量或标量。该指令将源 SIMD&FP 寄存器中指定元素索引处的向量元素复制为标量或向量中的每个元素,并将结果写入目标 SIMD&FP 寄存器。
标量

DUP <V><d>, <Vn>.<T>[<index>]
向量

DUP <Vd>.<T>, <Vn>.<Ts>[<index>]
<T> :
对于标量变体,是元素宽度说明符,以“imm5”编码:
| imm5 |
|---|
相关文章:

【ARMv8 SIMD和浮点指令编程】NEON 通用数据处理指令——复制、反转、提取、转置...
NEON 通用数据处理指令包括以下指令(不限于): • DUP 将标量复制到向量的所有向量线。 • EXT 提取。 • REV16、REV32、REV64 反转向量中的元素。 • TBL、TBX 向量表查找。 • TRN 向量转置。 • UZP、ZIP 向量交叉存取和反向交叉存取。 1 DUP (element) 将…...
C#,数值计算——分类与推理,基座向量机的 Svmgenkernel的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public abstract class Svmgenkernel { public int m { get; set; } public int kcalls { get; set; } public double[,] ker { get; set; } public double[] y { get; set…...
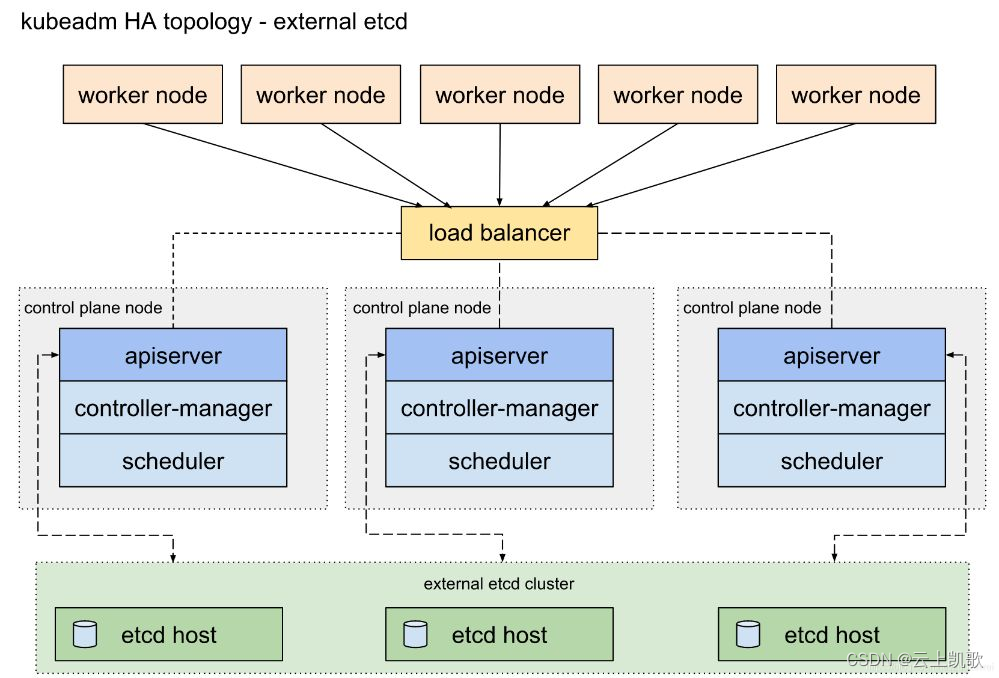
08.K8S高可用方案
K8S高可用方案 1、高可用部署方式 官方提供两种高可用实现方式: 堆叠etcd 拓扑,其中 etcd 节点与控制平面节点共存;外部 etcd 节点,其中 etcd 与控制平面在不同的节点上运行;1.1、堆叠 etcd 拓扑 主要特点: 每个 master 节点上运行一个 apiserver 和 etcd, etcd 只与本…...
MySQL实战1
文章目录 主要内容一.墨西哥和美国第三高峰1.准备工作代码如下(示例): 2.目标3.实现代码如下(示例): 4.相似例子代码如下(示例): 二.用latest_event查找当前打开的页数1.准备工作代码如下(示例&…...

关于A level的习题答案
CAIE考试局(也称为CIE) 的真题答案有本书叫做《A-level 数学历年真题全解》包含2015-2019的Paper1、Paper3、Paper4、Paper6 Further Mathematica cousebook这本书的最后有Answer但是没有过程 Edexcel考试局 书本末尾有简易答案。 但是具体答案在Sol…...

左神算法题系列:动态规划机器人走路
机器人走路 假设有排成一行的N个位置记为1~N,N一定大于或等于2 开始时机器人在其中的start位置上(start一定是1~N中的一个) 如果机器人来到1位置,那么下一步只能往右来到2位置; 如果机器人来到N位置,那么下一步只能往左来到N-1位…...

LeetCode75——Day19
文章目录 一、题目二、题解 一、题目 724. Find Pivot Index Given an array of integers nums, calculate the pivot index of this array. The pivot index is the index where the sum of all the numbers strictly to the left of the index is equal to the sum of all…...
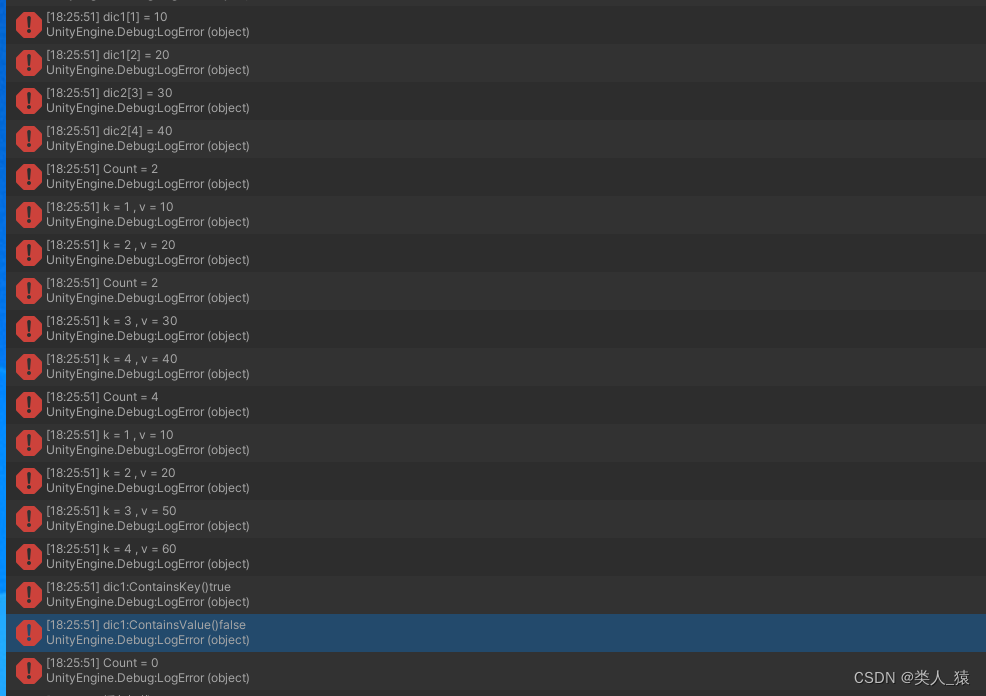
ToLua使用原生C#List和Dictionary
ToLua是使用原生C#List 介绍Lua中使用原生ListC#调用luaLua中操作打印测试如下 Lua中使用原生DictionaryC#调用luaLua中操作打印测试如下 介绍 当你用ToLua时C#和Lua之间肯定是会互相调用的,那么lua里面使用List和Dictionary肯定是必然的,在C#中可以调用…...

WebDAV之π-Disk派盘 + 言叶
言叶是一个功能丰富的笔记软件,为跨平台而设计,可以为你在手机、电脑和其他设备中实现多端同步。从而实现高效率的记事和办公。支持Markdown的语言和多种计算机语法高亮功能,让你笔记中的内容更加主次分明,可以在这里记录一些代码什么的。同时还可以在笔记中插入图片,使其…...

Spring Security: 整体架构
Filter Spring Security 是基于 Sevlet Filter 实现的。下面是一次 Http 请求从 client 出发,与 Servlet 交互的图: 当客户端发送一个请求到应用,容器会创建一个 FilterChain,FilterChain 中包含多个 Filter 和 Servlet。这些 Fi…...

JavaScript进阶知识汇总~
JavaScript 进阶 给大家推荐一个实用面试题库 1、前端面试题库 (面试必备) 推荐:★★★★★ 地址:web前端面试题库 1.原型链入门 1) 构造函数 当我们自定义一个函数时(箭头函数与生成器函数除外),这个函…...

理解C#中对象的浅拷贝和深拷贝
本文章主要介绍C#中对象的拷贝,其中包括浅拷贝和深拷贝,以及浅拷贝和深拷贝的实现方式,不同的实现方式之间的性能对比。 1、浅拷贝和深拷贝 浅拷贝是指将对象中的数值类型的字段拷贝到新的对象中,而对象中的引用型字段则指复制它…...
)
js 生成随机数(含随机颜色)
生成 0-1 之间的随机数 Math.random()生成 0-x 之间的随机整数: Math.round(Math.random()*x)生成 min-max 之间的随机整数: Math.round(Math.random()*(max-min)min)生成N位随机数 /*** 函数--生成N位随机数* param {*} N 数字的长度*/ function random…...
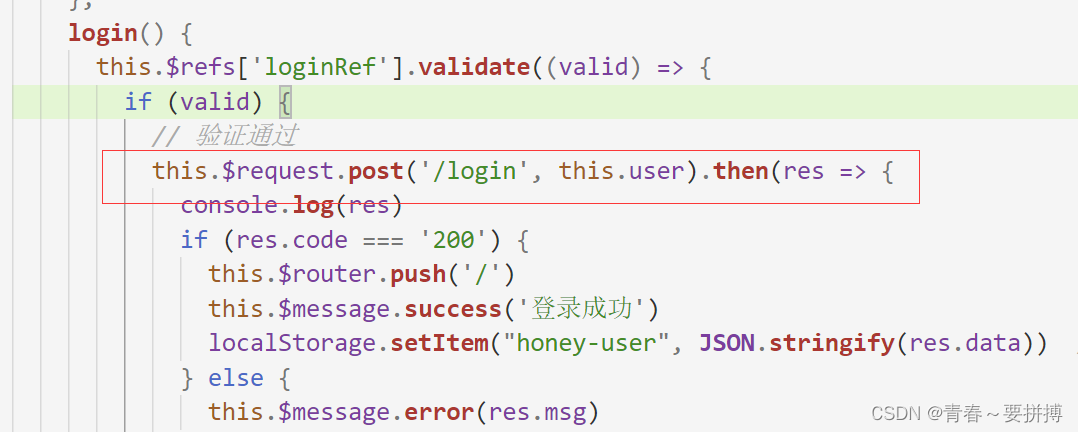
【axios】axios的基本使用
一、 Axios简介 1、 Axios是什么? Axios是一个基于promise的HTTP库,类似于jQuery的ajax,用于http请求。可以应用于浏览器端和node.js,既可以用于客户端,也可以用于node.js编写的服务端。 2.、Axios特性 支持Promis…...

React 在非组件环境切换路由
我的react-router-dom版本是6.16.0。之前在react中是这样配置路由的 App.jsx import ReactDOM from react-dom/client; import { HashRouter, Route, Routes } from react-router-dom;const root ReactDOM.createRoot(document.getElementById("app")); root.rend…...

Oracle高速批量速插入数据解决方案
最近做短信群发项目有一个需求,需要客户大批量(十万级)导入数据. 开始是用insert单条数据,10万条数据要20分钟 后来发现可以用insert all 一条sql一次导入500条记录,这样10万条数据只用了1.5分钟,导入速度提高了近来20倍 下面就使用insert all的心得体会记录如下. 使用方法: i…...
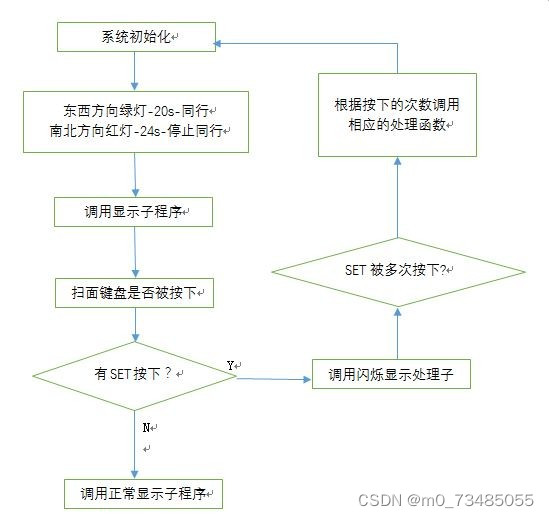
基于单片机嵌入式的智能交通信号灯管理系统的设计与实现
项目介绍 有目共睹电子设备已经席卷了整个人类生活,他们不断改善着人们的起居住行,这也就促进了嵌入式人工智能的快速发展。 本课设模拟系统分为软硬件两部分组成。硬件部分是由两位8段数码管和LED灯构成的显示系统和控制电路等组成,能较好的…...
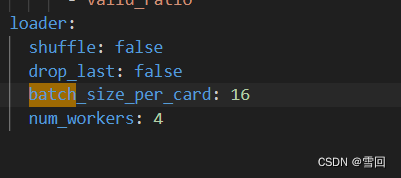
在全新ubuntu上用gpu训练paddleocr模型遇到的坑与解决办法
目录 一. 我的ubuntu版本二.首先拉取paddleocr源代码三.下载模型四.训练前的准备1.在源代码文件夹里创造一个自己放东西的文件2.准备数据2.1数据标注2.2数据划分 3.改写yml配置文件4.…...

React之服务端渲染
一、是什么 在SSR中 (opens new window),我们了解到Server-Side Rendering ,简称SSR,意为服务端渲染 指由服务侧完成页面的 HTML 结构拼接的页面处理技术,发送到浏览器,然后为其绑定状态与事件,成为完全可…...
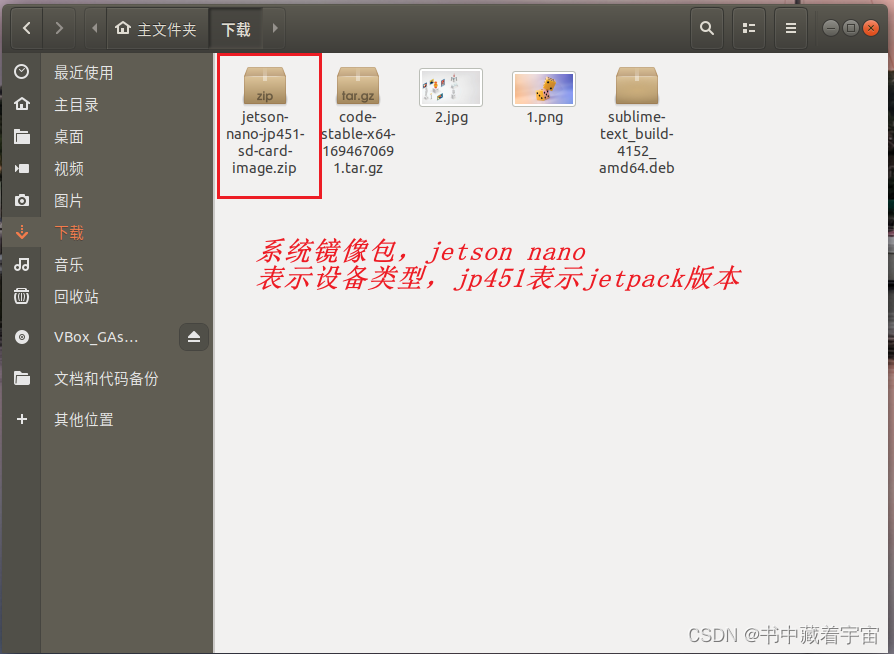
jetson nano刷机更新Jetpack
只是记录个人在使用英伟达jetson Nano的经历,由于头一次尝试,所以特此记录需要的问题和经验。 一,英伟达刷机教程(jetson nano 版本) 本次我是直接刷机到TF卡,然后TF卡作为启动盘进行启动,我看网上有带EMMC版本的,好像可以直接把系统镜像安装到EMMC里面。但是有个问题…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
