【通信原理】第一章|绪论|信息度量和通信系统的性能指标
前言
那么这里博主先安利一些干货满满的专栏了!
首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。
- 高质量博客汇总
绪论
1. 信息和信息的度量
定义信息的度量。
I = log a 1 P ( x ) = − log a P ( x ) I=\log _{a} \frac{1}{P(x)}=-\log _{a} P(x) I=logaP(x)1=−logaP(x)
当 a = 2 a=2 a=2当时候,信息量大单位为(bit),当 a = e a=e a=e当是时候,信息量的单位为(nat),若 a = 10 a=10 a=10,信息量大单位为哈特莱(Hartley)。
对于离散信源,M个波形等概率 P = 1 / M P=1/M P=1/M发送,且每个波形出现是独立的,即信源是无记忆的,则传送M进制波形之一的信息量为。
I = log 2 1 P = log 2 1 1 / M = log 2 M I=\log _{2} \frac{1}{P}=\log _{2} \frac{1}{1 / M}=\log _{2} M I=log2P1=log21/M1=log2M
如果M是2的整数次幂,比如 M = 2 k M=2^k M=2k,则式子可以改写成 I = k I=k I=k。
2. 通信系统主要性能指标
频带利用率。
η = R B B ( Baud / H z ) \eta=\frac{R_{\mathrm{B}}}{B} \quad(\text { Baud } / \mathrm{Hz}) η=BRB( Baud /Hz)
或
η b = R b B ( b / ( s ⋅ H z ) ) \eta_{\mathrm{b}}=\frac{R_{\mathrm{b}}}{B} \quad(\mathrm{~b} /(\mathrm{s} \cdot \mathrm{Hz})) ηb=BRb( b/(s⋅Hz))
R B R_B RB为码原传输速率,简称传码率,也可以叫做波特率。
设每个码元的长度为 T B ( s ) T_B(s) TB(s),则有
R B = 1 T B ( B a u d ) R_B = \frac{1}{T_B} \quad (Baud) RB=TB1(Baud)
R b R_b Rb为信息传输速率,简称传信率,也可以叫做比特率。
因为一个M进制码元携带 l o g 2 M log_2M log2M比特的信息量,所以码元速率和信息速率有以下确定的关系,即。
R b = R B log 2 M ( b / s ) R B = R b log 2 M ( B a u d ) R_{\mathrm{b}}=R_{\mathrm{B}} \log _{2} M \quad(b/s) \\ R_{\mathrm{B}}=\frac{R_{\mathrm{b}}}{\log _{2} M} \quad (Baud) Rb=RBlog2M(b/s)RB=log2MRb(Baud)
如果二进制码元的持续时间为 T b T_b Tb,则 T b T_b Tb与 T B T_B TB有如下关系。
T B = T b ⋅ l o g 2 M T_B = T_b \cdot log_2M TB=Tb⋅log2M
误码率。
P e = 错误码元数 传输总码元数 P_e = \frac{错误码元数}{传输总码元数} Pe=传输总码元数错误码元数
误信率。
P b = 错误比特数 传输总比特数 P_b = \frac{错误比特数}{传输总比特数} Pb=传输总比特数错误比特数
相关文章:

【通信原理】第一章|绪论|信息度量和通信系统的性能指标
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 绪论 1. 信息和信息的度量 定义信息…...
)
基于STM32+OneNet设计的物联网智能鱼缸(2023升级版)
基于STM32+OneNet设计的智能鱼缸(升级版) 一、前言 随着物联网技术的快速发展,智能家居和智能养殖领域的应用越来越广泛。智能鱼缸作为智能家居和智能养殖的结合体,受到了越来越多消费者的关注。本项目设计一款基于STM32的物联网智能鱼缸,通过集成多种传感器和智能化控制模…...
NET-MongoDB的安装使用
一.下载 MongoDB 点击 Select package 选择自己所需版本后点击下载,本文选用Windows 6.0版本以上 二、配置MongoDB 在 Windows 上,MongoDB 将默认安装在 C:\Program Files\MongoDB 中。 将 C:\Program Files\MongoDB\Server\version_numbe…...
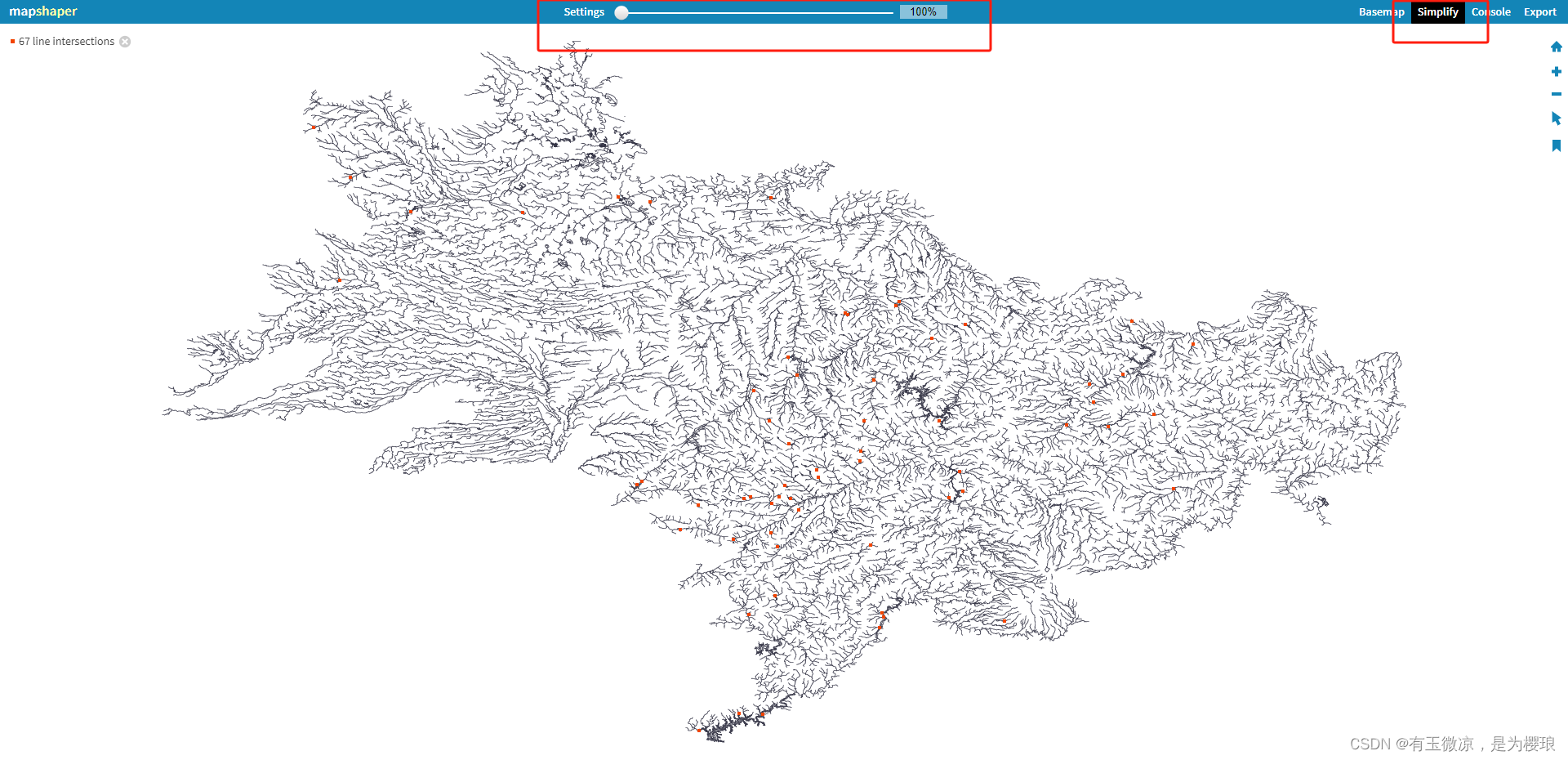
简化geojson策略
1、删除无用的属性,也就是字段,在shp的时候就给删了 用arcgis等等软件都可以做到 2、简化坐标的小数位数 (1)网上推荐的办法,俺不会Python… github.com/perrygeo/geojson-precision (2)曲线…...
:Binder进程和线程的创建)
一个Binder的前生今世 (二):Binder进程和线程的创建
文章目录 一个Binder的前生今世 (二):Binder进程和线程的创建binder在进程中的启动小结注释一个Binder的前生今世 (二):Binder进程和线程的创建 前篇文章一个Binder的前生今世 (一):Service的创建 讲了一个Service是如何创建以及如何与客户端建立联系的。讲解中涉及到…...

RocketMq源码分析(八)--消息消费流程
文章目录 一、消息消费实现二、消息消费过程1、消息拉取2、消息消费1)提交消费请求2)消费消息 一、消息消费实现 消息消费有2种实现,分别为:并发消费实现(ConsumeMessageConcurrentlyService)和顺序消费实现…...
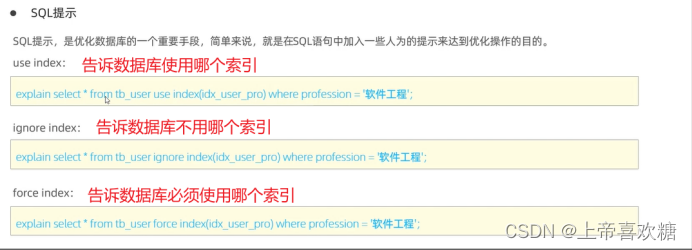
sql--索引使用
最左前缀法则(联合索引) 联合索引 位置不影响,但是所有索引必须连续使用,才会走索引 中间跳过则会造成后面索引则会失效 索引失效 规避方法---尽量使用> 或 < Explain需要重点关注的字段 Type key_leng possibl…...
-- Map、List ==》JSON字符串)
alibaba.fastjson的使用(三)-- Map、List ==》JSON字符串
目录 1.使用到的方法为: 2. Map转JSON字符串 3. List转JSON字符串 1.使用到的方法为: static String toJSONString(Object object) 2. Map转JSON字符串 /**...
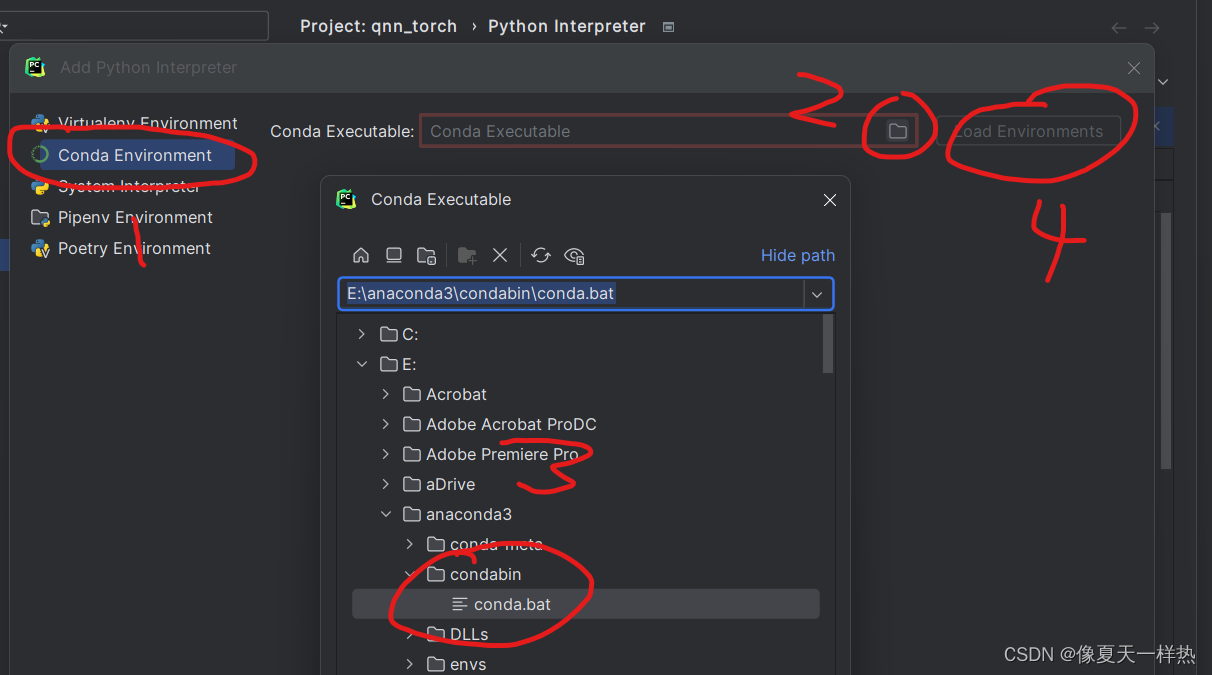
pycharm 2023.2.3设置conda虚拟环境
分两步: (1)设置Virtualenv Environment (2)设值Conda Executable 加载conda环境,然后选择conda环境...

安卓Frida 脱壳
总结下现在脱壳的方法,比如寒冰大佬的Fart,买Nexus 手机,然后刷入肉丝老师的镜像就可以。是比较快速的方式。我今天推荐的方式是,使用Frida 来脱壳,基本上满足日常需求。也不用特别准备手机,脱壳镜像等。 Frida 环境电脑端安装比较简单,主要注意和手机版本相同即可。手机…...

【C】为什么7.0会被存储为6.99999
在《C Primer Plus》第 6 版 3.3.3 节 浮点数的介绍中,作者说浮点数通常只是实际值的近似值,例如,7.0可能被储存为浮点值6.99999。 如果采用32位的IEEE 754浮点表示形式来存储7.0,那么它的二进制表示将如下: 符号位&…...

Framework -- 系统架构
一、前言 framework的学习,需要掌握到什么程度? App 的启动流程:整体的过程,具体到某些类在整个流程中所起的作用;组件的设计模式,核心设计思想;需要知晓目前已知的问题,以及解决方…...

1.1 计算机安全概念
思维导图: 前言: 第1章: 计算机与网络安全概念笔记 1. 学习目标 了解保密性、完整性和可用性的关键安全需求。了解OSI的X.800安全架构。识别和举例说明不同的安全威胁和攻击。掌握安全设计的基本准则。熟悉攻击面和攻击树的使用。了解与密码标准相关的…...

react中的函数柯里化
函数柯里化是一种将接受多个参数的函数转化为一系列接受单一参数的函数的技术。在React开发中,函数柯里化可以帮助我们更好地组织组件的代码,使其具有更好的可读性和可复用性。 一个简单的函数柯里化示例: function add(a) {return functio…...

Unity点乘的实战案例1
向量的点乘,也叫向量的内积、数量积,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。点乘,也叫数量积。结果是一个向量在另一个向量方向上投影的长度,是一个标量。 • …...

Hive数据查询详解
本专栏案例数据集链接: https://download.csdn.net/download/shangjg03/88478038 1.数据准备 为了演示查询操作,这里需要预先创建三张表,并加载测试数据。 1.1 员工表 -- 建表语句CREATE TABLE emp(empno INT, -- 员工表编号ename STRING, -- 员工姓名...
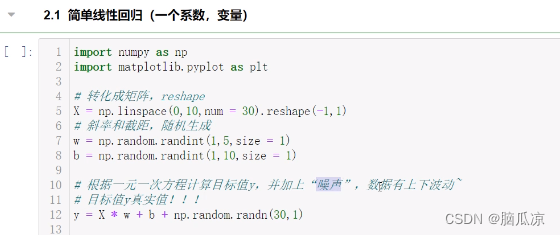
人工智能基础_机器学习008_使用正规方程_损失函数进行计算_一元一次和二元一次方程演示_sklearn线性回归演示---人工智能工作笔记0048
自然界很多都是正态分布的,身高,年龄,体重...但是财富不是. 然后我们来看一下这个y = wx+b 线性回归方程. 然后我们用上面的代码演示. 可以看到首先import numpy as np 导入numby 数据计算库 import matplotlib.pyplot as plt 然后导入图形画的库 然后: X = np.linspace(0,…...
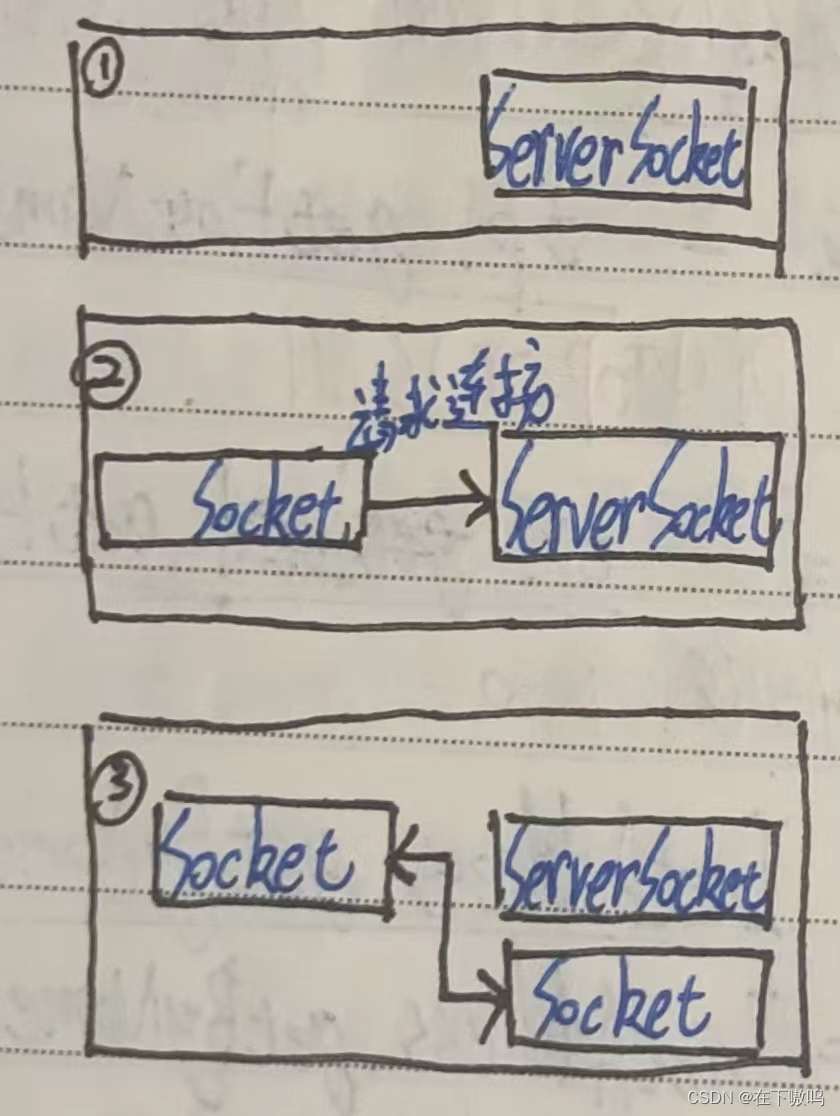
【详细】Java网络通信 TCP、UDP、InetAddress
一、网络程序设计基础 1.局域网与因特网 为了实现两台计算机的通信,必须用一个网络线路连接两台计算机(服务器<-->网络<-->客户机)。 服务器是指提供信息的计算机或程序,客户机是指请求信息的计算机或程序。网络用…...
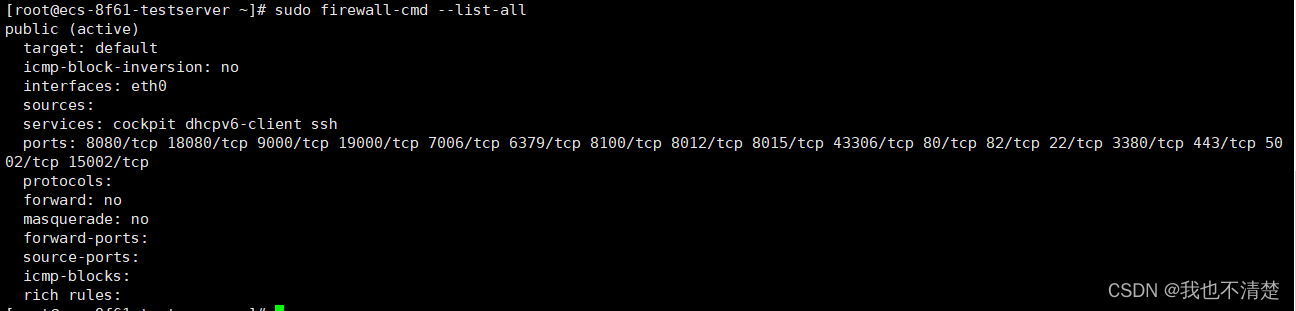
Linux(Centos7)操作记录
1、nginx -t #Nginx配置文件检查 上述截图代表检查没问题 上述截图检查配置文件配置错误,并提示错误文件位置 2、systemctl restart nginx #重启Nginx 重启Nginx失败 3、systemctl status nginx.service #查看Nginx服务状态 80端口被占导致服务启动失败 4、n…...
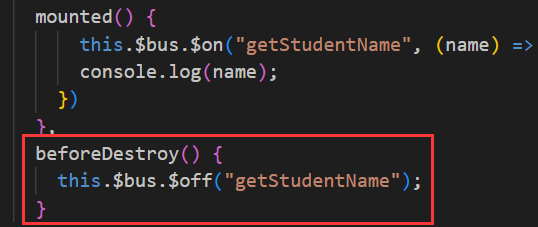
Vue全局事件总线实现任意组件间通信
一、安装全局事件总线 全局事件总线就像是一个工具,专门用于挂载自定义事件和。 想要所有的组件都能使用这个全局事件总线,就只有在Vue的原型身上添加一个能够绑定自定义事件的属性。 所以我们在创建Vue实例对象的时候就可以添加如下代码:…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
