CTF-Crypto学习记录-第四天 “ “ --- SHA1安全散列算法,实现原理。
文章目录
- 前言
- SHA-1加密算法介绍
- 关于SHA-1和MD5
- SHA-1 加密过程
- 原文处理
- 设置初始值和数据结构定义
- 加密运算原理过程
- 在python中调用SHA-1
前言
MD5学习MD5加密算法
SHA-1加密算法介绍
SHA-1(Secure Hash Algorithm1,安全散列算法1)是一种密码散列函数。
SHA-1可以生成一个被称为消息摘要的160位(20字节)散列值,散列值通常的呈现形式为40个十六进制数。
SHA-1的历史:
2005年,密码分析人员发现了对SHA-1的有效攻击方法,这表明该算法可能不够安全,不能继续使用,自2010年以来,许多组织建议用SHA-2或SHA-3来替换SHA-1。Microsoft、Google以及Mozilla都宣布,它们旗下的浏览器将在2017年停止接受使用SHA-1算法签名的SSL证书。
2017年2月23日,CWI Amsterdam与Google宣布了一个成功的SHA-1碰撞攻击,发布了两份内容不同但SHA-1散列值相同的PDF文件作为概念证明。
2020年,针对SHA-1的选择前缀冲突攻击已经实际可行。建议尽可能用SHA-2或SHA-3取代SHA-1。
关于SHA-1和MD5
在上一篇学习笔记里学了MD5加密算法,SHA-1和MD5同样是哈希函数,俩者对于任意长度明文的预处理也都是相同的,那么俩者有什么不同呢?
- 摘要长度 (安全性)
SHA-1所产生的摘要是160位比MD5产生的摘要长32位,因此在安全性上SHA-1高于MD5。 - 运算速度
同样因为,SHA-1的摘要长于MD5,运算步骤也比MD5多了16步,因此运算速度要慢于MD5
关于MD5和SHA-1,在如今现代计算环境中都已经不再被认为是安全的哈希函数了,为了保证数据和应用的安全,应该使用SHA-256或SHA-3等算法。
SHA-1 加密过程
同MD5一样,可以分为三个过程:
原文处理
对于任意长度明文,需要先进行填充处理,使得明文长度为448(mod 512)位,有俩种情况:
- 原始明文长度mod512不为448,需要进行填充;这里假设原始明文一共有b bit,那就在b+1 bit处填充一个1,后面全部填充0,直到明文长度mod512等于448为止。
- 第二种情况,原始明文长度mod512正好为448,这种情况也需要进行填充,总共填充512位的数据,直到明文再次mod512等于448为止。
因此填充的数据长度最小为1 bit ,最大为512 bit。‘
’
再得到448bit长度的明文后,还需要添加64bit的数据,使得明文长度等于512 bit。
填充处理完成之后是分组处理:
要先将恰好为512整数倍的明文,分成 L 个512 bit长度 的明文分组。接下来对每个512 bit大小的明文分组进行类似于MD5的操作;
- 先将512 bit 的明文分组,分成 16个 32 bit的子明文分组。可以用 M[k] 表示
- 之后再将这16个子明文分组扩展到 80个子明文分组。 可以用W[k]表示
扩充的方式如下:
W t = M t , 当0≤t≤15
W t = ( W t-3 ⊕ W t-8⊕ W t-14⊕ W t-16 ) <<< 1, 当16≤t≤79
设置初始值和数据结构定义
一些相关定义:
SHA 1 针对输入的比特流是按块 (block) 依次进行处理的, 每个块的长度固定为 512 bit, SHA 1 算法允许的最大输入长度为 2^64−1 bit, 在 SHA 1 算法中, 我们将 32 bit 定义为字 (word), 所以每个字可以用 8 位十六进制来表示, 例如对于字 1010 0001 0000 0011 1111 1110 0010 0011 可表示为 A103FE23, 对于一个长度在 [0, 2^32−1] 的整数便可以用一个字来表示, 整数的最低有效 4 位为字的最右侧的十六进制字符, 对于一个整数 z, 若 0≤z<2^64 则 z=(2^32*x+y), 其中 0≤x,y<2^32, 于是 x, y都分别可以用一个字来表示, 我们记这两个字分别为 X, Y, 此时整数 z 便可以使用这对字来表示, 我们记为 (X,Y)
可以将针对bit 的逻辑运算符扩展定义到字上;
X AND Y 为两个字按位逻辑与
X OR Y 为两个字按位逻辑或
X XOR Y 为两个字按位异或
NOT X 为对字 X 的每一位按位取反
除了逻辑运算符,还可以定义字上的算术运算,
X + Y 定义为 (x + y) mod 2^32
最后定义字上的循环左移运算符(逻辑移位),循环左移即是将字的比特整体向左移动 n 位, 左侧溢出的比特位补到右侧空出来的比特位, 我们将这一运算记作 S^n(X), 循环左移可以使用逻辑表达式来描述, 如下所示:
S^n(X) = (X << n) OR (X >> 32 -n)
MD5中有4个初始变量值,而SHA-1中有五个链接变量,如下:
H0=0x67452301H1=0xEFCDAB89H2=0x98BADCFEH3=0x10325476H4=0xC3D2E1F0
此外 SHA-1定义了4个逻辑函数和4个常量。每个逻辑函数针对3个字作为输入,函数的输出为一个字,其中 t (0 ≤ t ≤ 79) 是变量, 函数的表达式如下:
f(t;B,C,D) = (B AND C) OR ((NOT B) AND D) ( 0 <= t <= 19)f(t;B,C,D) = B XOR C XOR D (20 <= t <= 39)f(t;B,C,D) = (B AND C) OR (B AND D) OR (C AND D) (40 <= t <= 59)f(t;B,C,D) = B XOR C XOR D (60 <= t <= 79)
4个常量分别如下(十六进制表示):
K(t) = 5A827999 ( 0 <= t <= 19)K(t) = 6ED9EBA1 (20 <= t <= 39)K(t) = 8F1BBCDC (40 <= t <= 59)K(t) = CA62C1D6 (60 <= t <= 79)
加密运算原理过程
SHA1有4轮运算,每一轮包括20个步骤,一共80步。
下图是 SHA-1算法中的一个回圈;
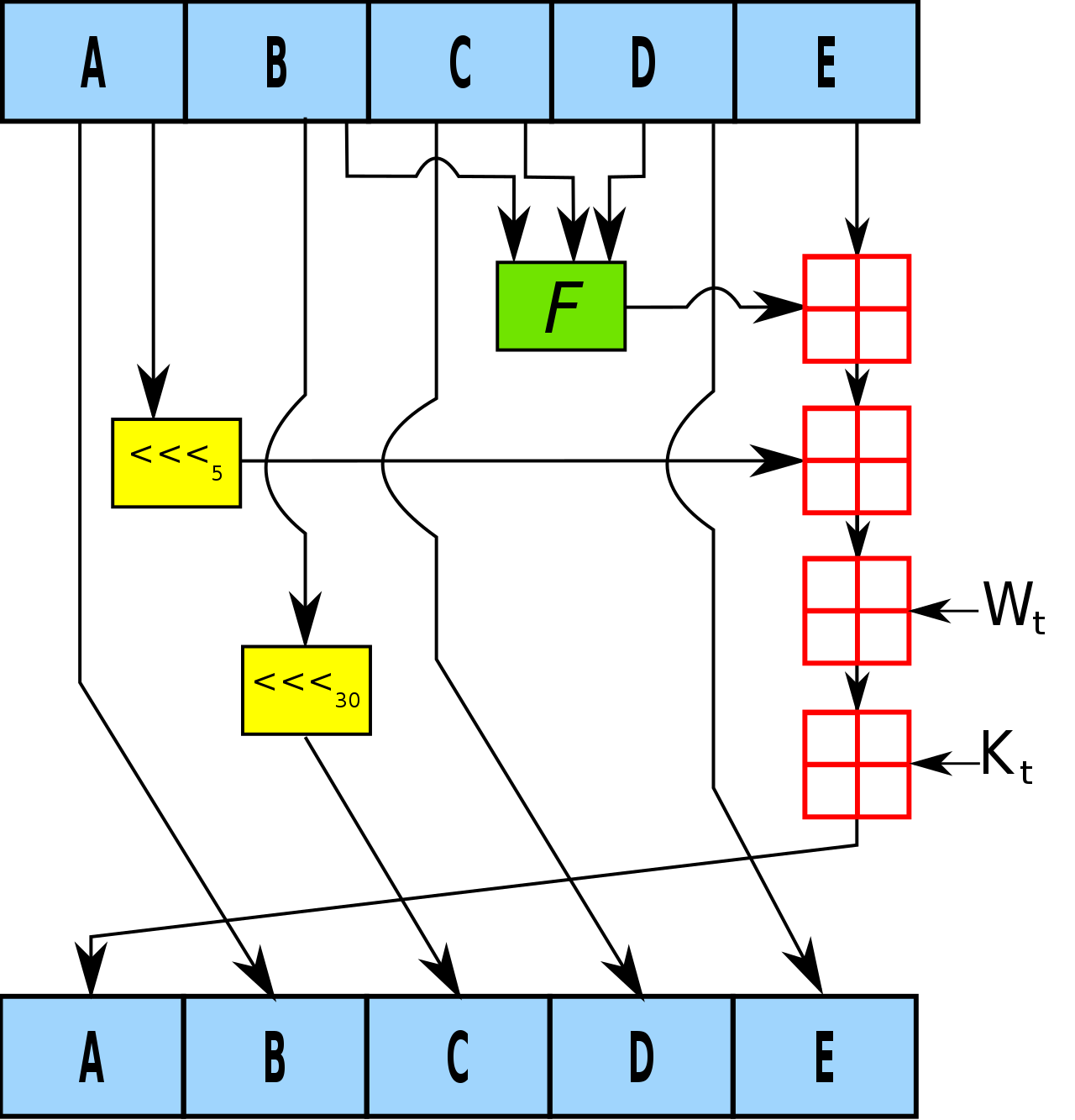
- 也如MD5一样,SHA-1会现将H0,H1,H2,H3,H4,H5五个初始变量依次放入ABCDE中;即 A = H0, B = H1, C = H2, D = H3, E = H4
- 定义循环变量 t, 对 t 从 0 到 79 依次赋值, 每一次循环执行如下操作:
- TEMP = S^5(A) + f(t;B,C,D) + E + W(t) + K(t);
- E = D;
- D = C;
- C = S^30(B);
- B = A;
- A = TEMP;
- 分别令 H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E
从 M(0) 开始每一轮计算后会得到新的 H0, H1, … , H4, 下一轮计算中使用上一次产生的新值, 对最后一个块计算完毕后得到的 H0, H1, … , H4便是算法的输出, 即原文的 SHA 1 哈希值
在python中调用SHA-1
import hashlib# 要哈希的数据
data = b'Hello, World!' # 在 Python 3 中,请确保数据以字节字符串的形式表示# 创建一个 SHA-1 哈希对象
sha1 = hashlib.sha1()# 更新哈希对象以处理数据
sha1.update(data)# 获取 SHA-1 哈希值的十六进制表示
sha1_hash = sha1.hexdigest()print("SHA-1 哈希值:", sha1_hash)
输出:
SHA-1 哈希值: 0a0a9f2a6772942557ab5355d76af442f8f65e01
文献参考:
https://www.cnblogs.com/scu-cjx/p/6878853.html
https://sunyunqiang.com/blog/sha1/
https://zh.wikipedia.org/zh-hans/SHA-1
相关文章:

CTF-Crypto学习记录-第四天 “ “ --- SHA1安全散列算法,实现原理。
文章目录 前言SHA-1加密算法介绍关于SHA-1和MD5 SHA-1 加密过程原文处理设置初始值和数据结构定义加密运算原理过程 在python中调用SHA-1 前言 MD5学习MD5加密算法 SHA-1加密算法介绍 SHA-1(Secure Hash Algorithm1,安全散列算法1)是一种密…...

海南海口大型钢结构件3D扫描全尺寸三维测量平面度平行度检测-CASAIM中科广电
高精度三维扫描技术已经在大型工件制造领域发挥着重要作用,特别是在质量检测环节,高效、高精度,可以轻松实现全尺寸三维测量。本期,CASAIM要分享的应用是在大型钢结构件的关键部位尺寸及形位公差检测。 钢结构件,是将…...

【PyQt学习篇 · ④】:QWidget - 尺寸操作
文章目录 QWidget简介QWidget大小位置操作案例一案例二 QWidget尺寸限定操作案例 内容边距案例 QWidget简介 在PyQt中,QWidget是一个基本的用户界面类,用于创建可见的窗口组件。QWidget可以包含多种类型的子组件,如QPushButton、QLabel、QLi…...
APC学习记录
文章目录 APC概念APC插入、执行过程逆向分析插入过程执行过程总结 代码演示参考资料 APC概念 APC全称叫做异步过程调用,英文名是 Asynchronous Procedure Call,在进行系统调用、线程切换、中断、异常时会进行触发执行的一段代码,其中主要分为…...
前端将图片储存table表格中,页面回显
<el-table :data"tableData" v-loading"loading" style"width: 100%" height"calc(100vh - 270px)" :size"tableSize"row-dblclick"enterClick"><el-table-column prop"name" label"文档…...

[论文阅读]Ghost-free High Dynamic Range Imaging with Context-aware Transformer
多帧高动态范围成像(High Dynamic Range Imaging, HDRI/HDR)旨在通过合并多幅不同曝光程度下的低动态范围图像,生成具有更宽动态范围和更逼真细节的图像。如果这些低动态范围图像完全对齐,则可以很好地融合为HDR图像,但…...
例子效果)
react高阶成分(HOC)例子效果
使用React函数式组件写了一个身份验证的一个功能,示例通过高阶组件实现的一个效果展示: import React, { useState, useEffect } from react;// 定义一个高阶组件,它接受一个组件作为输入,并返回一个新的包装组件 const withAuth…...
)
【24种设计模式】工厂模式(Factory Pattern)
工厂模式是一种创建型设计模式,它提供了一种创建对象的方式,而无需暴露对象创建的逻辑。在这篇博客中,我们将介绍工厂模式的概念、使用场景以及示例代码。 概念 工厂模式是一种创建型设计模式,它提供了一种创建对象的方式&#…...

树——对称二叉树
leetcode题目地址 树为空树,亦为对称二叉树树非空时,仅需判断其左右子树是否对称判断左右子树对称 (1) 左右子树是否为空,有一个为空 便不对称, 都为空或都不为空 可能对称 (2) 左右子树根节点值是否相同 (3) 判断 左子树 的 左子…...
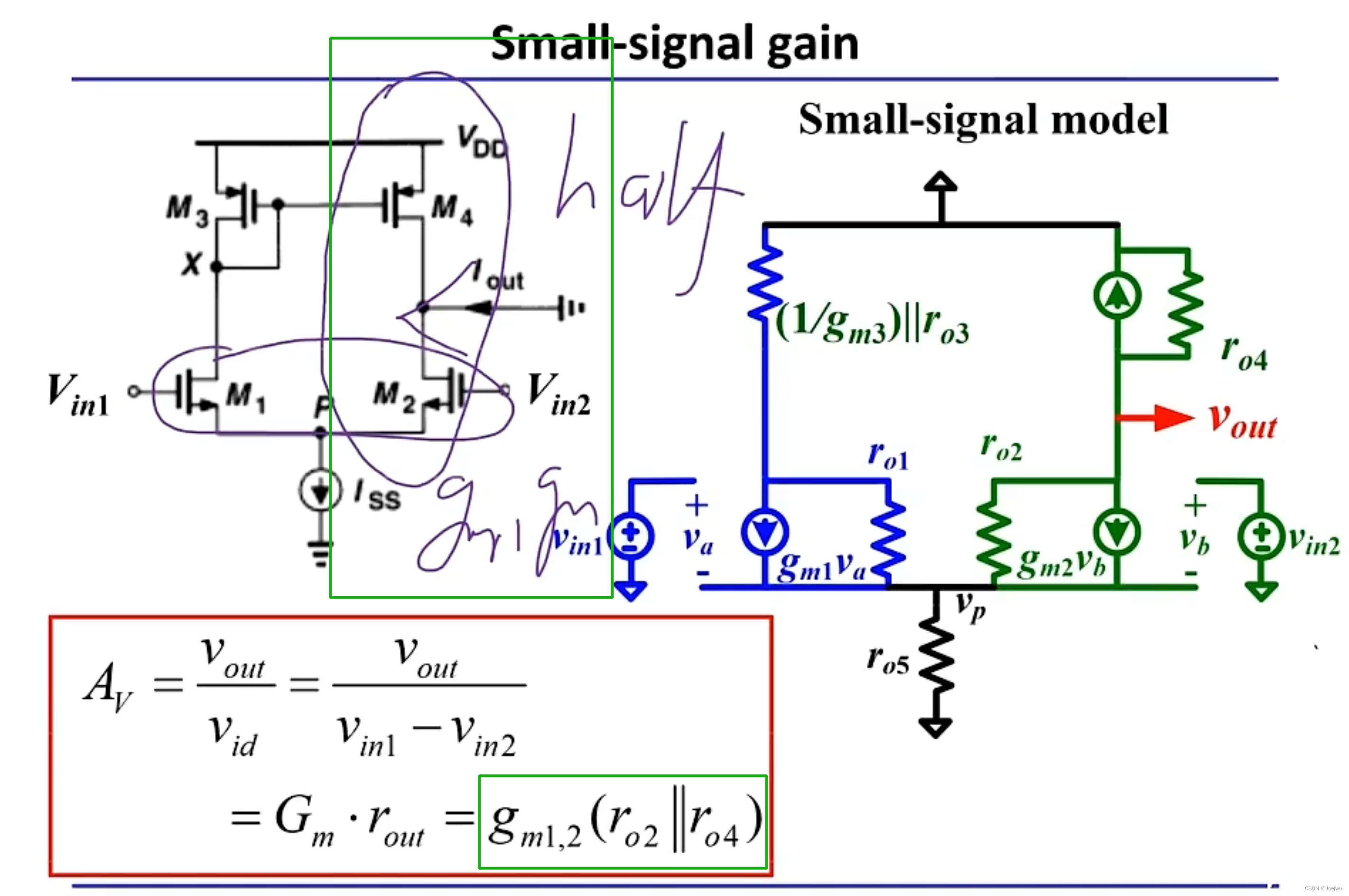
拉扎维模拟CMOS集成电路设计西交张鸿老师课程P10~13视频学习记录
--------------------------------------------------------------------------------------------------------------------------------- p10 短沟道,除了沟长调,还可能出现速度饱和问题; 但是在拉扎维这本书里面没有考虑这个问题&#…...

3.线性神经网络
#pic_center R 1 R_1 R1 R 2 R^2 R2 目录 知识框架No.1 线性回归基础优化算法一、线性回归1、买房案例2、买房模型简化3、线性模型4、神经网络5、损失函数6、训练数据7、参数学习8、显示解9、总结 二、 基础优化算法1、梯度下降2、学习率3、小批量随机梯度下降4、批量大小5、…...

python常用内置函数的介绍和使用
Python具有丰富的内置函数,这些函数是Python语言提供的基础功能。以下是一些常用的内置函数的介绍和使用: print(): 打印输出指定的内容到屏幕。 print("Hello, World!") len(): 返回给定对象的长度或元素个数。 s "Hello, World!"…...

2023辽宁省赛E
Solution 题目大致分为三个步骤 计算 P ( S ) P(S) P(S)证明删除区间连续且找到最值位置根据最值位置求出答案 接下来过程中不合法的组合数都默认为 0 0 0 第 1 步 - 求出总值 考虑 S m { 1 , 2 , ⋯ , m } S_m \{1, 2, \cdots, m\} Sm{1,2,⋯,m} , 则有 $P(S_{n2}…...

visual studio 启用C++11
用C11取决于你所使用的编译器和开发环境。以下是一些常见的编译器和相应的启用C11的方法: GCC (GNU Compiler Collection): 对于 GCC,你可以在编译时使用 -stdc11 或更高的标志来启用C11支持。例如: g -stdc11 yourfile.cpp -o yourprogramCl…...
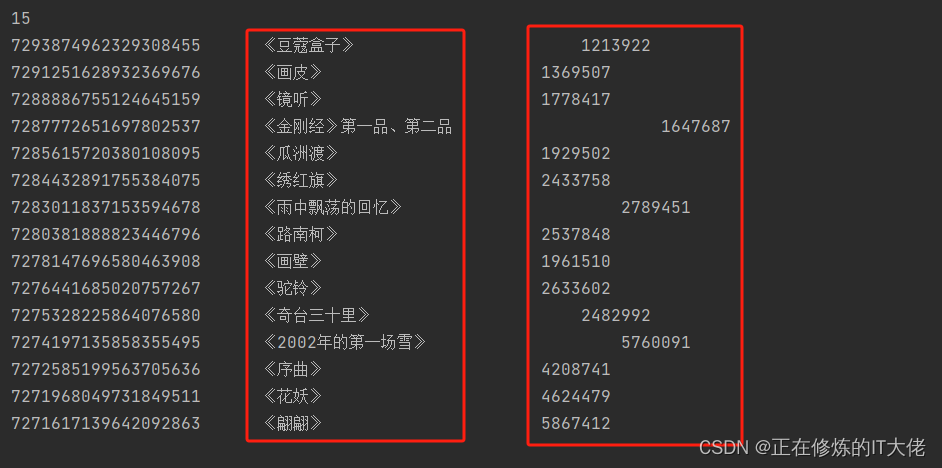
获取某个抖音用户的视频列表信息
思路 确定url确定并获取相关参数构造header发送请求解析数据输出数据 运行结果 代码 import requests # 获取某个用户的的视频信息,截至20231028,程序可以正常运行。 # 构造请求头header headers {User-Agent:..........................,Cookie:...…...
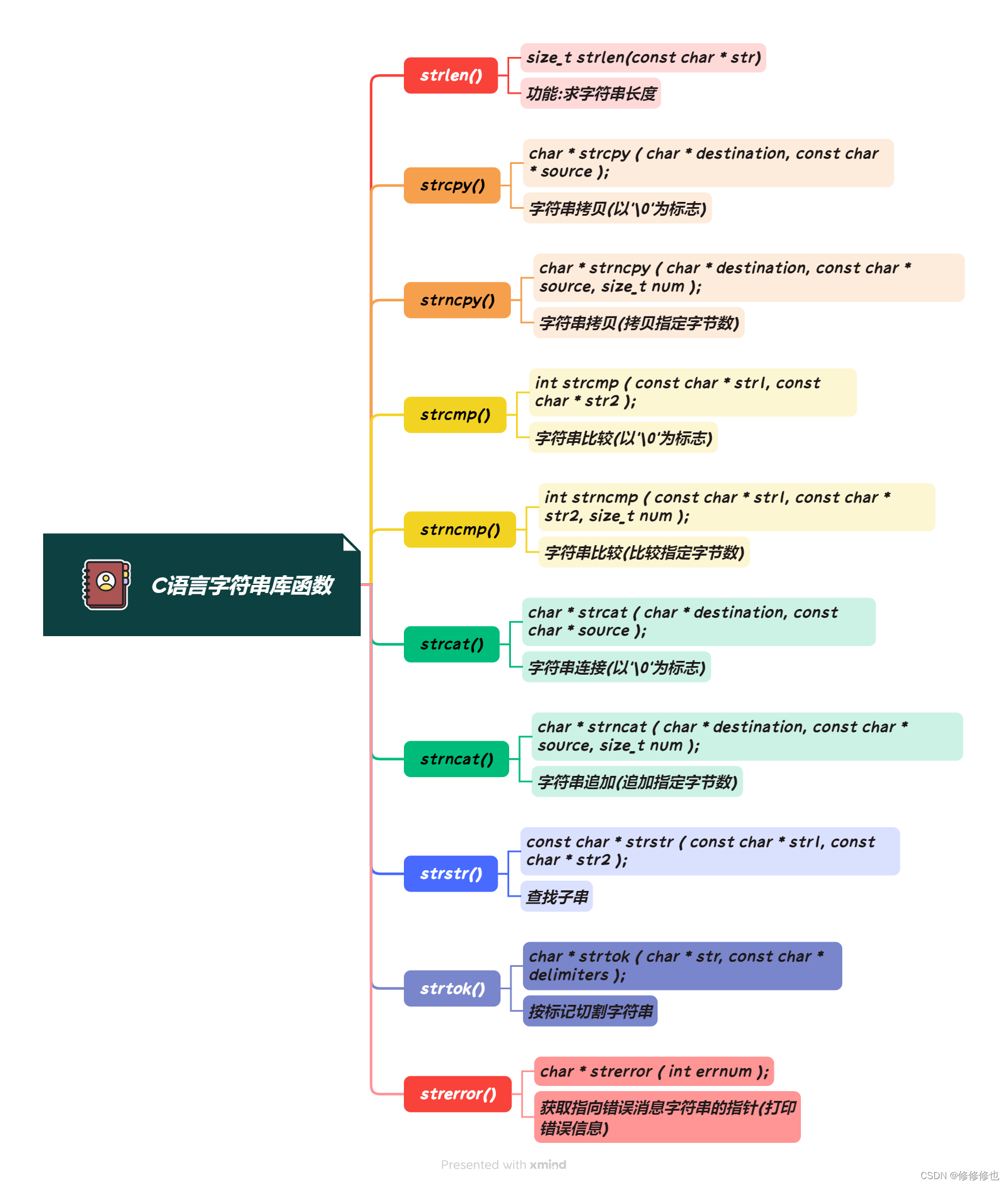
【C语言】strcpy()函数(字符串拷贝函数详解)
🦄个人主页:修修修也 🎏所属专栏:C语言 ⚙️操作环境:Visual Studio 2022 目录 一.strcpy()函数简介 1.函数功能 2.函数参数 1>.char * destination 2>.const char * source 3.函数返回值 4.函数头文件 二.strcpy()函数的具体使用 1.使用s…...

机器学习之IV编码,分箱WOE编码
IV的概念与作用 全称是Information Value,中文的意思是信息价值,或者信息量作用: 1、构建分类模型时,经常需要对特征进行筛选。 2、挑选特征的过程考虑的因素比较多,最主要和最直接的衡量标准是特征的预测能力&#…...

区块链技术与应用 【全国职业院校技能大赛国赛题目解析】第六套区块链系统部署与运维
第六套区块链系统部署与运维题目 环境 : ubuntu20 fisco : 2.8.0 子任务1-2-1: 搭建区块链系统并验证 题意: P2P起始端口 30500 channel起始端口 20500 JSONRPC 8945 使用Docker配置 使用 build_chain.sh 文件 进行生成节点文件 root@192-168-19-133:/yijiu/mode6# bas…...
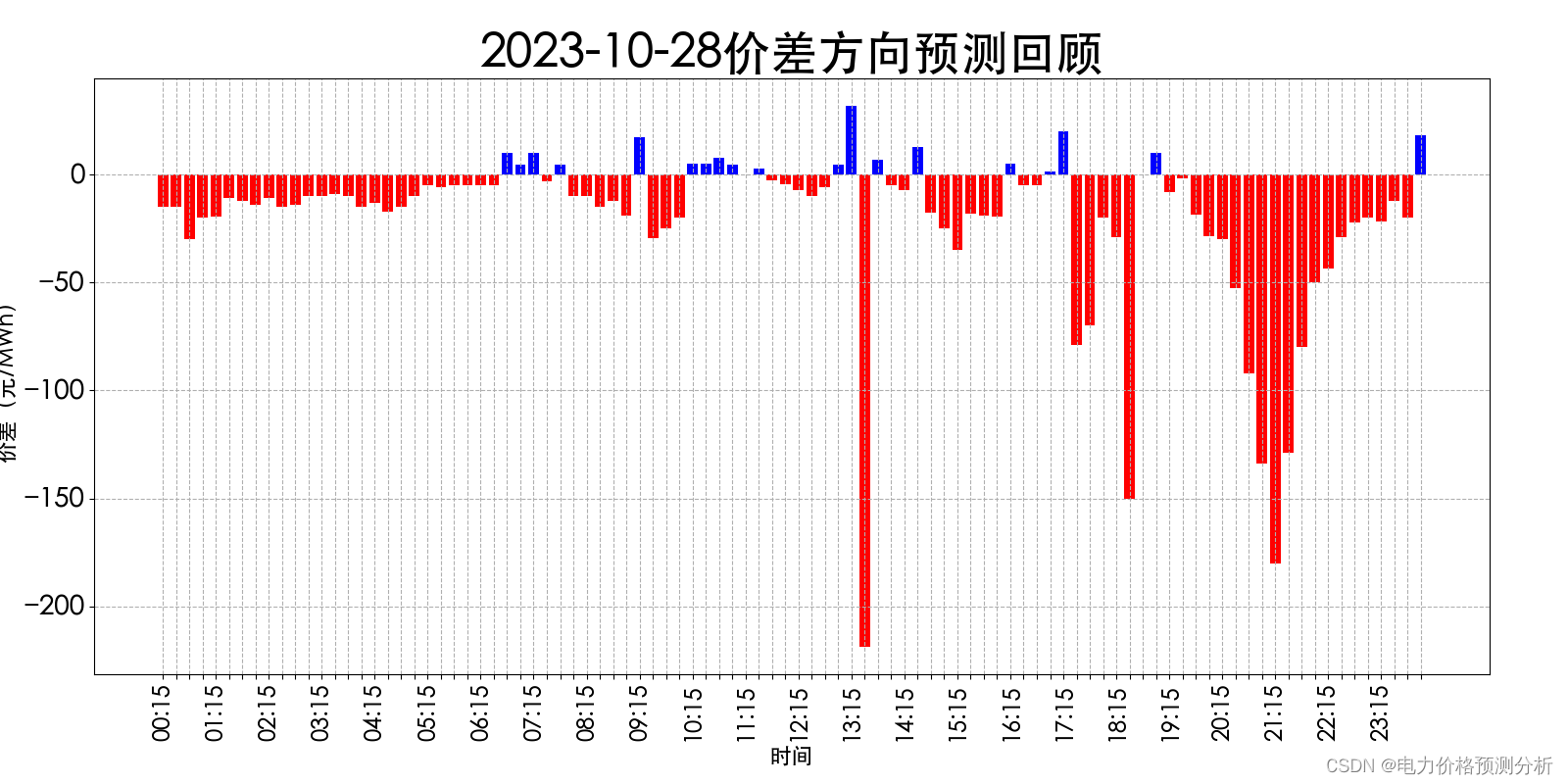
山西电力市场日前价格预测【2023-10-30】
日前价格预测 预测说明: 如上图所示,预测明日(2023-10-30)山西电力市场全天平均日前电价为309.35元/MWh。其中,最高日前电价为400.33元/MWh,预计出现在18:15。最低日前电价为0.00元/MWh,预计出…...
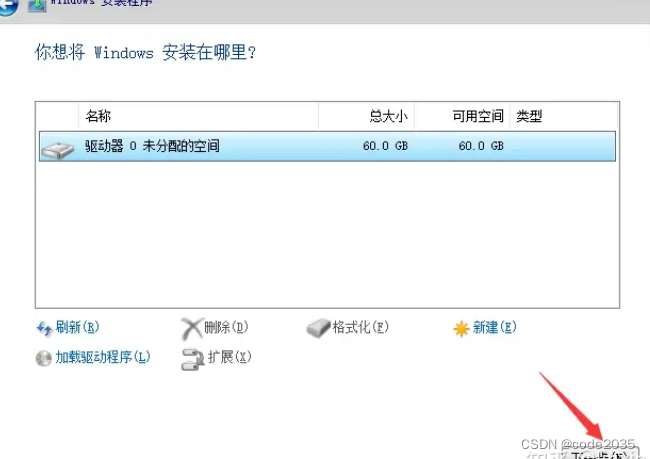
win10虚拟机安装教程
目录 1、安装VMware 10、12、16都可以,看个人选择 2、开始安装系统(以vm16为例) 3、在虚拟机中安装win10 完成 1、安装VMware 10、12、16都可以,看个人选择 下面链是我虚拟机安装包,需要可以下载。 YR云盘 软件安…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
