服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springboot+vue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自己以后查看和回顾;这篇博客分享如何安装jdk8和tomcat8,让我们往下看;
目录
一、让我们的服务器先安装好宝塔页面
二、通过宝塔面板安装jdk
为了让更多的铁子能够接受,这里我们采取用可视化页面进行操作,也就是宝塔这个软件【不是打广告哈,确实好用😭】;
一、让我们的服务器先安装好宝塔页面
1、搜索网址来到宝塔官网宝塔面板 - 简单好用的Linux/Windows服务器运维管理面板,点击产品里面的Linux面板
2、然后点击立即免费安装

3、点击在线安装

4、会跳转到一个表单页面,输入自己ip的信息
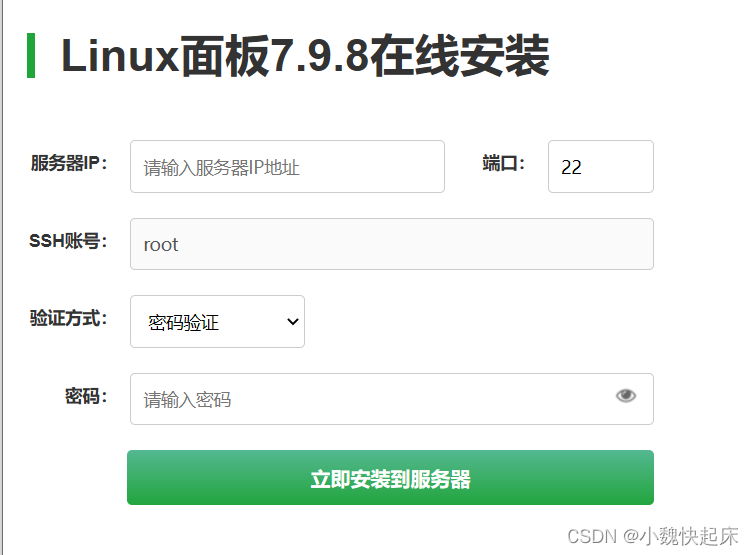
5、填写完成后,就有一个推荐套件【就是推荐你安装这些软件,比如mysql、Nginx这些后面都会用到,其他的可以不用安装,这两个留着,然后立即安装就行】
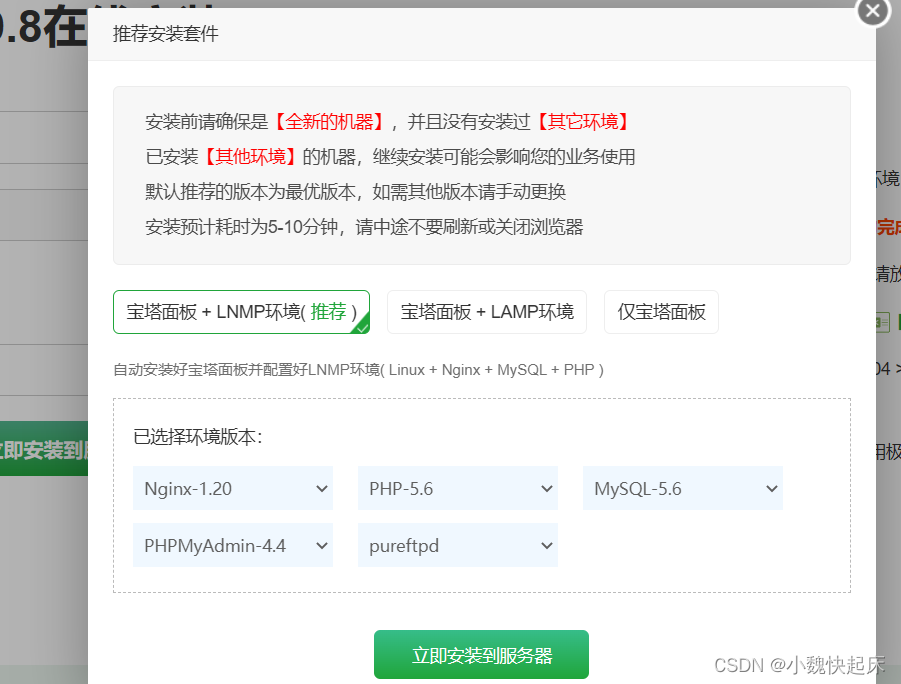
6、等待安装完成【整个过程还是要几分钟】
7、安装完成,会出现如图,这信息是登录宝塔面板用的,一定要保存好,到这里宝塔面板就安装好了;
二、通过宝塔面板安装jdk
1、登录刚刚的面板网址:例如我的是:http://112.1.1.2:8888/2a064073;
2、登录成功后,如果需要绑定手机号,直接用自己的绑定就行了,就到了我们的宝塔面板;
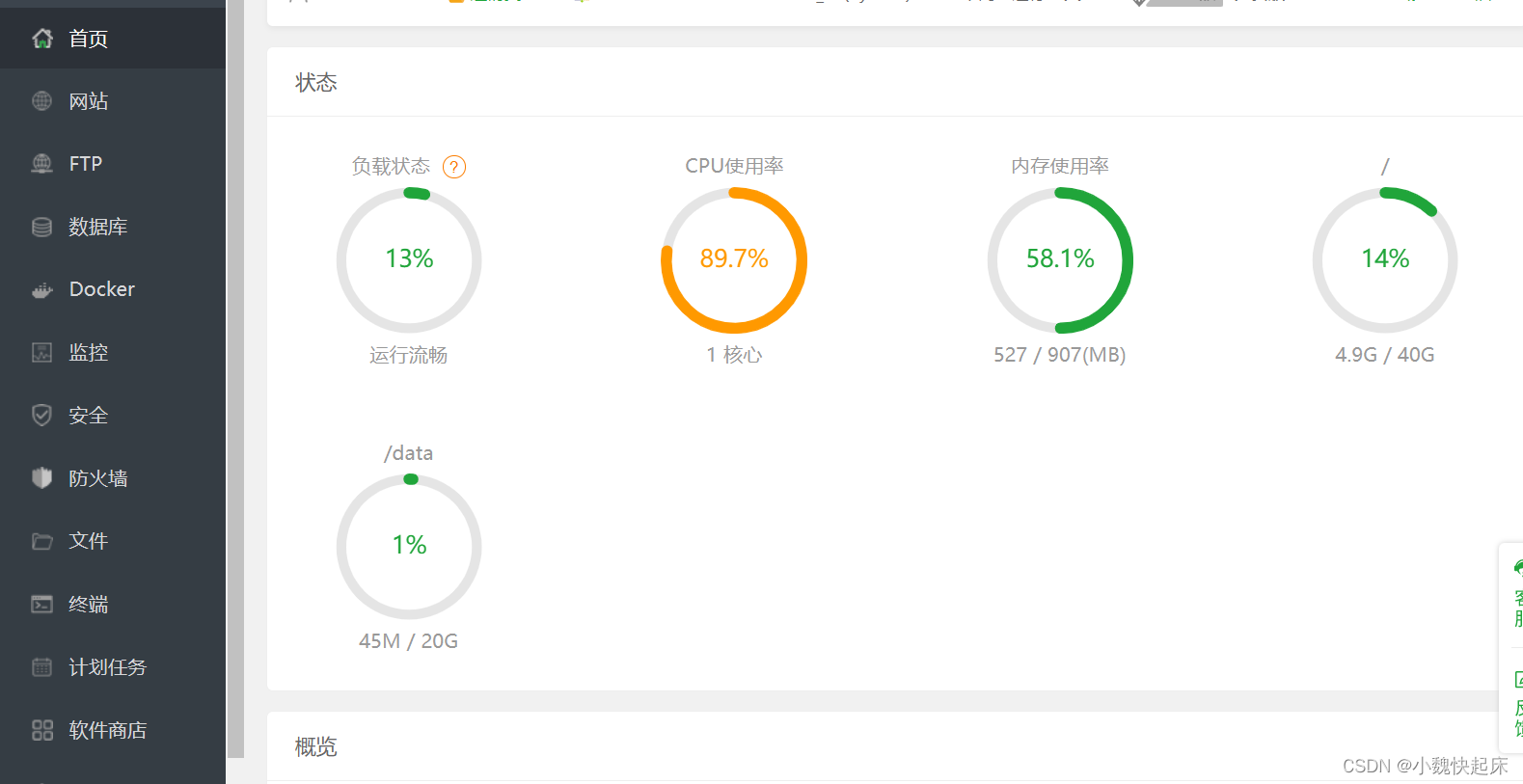
3、如下,让宝塔来安装jdk和tomcat,我们需要先安装一个工具,他来替我们安装
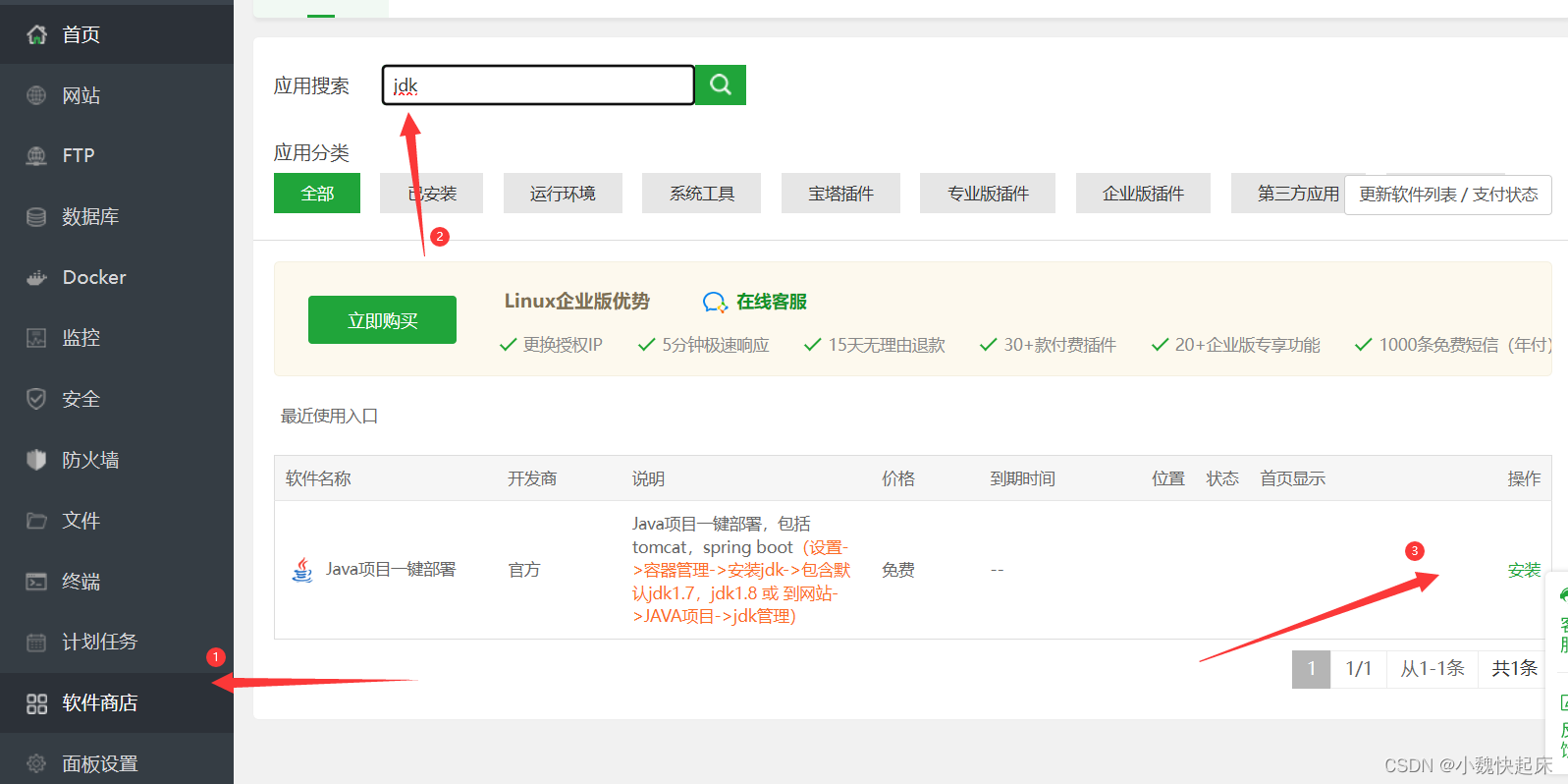

4、然后在容器管理中,我这儿选择tomcat8进行安装,然后等待完成即可
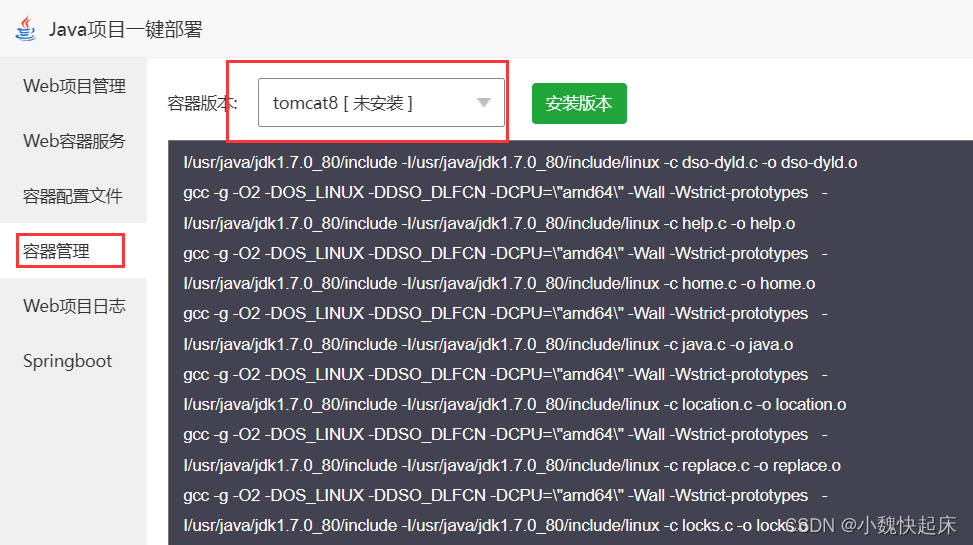
5、完成之后在ssh工具,命令行里面输入java -version即可

打完收工,看都看到这里了,更新不易,希望大家多多支持;
相关文章:

服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springbootvue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自…...

golang项目----家庭收支记账软件
家庭收支记账软件实现基本功能(先使用面向过程,后面改成面向对象)项目代码实现改进面向过程源码面向对象源码utils包中main包中实现基本功能(先使用面向过程,后面改成面向对象) 编写文件TestMyAccount.go完成基本功能 功能一:先完成可以显示…...

中国LNG市场投资机会研究
中国LNG市场投资机会研究中国LNG市场是一个具有巨大潜力和发展机遇的市场,尤其是在政府大力推动清洁能源发展的背景下,LNG市场投资机会正在不断扩大。首先,政府大力支持LNG市场的发展。政府实施的“十三五”规划将LNG作为清洁能源的重要来源&…...
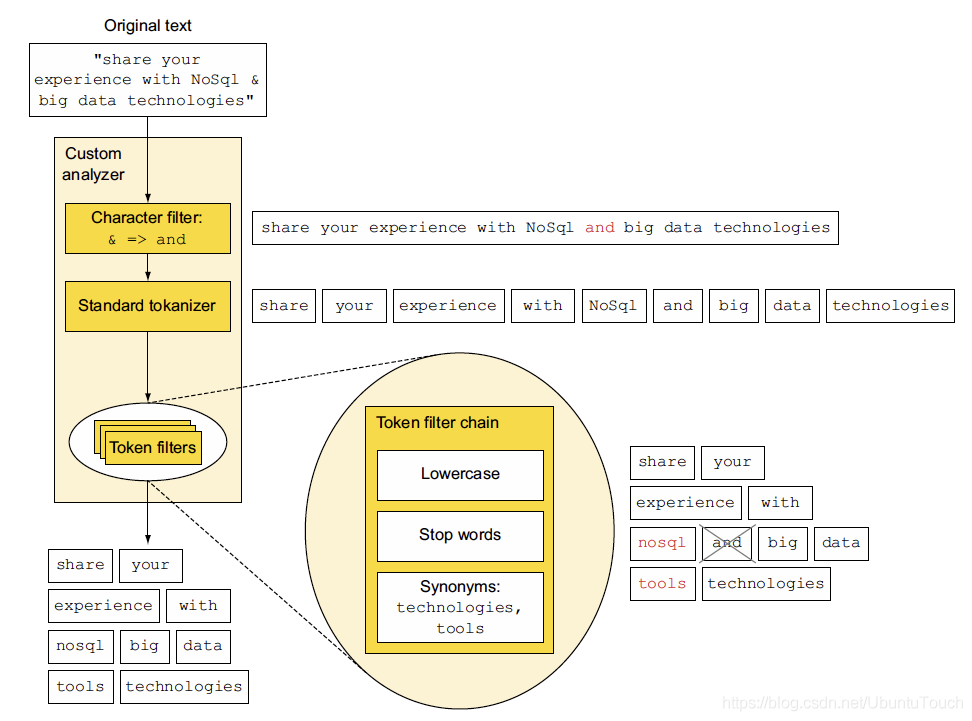
Elasticsearch:索引数据是如何完成的
在我在之前的文章 “Elasticsearch:彻底理解 Elasticsearch 数据操作” 文章中,我详细地描述了如何索引数据到 Elasticsearch 中。在今天的文章中,我想更进一步来描述这个流程。 Elasticsearch 是一个非常强大和灵活的分布式数据系统&#x…...

处理器管理
处理器状态处理器管理是操作系统中重要组成部分,负责管理、调度和分配计算机系统的重要资源——处理器,并控制程序执行由于处理器管理是操作系统最核心的部分,无论是应用程序还是系统程序,最终都要在处理器上执行以实现其功能&…...
第五)
跟着我从零开始入门FPGA(一周入门系列)第五
5、同步和异步设计 前面已有铺垫,同步就是与时钟同步。 同步就是走正步,一二一,该迈哪个脚就迈那个脚,跑的快的要等着跑的慢的。 异步就是搞赛跑,各显神通,尽最大力量去跑,谁跑得快,…...

【第42天】Arrays.sort 与 Collections.sort 应用 | 整形数组与集合的排序
本文已收录于专栏🌸《Java入门一百练》🌸学习指引序、专栏前言一.sort函数二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析三、推荐专栏序、专栏前言 本专栏开启,目的…...

LeetCode第334场周赛
2023.2.26LeetCode第334场周赛 A. 左右元素和的差值 思路 前缀和后缀和 代码 class Solution { public:vector<int> leftRigthDifference(vector<int>& nums) {int n nums.size();vector<int> l(n), r(n), ans(n);for (int i 1; i < n; i )l[…...
:PatchMatchNet配置及代码主要运行流程)
基于深度学习的三维重建网络PatchMatchNet(三):PatchMatchNet配置及代码主要运行流程
目录 1.PatchMatchNet环境配置 2. PatchMatchNet的大致执行流程(eval.py) 2.1 深度图的保存...

【一天一门编程语言】设计一门编程语言,给出基础语法代码示例,SDK设计。
文章目录设计一门编程语言,给出基础语法代码示例,SDK设计。一、编程语言设计1.1 语言名称1.2 数据类型1.3 基本运算符1.4 控制语句二、SDK设计2.1 基础库2.2 第三方库三、例子用 Mango 这门语言实现斐波那契数列。基础语法代码示例SDK 设计使用 Mango 语…...

ubuntu 下 python 安装 venv
ubuntu 下 python 安装 venv1.首先,确保您的系统已安装 Python3 和 pip3,如果没有安装,可以使用以下命令安装:2. 接着,安装 virtualenv 包,使用以下命令:3.创建 Python 虚拟环境,使用…...

HTML#1快速入门
一. 简介HTML是一门语言, 所有的网页都是用HTML编写的HTML(Hyper Text Markup Language): 超文本(超越了文本限制,除了文字信息还可以定义图片,音频,视频等)标记语言(有标签构成的语言)W3C标准: 网页主要由三部分组成(1) 结构: HTML(2) 表现: CSS(3) 行为: JavaScript二. 快速入…...
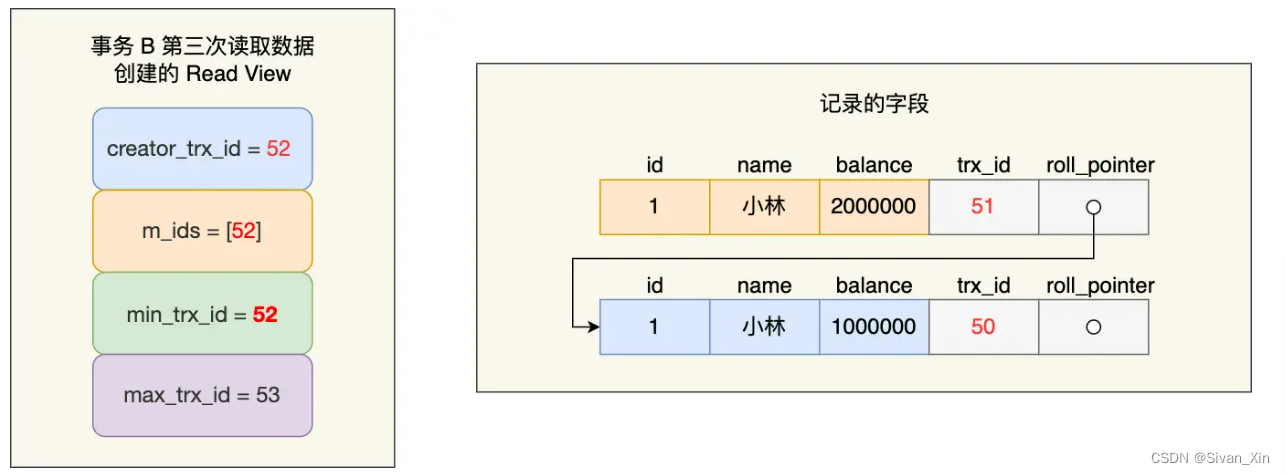
【MySQL】事务隔离级别是怎么实现的?
事务隔离级别是怎么实现的? 四种隔离级别具体的实现方式 对于「读未提交」:直接读取最新的数据就好。对于「串行化」:通过加读写锁的方式来避免并行访问。对于「读提交」和「可重复读」:通过 Read View 来实现,主要区…...
JSP网上书店系统用myeclipse定制开发mysql数据库B/S模式java编程计算机网页
一、源码特点 JSP 网上书店系统 是一套完善的系统源码,对理解JSP java 编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。研究的基本内容是基于网上书店系 统,使用JSP作为页面开发工具。Web服务的运…...

配置 Haproxy 负载均衡群集
配置 haproxy 负载均衡群集 🏆荣誉认证:51CTO博客专家博主、TOP红人、明日之星;阿里云开发者社区专家博主、技术博主、星级博主。 💻微信公众号:微笑的段嘉许 📌本文由微笑的段嘉许原创! &#…...
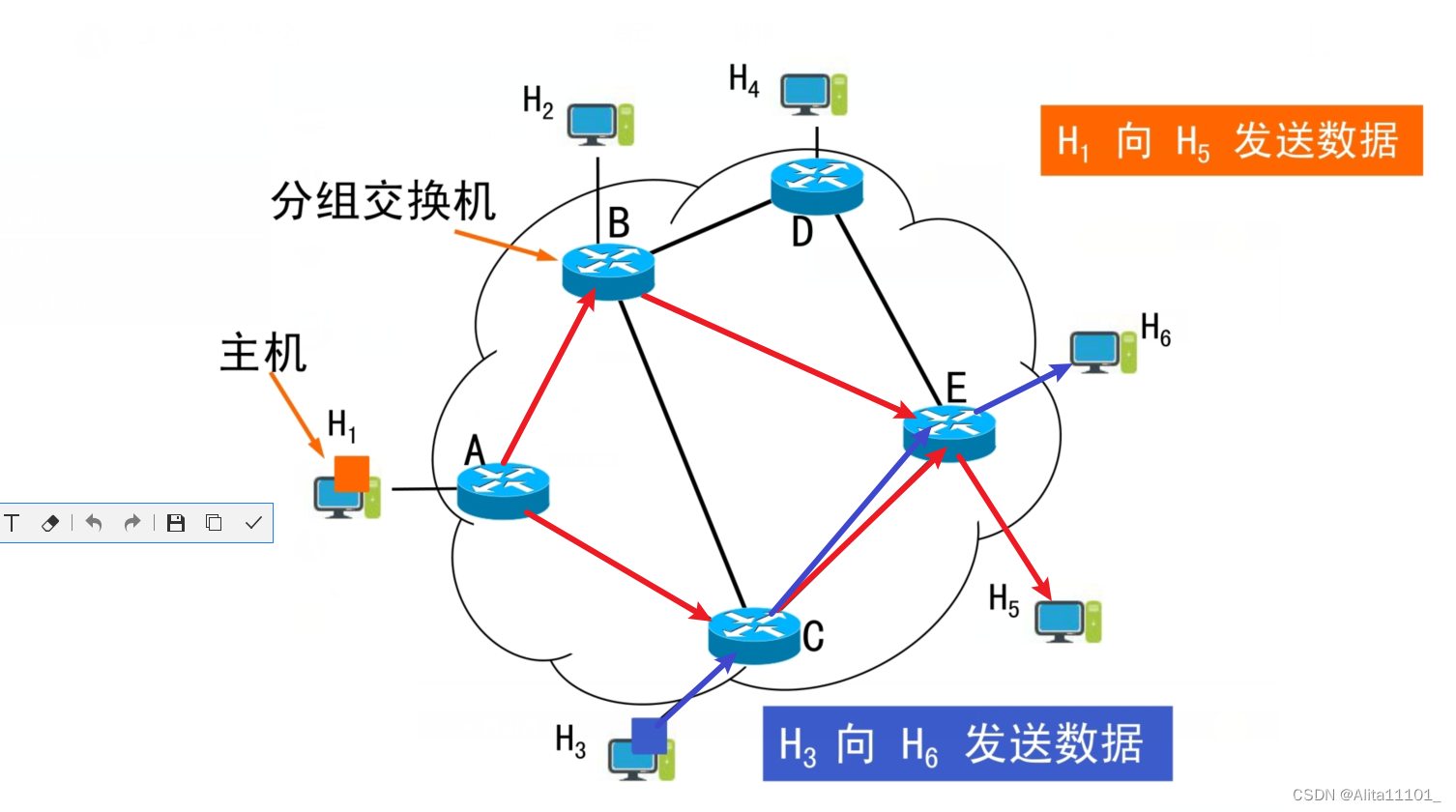
计算机网络笔记 | 第一章:计算机网络概述(1.1-1.4小节知识点整理)
从专栏将讲述有关于计算机网络相关知识点,如果有想学习Java的小伙伴可以点击下方连接查看专栏,还有JavaEE部分 本专栏地址(持续更新中):🔥计算机网络 MyBatis:✍️MyBatis Java入门篇࿱…...

Flutter3引用原生播放器-Android篇
接上篇:Flutter3引用原生播放器-IOS(Swift)篇 安卓端原生播放器的接入思路与ios基本一致,所以本篇就不废话了,直接上代码: 创建插件VideoViewPlugin实现FlutterPlugin: package io.flutter.plugins.videoplayer;imp…...
SerenityOS 操作系统类 Unix 操作系统
创建于2018年的SerenityOS是一个类似Unix的操作系统,但是带有图形化界面,适合X86台式计算机,,其界面类似90 年代的Win98/NT。几乎由一个人完成额操作系统。这几天其Web浏览器通过了 Acid3 浏览器。 Kernel features 具有抢占式多…...
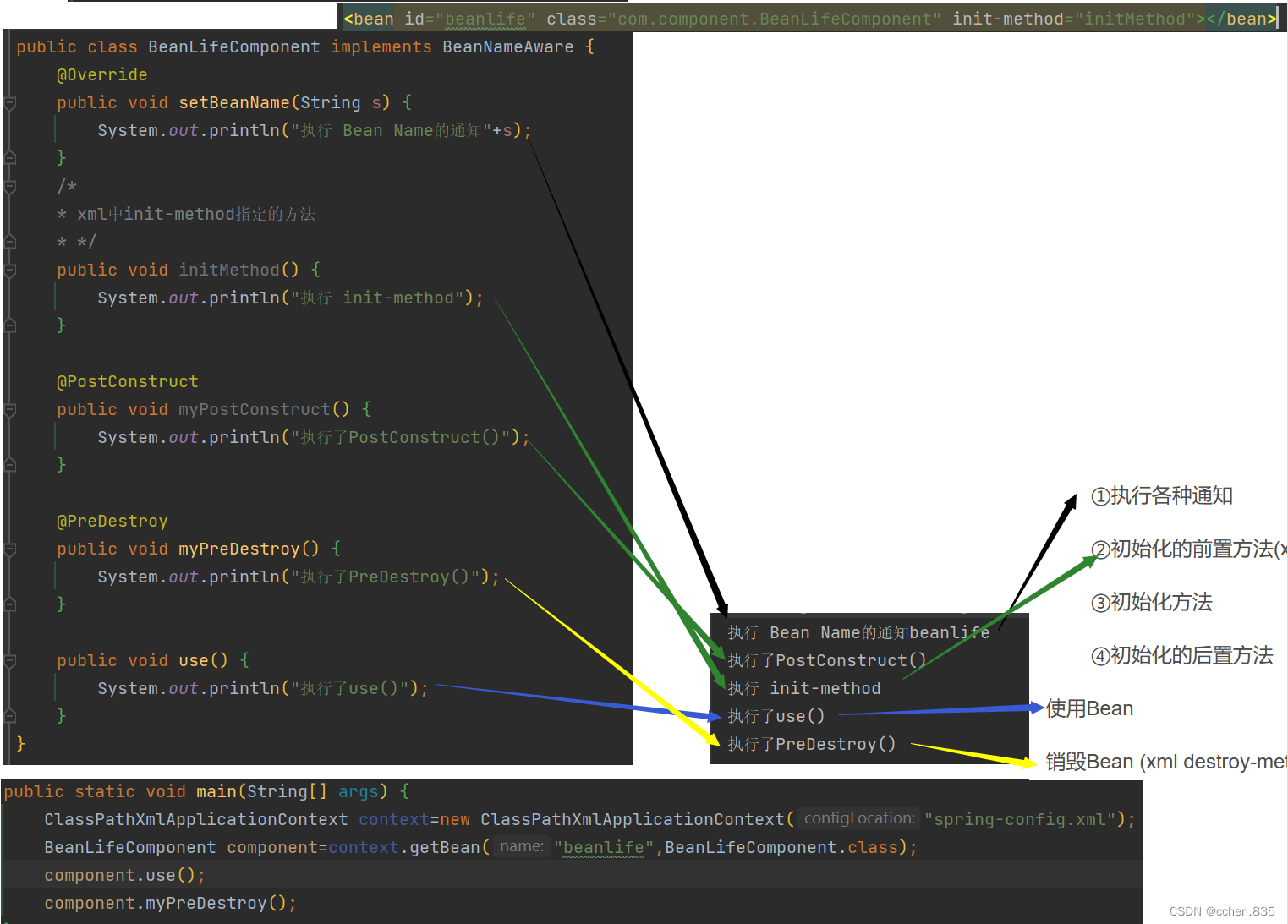
Bean作用域和生命周期
目录 Bean作用域的例子 作用域定义 Bean的六种作用域 设置作用域 Spring的执行过程和Bean的生命周期 Spring的主要执行流程 Bean的生命周期 在上篇博客中我们使用Spring存储和获取Bean,因此Bean是Spring中最重要的资源,今天这篇博客就深入了解Bean对象 Bean作用域的例子 …...
STM32笔记
目录 1.1. 预备阶段 1.2. 单片机介绍 2. 初识STM32 2.1. STM32 1.1. 预备阶段 1.2. 单片机介绍 1.2.1. 单片机是什么 单片微型计算机(Single Chip Microcomputer)简称为单片机(Microcontrollers),也称为微控制单元(Microcontroller Uni…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
