折半搜索(meet in the middle)
介绍
折半搜索,又称 meet in the middle \text{meet in the middle} meet in the middle,指将整个搜索过程分为两部分,并对两部分分别进行搜索,最后得到两个答案序列,将这两个答案序列进行合并,即可得到最终的答案。
这样做的目的是降低时间复杂度。举个例子,如果每层搜索都有两种选择,那么时间复杂度是 O ( 2 n ) O(2^n) O(2n)的。如果我们用折半搜索,那时间复杂度就降为 O ( 2 n / 2 + k ) O(2^{n/2}+k) O(2n/2+k),其中 k k k指将两个答案序列合并的时间复杂度。
例题
洛谷P4799 [CEOI2015 Day2] 世界冰球锦标赛
题目大意
有 n n n场比赛,第 i i i场比赛的门票的价格为 a i a_i ai。 Bobek \text{Bobek} Bobek有 m m m元钱,问他有多少种不同的观赛方案。
1 ≤ n ≤ 40 , 1 ≤ m ≤ 1 0 18 , 1 ≤ a i ≤ 1 0 16 1\leq n\leq 40,1\leq m\leq 10^{18},1\leq a_i\leq 10^{16} 1≤n≤40,1≤m≤1018,1≤ai≤1016
题解
我们首先可以想到的是用状压枚举每一种情况,但这样的时间复杂度为 O ( 2 n ) O(2^n) O(2n),会 TLE \text{TLE} TLE。
我们考虑用折半搜索解决问题。
先将所有比赛分为两部分,分别求出两个部分中所有可能的观赛方案的花费。那么,我们在前一部分中取方案 a a a,后一部分中取方案 b b b,则只有满足方案 a a a和方案 b b b的花费之和小于等于 m m m,这两种方案才会对答产生贡献。
那么,我们用一个数组 w w w记录前一部分的每种方案的花费,然后将 w w w从小到大排序。对于后一部分的每种方案的花费 t t t,我们在 w w w中二分求所有满足花费小于等于 m − t m-t m−t的观赛方案数量,再将其贡献在答案中即可。
求出 w w w并排序的时间复杂度为 O ( n 2 n / 2 ) O(n2^{n/2}) O(n2n/2),求出每个 t t t并二分查找的时间复杂度为 O ( n 2 n / 2 ) O(n2^{n/2}) O(n2n/2),所以总时间复杂度为 O ( n 2 n / 2 ) O(n2^{n/2}) O(n2n/2)。
code
#include<bits/stdc++.h>
using namespace std;
int n,w1=0;
long long m,now,ans=0,a[45],w[1<<20];
int main()
{scanf("%d%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}for(int s=0;s<1<<(n/2);s++){w[++w1]=0;for(int i=1;i<=n/2;i++){if((s>>i-1)&1) w[w1]+=a[i];}}sort(w+1,w+w1+1);for(int s=0;s<1<<(n-n/2);s++){now=0;for(int i=1;i<=n-n/2;i++){if((s>>i-1)&1) now+=a[n/2+i];}ans+=upper_bound(w+1,w+w1+1,m-now)-w-1;}printf("%lld",ans);return 0;
}
相关文章:
)
折半搜索(meet in the middle)
介绍 折半搜索,又称 meet in the middle \text{meet in the middle} meet in the middle,指将整个搜索过程分为两部分,并对两部分分别进行搜索,最后得到两个答案序列,将这两个答案序列进行合并,即可得到最…...
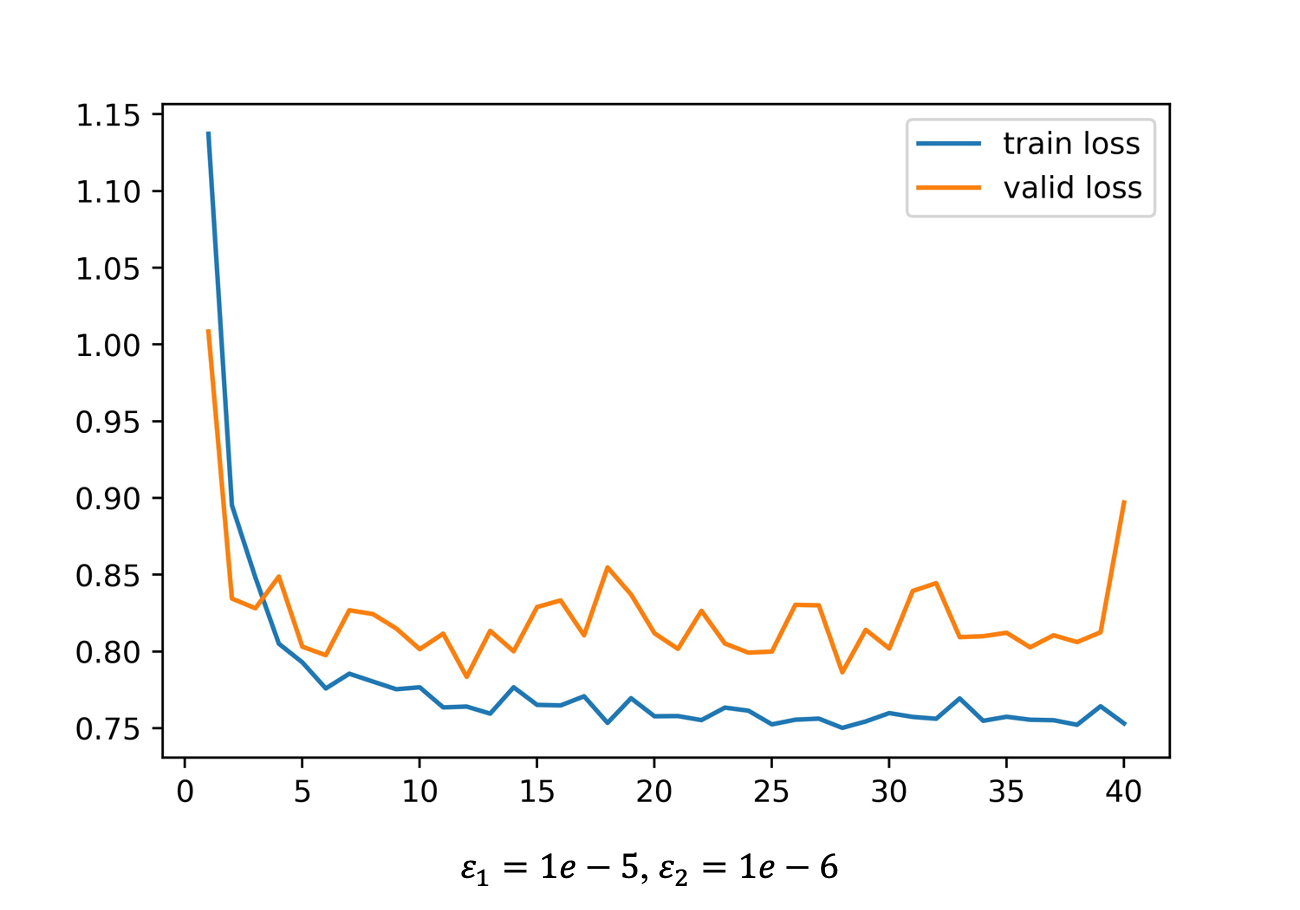
【机器学习】loss损失讨论
大纲 验证集loss上升,准确率也上升(即将overfitting?)训练集loss一定为要为0吗 Q1. 验证集loss上升,准确率也上升 随着置信度的增加,一小部分点的预测结果是错误的(log lik 给出了指数级的惩…...

LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
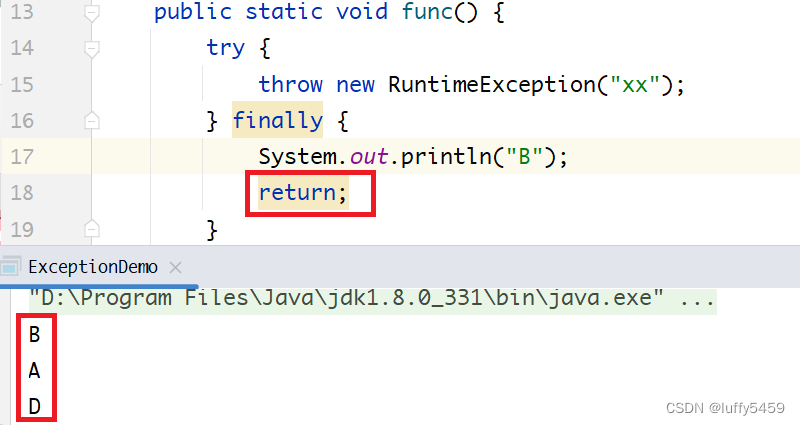
java try throw exception finally 遇上 return break continue造成异常丢失
如下所示,是一个java笔试题,考察的是抛出异常之后,程序运行结果,但是这里抛出异常,并没有捕获异常,而是通过finally来进行了流程控制处理。 package com.xxx.test;public class ExceptionFlow {public sta…...
+ Spring相关源码)
设计模式——装饰器模式(Decorator Pattern)+ Spring相关源码
文章目录 一、装饰器模式的定义二、个人理解举个抽象的例(可能并不是很贴切) 三、例子1、菜鸟教程例子1.1、定义对象1.2、定义装饰器 3、JDK源码 ——包装类4、JDK源码 —— IO、OutputStreamWriter5、Spring源码 —— BeanWrapperImpl5、SpringMVC源码 …...
MATLAB R2018b详细安装教程(附资源)
云盘链接: pan.baidu.com/s/1SsfNtlG96umfXdhaEOPT1g 提取码:1024 大小:11.77GB 安装环境:Win10/Win8/Win7 安装步骤: 1.鼠标右击【R2018b(64bit)】压缩包选择【解压到 R2018b(64bit)】 2.打开解压后的文件夹中的…...
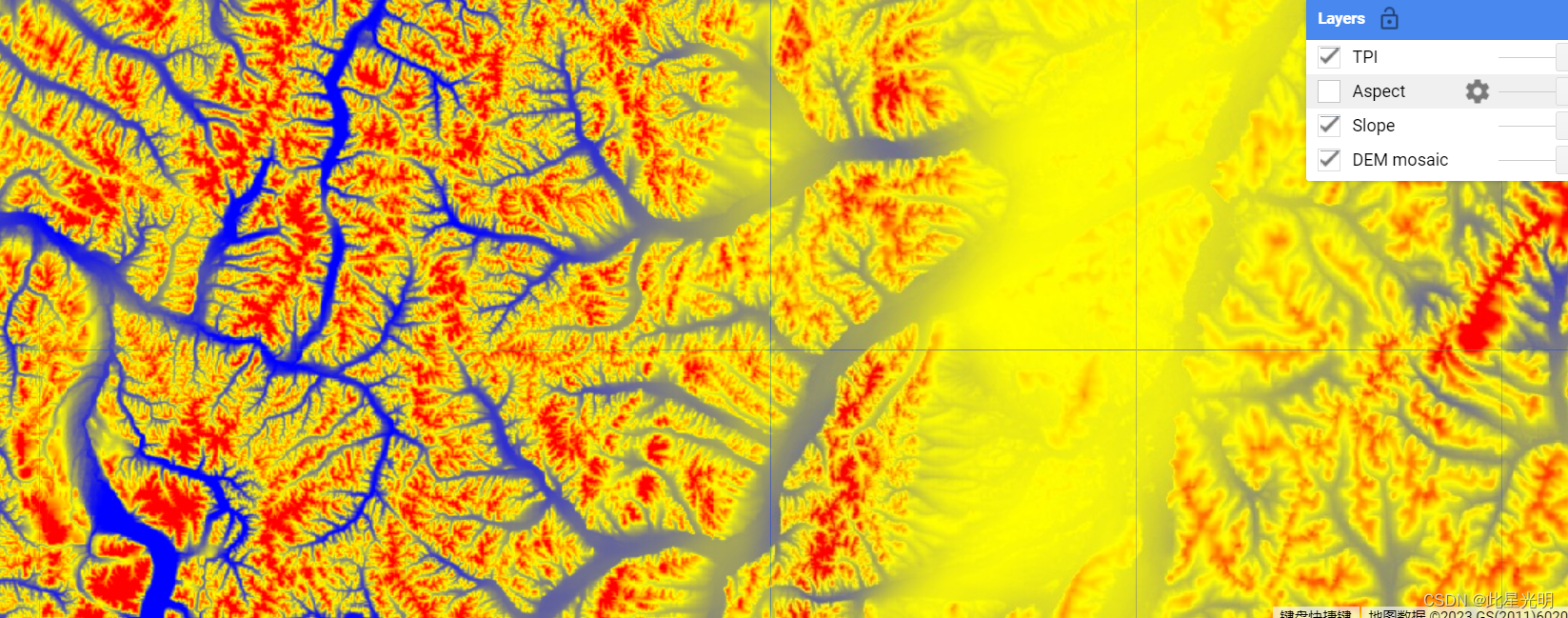
GEE错误——影像加载过程中出现的图层无法展示的解决方案
问题: // I dont know if some standard value exists for the radius, in the same, I will assume that some software would prefer to use square shape, but circle makes more sense to me. // pixels is noice if you want to zoom in and out to visualize…...
读图数据库实战笔记03_遍历
1. Gremlin Server只将数据存储在内存中 1.1. 如果停止Gremlin Server,将丢失数据库里的所有数据 2. 概念 2.1. 遍历(动词) 2.1.1. 当在图数据库中导航时,从顶点到边或从边到顶点的移动过程 2.1.2. 类似于在关系数据库中的查…...

QT如何检测当前系统是是Windows还是Uninx或Mac?以及是哪个版本?
简介 通过Qt获取当前系统及版本号,需要用到QSysInfo。 QSysInfo类提供有关系统的信息。 WordSize指定了应用程序编译所在的平台的指针大小。 ByteOrder指定了平台是大端序还是小端序。 某些常量仅在特定的平台上定义。您可以使用预处理器符号Q_OS_WIN和Q_OS_MACOS来…...
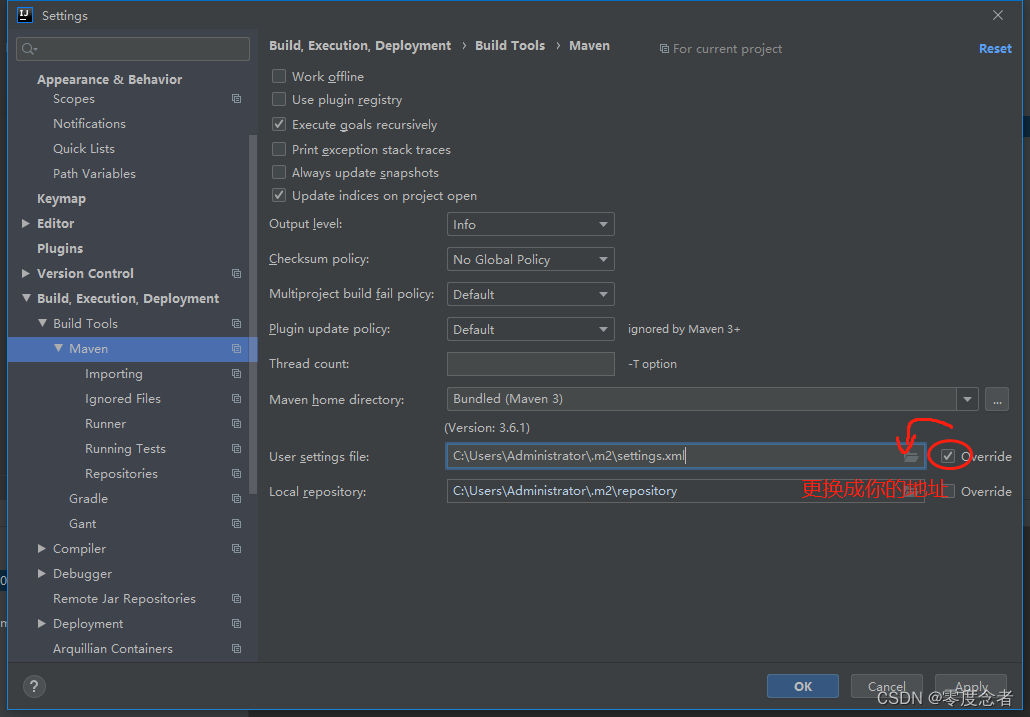
Maven配置阿里云中央仓库settings.xml
Maven配置阿里云settings.xml 前言一、阿里云settings.xml二、使用步骤1.任意目录创建settings.xml2.使用阿里云仓库 总结 前言 国内网络从maven中央仓库下载文件通常是比较慢的,所以建议配置阿里云代理镜像以提高jar包下载速度,IDEA中我们需要配置自己…...

由浅入深C系列八:如何高效使用和处理Json格式的数据
如何高效使用和处理JSON格式的数据 问题引入关于CJSON示例代码头文件引用处理数据 问题引入 最近的项目在用c处理后台的数据时,因为好多外部接口都在使用Json格式作为返回的数据结构和数据描述,如何在c中高效使用和处理Json格式的数据就成为了必须要解决…...
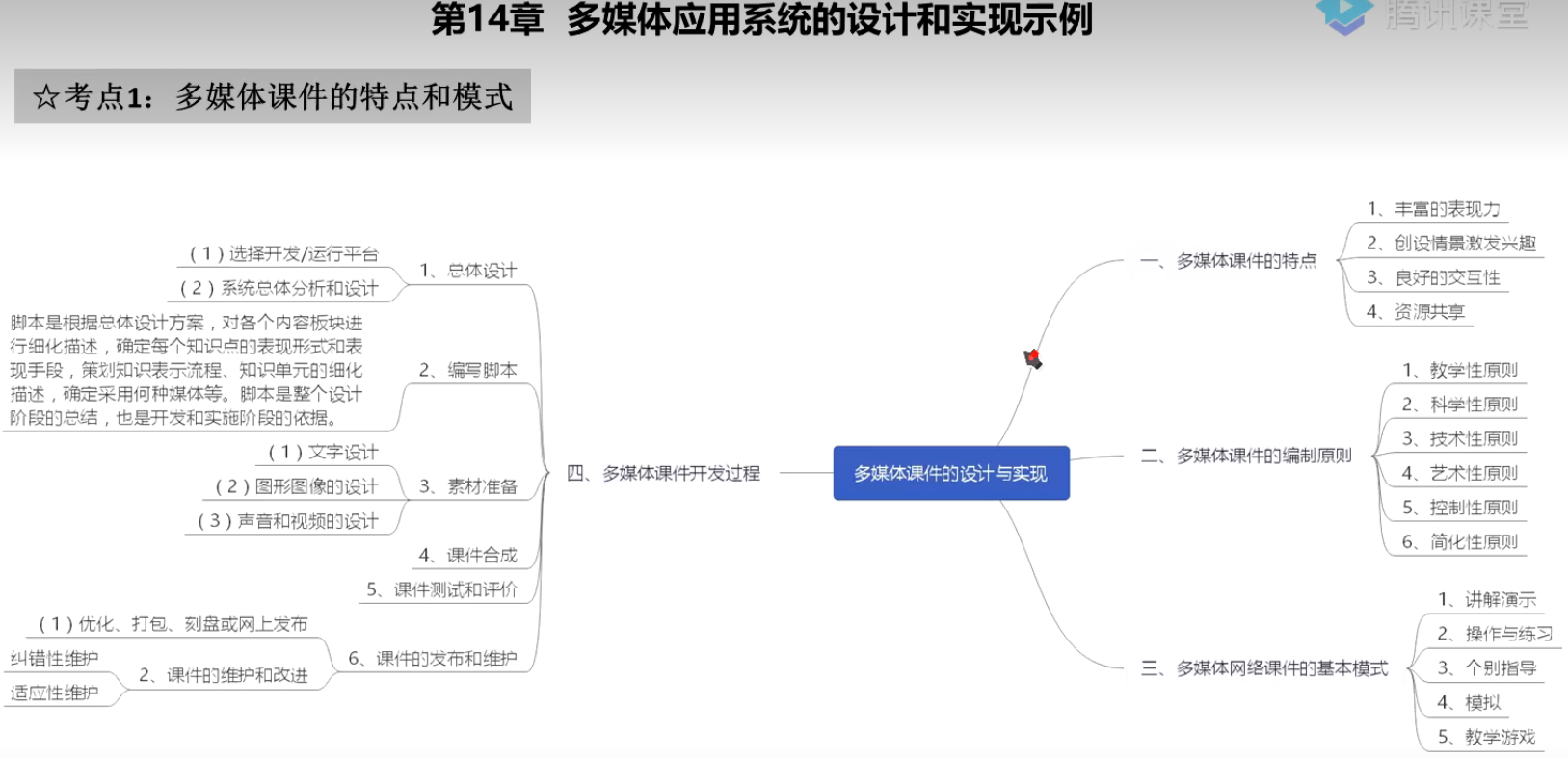
多媒体应用设计师 第16章 多媒体应用系统的设计和实现示例
口诀 思维导图 2020...

golang平滑重启库overseer实现原理
overseer主要完成了三部分功能: 1、连接的无损关闭,2、连接的平滑重启,3、文件变更的自动重启。 下面依次讲一下: 一、连接的无损关闭 golang官方的net包是不支持连接的无损关闭的,当主监听协程退出时,…...
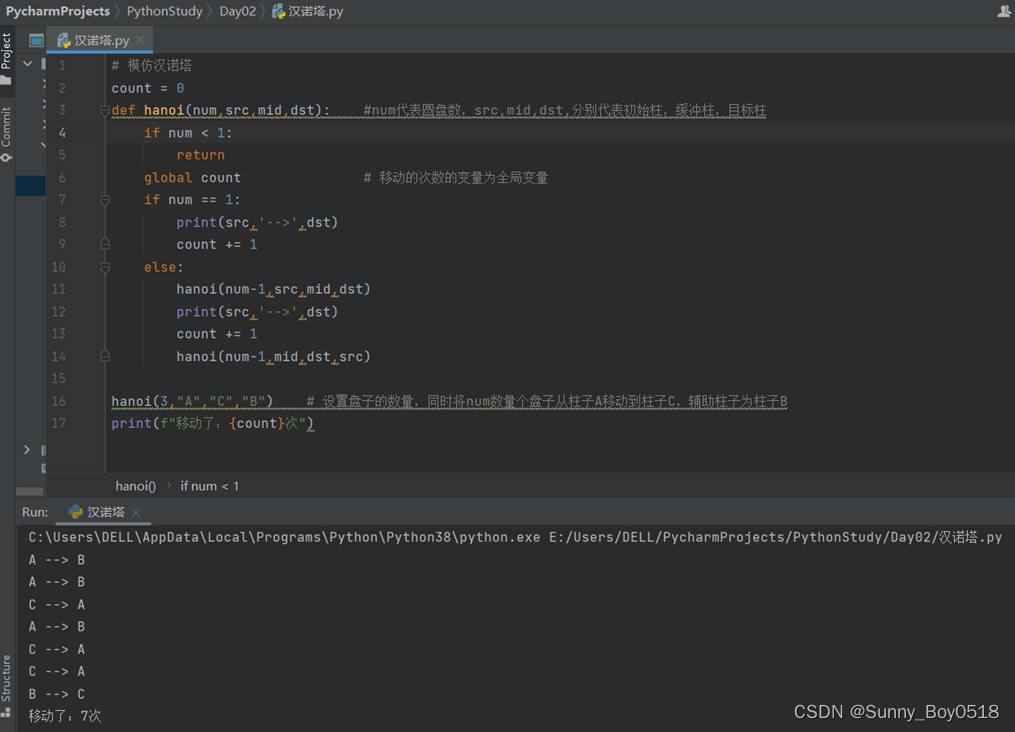
用Python定义一个函数,用递归的方式模拟汉诺塔问题
【任务需求】 定义一个函数,用递归的方式模拟汉诺塔问题,三个柱子,分别为A、B、C,其中A柱子上有N个盘子,从小到大编号为1到N,盘子大小不同。现在要将这N个盘子从A柱子移动到C柱子上,但移动的过…...

二手的需求
案例1030 某天项目经理小王,从用户现场带回了需求,以图形的方式,交给了产品经理。告诉他就照这样设计,结果是项目经理放弃让产品经理出效果图。 原因是产品经理觉得项目经理带回来的需求有问题。项目经理解释产品经理不接受&…...
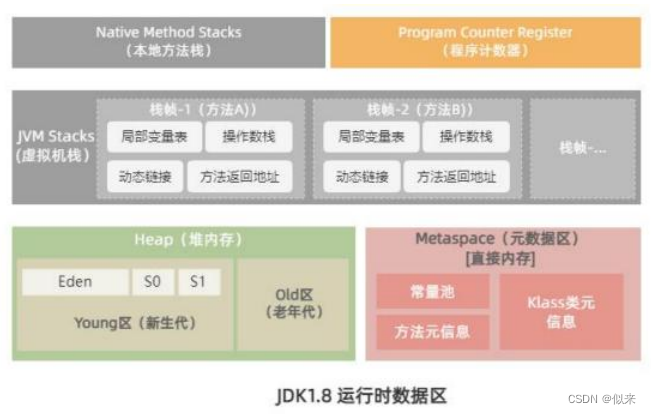
大厂面试题-JVM为什么使用元空间替换了永久代?
目录 面试解析 问题答案 面试解析 我们都知道Java8以及以后的版本中,JVM运行时数据区的结构都在慢慢调整和优化。但实际上这些变化,对于业务开发的小伙伴来说,没有任何影响。 因此我可以说,99%的人都回答不出这个问题。 但是…...
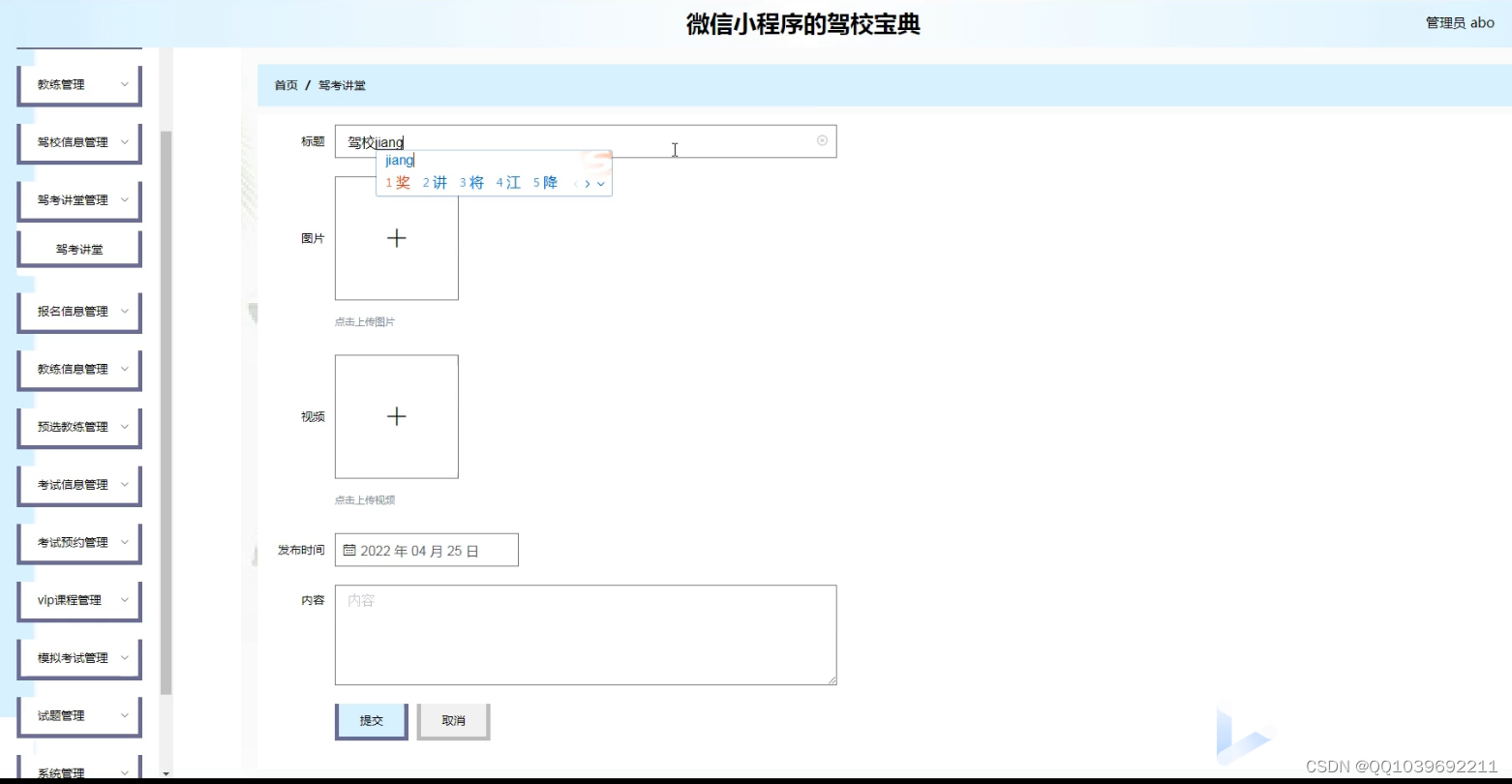
基本微信小程序的驾校宝典系统-驾照考试系统
项目介绍 系统模块分析是对系统的各个模块做出相应的说明以及解释。此系统的模块分别有用户模块、服务端模块和管理端模块这两大基本模块,其中服务端模块包括了首页、教练信息、教练咨讯、考试预约、我的等;而管理端模块则包括了个人中心、用户管理、教…...
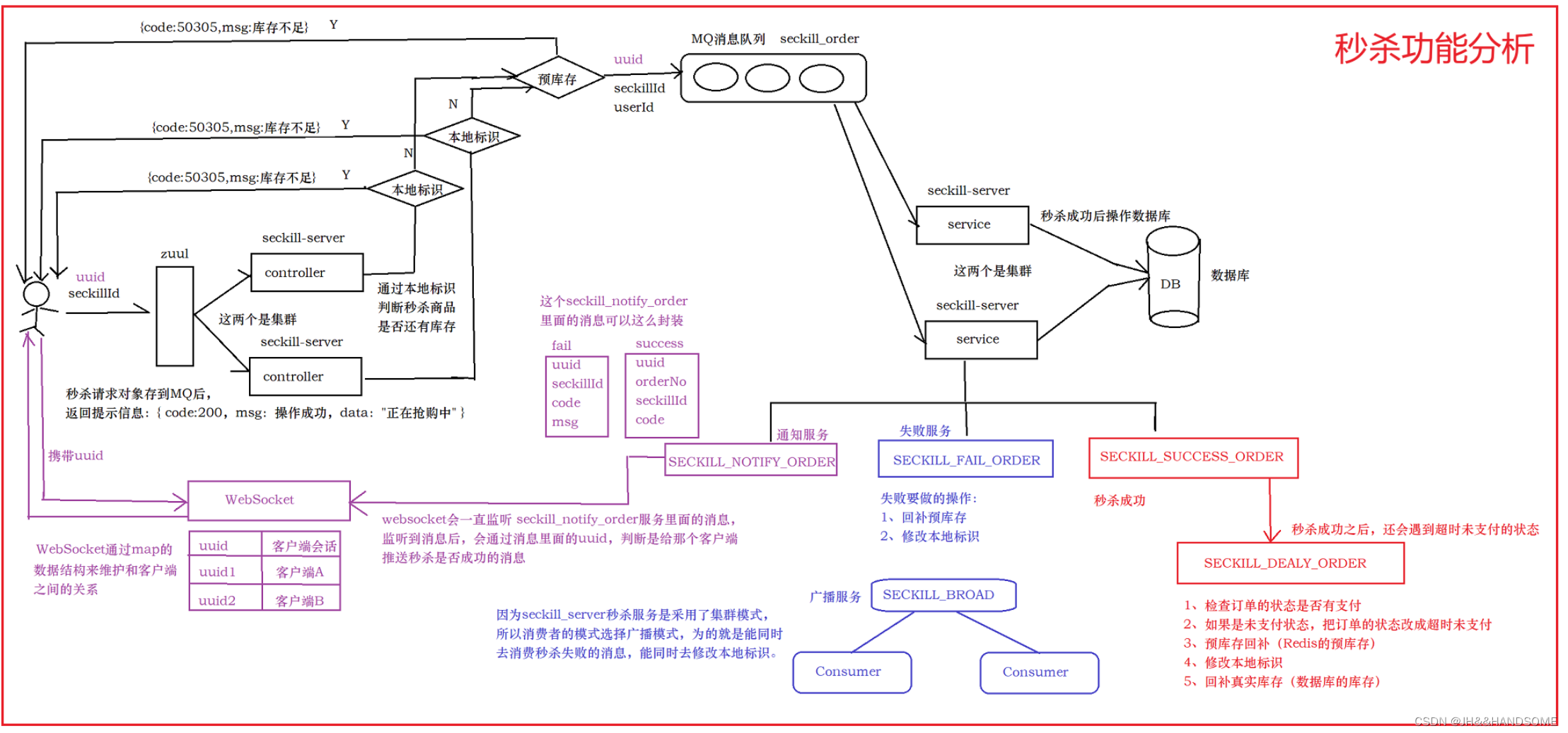
02、SpringCloud -- Redis和Cookie过期时间刷新功能
目录 需求:代码流程过滤器类工具类过滤判断远程调用feign接口gitee 配置接口实现过滤器run方法测试:问题:秒杀功能完整分析图 需求: cookie应该写在网关中,网关中可以自定义filter过滤器,用来实现cookie的刷新和redis中key的刷新,延长用户的操作时间。 就是让用户每操…...

【报错】kali安装ngrok报错解决办法(zsh: exec format error: ./ngrok)
问题描述 kali安装ngrok令牌授权失败 在安装配置文件的时候报错:zsh: exec format error: ./ngrok 原因分析: 在Kali Linux上执行./ngrok时出现zsh exec格式错误的问题可能是由于未安装正确版本的ngrok或操作系统不兼容ngrok导致的。以下是一些可能的解…...

<学习笔记>从零开始自学Python-之-常用库篇(十三)内置小型数据库shelve
一、shelve简介: shelve是Python当中数据储存的方案,类似key-value数据库,便于保存Python对象,shelve只有一个open()函数,用来打开指定的文件(字典),会返回一…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
