spting Boot常见知识点
31.介绍一下 SpringBoot，有哪些优点？
1、Spring Boot 基于 Spring 开发，Spirng Boot 本身并不提供 Spring 框架的核心特性以及扩展功能，只是用于快速、敏捷地开发新一代基于 Spring 框架的应用程序。它并不是用来替代 Spring 的解决方案，而是和 Spring 框架紧密结合用于提升 Spring 开发者体验的工具。
Spring Boot 以约定大于配置核心思想开展工作，相比 Spring 具有如下优势：
- Spring Boot 可以快速创建独立的 Spring 应用程序。
- Spring Boot 内嵌了如 Tomcat，Jetty 和 Undertow 这样的容器，也就是说可以直接跑起来，用不着再做部署工作了。
- Spring Boot 无需再像 Spring 一样使用一堆繁琐的 xml 文件配置。
- Spring Boot 可以自动配置(核心)Spring。SpringBoot 将原有的 XML 配置改为 Java 配置，将 bean 注入改为使用注解注入的方式(@Autowire)，并将多个 xml、properties 配置浓缩在一个 appliaction.yml 配置文件中。
- Spring Boot 提供了一些现有的功能，如量度工具，表单数据验证以及一些外部配置这样的一些第三方功能。
- Spring Boot 可以快速整合常用依赖（开发库，例如 spring-webmvc、jackson-json、validation-api 和 tomcat 等），提供的 POM 可以简化 Maven 的配置。当我们引入核心依赖时，SpringBoot 会自引入其他依赖。
相关文章：
spting Boot常见知识点
31.介绍一下 SpringBoot，有哪些优点？ 1、Spring Boot 基于 Spring 开发，Spirng Boot 本身并不提供 Spring 框架的核心特性以及扩展功能，只是用于快速、敏捷地开发新一代基于 Spring 框架的应用程序。它并不是用来替代 Spring 的解…...
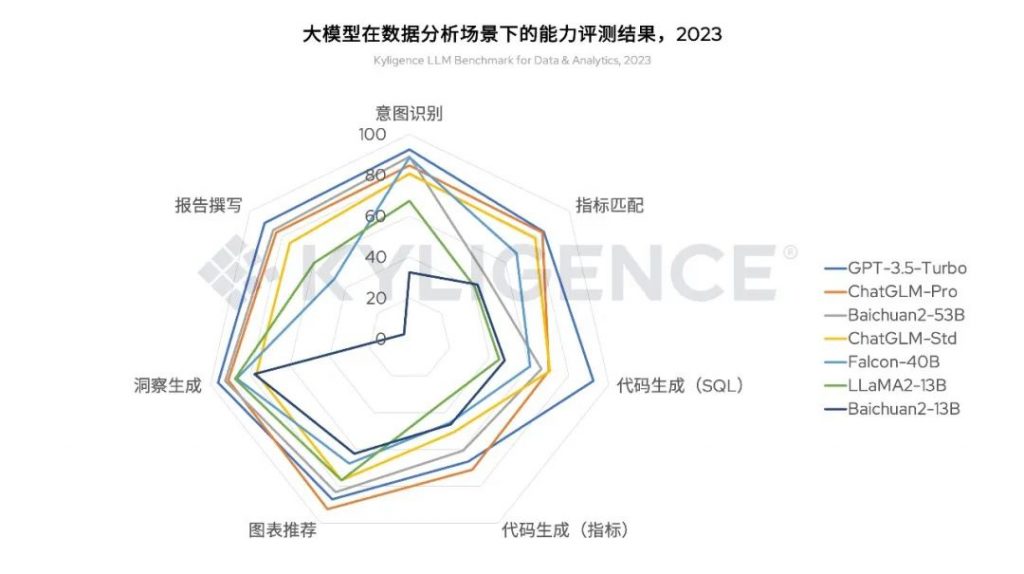
大模型在数据分析场景下的能力评测
“你们能对接国产大模型吗？” “开源的 LLaMA 能用吗，中文支持怎么样？” “私有化部署和在线服务哪个更合适？” 自 7 月 14 日发布 AI 数智助理 Kyligence Copilot 后，我们收到了很多类似上面的咨询，尤其…...
[笔记] 关于y1变量取名冲突的问题
参考博客 遇到的问题和这位老哥的一模一样。 结论是：当我们用math头文件的时候，不能在全局定义 y0 和 y1，j0、j1、jn、yn。...
js笔记（函数参数、面向对象、装饰器、高级函数、捕获异常）
JavaScript 笔记 函数参数 默认参数 在 JavaScript 中，我们可以为函数的参数设置默认值。如果调用函数时没有传递参数，那么参数将使用默认值。 function greet(name World) {console.log(Hello, ${name}!); }greet(); // 输出：Hello, Wo…...
Istio实战（八）- Istio 动态准入 Webhook 配置
准入 Webhook 是 HTTP 方式的回调，接收准入请求并对其进行相关操作。 可定义两种类型的准入 Webhook，Validating 准入 Webhook 和 Mutating 准入 Webhook。使用 Validating Webhook，可以通过自定义的准入策略来拒绝请求； 使用 Mut…...
Vue的安装
----------------------------------------------------前置---------------------------------------------------- 1.node.js的下载安装、缓存路径的设置 ①安装 ②设置npm prefix, cache 2.NODE_PATH、PATH ①系统变量中加 ②PATH中加 3.配置镜像源 -----------------------…...
macOS M1安装wxPython报错
macOS12.6.6 M1安装wxPython失败： 报错如下： imagtiff.cpp:37:14: fatal error: tiff.h file not found解决办法： 下载源文件重新编译（很快，5分钟全部搞定），分三步走： 第一步&…...
【数据结构】交换排序
⭐ 作者：小胡_不糊涂 🌱 作者主页：小胡_不糊涂的个人主页 📀 收录专栏：浅谈数据结构 💖 持续更文，关注博主少走弯路，谢谢大家支持 💖 冒泡、快速排序 1. 冒泡排序2. 快速…...
腾讯云2023年双11服务器优惠活动及价格表
腾讯云2023年双11大促活动正在火热进行中，腾讯云推出了一系列服务器优惠活动，云服务器首年1.8折起，买1年送3个月！境外云服务器15元/月起，买更多省更多！下面给大家分享腾讯云双11服务器优惠活动及价格表&…...
PointNet++复现、论文和代码研读
文章目录 复现1.创建虚拟环境并进入2.安装pytorch3.分割模型的训练和测试3.1.下载数据处理数据3.2.训练分割模型3.3分割模型的测试 4.分类模型的训练和测试 论文研读制作自己的数据集流程分割模型数据集准备 复现 https://github.com/yanx27/Pointnet_Pointnet2_pytorch 1.创…...
轨迹规划 | 图解路径跟踪PID算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 PID控制基本原理2 基于PID的路径跟踪3 仿真实现3.1 ROS C实现3.2 Python实现3.3 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)&a…...
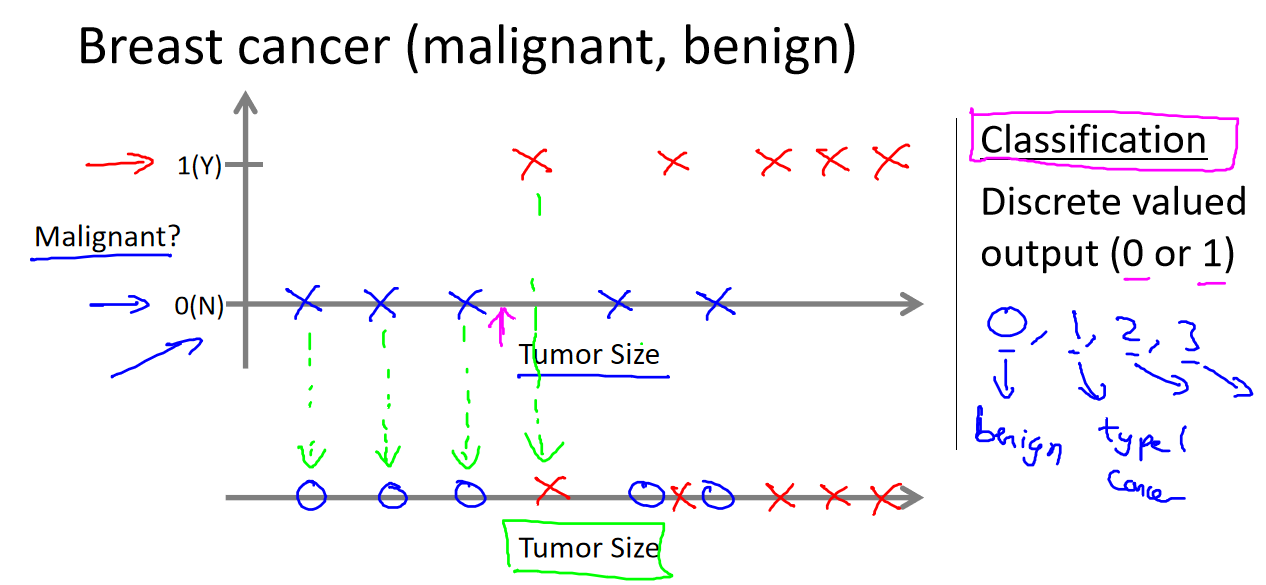
吴恩达《机器学习》1-3:监督学习
一、监督学习 例如房屋价格的数据集。在监督学习中，我们将已知的房价作为"正确答案"，并将这些价格与房屋的特征数据一起提供给学习算法。学习算法使用这些已知答案的数据来学习模式和关系，以便在未知情况下预测其他房屋的价格。这就…...
Flutter PopupMenuButton下拉菜单
下拉菜单是移动应用交互中一种常见的交互方式，可以使用下拉列表来展示多个内容标签，实现页面引导的作用。在Flutter开发中，实现下拉弹框主要有两种方式，一种是继承Dialog组件使用自定义布局的方式实现，另一种则是使用官方的PopupMenuButton组件进行实现。 如果没有特殊的…...
国家数据局正式揭牌，数据专业融合型人才迎来发展良机【文末送书五本】
国家数据局正式揭牌，数据专业融合型人才迎来发展良机 国家数据局正式揭牌，数据专业融合型人才迎来发展良机 摘要书籍简介数据要素安全流通Python数据挖掘：入门、进阶与实用案例分析数据保护：工作负载的可恢复性Data Mesh权威指南分…...
H5游戏源码分享-像素小鸟游戏（类似深海潜艇）
H5游戏源码分享-像素小鸟游戏（类似深海潜艇） 点击屏幕控制小鸟的飞行高度 整个小游戏就用JS完成 项目地址：https://download.csdn.net/download/Highning0007/88483228 <!DOCTYPE HTML> <html><head><meta http-equiv…...
Vue 3 响应式对象：ref 和 reactive 的使用和区别
🎉🎉欢迎来到我的CSDN主页！🎉🎉 🏅我是尘缘，一个在CSDN分享笔记的博主。📚📚 👉点击这里，就可以查看我的主页啦！👇&#x…...
H5游戏源码分享-密室逃脱小游戏（考验反应能力）
H5游戏源码分享-密室逃脱小游戏（考验反应能力） 预判安全位置，这个需要快速的反应能力 源码 <!DOCTYPE html> <html> <head> <meta http-equiv"Content-Type" content"text/html; charsetutf-8" /&…...
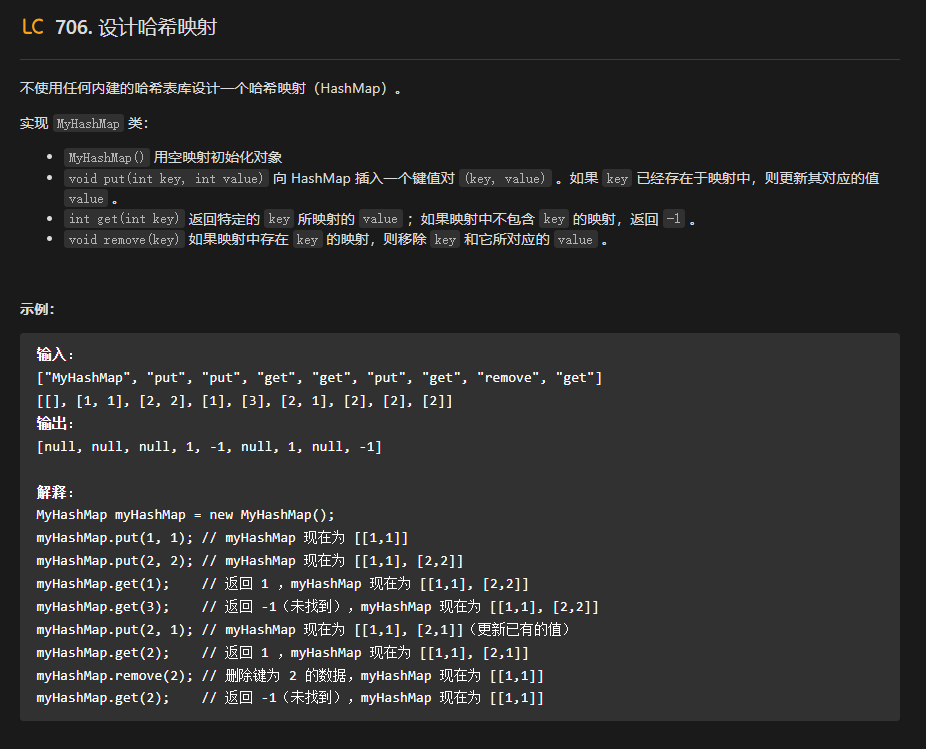
【LeetCode刷题-哈希】--706.设计哈希映射
706.设计哈希映射 class MyHashMap {private class Pair{private int key;private int value;public Pair(int key ,int value){this.key key;this.value value;}public int getKey(){return key;}public int getValue(){return value;}public void setValue(int value){this…...
前端 ： 用HTML ，CSS ,JS 做一个点名器
1.HTML： <body><div id "content"><div id"top"><div id "name">XAiot2302班点名器</div></div><div id "center"><div id "word">你准备好了吗?</di…...
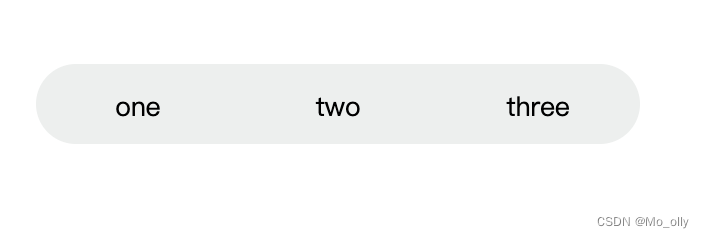
css：button实现el-radio效果
先看最终效果： 思路： 一、 首先准备好按钮内容：const a [one,two,three] 将按钮循环展示出来，并设置一些样式，将按钮背景透明： <button v-for"(item,index) in a" :key"in…...
【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎（Physics Engine） 物理引擎 是一种通过计算机模拟物理规律（如力学、碰撞、重力、流体动力学等）的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互，广泛应用于 游戏开发、动画制作、虚…...
DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑，确保抽奖活动能够公平、公正、公开地进行，同时满足高并发访问、数据安全存储与高效处理等需求，为用户提供流畅的抽奖体验，助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
rknn优化教程（二）
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK，开始写第二篇的内容了。这篇博客主要能写一下： 如何给一些三方库按照xmake方式进行封装，供调用如何按…...
C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj，再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
：观察者模式)
JS设计模式(4)：观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中，我们经常会遇到这样的场景：一个对象的状态变化需要自动通知其他对象，比如： 电商平台中，商品库存变化时需要通知所有订阅该商品的用户；新闻网站中࿰…...
嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集，单周期执行；低功耗、CIP 独立外设；用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel（原始…...
vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
OpenGL-什么是软OpenGL/软渲染/软光栅？
软OpenGL（Software OpenGL）或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式（包括几何处理、光栅化、着色等），不依赖GPU硬件加速。这种模式通常性能较低，但兼容性极强，常用于不支持硬件加速…...
RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...