最短路径:迪杰斯特拉算法
简介
英文名Dijkstra
作用:找到路中指定起点到指定终点的带权最短路径
核心步骤
1)确定起点,终点
2)从未走过的点中选取从起点到权值最小点作为中心点
3)如果满足 起点到中心点权值 + 中心点到指定其他点的权值 < 起点到其他点的权值,
即Weight[start] [center] +Weight [center] [other] < Weight [start] [center] ,
简言之,有更短的路径就取更短的路
理论模拟
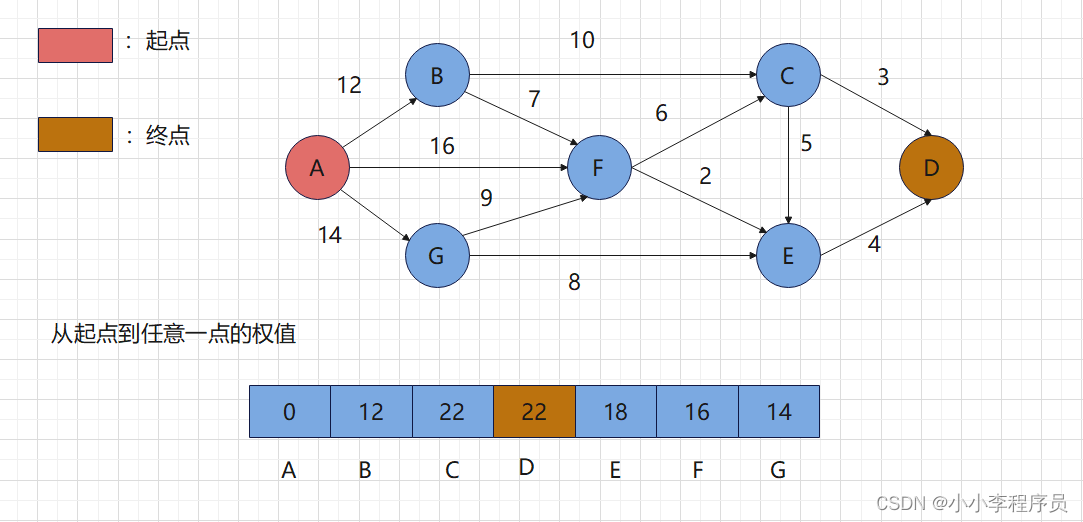
以A为起点,D为终点,如图所示 径, 更新记录更短权值路径

从未走过的点中选取权值最小点,即A作为中心点,标记A走过,更新起点到B、F、G的路径

从未走过的点中选取权值最小点,即B, 并且W:B->C + W:A->C = 12 + 10 < +oo ,更新起点A到C的路径和,
即W: A-> C =W: A-> B -> C =12+10 =22

继续从未走过的点中选取权值最小点G, W: A -> E =+oo > W: A->G ->E =14+8 =22 ,
更新W: A->E 为22

选取F, 由于W:A->F->E=16+2 =18 <22 更新 W: A-> E =18 ,

选取E,由于W:A->E->D=18+4=22<+oo,则更新W: A->D =22

选取C,无可更新点

到达终点D! 最短路径为A->F->E->D ,最短路径和为22
Java代码实现
顶点
//顶点类
public class Vertex {public String Number; //顶点编号public List<Vertex>neighborVertexs; //邻居顶点public Map<Vertex,Integer>weights; //与邻居节点之间的权值public Vertex(String number) {this.Number = number;this.neighborVertexs=new LinkedList<>();this.weights=new HashMap<>();}
}边
public class Edge {public Vertex start;public Vertex end;public Integer weight;public Edge(Vertex start, Vertex end, Integer weight) {this.start = start;this.end = end;this.weight = weight;}
}最短路径返回结果
public class MinPathResult {public String minPathString; //将最短路径拼接成字符串形式,如 A->B->Cpublic List<Vertex>minPathList; //将起点到终点的路径储存在List集合中public Integer minPathSum; //记录起点到终点的最短路径和public MinPathResult(List<Vertex> minPathList, String minPathString,Integer minPathSum) {this.minPathString = minPathString;this.minPathList = minPathList;this.minPathSum=minPathSum;}@Overridepublic String toString() {return "Result{" +"minPathString:'" + minPathString +" minPathSum:"+minPathSum+'}';}
}Dijkstra算法的实现,适用于无向图
import java.util.*;
//适用于无向图
public class DijkstraOperator {private List<Vertex>vertexs; //全部顶点private List<Edge>edges; //所有边private Map<String,Vertex>vertexs_map; //通过顶点编号找到顶点private final static Integer INF=Integer.MAX_VALUE; //代表无穷大public DijkstraOperator(List<Vertex> vertexs, List<Edge> edges) {this.vertexs = vertexs;this.edges = edges;this.vertexs_map=new HashMap<>();//构建编号映射顶点for(Vertex v:vertexs){vertexs_map.put(v.Number,v);}//填充所有顶点的邻居以及权值for(int i=0;i<edges.size();i++){//填充起点的邻居,以及起点到终点的权值edges.get(i).start.neighborVertexs.add(edges.get(i).end);edges.get(i).start.weights.put(edges.get(i).end,edges.get(i).weight);//填充终点的邻居,以及终点到起点的权值edges.get(i).end.neighborVertexs.add(edges.get(i).start);edges.get(i).end.weights.put(edges.get(i).start,edges.get(i).weight);}}//获得从起点到终点之间的路径public MinPathResult getMinPath(String start, String end){//用哈希表标记某个顶点是否走过Map<Vertex,Boolean>visited=new HashMap<>();//用哈希表记录顶点的前驱Map<Vertex,Vertex>preVertex=new HashMap<>();//利用哈希表记录起点到任意一点的最短路径Map<Vertex,Integer>minPath=new HashMap<>();//初始化三个表for(int i=0;i<vertexs.size();i++){//初始化每一个点都未走过visited.put(vertexs.get(i),false);//初始化每个点的前驱都是自己preVertex.put(vertexs.get(i),vertexs.get(i));//初始化起点到任意两个点之间的最短路径都是无穷大minPath.put(vertexs.get(i),INF);}Vertex startVertex=vertexs_map.get(start);Vertex endVertex=vertexs_map.get(end);//填充存在的路径for(int i=0;i<startVertex.neighborVertexs.size();i++){//设置起点与邻居节点之间的权值minPath.put(startVertex.neighborVertexs.get(i),startVertex.weights.get(startVertex.neighborVertexs.get(i)));//设置点前驱preVertex.put(startVertex.neighborVertexs.get(i),startVertex);}//自己到自己的距离为0minPath.put(startVertex,0);Vertex curVertex=null;//一直寻路,直到找到终点while(curVertex!=endVertex){Integer minWeight=Integer.MAX_VALUE;curVertex=null;//能看到的点之间选取距离最小的那个,且这个点并没有走过for(Vertex v:minPath.keySet()){if(!visited.get(v)&&minPath.get(v)<minWeight){//切换中心点curVertex=v;//更新最小权值minWeight=minPath.get(v);}}//如果找不到下一个中心点,说明从起点根本到达不来终点if(curVertex==null)return null;//标记选取点visited.put(curVertex,true);//更新权值for(int i=0;i<curVertex.neighborVertexs.size();i++){//邻居节点Vertex neighborVertex=curVertex.neighborVertexs.get(i);//计算起点到邻居节点之间新的权值int newWeight=minPath.get(curVertex)+curVertex.weights.get(neighborVertex);//找到能移动的点,如果转折之后距离更短,则记录更短的距离if(visited.get(neighborVertex)==false&&newWeight<minPath.get(neighborVertex)){//记录更短距离minPath.put(neighborVertex,newWeight);//记录邻居节点的前驱preVertex.put(neighborVertex,curVertex);}}}//起点到终点之间的最短路径LinkedList<Vertex>targetPath=new LinkedList<>();for(Vertex curVer=endVertex;curVer!=startVertex;curVer=preVertex.get(curVer)){targetPath.addFirst(curVer);}targetPath.addFirst(startVertex);//拼接最短路径StringBuffer minPathStringBuffer=new StringBuffer();Integer pathSum=0;for(int i=0;i< targetPath.size();i++){minPathStringBuffer.append(targetPath.get(i).Number);if(i!= targetPath.size()-1){pathSum=pathSum+targetPath.get(i).weights.get(targetPath.get(i+1));minPathStringBuffer.append("->");}}return new MinPathResult(targetPath, minPathStringBuffer.toString(),pathSum);}
}测试函数
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);List<Vertex>vertexs=new LinkedList<>();List<Edge>edges=new LinkedList<>();System.out.println("请输入顶点的数量:");Integer vexcnt= scanner.nextInt();System.out.println("请输入这些顶点编号:");for(int i=0;i<vexcnt;i++){vertexs.add(new Vertex(scanner.next()));}System.out.println("请输入边的数量:");Integer edgecnt= scanner.nextInt();System.out.println("请输入这些边的端点编号和权值:");for(int i=0;i<edgecnt;i++){String number1= scanner.next();String number2= scanner.next();Integer weight= scanner.nextInt();Vertex v1=null;Vertex v2=null;for(int j=0;j<vertexs.size();j++){if(vertexs.get(j).Number.equals(number1))v1=vertexs.get(j);if(vertexs.get(j).Number.equals(number2))v2=vertexs.get(j);}edges.add(new Edge(v1,v2,weight));}//定义迪杰斯特拉操作类DijkstraOperator dijkstra=new DijkstraOperator(vertexs,edges);//获取任意两点之间的最短路径结果集List<MinPathResult>minPathResults=new ArrayList<>();for(int i=0;i< vertexs.size();i++){for(int j=i+1;j< vertexs.size();j++){minPathResults.add(dijkstra.getMinPath(vertexs.get(i).Number,vertexs.get(j).Number));System.out.println(minPathResults.get(minPathResults.size()-1));}}}
}测试输入与输出结果
//输入部分
请输入顶点的数量:
7
请输入这些顶点编号:
A B C D E F G
请输入边的数量:
12
请输入这些边的端点编号和权值:
A B 12
A F 16
A G 14
B C 10
B F 7
G F 9
G E 8
F C 6
F E 2
C D 3
C E 5
E D 4//输出部分
Result{minPathString:'A->B minPathSum:12}
Result{minPathString:'A->B->C minPathSum:22}
Result{minPathString:'A->F->E->D minPathSum:22}
Result{minPathString:'A->F->E minPathSum:18}
Result{minPathString:'A->F minPathSum:16}
Result{minPathString:'A->G minPathSum:14}
Result{minPathString:'B->C minPathSum:10}
Result{minPathString:'B->F->E->D minPathSum:13}
Result{minPathString:'B->F->E minPathSum:9}
Result{minPathString:'B->F minPathSum:7}
Result{minPathString:'B->F->G minPathSum:16}
Result{minPathString:'C->D minPathSum:3}
Result{minPathString:'C->E minPathSum:5}
Result{minPathString:'C->F minPathSum:6}
Result{minPathString:'C->E->G minPathSum:13}
Result{minPathString:'D->E minPathSum:4}
Result{minPathString:'D->E->F minPathSum:6}
Result{minPathString:'D->E->G minPathSum:12}
Result{minPathString:'E->F minPathSum:2}
Result{minPathString:'E->G minPathSum:8}
Result{minPathString:'F->G minPathSum:9}进程已结束,退出代码为 0相关文章:

最短路径:迪杰斯特拉算法
简介 英文名Dijkstra 作用:找到路中指定起点到指定终点的带权最短路径 核心步骤 1)确定起点,终点 2)从未走过的点中选取从起点到权值最小点作为中心点 3)如果满足 起点到中心点权值 中心点到指定其他点的权值 < 起…...
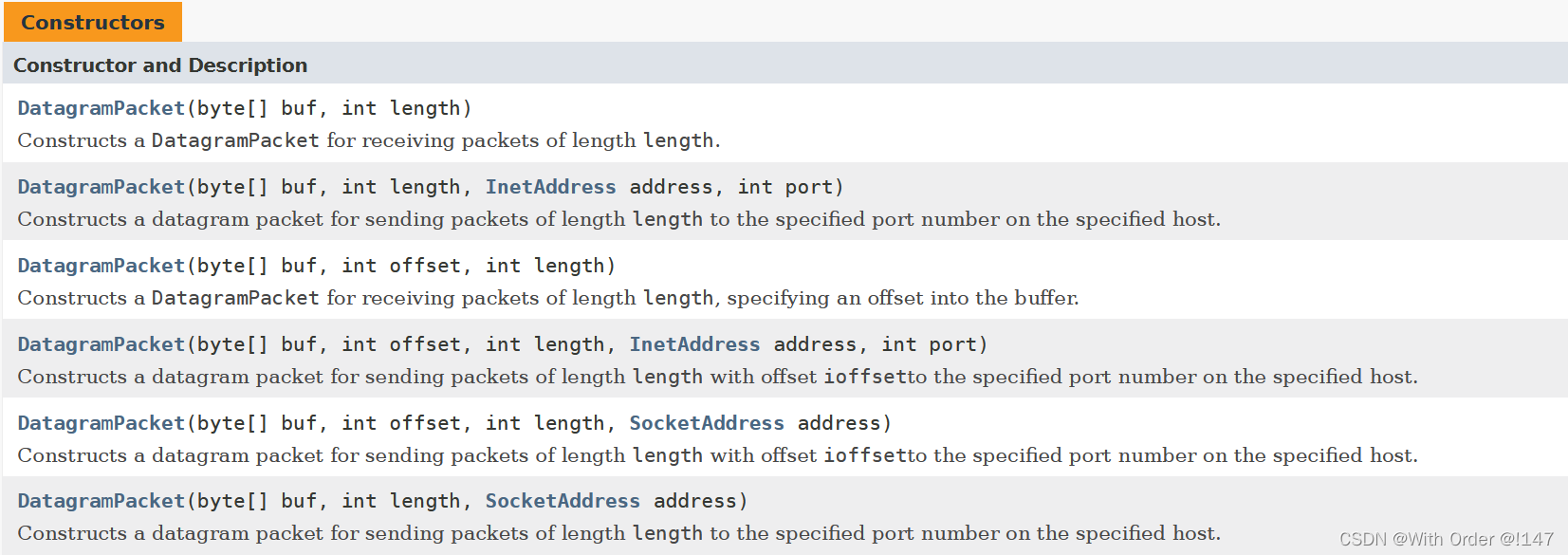
基于UDP/TCP的网络通信编程实现
小王学习录 今日鸡汤Socket套接字基于UDP来实现一个网络通信程序DatagramSocket类DatagramPacket类基于UDP的服务器端代码基于UDP的客户端代码基于TCP来实现一个网络通信程序ServerSocket类Socket类基于TCP的服务器端代码基于TCP的客户端代码优化之后的服务器端代码补充TCP长短…...
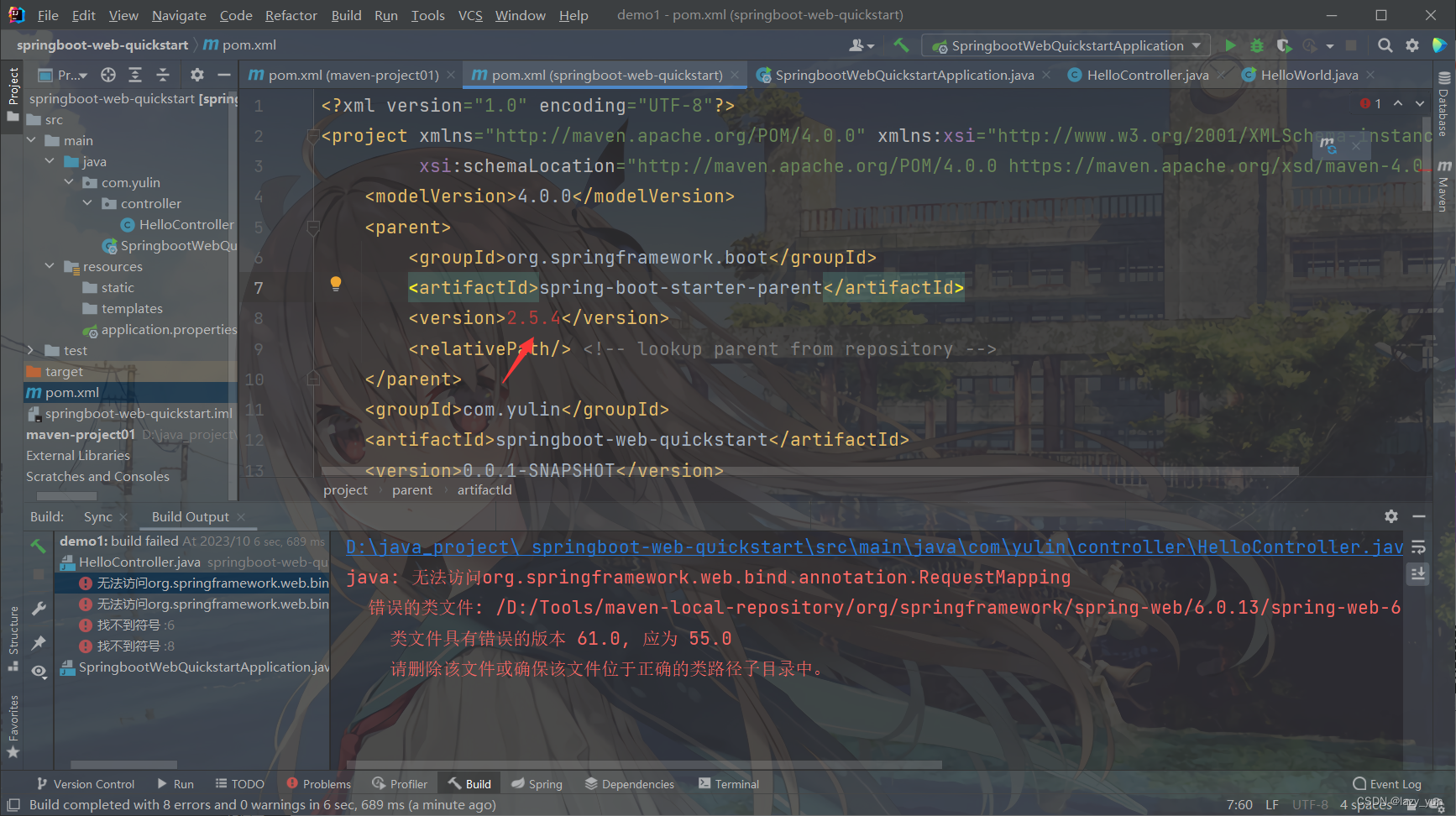
springboot启动报错
...
函数)
Python中的split()函数
函数:split() Python中有split()和os.path.split()两个函数,具体作用如下: split():拆分字符串。通过指定分隔符对字符串进行切片,并返回分割后的字符串列表(list) os.path.split():…...

大数据-玩转数据-Python Sftp Mysql 数据
一、需求描述 1、从Mysql数据库表下载数据到服务器; 2、将数据已csv文件格式存储并对数据格式进行处理(添加表头,表头和数据均用竖线分隔符隔开,末尾也加分割符); 3、文件路径文件夹以天为单位,…...
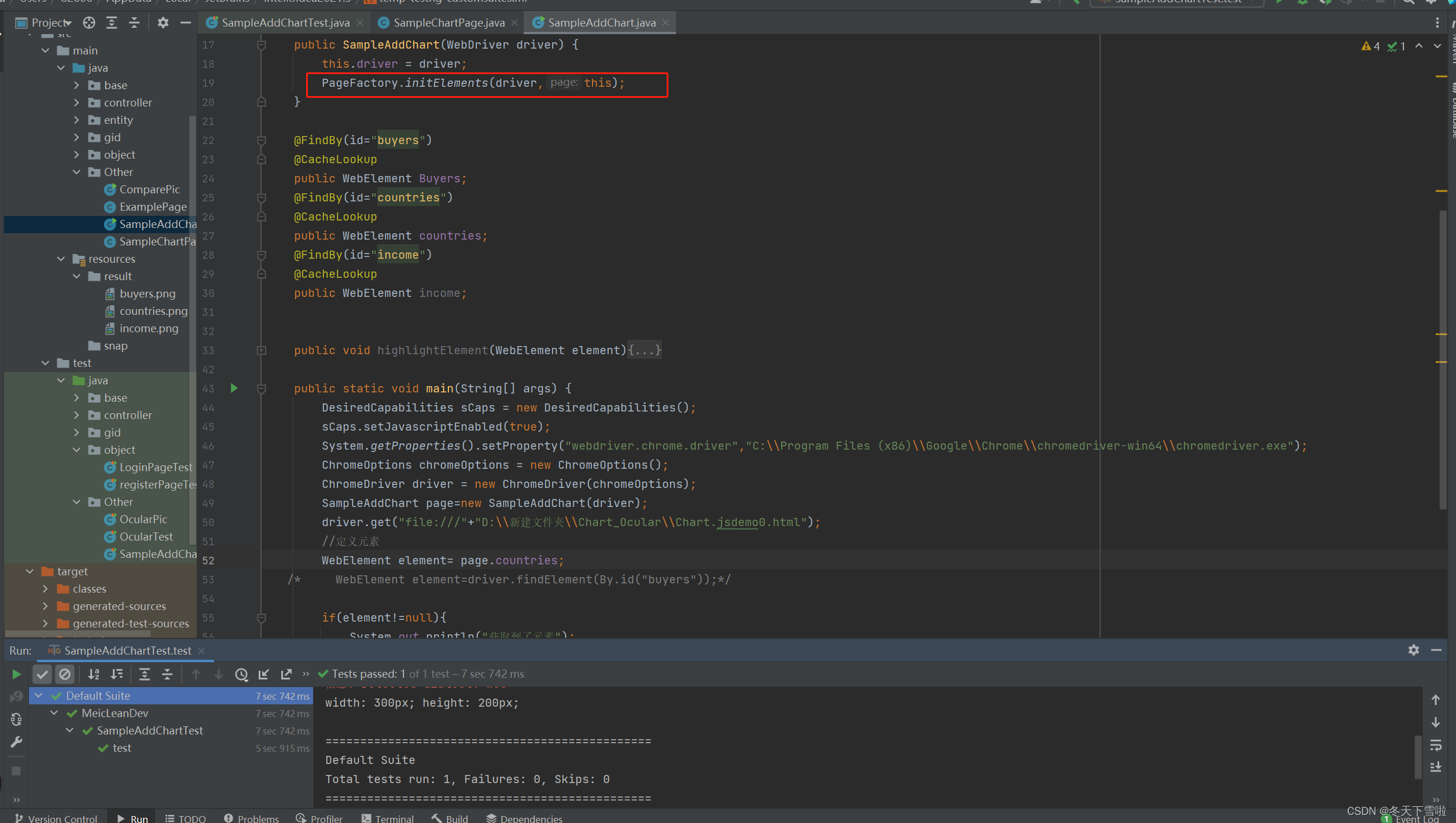
Selenium3-当元素通过@FindBy获取时,返回元素为null
报错: 在获取元素的js属性时一直获取不到,报空指针,定位到元素时,发现是FindBy的元素没有找到 解决方法: 在page类的构造函数中加上了 界面初始化,让元素先隐式加载,这样就不会出现返回元素为空的情况辣 PageFactory…...

JWT详解解读读
📑前言 本文主要是jwt解读文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 🌄每日一句:努力一点&#…...
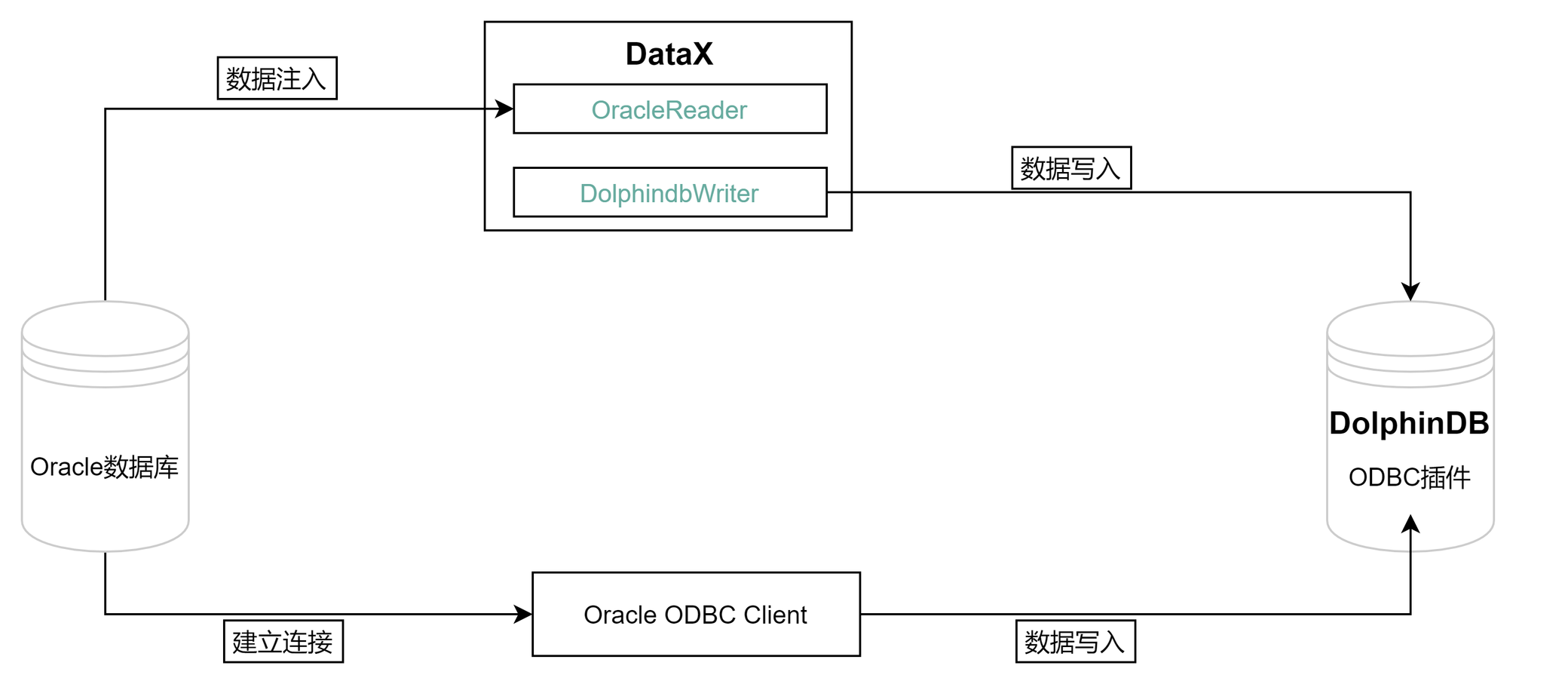
一文详解如何从 Oracle 迁移数据到 DolphinDB
Oracle 是一个广泛使用的关系型数据库管理系统,它支持 ACID 事务处理,具有强大的安全性和可靠性,因此被广泛应用于各种企业级应用程序。但是,随着数据规模的增加和业务需求的变化,Oracle 的一些限制和缺点也逐渐暴露出…...
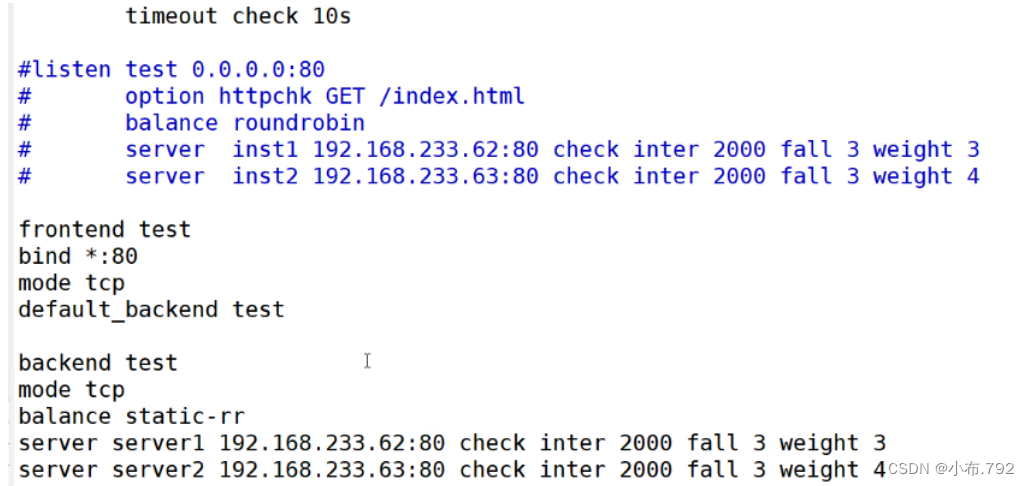
负载均衡--Haproxy
haproxy 他也是常用的负载均衡软件 nginx 支持四层转发,七层转发 haproxy也可以四层和七层转发 haproxy:法国人开发的威利塔罗在2000年基于C语言开发的一个开源软件 可以支持一万以上的并发请求 高性能的tcp和http负载均衡2.4 1.5.9 haproxy&#…...

股票价格预测 | 融合CNN和Transformer以提升股票趋势预测准确度
一 本文摘要 股票价格往往很难预测,因为我们很难准确建模数据点之间的短期和长期时间关系。卷积神经网络(CNN)擅长找出用于建模短期关系的局部模式。然而,由于其有限的观察范围,CNN无法捕捉到长期关系。相比之下,Transformer可以学习全局上下文和长期关系。本文提出了一…...

QMI8658A_QMC5883L(9轴)-EVB 评估板
1. 描述 QMI8658A_QMC5883L(9轴)-EVB 评估板是一款功能强大的9轴IMU传感器,它利用了QMA8658A 内置的3轴加速度计和3轴陀螺仪,同时结合QMC5883L的3轴地磁数据,来测量物体在三维空间中的角速度和加速度(严格意义上的IMU只为用户提供…...
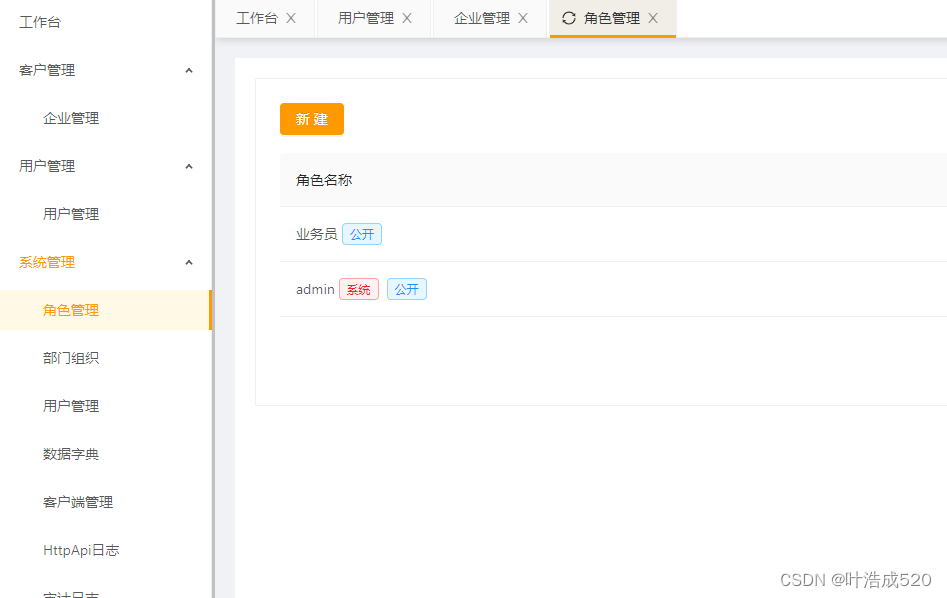
vue2+antd——实现动态菜单路由功能——基础积累
vue2antd——实现动态菜单路由功能——基础积累 实现的需求:效果图:登录接口处添加以下代码loadRoutes方法内容如下: 最近在写后台管理系统,遇到一个需求就是要将之前的静态路由改为动态路由,使用的后台框架是…...
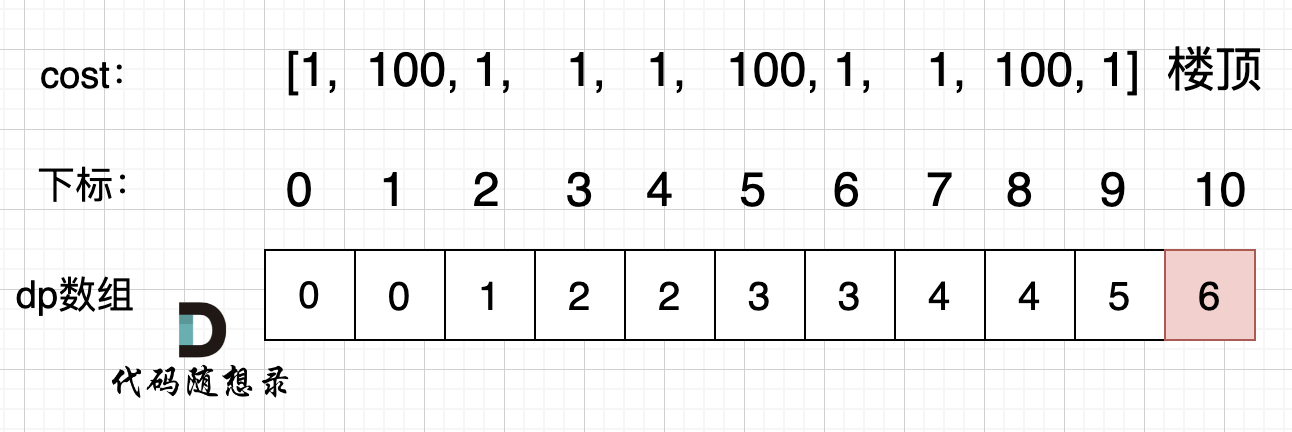
代码随想录算法训练营第三十八天丨 动态规划part01
动态规划理论基础 动态规划刷题大纲 什么是动态规划 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 所以动态规划中每一个状态一定是由上一个状态推导出来的&a…...
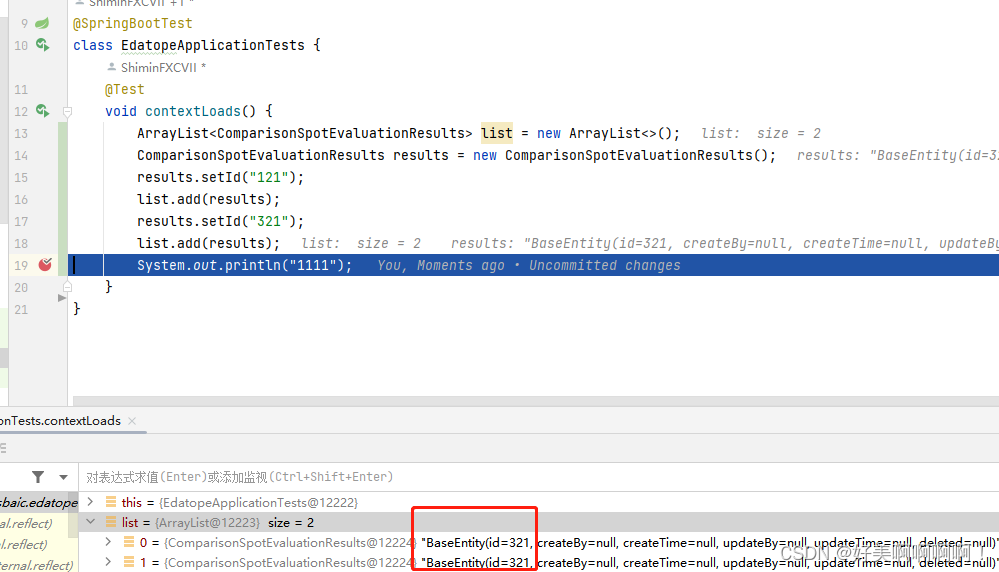
关于集合遇到的坑
public void invoke(ComparisonSpotEvaluationResultsExcel comparisonSpotEvaluationResultsExcel, AnalysisContext analysisContext) {/*** 记录行号码*/ReadRowHolder readRowHolder analysisContext.readRowHolder();Integer rowIndex readRowHolder.getRowIndex();Stri…...

需要下微信视频号视频的小伙伴们看过来~
随着视频号的热度越来越大,下载视频号视频的需求也开始增加啦,今天给大家给分享几个简单实用的下载方法,总有一个你能用上的! 一、犀牛视频下载 犀牛视频下载器可以直接解析并下载视频号短视频。您只需转发视频到机器人即可下载。…...

测试工具:hurl
文章目录 Hurlinstallstartdemo 功能使用变量Capturing values 捕获值Asserts 断言生成报告 Hurl 官网:https://hurl.dev/ Hurl 是一个命令行工具,它运行以简单的纯文本格式定义的 HTTP 请求。 它可以发送请求、捕获值并评估对标头和正文响应的查询 i…...

RateLimiter限流
使用场景 限流是高并发的处理方法之一。 高并发处理方案: 缓存:缓存的目的是提升系统访问速度和增大系统处理容量。 降级:降级是当服务出现问题或者影响到核心流程时,需要暂时屏蔽掉,待高峰或者问题解决后再打开。…...
PMP适合哪些人去考?
许多人都在考虑是否适合考取PMP证书,我来解答你的疑惑:无论是IT、建筑、制药、制造业、电信、金融还是通信领域,PMP证书都得到广泛认可。虽然IT行业目前占比最大,但近几年T业比重下降,制造业、金融、能源和建筑工程等的…...

钡铼技术 工控机中的X86和ARM处理器:哪个更具可扩展性?
X86和ARM是两种不同的处理器架构,它们在工控机中的应用也有所不同。 X86架构的处理器是英特尔公司和AMD公司生产的,它们主要应用于个人电脑和服务器等领域。X86架构的处理器具有良好的通用性和兼容性,可以运行各种操作系统和应用软件。X86架…...
)
软考 系统架构设计师系列知识点之软件构件(3)
接前一篇文章:软考 系统架构设计师系列知识点之软件构件(2) 所属章节: 第2章. 计算机系统基础知识 第3节. 计算机软件 2.3.7 软件构件 (2)J2EE(补充知识) J2EE核心组成:…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
