当前位置： 首页 > news >正文

python实现ModBusRTU服务端

news 2026/2/10 7:34:18

python实现基于串口通信的ModBusRTU服务端是一件简单的事情，只要通过pymodbus模块和Serial模块就可以实现。

相关文章：

python实现ModBusRTU服务端

python实现基于串口通信的ModBusRTU服务端是一件简单的事情，只要通过pymodbus模块和Serial模块就可以实现。...

编程日记 2023/10/30 15:43:44

yum安装node,npm

node官网 yum -y install nodejs npm 查看版本 npm -v node -v卸载 yum -y remove nodejs npm修改镜像源 4.1. 修改淘宝镜像源 set registry https://registry.npm.taobao.org npm config get registr4.2. 修改华为云镜像源 npm config set registry https://mirrors.huaweicl…...

编程日记 2023/10/30 15:41:42

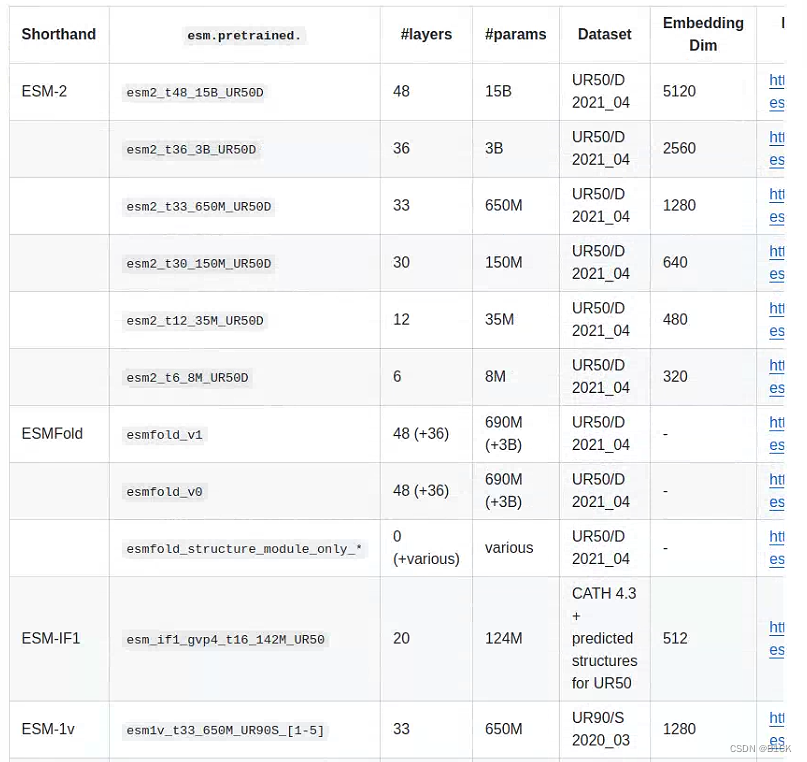
ESM蛋白质语言模型系列

模型总览 第一篇《Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences 》ESM-1b 第二篇《MSA Transformer》在ESM-1b的基础上作出改进，将模型的输入从单一蛋白质序列改为MSA矩阵，并在Tran…...

编程日记 2023/10/30 15:40:42

RHCE-------Day1

存储管理 标准存储管理 1、分区 fdisk /dev/nume0n1 交互式指令 2、格式化 mkfs.xfs /dev/nume0n1p1 直接指定分区类型 mkfs -t xfs /dev/nume0n1p1 3、挂载 mount /dev/nume0n1p1 /mnt 取消挂载： umont …...

编程日记 2023/10/30 15:39:40

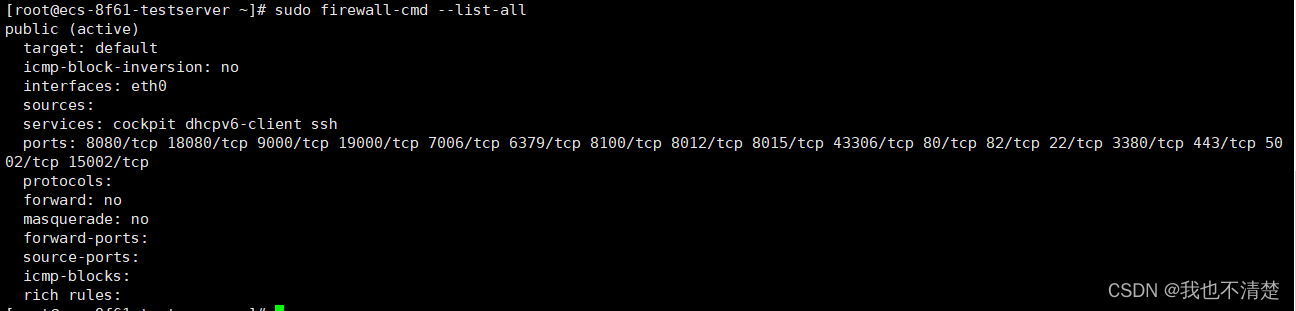
Linux(Centos7)防火墙端口操作记录

1、nginx -t #Nginx配置文件检查 上述截图代表检查没问题 上述截图检查配置文件配置错误，并提示错误文件位置 2、systemctl restart nginx #重启Nginx 重启Nginx失败 3、systemctl status nginx.service #查看Nginx服务状态 80端口被占导致服务启动失败 4、n…...

编程日记 2023/10/30 15:38:39

【MySQL数据库】初识MySQL数据库、安装MySQL

文章目录 前言一、什么是 MySQL？二、MySQL 的强大之处三、Ubuntu安装MySQL步骤 1: 更新包列表步骤 2: 安装 MySQL步骤 3: 启动 MySQL 服务步骤 4: 验证 MySQL 安装步骤 5: 确保 MySQL 安全性 总结 前言 在今天的数字化世界中，数据是企业和个人的重要资产…...

编程日记 2023/10/30 15:36:37

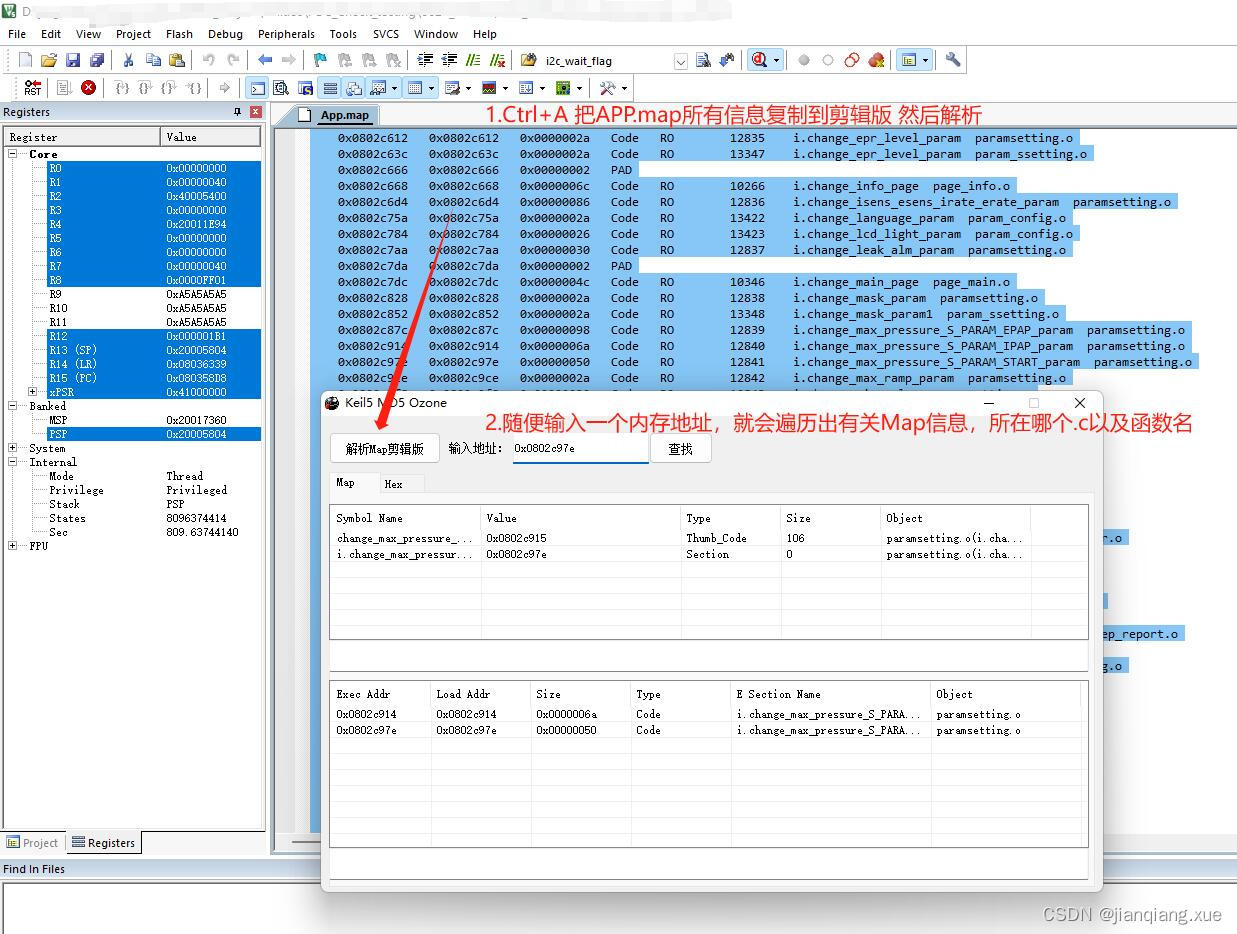
Keil Map信息解析

基本功能： 1.在Keil里面，通过App.Map复制所有信息。然后解析剪辑版内容。 2.随意输入一个函数内存地址，即可遍历出该内存地址属于哪个.c或者函数名。或者能遍历出变量。 强化功能： 1.通过Keil5 命令 Save xxxxxxx\1.Hex 0x200173…...

编程日记 2023/10/30 15:35:36

在重生奇迹MU中如何选择最佳的挂机点？

如何寻找最适合自己的挂机地点呢？小编建议玩家朋友从以下几点着手加以抉择。 怪物的等级不能过高 你的最佳挂机点要结合自己的实际情况来定，如果你刷怪比较吃力的话，那么此游戏地图并不适合你挂机，一旦挂机过程中，你…...

编程日记 2023/10/30 15:34:35

IT行业中的热门职业及前景展望

目录 一、IT技术发展背景及历程 二、IT行业热门职业 三、前景展望 一、IT技术发展背景及历程 随着科技的不断发展和创新，IT技术也在不断更新和完善。从计算机的出现到互联网的普及，再到现代云计算、人工智能等技术的兴起，IT技术已经成为了…...

编程日记 2023/10/30 15:33:34

linux练习

linux练习 vim编辑器有哪几种工作模式？ 命令模式、末行模式、编辑模式 yum的配置文件在什么目录下？具体有哪些字段？ 目录：cat /etc/yum.repos.d/*.repo 字段： [] name baseurl enabled gpgcheck 规划分区的命令是什么…...

编程日记 2023/10/30 15:32:33

【【带有握手信号的无符号数乘法verilog+ testbench 代码】】

带有握手信号的无符号数乘法verilog testbench 代码 uumultiplier.v module uumultiplier #(parameter NUMBER1 8 ,parameter NUMBER2 …...

编程日记 2023/10/30 15:31:32

【Python机器学习】零基础掌握BayesianRidge贝叶斯回归

如何准确预测房价？ 在现实生活中，购买房产可能是最大的一笔投资。因此，准确预测房价变得尤为重要。通常，房价受到多个因素的影响，包括地段、房龄、房屋面积等。但如何综合这些因素来做出准确预测呢？ 这里介绍一种机器学习算法：贝叶斯岭回归（Bayesian Ridge Regressio…...

编程日记 2023/10/30 15:30:31

【机器学习】朴素贝叶斯算法基本原理与计算案例

朴素贝叶斯算法基本原理与计算案例 文章目录 朴素贝叶斯算法基本原理与计算案例1. 朴素贝叶斯算法的基本原理2. 概率基础3. 朴素贝叶斯简单计算案例4. 朴素贝叶斯算法对文本进行分类5. 拉普拉斯平滑系数6. 案例：20类新闻分类7. 总结 1. 朴素贝叶斯算法的基本原理 朴…...

编程日记 2023/10/30 15:29:30

redis6.0源码分析：简单动态字符串sds

文章目录 sds简介与特性(面试)sds结构模型数据结构苛刻的数据优化数据结构优化uintX_t对齐填充 sds优势O(1)时间复杂度获取字符串长度二进制安全杜绝缓冲区溢出自动扩容机制——sdsMakeRoomFor方法 内存重分配次数优化 sds最长是多少部分API源码解读创建sds释放sds sds简介与特…...

编程日记 2023/10/30 15:28:29

1.7 攻击面和攻击树

思维导图： 1.7 攻击面与攻击树 攻击面: 描述计算机和网络系统面对的安全威胁和攻击。 定义: 攻击面是由系统中可访问和可利用的漏洞所组成。常见攻击面: 向外部Web及其他服务器开放的端口和相应代码。防火墙内部的服务。处理入站数据、电子邮件、XML文件、Office文档…...

编程日记 2023/10/30 15:27:28

解决input在谷歌浏览器自动填充问题

解决input在谷歌浏览器自动填充问题 <input typepassword readonly onfocus"this.removeAttribute(readonly);" />...

编程日记 2023/10/30 15:26:27

Java字节码技术

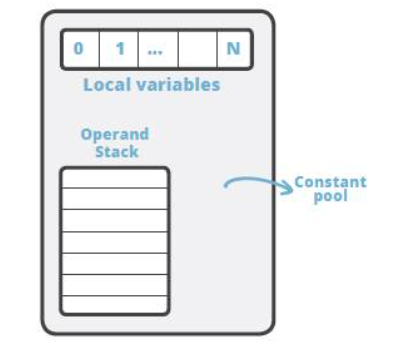
Java 字节码简介 Java 中的字节码&#xff0c;英文名为 bytecode, 是 Java 代码编译后的中间代码格式。JVM 需要读取并解析字节码才能执行相应的任务。 从技术人员的角度看&#xff0c;Java 字节码是 JVM 的指令集。JVM 加载字节码格式的 class 文件&#xff0c;校验之后通过 J…...

编程日记 2023/10/30 15:23:22

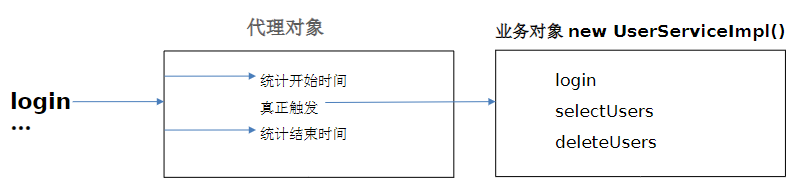
Java SE 学习笔记（十八）—— 注解、动态代理

目录 1 注解1.1 注解概述1.2 自定义注解1.3 元注解1.4 注解解析1.5 注解应用于 junit 框架 2 动态代理2.1 问题引入2.2 动态代理实现 1 注解 1.1 注解概述 Java 注解&#xff08;Annotation&#xff09;又称Java标注&#xff0c;是JDK 5.0引入的一种注释机制&#xff0c;Java语…...

编程日记 2023/10/30 15:22:21

虚拟内存之请求分页管理

一、与基本分页存储管理的区别 程序执行过程中&#xff0c;访问信息不在内存时&#xff0c;OS需要从外存调入内存。——>调页功能 内存空间不够时&#xff0c;OS需要将内存中暂时用不到的信息换出到外存。——>页面置换功能 二、页表机制 1.页表&#xff1a;需要知道页面…...

编程日记 2023/10/30 15:21:19

lazarus开发：提升sqlite数据插入速度

目录 1 前言 2 优化数据容器 3 开启事务插入数据 4 其他方面优化 1 前言 近期有一个需求是向数据库中插入excel文件中的10万多条数据&#xff0c;接近70个字段。最初整个插入数据时间是大约40分钟&#xff0c;经过优化调整后&#xff0c;大幅优化为大约5分钟。这里简单介绍…...

编程日记 2023/10/30 15:20:17

铭豹扩展坞 USB转网口 突然无法识别解决方法

当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...

编程新知 2026/2/9 16:05:07

业务系统对接大模型的基础方案：架构设计与关键步骤

业务系统对接大模型&#xff1a;架构设计与关键步骤 在当今数字化转型的浪潮中&#xff0c;大语言模型&#xff08;LLM&#xff09;已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中&#xff0c;不仅可以优化用户体验&#xff0c;还能为业务决策提供…...

编程新知 2026/2/8 4:53:03

【kafka】Golang实现分布式Masscan任务调度系统

要求&#xff1a; 输出两个程序&#xff0c;一个命令行程序&#xff08;命令行参数用flag&#xff09;和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽&#xff0c;然后将消息推送到kafka里面。 服务端程序&#xff1a; 从kafka消费者接收…...

编程新知 2026/2/8 20:41:58

shell脚本--常见案例

1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件&#xff1a; 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

编程新知 2026/2/7 19:53:11

系统设计 --- MongoDB亿级数据查询优化策略

系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log&#xff0c;共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题&#xff0c;不能使用ELK只能使用…...

编程新知 2026/1/4 3:47:09

STM32F4基本定时器使用和原理详解

STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

编程新知 2026/2/9 3:58:32

EtherNet/IP转DeviceNet协议网关详解

一&#xff0c;设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络&#xff0c;本网关连接到EtherNet/IP总线中做为从站使用&#xff0c;连接到DeviceNet总线中做为从站使用。 在自动…...

编程新知 2026/1/31 6:53:51

Unit 1 深度强化学习简介

Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库&#xff0c;例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体&#xff0c;比如 SnowballFight、Huggy the Do…...

编程新知 2026/2/8 12:54:53

实现弹窗随键盘上移居中

实现弹窗随键盘上移的核心思路 在Android中&#xff0c;可以通过监听键盘的显示和隐藏事件&#xff0c;动态调整弹窗的位置。关键点在于获取键盘高度&#xff0c;并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

编程新知 2025/10/6 18:46:56

如何理解 IP 数据报中的 TTL？

目录 前言理解 前言 面试灵魂一问&#xff1a;说说对 IP 数据报中 TTL 的理解&#xff1f;我们都知道&#xff0c;IP 数据报由首部和数据两部分组成&#xff0c;首部又分为两部分&#xff1a;固定部分和可变部分&#xff0c;共占 20 字节&#xff0c;而即将讨论的 TTL 就位于首…...

编程新知 2026/2/4 18:09:49