分类预测 | Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制)
分类预测 | Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制)
目录
- 分类预测 | Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制)
- 分类效果
- 基本描述
- 程序设计
- 参考资料
分类效果






基本描述
1.Matlab实现KOA-CNN-LSTM-selfAttention开普勒算法优化卷积长短期记忆神经网络融合自注意力多特征分类预测,多特征输入模型,运行环境Matlab2023b及以上;
2.基于开普勒算法(KOA)优化卷积长短期记忆神经网络(CNN-LSTM)结合自注意力机制(selfAttention)分类预测。2023年新算法KOA,MATLAB程序,多行变量特征输入,优化了学习率、卷积核大小及隐藏层单元数等。
3.多特征输入单输出的二分类及多分类模型。程序内注释详细,直接替换数据就可以用。程序语言为matlab,程序可出分类效果图,迭代图,混淆矩阵图.
4.data为数据集,输入12个特征,分四类;main为主程序,其余为函数文件,无需运行。
5.输出指标包括优化参数、精确度、召回率、精确率、F1分数。
程序设计
- 完整程序和数据获取方式,私信博主回复Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制)。
[Order] = sort(PL_Fit); %% 对当前种群中的解的适应度值进行排序%% 函数评估t时的最差适应度值worstFitness = Order(SearchAgents_no); %% Eq.(11)M = M0 * (exp(-lambda * (t / Tmax))); %% Eq.(12)%% 计算表示太阳与第i个解之间的欧几里得距离Rfor i = 1:SearchAgents_noR(i) = 0;for j = 1:dimR(i) = R(i) + (Sun_Pos(j) - Positions(i, j))^2; %% Eq.(7)endR(i) = sqrt(R(i));end%% 太阳和对象i在时间t的质量计算如下:for i = 1:SearchAgents_nosum = 0;for k = 1:SearchAgents_nosum = sum + (PL_Fit(k) - worstFitness);endMS(i) = rand * (Sun_Score - worstFitness) / (sum); %% Eq.(8)m(i) = (PL_Fit(i) - worstFitness) / (sum); %% Eq.(9)end%% 第2步:定义引力(F)% 计算太阳和第i个行星的引力,根据普遍的引力定律:for i = 1:SearchAgents_noRnorm(i) = (R(i) - min(R)) / (max(R) - min(R)); %% 归一化的R(Eq.(24))MSnorm(i) = (MS(i) - min(MS)) / (max(MS) - min(MS)); %% 归一化的MSMnorm(i) = (m(i) - min(m)) / (max(m) - min(m)); %% 归一化的mFg(i) = orbital(i) * M * ((MSnorm(i) * Mnorm(i)) / (Rnorm(i) * Rnorm(i) + eps)) + (rand); %% Eq.(6)end
% a1表示第i个解在时间t的椭圆轨道的半长轴,
for i = 1:SearchAgents_noa1(i) = rand * (T(i)^2 * (M * (MS(i) + m(i)) / (4 * pi * pi)))^(1/3); %% Eq.(23)
endfor i = 1:SearchAgents_no
% a2是逐渐从-1到-2的循环控制参数
a2 = -1 - 1 * (rem(t, Tmax / Tc) / (Tmax / Tc)); %% Eq.(29)% ξ是从1到-2的线性减少因子
n = (a2 - 1) * rand + 1; %% Eq.(28)
a = randi(SearchAgents_no); %% 随机选择的解的索引
b = randi(SearchAgents_no); %% 随机选择的解的索引
rd = rand(1, dim); %% 按照正态分布生成的向量
r = rand; %% r1是[0,1]范围内的随机数%% 随机分配的二进制向量
U1 = rd < r; %% Eq.(21)
O_P = Positions(i, :); %% 存储第i个解的当前位置%% 第6步:更新与太阳的距离(第3、4、5在后面)
if rand < rand% h是一个自适应因子,用于控制时间t时太阳与当前行星之间的距离h = (1 / (exp(n * randn))); %% Eq.(27)% 基于三个解的平均向量:当前解、迄今为止的最优解和随机选择的解Xm = (Positions(b, :) + Sun_Pos + Positions(i, :)) / 3.0;Positions(i, :) = Positions(i, :) .* U1 + (Xm + h .* (Xm - Positions(a, :))) .* (1 - U1); %% Eq.(26)
else参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229
相关文章:

分类预测 | Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制)
分类预测 | Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制) 目录 分类预测 | Matlab实现KOA-CNN-LSTM-selfAttention多特征分类预测(自注意力机制)分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Mat…...
博客系统-项目测试
自动化博客项目 用户注册登录验证效验个人博客列表页博客数量不为 0 博客系统主页写博客 我的博客列表页效验 刚发布的博客的标题和时间查看 文章详情页删除文章效验第一篇博客 不是 "自动化测试" 注销退出到登录页面,用户名密码为空 用户注册 Order(1)Parameterized…...

Inspeckage,动态分析安卓 APP 的 Xposed 模块
前提 我在不久前写过《 APP 接口拦截与参数破解》的博文;最近爬取APP数据时又用到了相关技术,故在此详细描述一下 Inspeckage 的功能。(环境准备本文不再赘述) 功能 在电脑上访问 http://127.0.0.1:8008 就可以看到 inspeckage…...
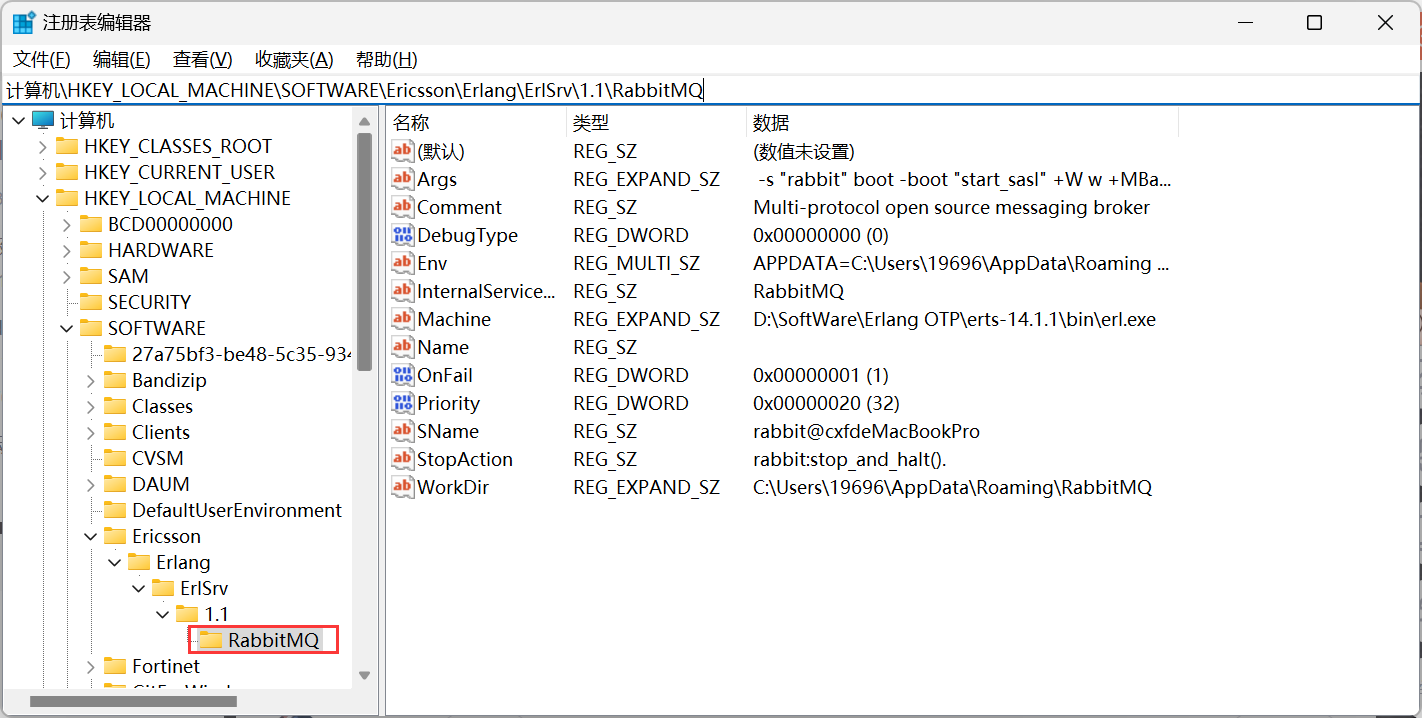
Windows详细安装和彻底删除RabbitMQ图文流程
RabbiitMQ简介 RabbitMQ是实现了高级消息队列协议(AMQP:Advanced Message Queue Protocol)的开源消息代理软件(亦称面向消息的中间件)。RabbitMQ服务器是用Erlang语言编写的,而聚类和故障转移是构建在开放…...

自定义表单规则
const checkF (rule, value, callback) > { if (!value || value ) { callback(new Error(请输入XXXX)); } else { var params new URLSearchParams(); params.append(参数名, value); axios.post(url, params).then(operation > { if (operation && operatio…...

Spring 中 Bean 的作用域有哪些?Spring 中有哪些方式可以把 Bean 注入到 IOC 容器?
Spring 框架里面的 IOC 容器,可以非常方便的去帮助我们管理应用里面的Bean 对象实例。我们只需要按照 Spring 里面提供的 xml 或者注解等方式去告诉 IOC 容器,哪些 Bean需要被 IOC 容器管理就行了。 生命周期 既然是 Bean 对象实例的管理,那意…...

【01低功耗蓝牙开发】
低功耗蓝牙 低功耗蓝牙背后有个基本的概念:任何事物都有状态。状态可以是任何东西,如温度,电池状态等越简单的系统越便宜,开发更迅速,包含更少的错误,更加强健。一种技术想要获得成功必须降低成本。服务器…...

【Java 进阶篇】Java BeanUtils 使用详解
Java中的BeanUtils是一组用于操作JavaBean的工具,它允许你在不了解JavaBean的具体内部结构的情况下,访问和修改其属性。本文将详细介绍Java BeanUtils的使用,包括如何获取和设置JavaBean的属性,复制属性,以及如何处理嵌…...
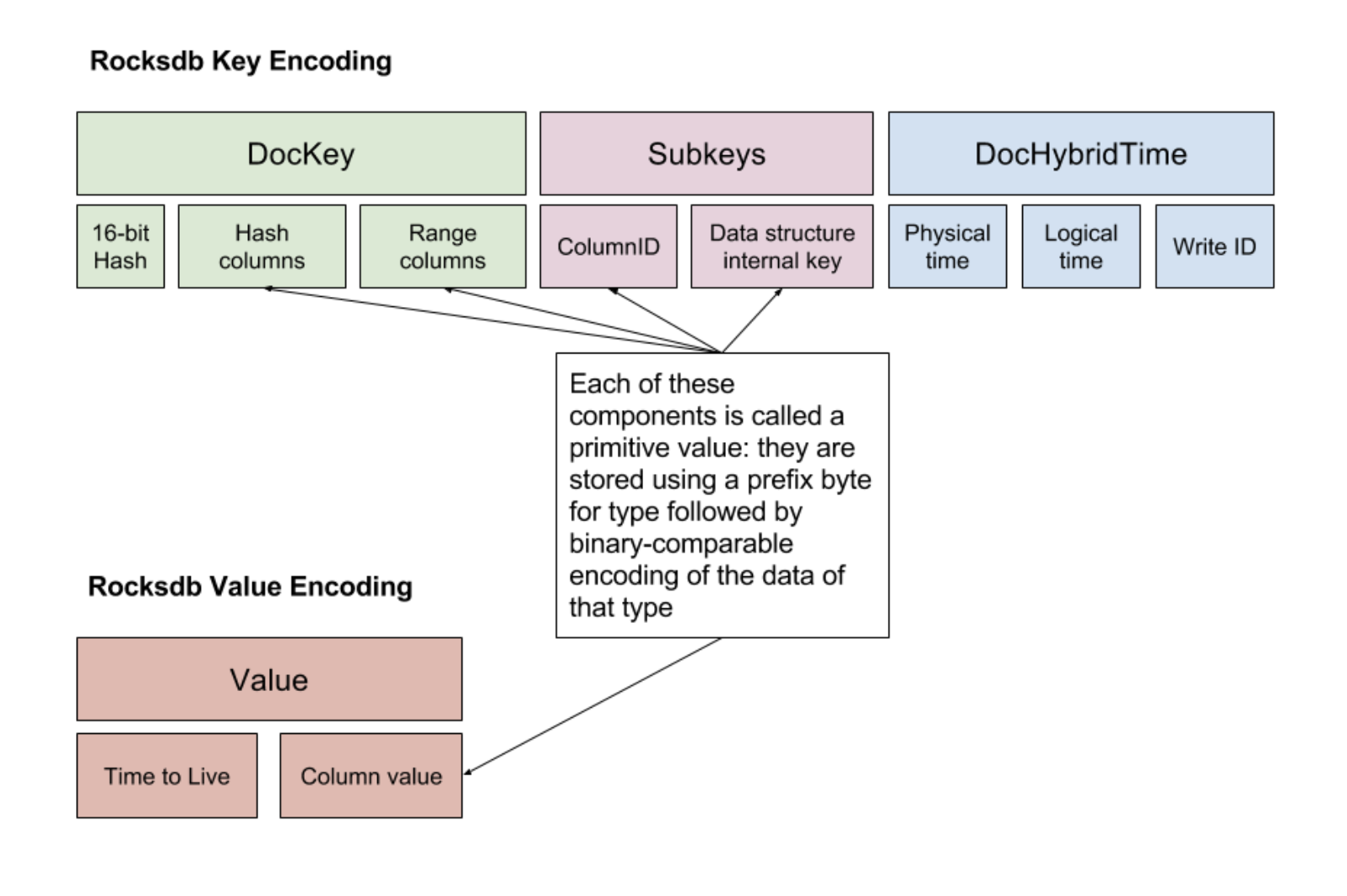
YugaByteDB -- 全新的 “PostgreSQL“ 存储层
文章目录 0 背景1 架构1.1 Master1.2 TServer1.3 Tablet 2 读写链路2.1 DDL2.2 DML2.3 事务 3 KEY 的设计4 Rocksdb 在 YB 中的一些实践总结 0 背景 YugaByteDB 的诞生也是抓住了 spanner 推行的NewSQL 浪潮的尾巴,以 PG 生态为基础 用C实现的 支持 SQL 以及 CQL 语…...

众佰诚:抖音上做生意卖什么好
随着科技的发展,越来越多的人开始利用网络平台进行创业。抖音作为目前最火的短视频平台之一,也成为了许多人选择的创业渠道。那么,在抖音上做生意卖什么好呢? 首先,我们可以考虑一些具有创新性和独特性的产品。例如,手…...

【Redis】环境配置
环境配置 Linux版本: Ubuntu 22.04.2 LTS 下载redis sudo apt install redis 启动redis redis-server 输入redis-server启动redis竟然报错了,原因是redis已经启动,网上大多数的解决方案如下: ps -ef | grep -i redis 查询redi…...

设计交换机原理图前应先理清的框图
一、系统布局图 需重点考虑“外壳、电源、风扇、主板(包含MAC、CPU、PHY)、指示灯、管理网口/串口、电口/光口等连接器”在整机中的大致位置,在系统布局图中予以体现。 二、系统框图 (1)电源整体框图; &…...
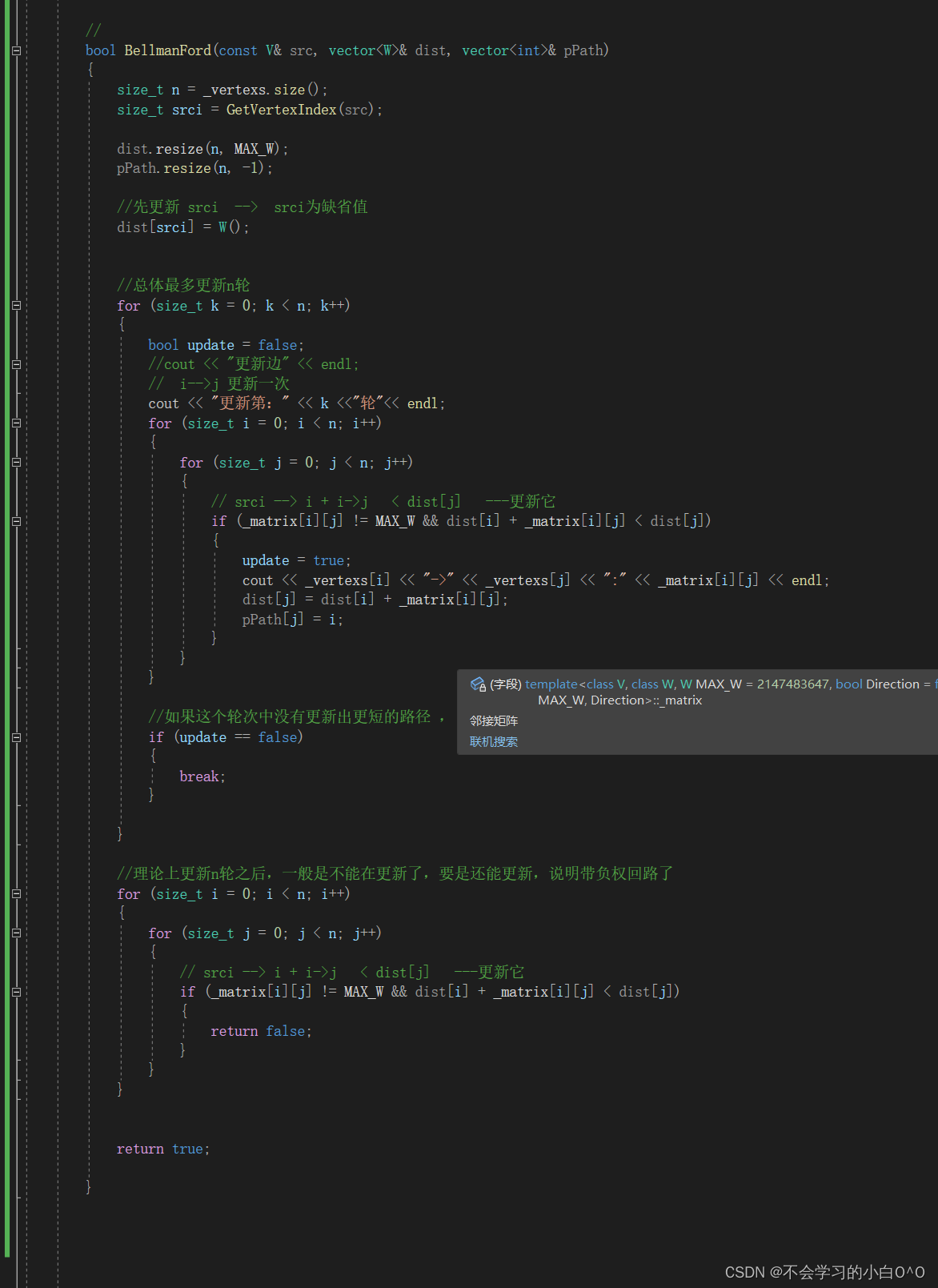
Bellman-ford 贝尔曼-福特算法
Bellman-ford算法可以解决负权图的单源最短路径问题 --- 它的优点是可以解决有负权边的单源最短路径问题,而且可以判断是否负权回路 它也有明显的缺点,它的时间复杂度O(N*E)(N是点数 , E是边数)…...

Docker数据目录迁移解决方案
前置工作 使用以下命令查询当前docker数据目录安装路径: docker info | grep "Docker Root Dir"下文以 /home/rain/docker 这个路径作为要迁移的新 Docker 安装(存储)目录 迁移方案 方法一:软链接 停掉Docker服务: systemctl…...

公共字段自动填充、菜品管理
一、公共字段填充 1.1、问题分析 1.2、实现思路 1.3、代码开发 1.3.1、自定义注解 import com.sky.enumeration.OperationType;import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import jav…...
前端面试 面试多起来了
就在昨天 10.17 号,同时收到了三个同学面试的消息。他们的基本情况都是双非院校本科、没有实习经历、不会消息中间件和 Spring Cloud 微服务,做的都是单体项目。但他们投递简历还算积极,从今年 9 月初就开始投递简历了,到现在也有一个多月了。 来看看,这些消息。 为…...
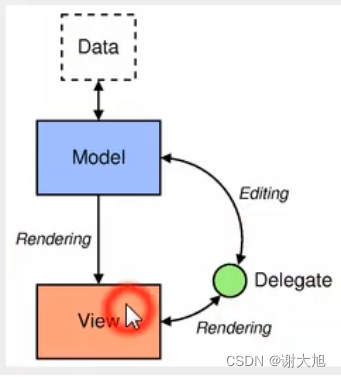
Qt常见类名关系整理
1、QAbstractItemModel与QAbstractItemView 模型的基类: The QAbstractItemModel class provides the abstract interface for item model classes. Inherited By: QAbstractListModel,QAbstractProxyModel,and QAbstractTableModel 视图的基类: The QAbstractIte…...

YOLO8实战:yolov8实现行人跟踪计数
本篇文章首先介绍YOLOV8实现人流量跟踪计数的原理,文末附代码 引言:行人跟踪统计是智能监控系统中的重要功能,可以广泛应用于人流控制、安全监控等领域。传统的行人跟踪算法往往受到光照、遮挡等因素的干扰,难以实现准确跟踪。随着深度学习技术的发展,目标检测模型逐渐成为…...
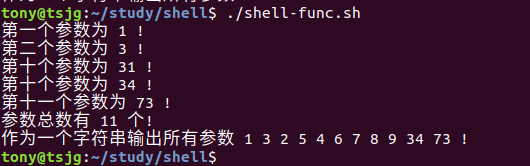
shell脚本学习-2
文章目录 一、shell参数传递二、shell中的特殊变量三、shell中的函数四、shell函数中的参数 一、shell参数传递 运行 Shell 脚本文件时我们可以给它传递一些参数,这些参数在脚本文件内部可以使用$n的形式来接收,例如,$1 表示第一个参数&…...

web3:智能合约浏览器版本的 IDE - remix 使用教程
如果你是一位web3行业的从业者,那么智能合约一定是要接触的,这里我们就智能合约浏览器版本的 IDE-remix来介绍一下,及简单的使用操作 目录 Remix简介官方网址语言设置使用编辑合约编译合约部署合约测试验证Remix简介 Remix 是一个开源的 Solidity 智能合约开发环境,是一款…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
