回归算法|长短期记忆网络LSTM及其优化实现
本期文章将介绍LSTM的原理及其优化实现
序列数据有一个特点,即“没有曾经的过去则不存在当前的现状”,这类数据以时间为纽带,将无数个历史事件串联,构成了当前状态,这种时间构筑起来的事件前后依赖关系称其为时间依赖,利用这类依赖关系进行建模是对其进行学习的关键。
近年来,越来越多的神经网络模型被用于序列数据的预测,如股票、电力负荷、风电功率、心电信号等场景,并取得了不错的效果。
通常,神经网络模型可以分为两类:
一类是以BP神经网络为代表的神经网络,这类网络结构简单,但容易出现陷入局部极值、过拟合等问题,并且其并没有对于依赖关系进行利用;
另一类是更深层次、更高效的深度神经网络模型,如CNN、RNN、LSTM,这类网络是较为前沿和高效的预测模型,其能够拟合输入变量间的非线性复杂关系,并且对于RNN和LSTM来说,其能够克服传统神经网络没有记忆功能的问题,可以有效的根据历史信息进行学习和预测。相对于RNN,LSTM能避免RNN在长序列数据中出现的梯度消失或爆炸的问题,是最为流行的RNN(LSTM是在RNN基础上的改进),因此LSTM在序列数据学习中得到了广泛应用。
LSTM同样面临着隐含层神经元个数、学习率、迭代次数等超参数设置的问题,这些参数都将影响LSTM的预测精度,利用优化算法进行超参数的寻优比经验法更为科学高效,因此本文将详细介绍LSTM模型的原理及其优化实现。
00 目录
1 LSTM模型原理
2 优化算法及其改进概述
3 GWO-LSTM预测模型
4 代码目录
5 实验结果
6 源码获取
01 LSTM神经网络模型[1]
长短时记忆神经网络(LSTM)是Sepp Hochreiter和Jurgen Schmidhuber在1997年对递归神经网络(RNN)进行改进的算法。它旨在解决递归神经网络(RNN)产生的梯度消失问题,在长距离依赖任务中的表现也远好于RNN。LSTM模型的工作方式和RNN基本相同,但是LSTM模型实现了更为复杂的内部处理单元来处理上下文信息的存储与更新。
Hochreiter 等人主要引入了记忆单元和门控单元实现对历史信息和长期状态的保存,通过门控逻辑来控制信息的流动。后来Graves等人对LSTM单元进行了完善,引入了遗忘门,使得LSTM模型能够学习连续任务,并能对内部状态进行重置。
LSTM主要由三个门控逻辑(输入、遗忘和输出)实现。门控可以看作一层全连接层,LSTM对信息的存储和更新正是由这些门控来实现的。更具体地说,门控由Sigmoid函数和点乘运算实现。
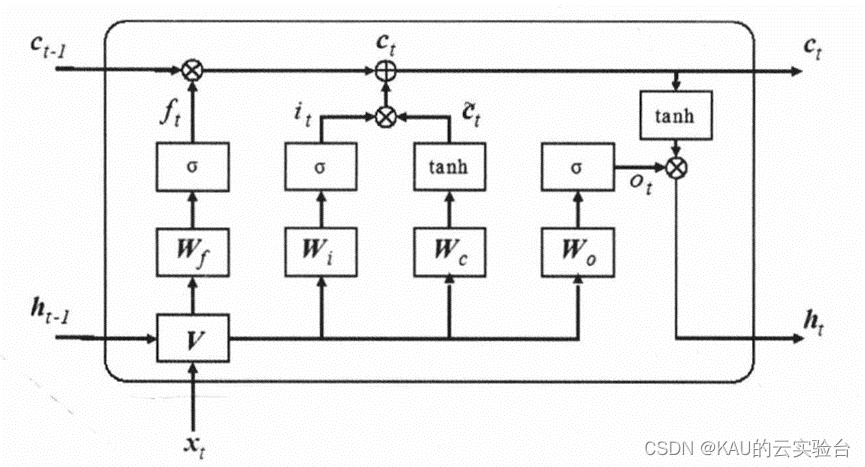
这里分别使用i、f、o来表示输入门、遗忘门和输出门,O表示对应元素相乘,W和b分别表示网络的权重矩阵与偏置向量。在时间步为t时,LSTM隐含层的输入与输出向量分别为x,和h,,记忆单元为c,,输入门用于控制网络当前输入数据x,流入记忆单元的多少,即有多少可以保存到c,,其值为:
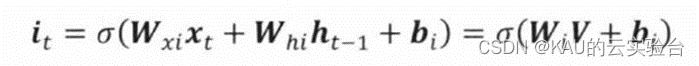
遗忘门是LSTM 的关键组成部分,可以控制哪些信息要保留哪些要遗忘,并且以某种方式避免当梯度随时间反向传播时引发的梯度消失和爆炸问题。遗忘门可以决定历史信息中的哪些信息会被丢弃,即判断上一时刻记忆单元ct-1中的信息对当前记忆单元ct的影响程度。
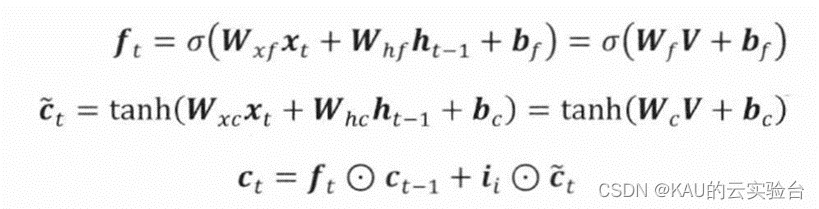
输出门控制记忆单元c,对当前输出值h,的影响,即记忆单元中的哪一部分会在时间步t输出。输出门的值及隐含层的输出值可表示为:
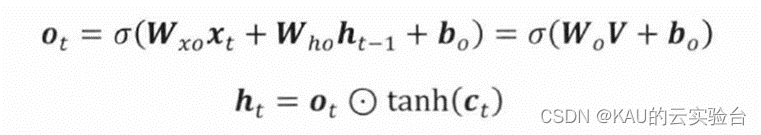
02 优化算法及其改进概述
前面的文章中作者介绍了许多种优化算法及其改进算法,
这里我们以灰狼优化算法为例,其他算法同理。作者的代码很多都是标准化的,其他文章里的算法替换起来也很容易。
03 GWO-LSTM预测模型
超参数在一定程度上会影响LSTM网络的拟合精度,因此必须获得适合不同特征数据的最佳超参数值。然而,目前还没有成熟的理论来获得合适的超参数值。因此,本文采用灰狼优化算法,得到LSTM的最佳网络超参数值,包括初始学习率、隐含层神经元数、批次大小和训练迭代次数,即[lr,L1,L2,Batch,k]。其中增加隐藏层数可提高模型的非线性拟合能力,但同时也使模型更复杂,预测时间随之增加,甚至引发过拟合问题﹐因此本文将隐藏层数选择的范围控制在2层。优化参数的约束条件设置如下:
以MSE作为适应度,GWO-LSTM预测模型的流程图如下: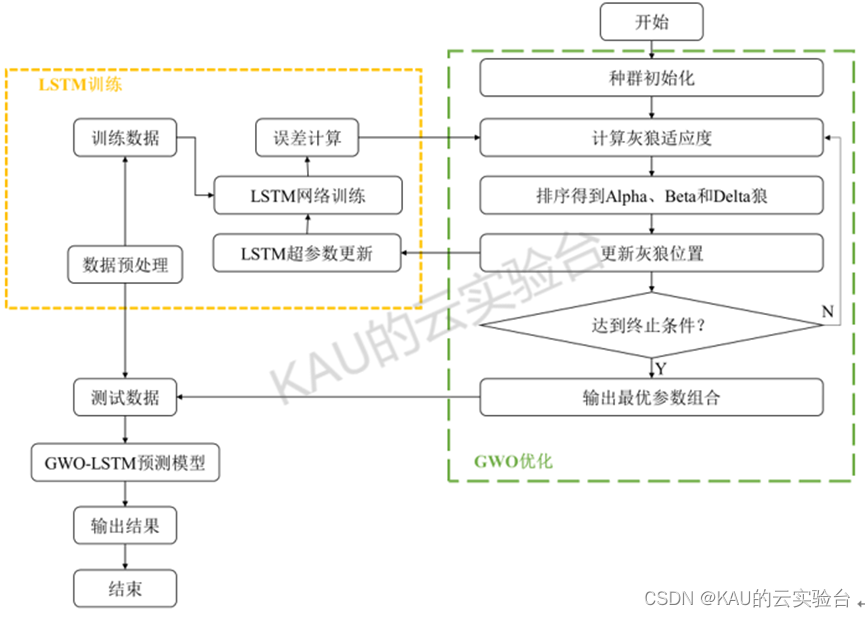
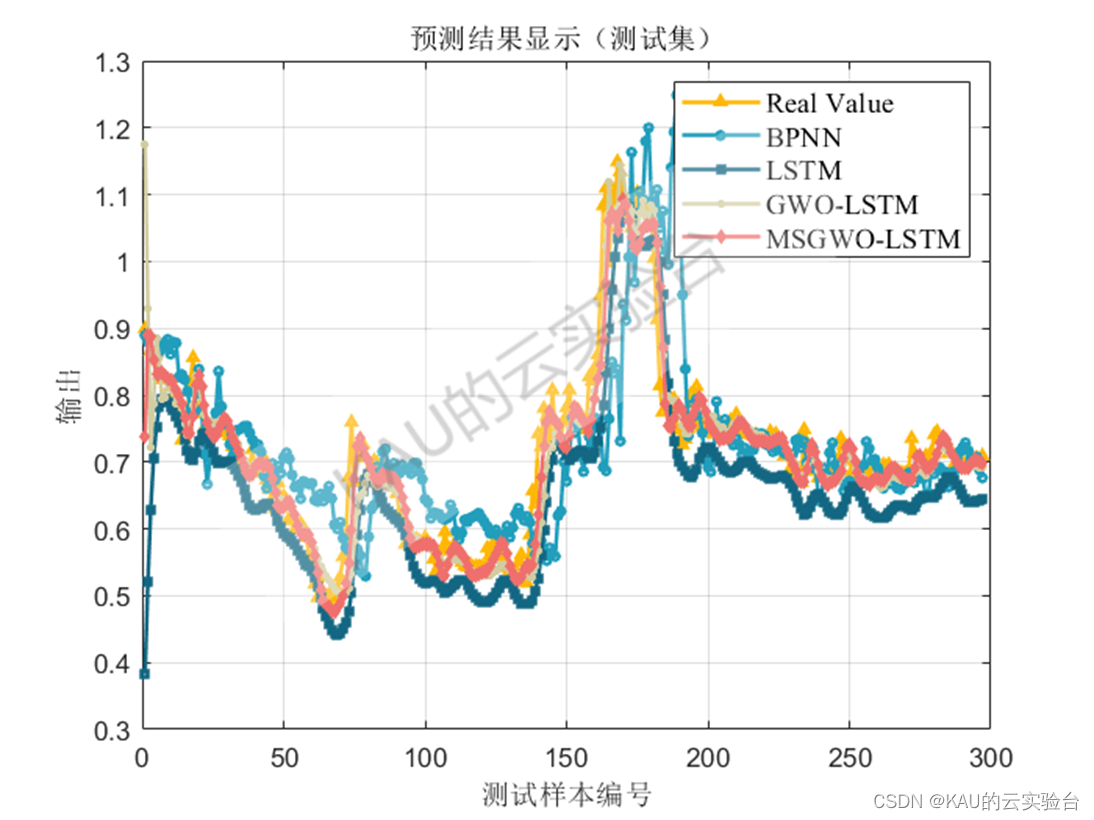
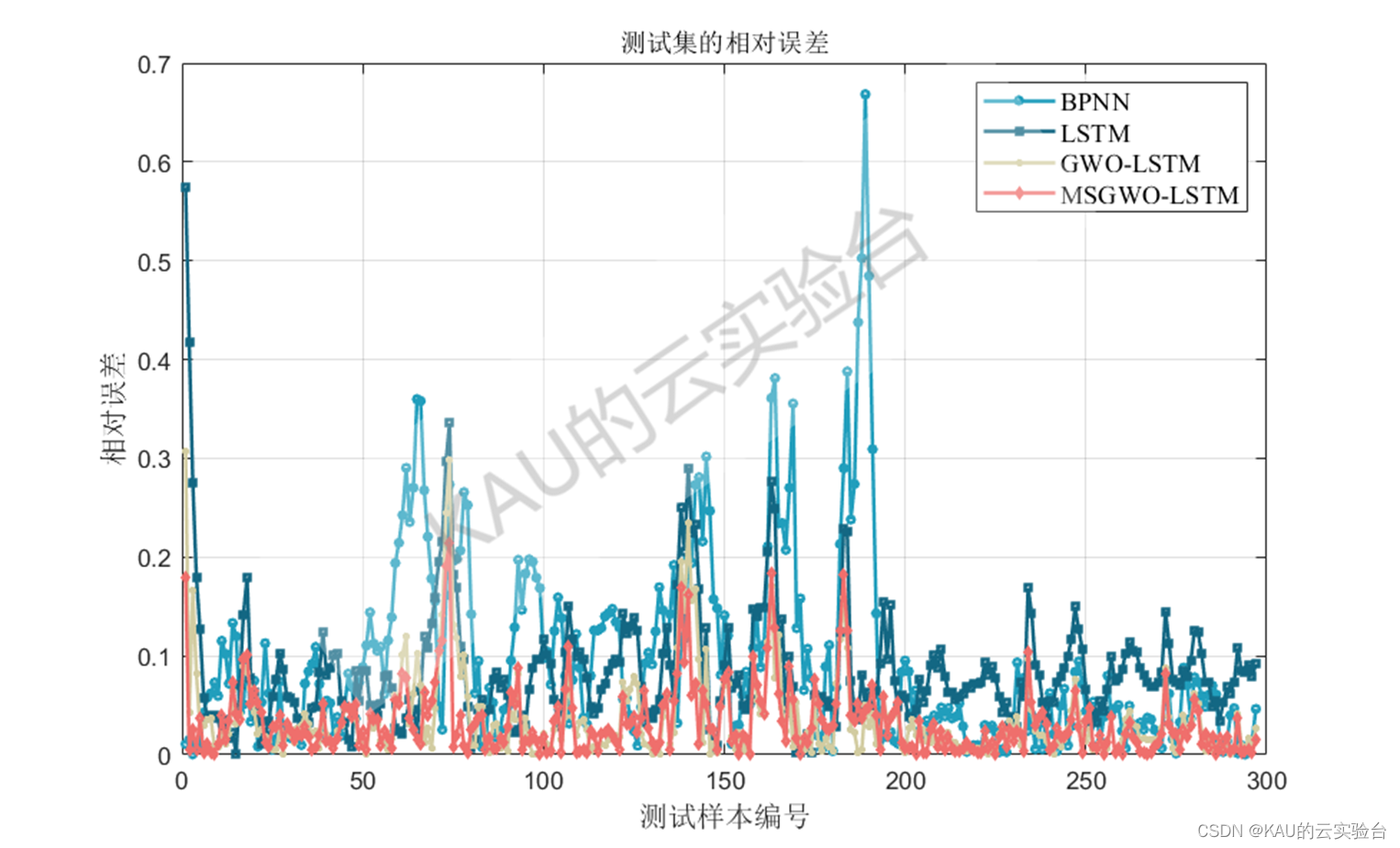
04 实验结果
以均方根差(Root Mean Square Error,RMSE) 、平均绝对百分误差( Mean Absolute Percentage Error,MAPE) 、平均绝对值误差 ( Mean Absolute Error,MAE) 和可决系数(coefficient of determination,R^2)作为序列数据拟合的评价标准。
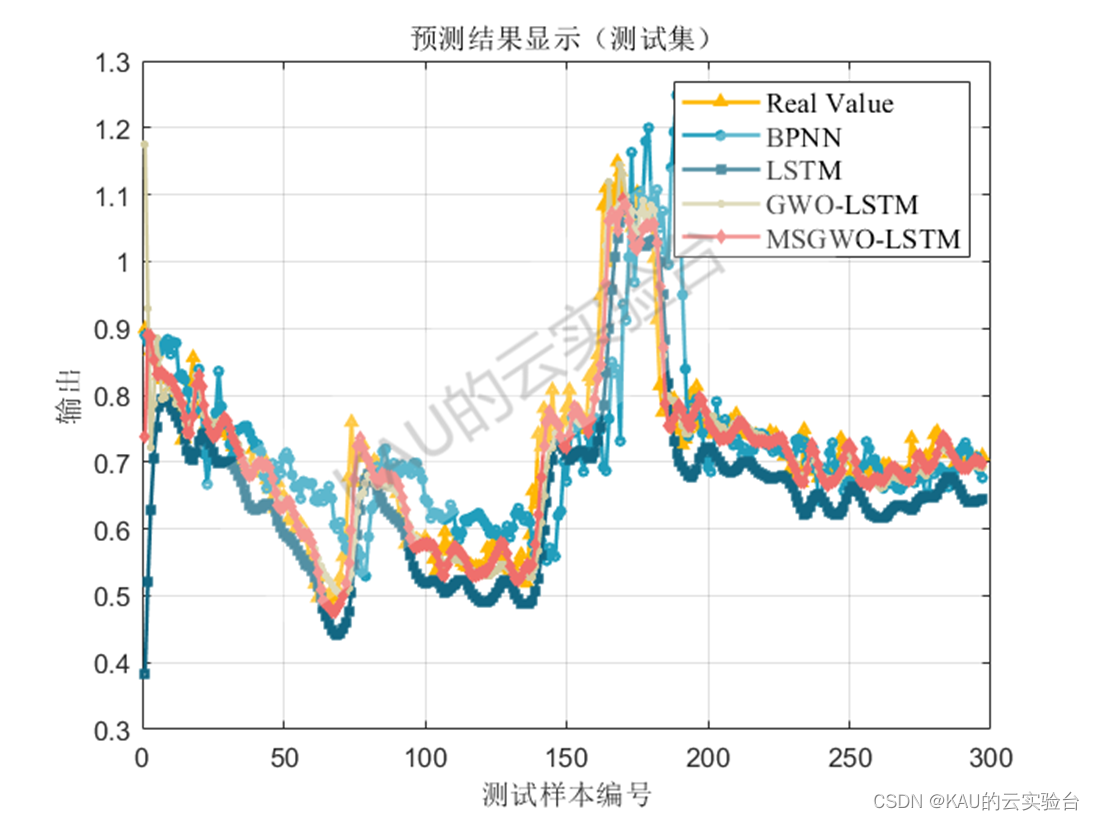
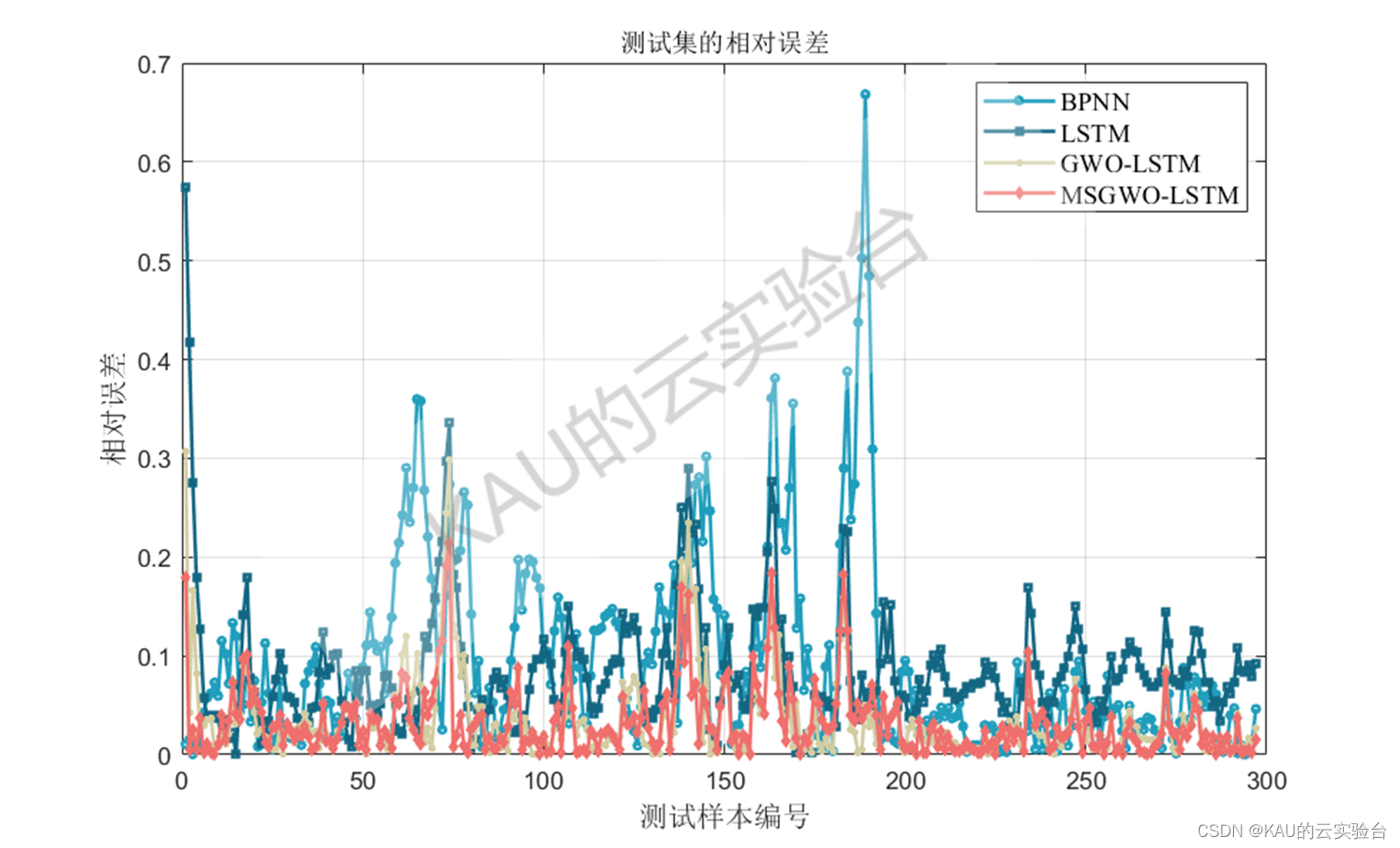
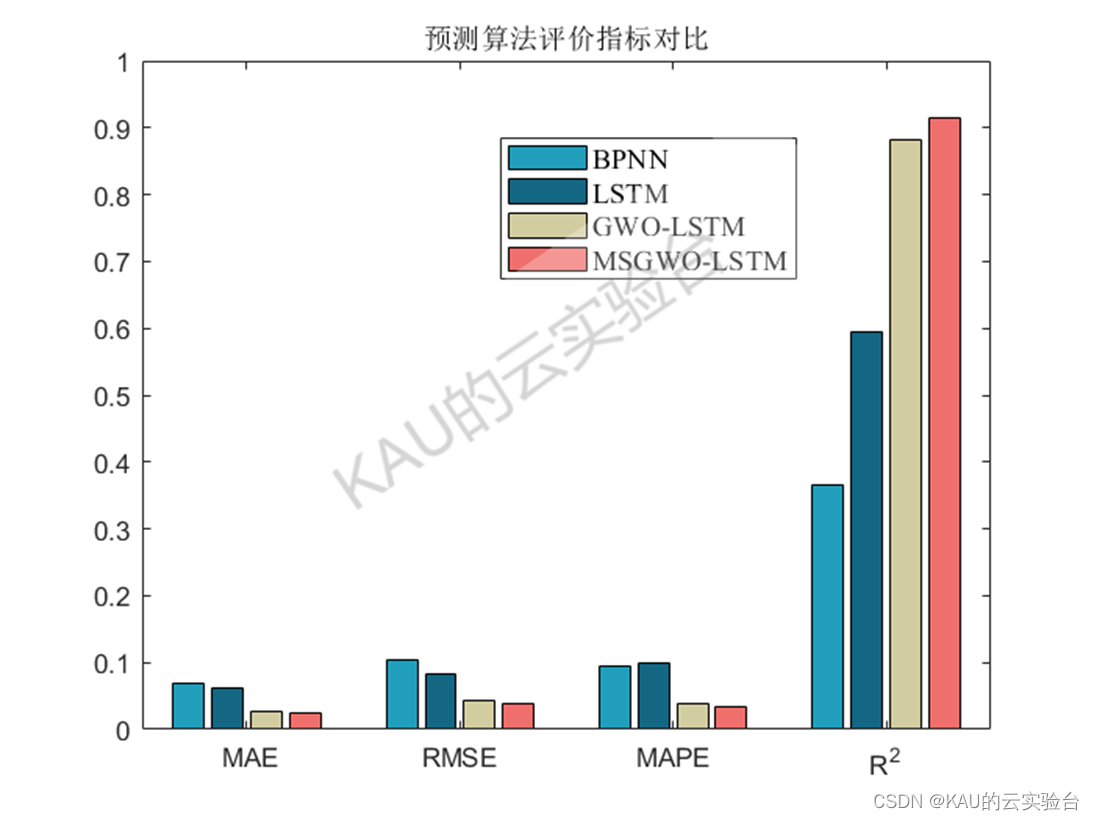
图中MSGWO为作者前面改进的灰狼优化算法
05 源码获取
代码注释详细,一般只需要替换数据集就行了,注意数据的行是样本,列是变量,源码提供3个版本
1.免费版
其主要是LSTM预测模型,包含Matlab和Python的程序,对于需要进行一些简单预测或者是想学习LSTM算法的同学足够了。

获取方式——GZH(KAU的云实验台)后台回复:LSTM
2.付费版1
主要是GWO优化LSTM的预测模型,这个只包含了Matlab程序,包括BP、LSTM、GWO-LSTM的预测对比。因为最近比较忙,Python就没有出,程序的注释详细,易于替换,卡卡之前介绍过的智能优化算法都可以进行替换。
获取方式——GZH后台回复:GWOLSTM
3.付费版2
主要是MSGWO优化LSTM的预测模型,这个只包含了Matlab程序,包括BP、LSTM、GWO-LSTM、MSGWO-LSTM的预测对比,也即在结果展示中的图片,其中MSGWO即为卡卡前面的融合多策略的改进灰狼优化算法的文章,程序的注释详细,这部分程序包含了函数测试、预测模型两个部分,可以用来发这类方向的文章,当然你也可以在卡卡算法的基础上再作创新改进,比如预测模型上可以再对预测误差做一个预测模型进行级联,或者对改进的灰狼算法再引入别的修改策略等等。
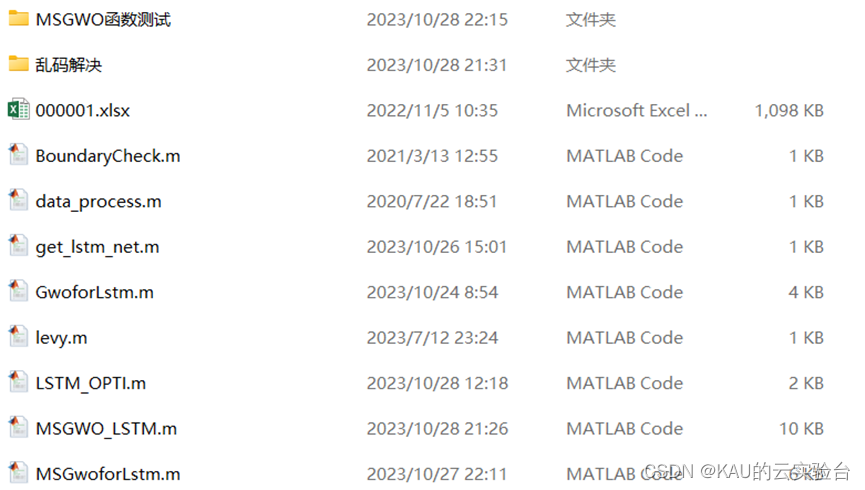
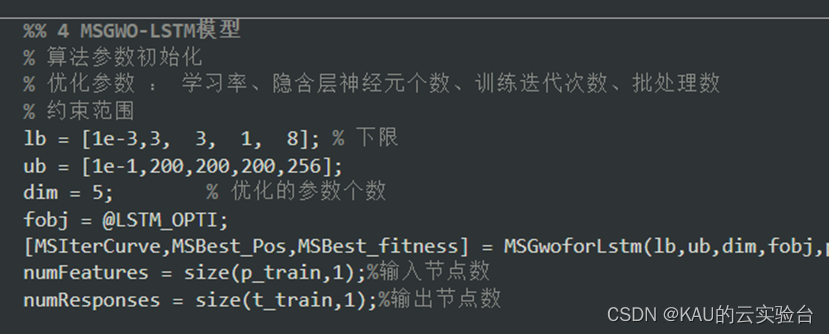
获取方式——GZH后台回复:MSGWOLSTM
[1]游皓麟著.Python预测之美:数据分析与算法实战[M] .电子工业出版社
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行)。
相关文章:

回归算法|长短期记忆网络LSTM及其优化实现
本期文章将介绍LSTM的原理及其优化实现 序列数据有一个特点,即“没有曾经的过去则不存在当前的现状”,这类数据以时间为纽带,将无数个历史事件串联,构成了当前状态,这种时间构筑起来的事件前后依赖关系称其为时间依赖&…...
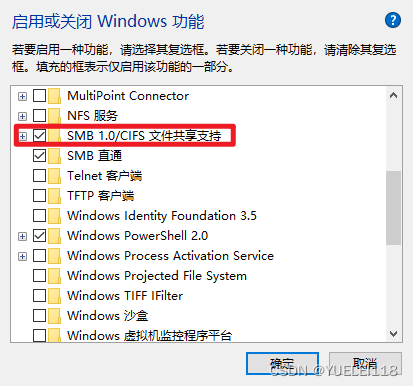
小米电视播放win10视频 win10共享问题
解决的方法就是安装SMB1.0协议 重启就OK了...

uniApp开发注意要点提炼-xyphf
我们在使用uniApp开发的时候,很多朋友由于对多端兼容性的不了解,结果在多端编译的时候经常出这样或者那样的问题,而不断的说uniApp这坑那坑的,下面我基于自身经验和官网说明提炼一些常见的注意要点。 因为很多公司时常初衷是开发一…...

DHorse改用fabric8的SDK与k8s集群交互
现状 在dhorse 1.4.0版本之前,一直使用k8s官方提供的sdk与k8s集群交互,官方sdk的Maven坐标如下: <dependency><groupId>io.kubernetes</groupId><artifactId>client-java</artifactId><version>18.0.0…...

如何在阿里云国际站服务器上添加IP白名单?
跟着云核算的发展,越来越多的企业和个人开始使用阿里云服务器。为了确保服务器的安全,咱们需要在阿里云服务器上增加IP白名单。这篇文章将具体解说如何在阿里云服务器上增加IP白名单。 增加IP白名单是保证服务器安全的重要手法之一。通过增加IP白名单&am…...

GPT实战系列-ChatGLM2模型的微调训练参数解读
GPT实战系列-ChatGLM2模型的微调训练参数解读 目录 GPT实战系列-ChatGLM2模型的微调训练参数解读ChatGLM2模型1、P-Tuning模型微调2、微调训练配置参数train.sh中配置参数训练配置信息模型配置信息附录:训练正常运行打印信息 ChatGLM2模型 ChatGLM-6B是开源的文本生…...
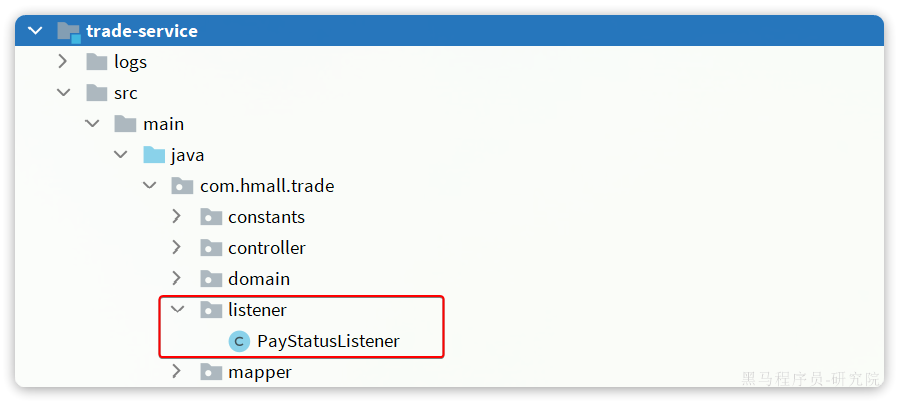
RabbitMQ入门到实战教程,消息队列实战,改造配置MQ
RabbitMQ入门到实战教程,MQ消息中间件,消息队列实战-CSDN博客 3.7.Topic交换机 3.7.1.说明 Topic类型的Exchange与Direct相比,都是可以根据RoutingKey把消息路由到不同的队列。 只不过Topic类型Exchange可以让队列在绑定BindingKey 的时候…...
phar反序列化学习
PHP反序列化常见的是使用unserilize()进行反序列化,除此之外还有其它的反序列化方法,不需要用到unserilize()。就是用到phar反序列化。 Phar phar文件 Phar是将php文件打包而成的一种压缩文档,类似于Java中的jar包。它有一个特性就是phar文…...
十年回望 -- JAVA
十年 十年时间,弹指一挥,好像一直都是在为工作奔波,匆匆忙忙的十年。 一、个人介绍 本人毕业于一所很普通的公办专科院校(全日制统招大专),专业是软件技术,当初能进入计算机这一行业࿰…...

Linux 环境下 安装 Elasticsearch 7.13.2
Linux 环境下 安装 Elasticsearch 7.13.2 前言镜像下载(国内镜像地址)解压安装包修改配置文件用 Es 自带Jdk 运行配置 Es 可被远程访问然后启动接着启动本地测试一下能不能连 Es 前言 借公司的 centos 7 服务器,搭建一个 Es,正好熟…...
心理咨询预约小程序
随着微信小程序的日益普及,越来越多的人开始关注如何利用小程序来提供便捷的服务。对于心理咨询行业来说,搭建一个心理咨询预约小程序可以大大提高服务的效率和用户体验。本文以乔拓云平台为例,详细介绍如何轻松搭建一个心理咨询预约小程序。…...

常用排序算法的理解
1.插入排序 插入排序的思想是将一个记录插入到已经排好序的有序表中,从而形成一个新的、记录数加1的有序表。在其实现过程使用双层循环,外层循环是进行插入的次数(也可以理解为比较的轮数),内层循环是当前记录查找插入…...

Python小程序 - 文件解析
1. 目录下文件解析:特定文件、文件列表、文件数 Windows文件目录分格使用“ / ” 或 “ \\ ”文件目录路径包含空格的,绝对路径使用“双引号”,保证文件路径的可识别性保存和读取结果时,使用 encodingUTF-8可以添加对文件目录的过…...

.mxdown-V-XXXXXXXX勒索病毒的最新威胁:如何恢复您的数据?
导言: 在数字时代,网络安全威胁层出不穷,其中.mxdown-V-XXXXXXXX、.vollhavhelp-V-XXXXXXXX、.arricklu-V-XXXXXXXX勒索病毒已成为备受关注的问题。这种病毒以其高级加密技术和威胁勒索金的方式,严重危害用户和企业的数据安全。本…...

audio 标签动态src 且src是http无法播放问题
<audioref"audio" :src"src"alt"加载失败"controls/>src是动态传参的 无法播放因为动态src需要在赋值后对audio进行重载 this.$refs.audio.load()注意如果,src跟本项目地址IP端口协议不同,会出现跨域问题。audio标…...

Leetcode—485.最大连续1的个数【中等】明天修改
2023每日刷题(十五) Leetcode—2.两数相加 迭代法实现代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l…...
JavaWeb 怎么在servlet向页面输出Html元素?
service()方法里面的方法体: resp.setContentType("text/html;charsetutf-8");//获得输出流PrintWriter对象PrintWriter outresp.getWriter();out.println("<html>");out.println("<head><title>a servlet</title>…...
Spring及SpringBoot中AOP的使用
Spring中AOP示例 <dependencies><!--Spring核心包--><dependency><groupId>org.springframework</groupId><artifactId>spring-core</artifactId><version>5.3.6</version></dependency><!--引入SpringBean--&…...
cmake多目录构建初步成功
目录和代码和 首次cmake 多目录构建失败 此文一样; 只有一个CMakeLists.txt; cmake_minimum_required(VERSION 3.10) project(mytest3 VERSION 1.0) include_directories("${PROJECT_SOURCE_DIR}/include") add_executable(mytest3 src/main…...
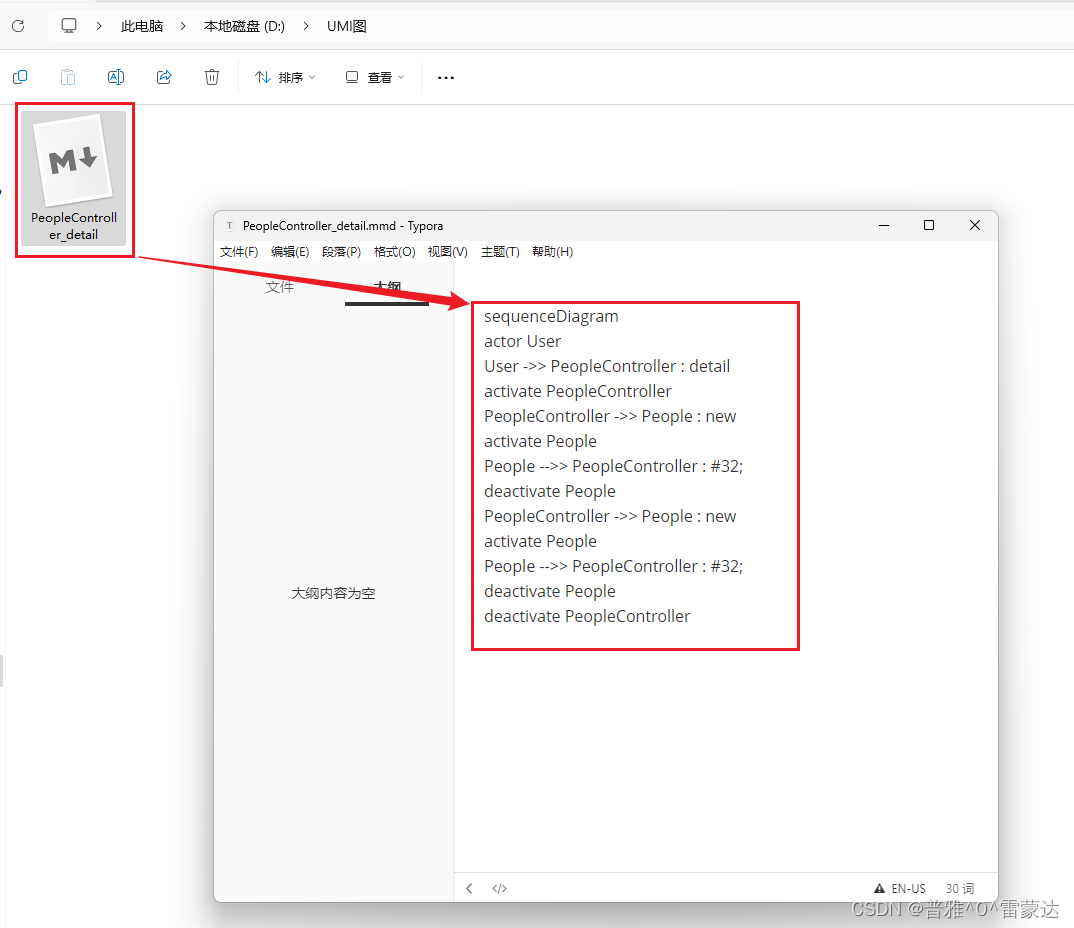
idea插件(一)-- SequenceDiagram(UML自动生成工具)
目录 1. 安装 2. 默认快捷键 3. 操作说明 4. 导出为图片与UML类图 4.1 导出为图片: 4.2 导出 UML 类图 SequenceDiagram是从java、kotlin、scala(Beta)和groovy(limited)代码生成简单序列图(UML&…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
