647. 回文子串 516. 最长回文子序列
647. 回文子串
方法一:动态规划
dp[i][j]:[i,j]范围的下标字符串s是否为回文子串
遍历字符串,每次判断s[i]与s[j]是否相等
①若相等,j-i=0 即单个字符串s[i],那么一定为回文子串,赋值为1
②若相等,j-i=1 即两个相同字符串,那么也一定为回文子串,赋值为1
③若相等,j-i>1 子串的长度大于2,那么就要判断子串内侧的子串是否为回文子串,若是,则该子串为回文子串 即dp[i][j]=dp[i+1][j-1]
若不相等,则不为回文子串,dp值默认为0
遍历顺序,i取决于i+1,i从下len往上0遍历,j取决于j-1,从左i往右len遍历。
因此先遍历最后一个字符。
方法二:双指针法
中心扩散法,i从前向后遍历
①每次以i为中心向左右扩散,若s[start]=s[end]则为一个回文串 (start=end=i)
②每次以[i,i+1]为中心向左右扩散,若s[start]=s[end]则为一个回文串(start=i,end=i+1)
while (start >= 0 && end < size && s.charAt(start) == s.charAt(end)) {start--;end++;res++;}516. 最长回文子序列
dp[i][j]:[i,j]范围内的s子串下标回文子串的长度
若s[i]=s[j],长度为[i+1,j-1]最长回文子串长度+2
否则不是回文子串,长度为[i+1,j]和[i,j+1]的最长回文子串长度 的较大值。
i取决于i+1,从下往上遍历,j取决j+1,从前往后遍历。
初始化dp[i][i]=1 即单个字符长度为1
i从len-1开始向前遍历,j从i+1开始向后遍历。
最后返回最后遍历的dp[0][len-1]的值即为该字符串最长回文子串长度
相关文章:

647. 回文子串 516. 最长回文子序列
647. 回文子串 方法一:动态规划 dp[i][j]:[i,j]范围的下标字符串s是否为回文子串 遍历字符串,每次判断s[i]与s[j]是否相等 ①若相等,j-i0 即单个字符串s[i],那么一定为回文子串,赋值为1 ②若相等,j-i1…...

实用小妙招
记录一些实用小妙招,都是收藏夹里收藏的各种文章,总结在一起,持续更新 实用小妙招LinuxUbuntu修改终端语言安装 Node.js (nvm)git 记住账号密码WSL迁移默认用户修改Linux Ubuntu 修改终端语言 apt update apt install -y language-pack-zh…...

别让猴子跳回背上
1.管理者的贡献来自于他们的判断力与影响力,而非他们所投入的个人时间与埋头苦干 2.管理者的绩效表现则是许多人群策群力的结果 3.管理者的时间管理: 老板占用的时间;组织占用的时间;自己占用的时间;外界占用的时间; 4.管理者的策略在于增加自己的时间,…...
数据结构 | 线性表
🔥Go for it!🔥 📝个人主页:按键难防 📫 如果文章知识点有错误的地方,请指正!和大家一起学习,一起进步👀 📖系列专栏:数据结构与算法 ὒ…...

Deepwalk深度游走算法
主要思想 Deepwalk是一种将随机游走和word2vec两种算法相结合的图结构数据的挖掘算法。该算法可以学习网络的隐藏信息,能够将图中的节点表示为一个包含潜在信息的向量, Deepwalk算法 该算法主要分为随机游走和生成表示向量两个部分,首先…...
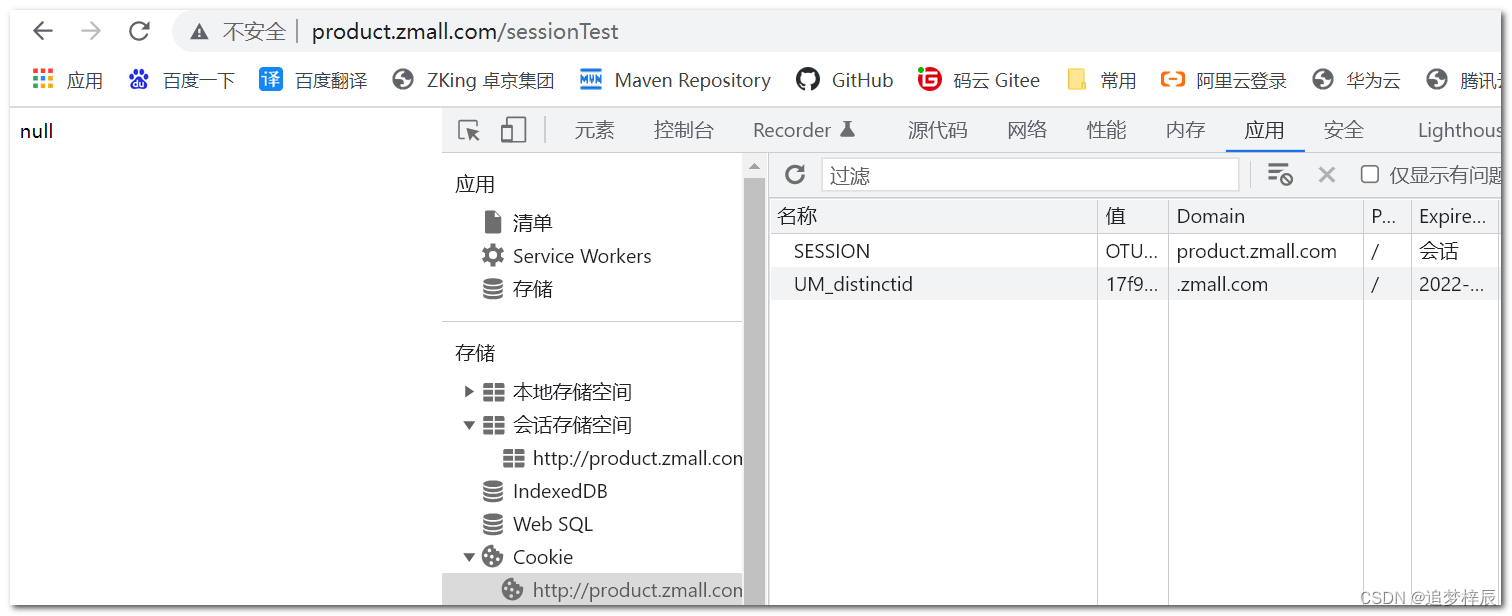
微服务项目【服务调用分布式session共享】
nginx动静分离 第1步:通过SwitchHosts新增二级域名:images.zmall.com 第2步:将本次项目的所有静态资源js/css/images复制到nginx中的html目录下 第3步:在nginx的核心配置文件nginx.conf中新增二级域名images.zmall.com访问映射…...

神经网络的万能逼近定理
这是我见过的讨论神经网络万有逼近问题的最好的文章。在文章中,给出了最清晰,简洁的构造性证明。揭示了它的本质。 三十年前,我们接触到神经网络的万有逼近问题。发表了几篇文章。这些文章把神经网络能力的来历、优点、缺点,都已…...

【信息系统项目管理师】项目管理过程的三万字大论文
【信息系统项目管理师】项目管理过程的三万字大论文 【信息系统项目管理师】项目管理过程的三万字大论文 【信息系统项目管理师】项目管理过程的三万字大论文1.制定项目章程2.识别干系人3.制定范围管理计划4.制定进度管理计划5.制定成本管理计划6.制定质量管理计划7.编制人力资…...

【C++】C++11 ~ 包装器解析
🌈欢迎来到C专栏~~包装器解析 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&a…...

SpringBoot整合(三)SpringBoot发送邮件
使用SpringBoot发送邮件 邮件发送其实是一个非常常见的需求,用户注册,找回密码等地方,都会用到,Spring Boot 中对于邮件发送,提供了相关的自动化配置类,使得邮件发送变得非常容易。 1、前置工作 目前国内…...
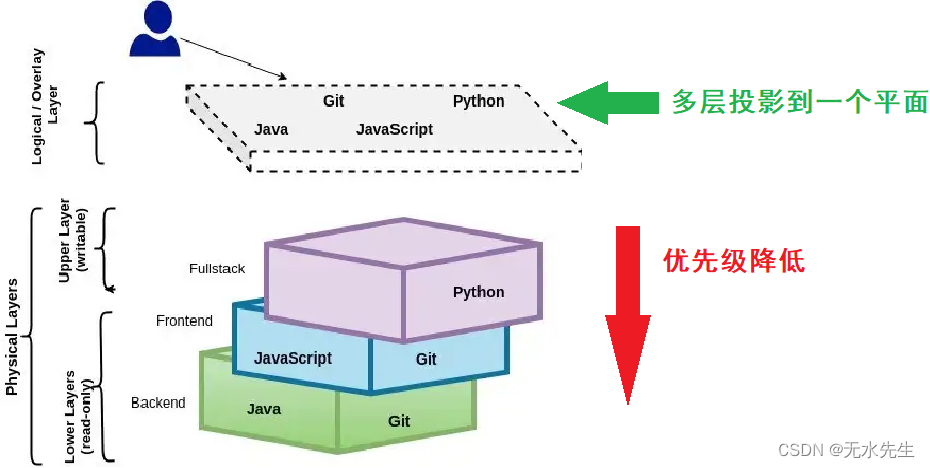
【docker知识】联合文件系统(unionFS)原理
一、说明 Docker CLI 操作起来比较简单——您只需掌握Create、Run、InspPull和Push容器和图像,但是谁想过Docker 背后的内部机制是如何工作的?在这个简单的表象背后隐藏着许多很酷的技术, UnionFS(统一文件系统)就是其…...
使用Lame库实现wav、pcm转mp3
文章目录 前言 一、Lame库是什么? 二、使用步骤 0.创建native项目 1.下载Lame库 2.pcm转MP3 3.wav转MP3 4、native方法如下 三、注意 总结 前言 因为使用android录音后生成的文件是wav或者pcm格式,项目要求最后的文件需要是mp3格式,于…...

c++11 标准模板(STL)(std::multimap)(三)
定义于头文件 <map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class multimap;(1)namespace pmr { template <class Key, class T…...

【报复性赚钱】2023年5大风口行业
今天就来和大家分享一下,在时代的洪流下,普通人如何顺应大势抓住机遇! 实现人在风口上,猪都会飞起来。 根据对市场的观察及各平台数据分析结果,结合国家政策和经济专家的分析,小编预测了2023年将会迎来大…...

单目相机、双目相机和RGB-D相机学习笔记(一些视频和博文网址)
目录1. 单目相机1.1 摄像头原理1.2 单目相机的标定2 双目相机2.1 双目相机定位原理2.2 双目相机的缺陷3 RGB-D相机3.1 深度相机结构光原理3.2 RGB-D相机的应用1. 单目相机 1.1 摄像头原理 视频网址:【全网最详细】摄像头原理分析(约25分钟课程…...
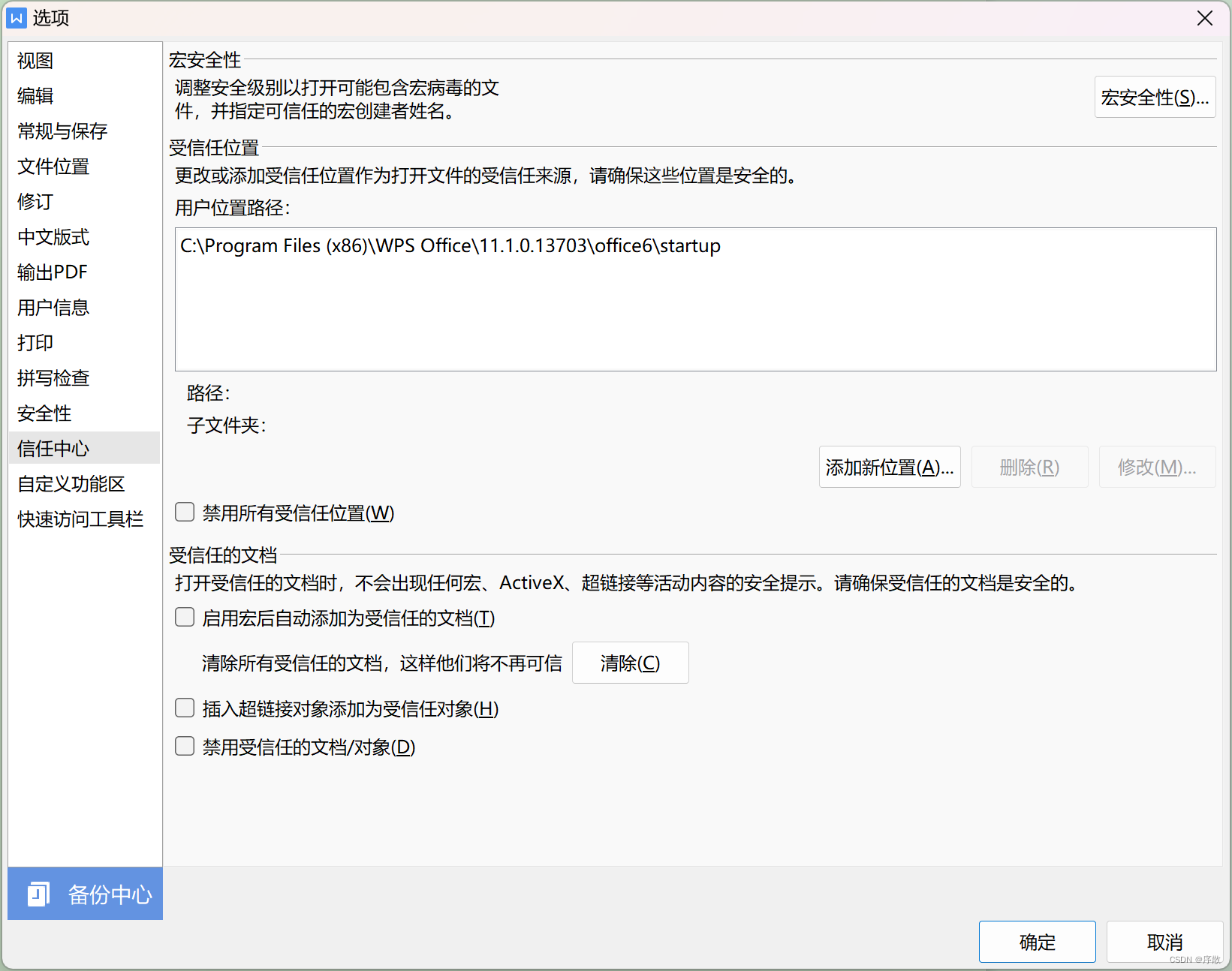
word和wps添加mathtype选项卡
word或wps添加mathtype选项卡 前提 安装好word或wps安装好mathtype 步骤 确认word或wps具体安装位置确认word或wps位数为32位还是64位复制mathtype中的MathPage.wll文件和MathType Commands 2016.dotm文件到STARTUP位置添加受信任位置添加加载项 安装位置 通过开始页面&a…...
获取成员userID
文章目录一、简介二、获取token1、获取秘钥2、获取Token三、获取部门数据1、获取部门列表2、获取子部门ID列表3、获取单个部门详情四、获取成员信息1、读取成员2、获取部门成员3、获取部门成员详情一、简介 同步数据到企微: 企业如果需要从自有的系统同步通讯录到…...

DOM编程-显示网页时钟
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>显示网页时钟</title> </head> <body bgcolor"antiquewhite"> <script type"text/javascrip…...

浅谈保护数据的加密策略
加密是一种将信息从可读格式转换为混乱字符串的技术。这样做可以防止数据传输中的机密数据泄露。文档、文件、消息和所有其他形式的网络通信都可以加密。加密策略和身份验证服务的结合,还能保障企业机密信息只对授权用户开启访问权限。常见的数据加密包括以下两种&a…...

Java中String,StringBuffer和StringBuilder
String类 我们在定义string变量时 常常写 String str "hello word"; 这样的代码,看起来和int a 0; 是一样的声明方式, 但其实两者是不同的, int 是java中定义的基本数据类型, 而String是一个类,是一个特殊的类,可以像基本数据类型一样直接赋…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
