4.OCR文本识别Connectionist Temporal Classification(CTC)算法
文章目录
- 1.基础介绍
- 2.Connectionist Temporal Classification(CTC)算法
- 2.1 什么是Temporal Classification
- 2.2 CTC问题描述
- 2.2关于对齐
- 2.3 前向后向算法
- 2.4 推理时
- 3.pytorch中的CTCLOSS
- 参考资料
欢迎访问个人网络日志🌹🌹知行空间🌹🌹
1.基础介绍
论文:Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks
这是2006年第23次ICML会以上的一篇论文。
很多实际应用需要从未切分的数据中输出序列信息,如语音识别中的语音转文字,光学字符识别(Optical character recognition,OCR)中的字符图片转字符序列。循环神经网络(Recurrent neural networks,RNN)十分适合序列数据的学习,但其训练数据要求必须是切分后的序列,而实际应用中切分的训练序列数据标注比较困难,是很难获取的。

上图是OCR的两种模型,一种如图(a)可直接输入OCR检测得到的图片得到图片中的字符串can,另外一种需要先将图片按字符进行切割,这种方式比较数据处理比较复杂,而这种正是循环神经网络RNN要求的输入。
为了充分利用循环神经网络RNN处理序列数据的能力,同时避免对输入序列图像进行切分,本文作者提出了Connectionist Temporal Classificatio(CTC)算法。
2.Connectionist Temporal Classification(CTC)算法
2.1 什么是Temporal Classification
SSS是从分布DX×Z\mathcal{D}_{\mathcal{X}\times\mathcal{Z}}DX×Z从获取的训练数据,
输入空间X=(Rm)∗\mathcal{X}=(\mathbb{R}^m)^*X=(Rm)∗是mmm维的实值向量序列,目标空间Z=L∗\mathcal{Z}=L^*Z=L∗由字母集LLL组成的标签序列,训练数据集SSS中的每个样本由序列对(x,z)(\mathbf{x},\mathbf{z})(x,z)组成。目标序列z=(z1,z2,...,zU)\mathbf{z}=(z_1,z_2,...,z_U)z=(z1,z2,...,zU)长度小于等于输入序列x=(x1,x2,...,xT),i.e.U≤T\mathbf{x}=(x_1,x_2,...,x_T),i.e.U\le Tx=(x1,x2,...,xT),i.e.U≤T。输入序列和输出序列长度一般不同,因此没有先验知识可以对齐他们。
Temporal Classification的任务是使用训练数据SSS,学习一个分类器,能够将输入序列分成对应的目标序列h:X→Zh:\mathcal{X}\rightarrow\mathcal{Z}h:X→Z
从第一部分介绍,可以知道OCR任务本身就是一个Temporal Classification,翻译成了时间序列分类问题。其输入是卷积后得到特征图序列,输出的是字符序列。
之所以被称为Connectionist Temporal Classification,是这样理解的,原始输入的是一整张联结在一起未切分的字符图像,输出的是字符序列,因为没有对原始图像上的字符进行切分预处理,因此被称之为连接序列分类。
2.2 CTC问题描述

从网络输入到获取标签序列要分成两步:
第一步,可以将输入为长度为TTT的序列x=[x1,x2,...,xT]\mathbf{x}=[x_1,x_2,...,x_T]x=[x1,x2,...,xT](序列中每个xxx都是m维),输出为长度TTT的序列y=[y1,y2,...,yT]\mathbf{y}=[y_1,y_2,...,y_T]y=[y1,y2,...,yT](序列中每个yyy都是n维),参数为www的映射(即循环神经网络)定以为Nw:(Rm)T→(Rn)T\mathcal{N}_w:(\mathbb{R}^m)^T\rightarrow(\mathbb{R}^n)^TNw:(Rm)T→(Rn)T,y=Nw(x)\mathbf{y}=\mathcal{N}_w(\mathbf{x})y=Nw(x)。将ykty_k^tykt表示成第ttt个序列值为kkk的概率,L′TL'^TL′T表示长度为TTT的序列,其中每个元素取自字母集L′=L∪{blank}L'=L\cup\{blank\}L′=L∪{blank},序列L′TL'^TL′T也被称之为路径,表示成π\piπ。
根据以上定义给定输入x\mathbf{x}x,输出为路径π\piπ的概率可表示成:
p(π∣x)=∏t=1Tyπtt,∀π∈L′Tp(\pi|\mathbf{x})=\prod_{t=1}^{T}y_{\pi_t}^t,\forall\pi\in L'^T p(π∣x)=t=1∏Tyπtt,∀π∈L′T
其实,这里还有个条件,就是每一步输出之间是相互独立,上面的公式才能成立。
第二步,我们知道输入x\mathbf{x}x对应的标签序列为长度等于UUU的序列z=[z1,z2,...,zU],U≤T\mathbf{z}=[z_1,z_2,...,z_U],U\le Tz=[z1,z2,...,zU],U≤T,在第一步中循环神经网络给出的只是长度为TTT的中间序列y\mathbf{y}y,要和长度为UUU的标签序列z\mathbf{z}z对应,还需要定义个从中间序列到标签序列的映射B:L′T↦L<T\mathcal{B}:L'^T\mapsto L^{\lt T}B:L′T↦L<T,很明显,B\mathcal{B}B是一个多对一的映射。这个映射可以定义为移除中间序列中的重复相邻字符和空格占位符,如B(s−ta−tt−e)=B(s−t−aa−tt−e)=state\mathcal{B}(s-ta-tt-e)=\mathcal{B}(s-t-aa-tt-e)=stateB(s−ta−tt−e)=B(s−t−aa−tt−e)=state,定义了映射B\mathcal{B}B后,可以将输出标签序列z\mathbf{z}z的后验概率表示成:
p(z∣x)=∑π∈B−1(z)p(π∣x)p(\mathbf{z}|\mathbf{x})=\sum_{\pi\in\mathcal{B}^{-1}(\mathbf{z})}p(\pi|\mathbf{x}) p(z∣x)=π∈B−1(z)∑p(π∣x)
2.2关于对齐
为什么要使用上述的方法来进行网络的训练呢?那是因为输入x=[x1,x2,...,xm]\mathbf{x}=[x_1,x_2,...,x_m]x=[x1,x2,...,xm]和标签序列z=[z1,z2,...,zU]\mathbf{z}=[z_1,z_2,...,z_U]z=[z1,z2,...,zU]之间在序列长度,序列长度比例,对应元素之间找不到什么对应关系。

如上图是对齐后的数据,但在实际中是很难知道(x1,x2)↦c,(x3,x4,x5)↦a,(x6)↦t(x_1,x_2)\mapsto c,(x_3,x_4,x_5)\mapsto a,(x_6)\mapsto t(x1,x2)↦c,(x3,x4,x5)↦a,(x6)↦t,标注这样的数据也需要花费大量的时间,因此更希望模型能够拥有从未对齐数据中学习的能力,通过前面的介绍,使用CTC算法可以从未对齐的输入中求得标签序列。
2.3 前向后向算法

使用暴力方法计算
p(z∣x)=∑π∈B−1(z)p(π∣x)p(\mathbf{z}|\mathbf{x})=\sum_{\pi\in\mathcal{B}^{-1}(\mathbf{z})}p(\pi|\mathbf{x}) p(z∣x)=π∈B−1(z)∑p(π∣x)
因为要计算每一条路径,因此对于序列字典中有nnn个元素,长度为TTT的序列,要计算所有路径的概率,时间复杂度为O(nT)O(n^T)O(nT),这是指数级的时间复杂度,对于大部分长度的序列这个运算都过于耗时。论文作者为了解决这个问题,提出了前向后向递推算法,采用动态规划的方法将时间复杂度降到了O(nT)O(nT)O(nT),使算法更可行。
先借个例子来看一下。
假设标签序列为
z=state\mathbf{z} = state z=state
在序列前后和每个字符中间添加空格占位符−-−:
z′=−s−t−a−t−e−\mathbf{z}'=-s-t-a-t-e- z′=−s−t−a−t−e−
对z′\mathbf{z}'z′中任意的字符重复任意次,经过B\mathcal{B}B映射都能得到标签序列statestatestate,因此可以将z′\mathbf{z}'z′当成满足变换条件的基础序列。B\mathcal{B}B是多对一的映射,如下4个路径都能得到statestatestate
B(−−sttaa−tee−)=stateB(−−stta−t−−−e)=stateB(sst−aaa−tee−)=stateB(sst−aa−t−−−e)=state\mathcal{B}(--sttaa-tee-)=state\\ \mathcal{B}(--stta-t---e)=state\\ \mathcal{B}(sst-aaa-tee-)=state\\ \mathcal{B}(sst-aa-t---e)=state B(−−sttaa−tee−)=stateB(−−stta−t−−−e)=stateB(sst−aaa−tee−)=stateB(sst−aa−t−−−e)=state
将z′\mathbf{z}'z′写成列的形式,则上述四条路径可以写成如下图的形式:

从上图可以看到,四条路径在序列t=6t=6t=6时都经过字符aaa,记上面的四条路径为π1,π2,π3,π4\pi^1,\pi^2,\pi^3,\pi^4π1,π2,π3,π4
π1=b=b1:5+{a}6+b7:12π2=r=r1:5+{a}6+r7:12π3=b1:5+{a}6+r7:12π4=r1:5+{a}6+b7:12\pi^1=b=b_{1:5}+\{a\}_6+b_{7:12}\\ \pi^2=r=r_{1:5}+\{a\}_6+r_{7:12}\\ \pi^3=b_{1:5}+\{a\}_6+r_{7:12}\\ \pi^4=r_{1:5}+\{a\}_6+b_{7:12} π1=b=b1:5+{a}6+b7:12π2=r=r1:5+{a}6+r7:12π3=b1:5+{a}6+r7:12π4=r1:5+{a}6+b7:12
记ykty_k^tykt表示序列第ttt步元素为kkk的概率,则上面四条路径都包含ya6y_a^6ya6这一项,将计算上面四条路径的概率表示可以提取公因式写成:
foward=p(b1:5+r1:5∣x)=y−1∗y−2∗ys3∗yt4∗yt5+ys1∗ys2∗yt3∗y−4∗ya5backward=p(b7:12+r7:12∣x)=y−7∗yt8∗y−9∗y−10∗y−11∗ye12+ya7∗y−8∗yt9∗ye10∗ye11∗y−12foward = p(b_{1:5}+r_{1:5}|\mathbf{x}) = y_-^1*y_-^2*y_s^3*y_t^4*y_t^5 + y_s^1*y_s^2*y_t^3*y_-^4*y_a^5\\ backward = p(b_{7:12}+r_{7:12}|\mathbf{x}) = y_-^7*y_t^8*y_-^9*y_-^{10}*y_-^{11}*y_e^{12} + y_a^7*y_-^8*y_t^9*y_e^{10}*y_e^{11}*y_-^{12} foward=p(b1:5+r1:5∣x)=y−1∗y−2∗ys3∗yt4∗yt5+ys1∗ys2∗yt3∗y−4∗ya5backward=p(b7:12+r7:12∣x)=y−7∗yt8∗y−9∗y−10∗y−11∗ye12+ya7∗y−8∗yt9∗ye10∗ye11∗y−12
然后上面四条路径的概率和可以写成:
p(π1,π2,π3,π4∣x)=forward∗ya6∗backwardp(\pi^1,\pi^2,\pi^3,\pi^4|\mathbf{x}) = forward*y_a^6*backward p(π1,π2,π3,π4∣x)=forward∗ya6∗backward
上面的介绍中只取了四条经过变换B\mathcal{B}B后能得到statestatestate的路径,实际上的路径要远远多于此:

从上图中选出经过{a}6\{a\}_6{a}6的所有路径,概率∑B(π)=z,π6=ap(π∣x)\sum\limits_{\mathcal{B}(\pi)=\mathbf{z},\pi_6=a}p(\pi|x)B(π)=z,π6=a∑p(π∣x)(π6=a\pi_6=aπ6=a表示路径π\piπ的第6个字符为a),同样还是可以表示成如下形式:
∑B(π)=z,π6=ap(π∣x)=forward∗ya6∗backward\sum\limits_{\mathcal{B}(\pi)=\mathbf{z},\pi_6=a}p(\pi|x)=forward*y_a^6*backwardB(π)=z,π6=a∑p(π∣x)=forward∗ya6∗backward
进一步推广,定义αt(s)\alpha_t(s)αt(s)表示路径π\piπ中的第t个字符与加了占位符后标签序列z′\mathcal{z}'z′的第s个字相对应且路径π\piπ满足B(π1:t)=z1:s\mathcal{B}(\pi_{1:t})=\mathbf{z}_{1:s}B(π1:t)=z1:s时所有路径π1:t\pi_{1:t}π1:t的概率和,表示成:
αt(s)=∑B(π1:t)=留−z1:s′∏t′=1tyπt′t′\alpha_t(s)=\sum\limits_{\mathcal{B}(\pi_{1:t})\overset{留-}{=}\mathbf{z}'_{1:s}}\prod_{t'=1}^{t}y^{t'}_{\pi_{t'}} αt(s)=B(π1:t)=留−z1:s′∑t′=1∏tyπt′t′
可以看到这等同于前向变量forwardforwardforward,现在来看t=1t=1t=1时的α1(s)\alpha_1(s)α1(s),要经过B\mathcal{B}B映射后能得到保留占位符的标签序列,sss就只能等于1或者2,看上图中−s−t−a−t−e−-s-t-a-t-e-−s−t−a−t−e−的例子,t=1时刻只能取z′\mathcal{z}'z′的−-−或者sss,否则无法经过B\mathcal{B}B映射得到标签序列,因此
α1(1)=y−1α1(2)=yz2′1α1(s)=0,∀s>2\alpha_1(1)=y^1_{-}\\ \alpha_1(2)=y^1_{\mathbf{z}'_2}\\ \alpha_1(s)=0,\forall s\gt2 α1(1)=y−1α1(2)=yz2′1α1(s)=0,∀s>2
还看statestatestate的例子,当过z′6{\mathbf{z}'}_6z′6时,t=5t=5t=5对应的字符只能是t/−/at/-/at/−/a,可以推出来上面例子中
α6(6)=(α5(4)+α5(5)+α5(6))∗ya6\alpha_6(6)=(\alpha_5(4)+\alpha_5(5)+\alpha_5(6))*y_a^6 α6(6)=(α5(4)+α5(5)+α5(6))∗ya6
一般化推广可得:
αt(s)=(αt−1(s−2)+αt−1(s−1)+αt−1(s))∗yzs′t\alpha_t(s)=(\alpha_{t-1}(s-2)+\alpha_{t-1}(s-1)+\alpha_{t-1}(s))*y_{\mathbf{z}'_s}^{t} αt(s)=(αt−1(s−2)+αt−1(s−1)+αt−1(s))∗yzs′t
还需考虑一个特殊情况,看下面例子z=zoo,z′=−z−o−o−\mathbf{z}=zoo,\mathbf{z}'=-z-o-o-z=zoo,z′=−z−o−o−,t=2,s=6或3:

很明显因为B\mathcal{B}B映射会去除重复的字母,因此上面两种情况在t−1t-1t−1时刻不能取s−2s-2s−2
综上,可得最终t≥2t\ge2t≥2时前向递推公式为(也就是原论文上的递推公式):
αt(s)={(αt−1(s−1)+αt−1(s))∗yzs′tifzs′=−orzs′=zs−2′(αt−1(s−2)+αt−1(s−1)+αt−1(s))∗yzs′totherwise\alpha_t(s)=\left\{\begin{matrix} (\alpha_{t-1}(s-1)+\alpha_{t-1}(s))*y_{\mathbf{z}'_s}^{t}\,if\,z'_s=-\,or\,z'_s=z'_{s-2} \\ (\alpha_{t-1}(s-2)+\alpha_{t-1}(s-1)+\alpha_{t-1}(s))*y_{\mathbf{z}'_s}^{t}\,otherwise \end{matrix}\right. αt(s)={(αt−1(s−1)+αt−1(s))∗yzs′tifzs′=−orzs′=zs−2′(αt−1(s−2)+αt−1(s−1)+αt−1(s))∗yzs′totherwise
将公式中相同的项合并一下就可以得到论文上的公式了。
同样的方法可以定义backwardbackwardbackward:
βt(s)=∑B(πt:T)=留−zs:∣z′∣′∏t′=tTyπt′t′\beta_t(s)=\sum\limits_{\mathcal{B}(\pi_{t:T})\overset{留-}{=}\mathbf{z}'_{s:|z'|}}\prod_{t'=t}^{T}y^{t'}_{\pi_{t'}} βt(s)=B(πt:T)=留−zs:∣z′∣′∑t′=t∏Tyπt′t′
t≥2t\ge2t≥2时βt(s)\beta_t(s)βt(s)的递推公式:
βt(s)={(βt+1(s)+βt+1(s+1))∗yzs′tifzs′=−orzs′=zs+2′(βt+1(s)+βt+1(s+1)+βt+1(s+2))∗yzs′totherwise\beta_t(s)=\left\{\begin{matrix} (\beta_{t+1}(s)+\beta_{t+1}(s+1))*y_{\mathbf{z}'_s}^{t}\,if\,z'_s=-\,or\,z'_s=z'_{s+2} \\ (\beta_{t+1}(s)+\beta_{t+1}(s+1)+\beta_{t+1}(s+2))*y_{\mathbf{z}'_s}^{t}\,otherwise \end{matrix}\right. βt(s)={(βt+1(s)+βt+1(s+1))∗yzs′tifzs′=−orzs′=zs+2′(βt+1(s)+βt+1(s+1)+βt+1(s+2))∗yzs′totherwise
求得αt(s)\alpha_t(s)αt(s)和βt(s)\beta_t(s)βt(s)后,标签序列z\mathbf{z}z的后验概率可以写成,
p(z∣x)=∑zs′∈πtαt(s)βt(s)yzs′tp(\mathbf{z}|\mathbf{x})=\sum_{z'_s\in\pi_t}\frac{\alpha_t(s)\beta_t(s)}{y_{z'_s}^t} p(z∣x)=zs′∈πt∑yzs′tαt(s)βt(s)
求得p(z∣x)p(\mathbf{z}|\mathbf{x})p(z∣x)后,可以知道使用CTCCTCCTC时的目标就是最大化p(z∣x)p(\mathbf{z}|\mathbf{x})p(z∣x),可以定义损失函数为−log(p(z∣x))-log(p(\mathbf{z}|\mathbf{x}))−log(p(z∣x)),可以推导损失的计算和损失函数梯度都能使用递推的方式来计算,减少运算量,加快运算速度。
2.4 推理时
训练完成后,在网络推理时希望取概率最大的输出序列:
z∗=argmaxzp(z∣x)\mathbf{z}^* = \underset{\mathbf{z}}{argmax} \,p(\mathbf{z}|\mathbf{x}) z∗=zargmaxp(z∣x)
对所有路径的概率求和,然后取概率最大的路径作为预测的结果,应该是最合理的方式,但当序列比较长时面临计算量过大,影响推理速度的情况。
一种做法是对于第ttt步,取概率最大的字符,然后将所有的字符组合起来经过去重当作最终的输出,但这种做法只考虑了一条路径,有可能有多条路径对应标签,各条路径的概率加和后有可能更大。
一种替代的折衷方法是改进版的Beam Search。
常规的Beam Search算法,对于每个时间步取概率最大的几个(Beam Size)可能结果,如下为字母集为−,a,b-,a,b−,a,b,Beam Size=3的Beam Search的过程:
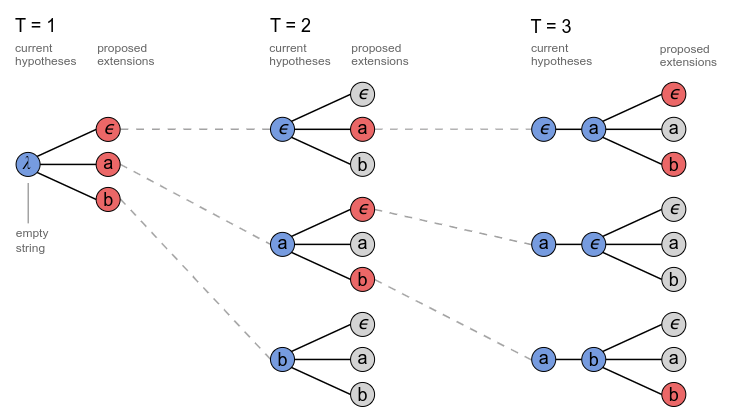
上图中Beam Search到当前步最大的几个(Beam Size)可能字符都只有一条前缀序列,实际上可以有多条前缀序列和当前的字符组合后都得到相同的输出,如下图对于路径长度T=2T=2T=2时λa\lambda aλa,a−a-a−,aaaaaa最后都能对应的aaa
且观察T=3T=3T=3时,前缀序列aaaaaa对应的输出有可能是aaa或者aaaaaa,因此对应的概率应该分别进行计算。
3.pytorch中的CTCLOSS
计算未切分的连续时间序列和目标序列之间的损失。
torch.nn.CTCLoss(blank=0, reduction='mean', zero_infinity=False)class CTCLoss:...def forward(self, log_probs: Tensor, targets: Tensor, input_lengths: Tensor, target_lengths: Tensor) -> Tensor:...-
log_probs:Tensor of size (T,N,C)/(T,C),T是输入长度,N是
Batch Size,C是序列字典的大小(包括空格) -
targets:Tensor of size(N,S)
N是batch size,S是最大目标序列长度,目标序列中的每个元素是类别的序号。 -
input_lengths,每个输入序列的长度,为元组tuple或shape为(N,)的张量,N是batch size,input_lengths的值≤T\le T≤T -
target_lengths,每个目标序列的长度,为元组tuple或shape为(N,)的张量,N是batch size,如果targets的shape是(N,S),这里其实是把每个targettargettarget添加padding后变成了S,假设第n个序列目标长度为sns_nsn,target_lengths中第n个元素值就为sns_nsn。
import torchT = 2
C = 3
N = 1
S = 2
S_min = 1input = torch.randn(T,N,C).log_softmax(2).detach().requires_grad_()
print(input)
target = torch.tensor([0,1], dtype=torch.long).reshape(shape=(N, S))
print(target)
input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.tensor([2], dtype=torch.long).reshape(shape=(N,))
ctc_loss = torch.nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
print(loss)# tensor([[[-0.4002, -1.5314, -2.1752]], [[-0.8444, -2.2039, -0.7770]]], requires_grad=True)
# tensor([[0, 1]])
# tensor(1.3021, grad_fn=<MeanBackward0>)
上面示例的计算过程:

从上图可以看到目标是010101即at路径有且仅有此一条,损失值计算为:
loss=−12[−0.4002+(−2.2039)]=1.3021loss = -\frac{1}{2}[-0.4002+(-2.2039)]=1.3021 loss=−21[−0.4002+(−2.2039)]=1.3021
欢迎访问个人网络日志🌹🌹知行空间🌹🌹
参考资料
- 1.https://distill.pub/2017/ctc/
- 2.https://zhuanlan.zhihu.com/p/161186907
- 3.https://zhuanlan.zhihu.com/p/519960905
- 4.https://zhuanlan.zhihu.com/p/58526617
相关文章:

4.OCR文本识别Connectionist Temporal Classification(CTC)算法
文章目录1.基础介绍2.Connectionist Temporal Classification(CTC)算法2.1 什么是Temporal Classification2.2 CTC问题描述2.2关于对齐2.3 前向后向算法2.4 推理时3.pytorch中的CTCLOSS参考资料欢迎访问个人网络日志🌹🌹知行空间🌹dz…...

误删了Ubuntu/Linux的一些默认用户目录怎么办?
用户目录:指位于 $HOME 下的一系列常用目录,例如 Documents,Downloads,Music,还有 Desktop等。本文不是讲如何恢复原有目录及其重要文件,适用于仅恢复目录功能一:仅恢复个别目录如误删了Desktop…...
ArXiv简介以及论文提交
arXiv网站简介 arXiv是一个收集物理学、数学、计算机科学、生物学与数理经济学的论文预印本的网站。其中arXiv发音同“archive”,因为“X”代表希腊字母 ,国际音标为[kai]。它于1991年8月14日成立,现由美国康奈尔大学维护。 ——维基百科 对…...

pytorch学习
目录如下: pytorch常用操作 pytorch 常用操作 pytorch 的 detach()函数 1. 什么是detach()函数 我们在将输出特征矩阵进行存储的时候,经常需要将torch.Tensor类型的数据转换成别的如numpy类型的数据,但是Tensor类型的数据是会自动计算梯度…...
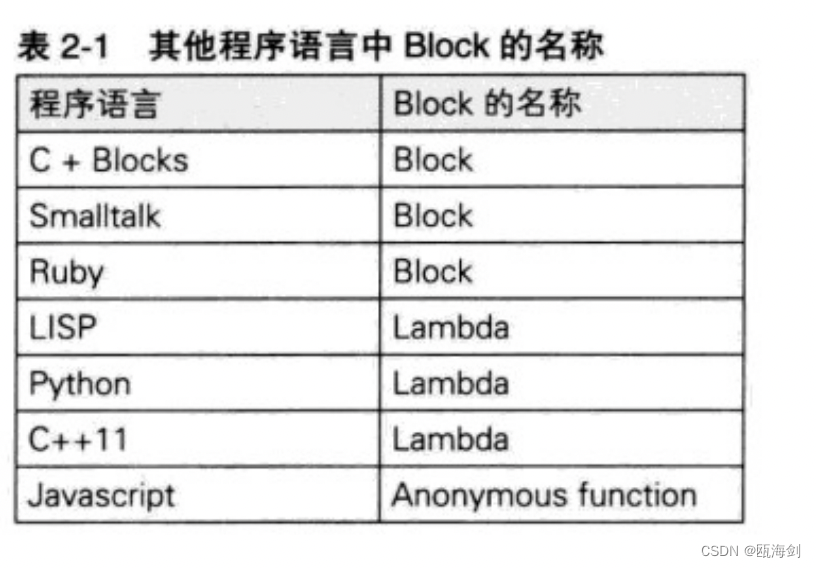
【OC】块初识
Block简介 Blocks是C语言的扩充功能。可以用一句话来表示Blocks的扩充功能:带有自动变量的匿名函数。 匿名函数 所谓匿名函数就是不带有名称的函数。C语言的标准不允许存在这样的函数。例: int func(int count);它声明了名称为func的函数。下面的源代…...
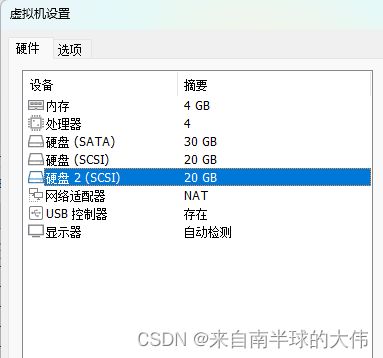
3-2 创建一个至少有两个PV组成的大小为20G的名为testvg的VG
文章目录1. 在vmware添加多块20G的硬盘,并创建分区2. 创建一个至少有两个PV组成的大小为20G的名为testvg的VG,要求PE大小为16M,而后在卷组中创建大小为5G的逻辑卷testlv;挂载至/users目录3. 新建用户archlinux,要求其家目录为/users/archlinu…...

【密码学】 一篇文章讲透数字证书
【密码学】 一篇文章讲透数字证书 数字证书介绍 数字证书是一种用于认证网络通信中参与者身份和加密通信的证书,人们可以在网上用它来识别对方的身份。 我们在上一篇博客中介绍了数字签名的作用和原理,数字签名可以防止消息被否认。有了公钥算法和数字签…...
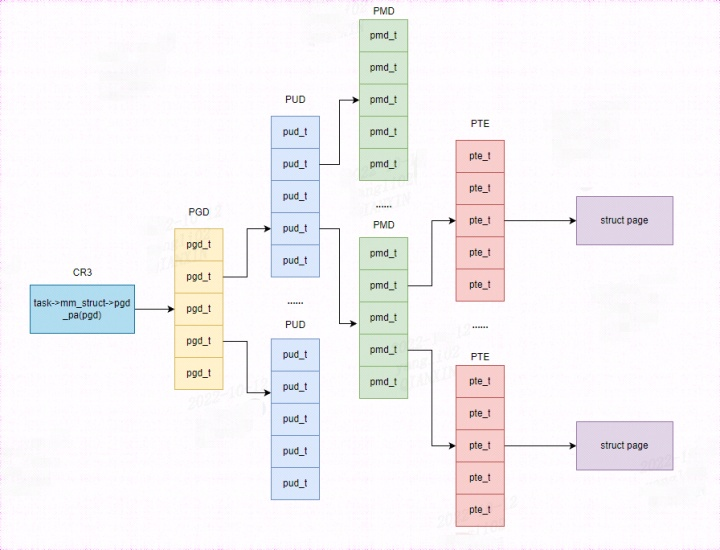
Linux 操作系统原理 — 内存管理 — 虚拟地址空间(x86 64bit 系统)
目录 文章目录目录虚拟地址格式与内核页表(四级页表)虚拟地址格式与内核页表(四级页表) 在 x86 64bit 系统中,可以描述的最长地址空间为 2^64(16EB),远远超过了目前主流内存卡的规格…...
指针的深入理解)
C语言深入知识——(2)指针的深入理解
1、字符指针 (1)字符指针的普通用法 char a A; char* pa &a;但是一般来说字符指针很少这么用……更多是拿来存储一个字符串 (2)字符串的两种存储以及区别 现在有了两种存储数组的方法 ①一个是使用char类型数组存储②另外…...
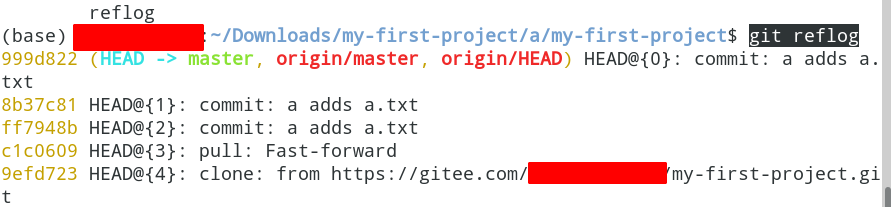
Git使用笔记
分支branch切换到另一个分支git checkout 你要切换到的分支的名字git checkout master将本地的这个分支branch1和gitee上的branch1进行合并(本地的branch1有的,gitee上branch1没有的增加上去)git merge branch1git merge 分支的名字查看本地是…...

数据库管理-第五十八期 倒腾PDB(20230226)
数据库管理 2023-02-26第五十八期 倒腾PDB1 克隆本地PDB2 没开归档总结第五十八期 倒腾PDB 其实本周过的不大好,连着两天熬夜,一次是割接一次是处理ADG备库的异常,其实本周有些内容是以前处理过的问题,到了周末还肚子痛。哎… 1…...

我看谁还敢说不懂git
文章目录一、Git介绍1.1、Git的作用1.2、Git的理念1.3、Git的特点1.4、Git对比SVN二、Git的概念2.1、Git基础概念三、Git的基本操作3.1、使用Git管理一个代码仓库的流程3.2、Git常用命令介绍四、Git状态的变化五、Git安装和配置5.1、Git的安装5.2、Git的配置六、Git的高级操作6…...

Scratch少儿编程案例-算法练习-实现加减乘除练习题
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...
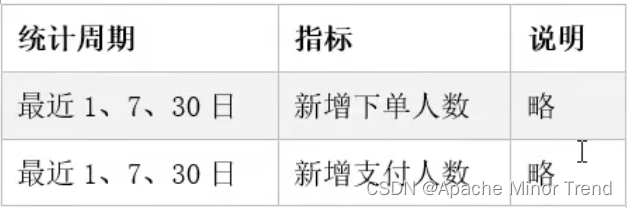
【离线数仓-9-数据仓库开发DWS层设计要点-1d/nd/td表设计】
离线数仓-9-数据仓库开发DWS层设计要点-1d/nd/td表设计离线数仓-9-数据仓库开发DWS层设计要点-1d/nd/td表设计一、DWS层设计要点二、DWS层设计分析 - 1d/nd1.DWS层设计一:不考虑用户维度2.DWS层设计二:考虑用户维度2.DWS层设计三 :考虑用户商…...

python网络数据获取
文章目录1网络爬虫2网络爬虫的类型2.1通用网络爬虫2.1.12.1.22.2聚焦网络爬虫2.2.1 基于内容评价的爬行策略2.2.2 基于链接结构的爬行策略2.2.3基于增强学习的爬行策略2.2.4基于语境图的爬行策略2.3增量式网络爬虫深层网页爬虫3网络爬虫基本架构3.1URL管理模块3.2网页下载模块3…...
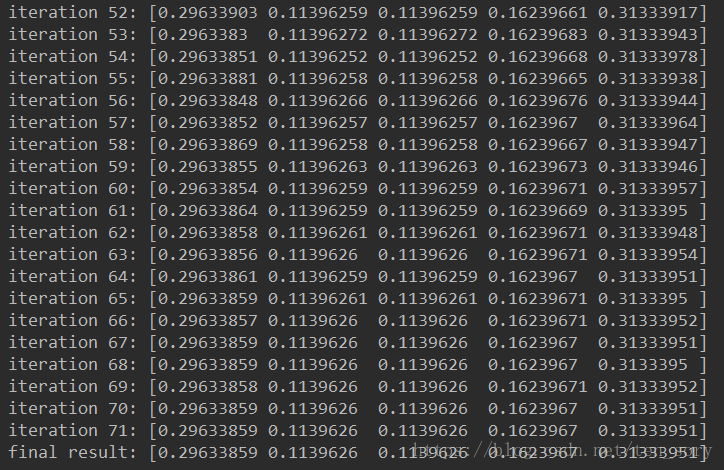
[Datawhale][CS224W]图机器学习(六)
目录一、简介二、概述三、算法四、PageRank的缺点五、Python实现迭代法参考文献一、简介 PageRank,又称网页排名、谷歌左侧排名、PR,是Google公司所使用的对其搜索引擎搜索结果中的网页进行排名的一种算法。 佩奇排名本质上是一种以网页之间的超链接个…...

aws ecr 使用golang实现的简单镜像转换工具
https://pkg.go.dev/github.com/docker/docker/client#section-readme 通过golang实现一个简单的镜像下载工具 总体步骤 启动一台海外区域的ec2实例安装docker和awscli配置凭证访问国内ecr仓库编写web服务实现镜像转换和自动推送 安装docker和awscli sudo yum remove awsc…...

【20230225】【剑指1】分治算法(中等)
1.重建二叉树class Solution { public:TreeNode* traversal(vector<int>& preorder,vector<int>& inorder){if(preorder.size()0) return NULL;int rootValuepreorder.front();TreeNode* rootnew TreeNode(rootValue);//int rootValuepreorder[0];if(preo…...
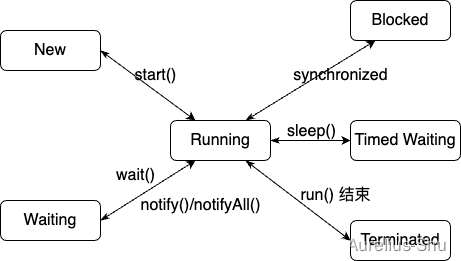
「JVM 高效并发」Java 线程
进程是资源分配(内存地址、文件 I/O 等)的基本单位,线程是执行调度(处理器资源调度)的基本单位; Loom 项目若成功为 Java 引入纤程(Fiber),则线程的执行调度单位可能变为…...

ADAS-可见光相机之Cmos Image Sensor
引言 “ 可见光相机在日常生活、工业生产、智能制造等应用有着重要的作用。在ADAS中更是扮演着重要的角色,如tesla model系列全车身10多个相机,不断感知周围世界。本文着重讲解下可见光相机中的CIS(CMOS Image Sensor)。” 定义 光是一种电磁波&…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
