16- TensorFlow实现线性回归和逻辑回归 (TensorFlow系列) (深度学习)
知识要点
线性回归要点:
- 生成线性数据: x = np.linspace(0, 10, 20) + np.random.rand(20)
- 画点图: plt.scatter(x, y)
- TensorFlow定义变量: w = tf.Variable(np.random.randn() * 0.02)
- tensor 转换为 numpy数组: b.numpy()
- 定义优化器: optimizer = tf.optimizers.SGD()
- 定义损失: tf.reduce_mean(tf.square(y_pred - y_true)) # 求均值
- 自动微分: tf.GradientTape()
- 计算梯度: gradients = g.gradient(loss, [w, b])
- 更新w, b: optimizer.apply_gradients(zip(gradients, [w, b]))
逻辑回归要点:
- 查看安装文件: pip list
- 聚类数据生成器: make_blobs
- 生成聚类数据: data, target = make_blobs(centers = 3)
- 转换为tensor 数据: x = tf.constant(data, dtype = tf.float32)
- 定义tensor变量: B = tf.Variable(0., dtype = tf.float32)
- 矩阵运算: tf.matmul(x, W)
- 返回值长度为batch_size的一维Tensor: tf.sigmoid(linear)
- 调整形状: y_pred = tf.reshape(y_pred, shape = [100])
- tf.clip_by_value(A, min, max):输入一个张量A,把A中的每一个元素的值都压缩在min和max之间。
- 求均值: tf.reduce_mean()
- 定义优化器: optimizer = tf.optimizers.SGD()
- 计算梯度: gradients = g.gradient(loss, [W, B]) # with tf.GradientTape() as g
- 迭代更新W, B: optimizer.apply_gradients(zip(gradients, [W, B]))
- 准确率计算: (y_ == y_true).mean()
1 使用tensorflow实现 线性回归
实现一个算法主要从以下三步入手:
-
找到这个算法的预测函数, 比如线性回归的预测函数形式为:y = wx + b,
-
找到这个算法的损失函数 , 比如线性回归算法的损失函数为最小二乘法
-
找到让损失函数求得最小值的时候的系数, 这时一般使用梯度下降法.
使用TensorFlow实现算法的基本套路:
-
使用TensorFlow中的变量将算法的预测函数, 损失函数定义出来.
-
使用梯度下降法优化器求损失函数最小时的系数
-
分批将样本数据投喂给优化器,找到最佳系数
1.1 导包
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression1.2 生成线性数据
# 生成线性数据
x = np.linspace(0, 10, 20) + np.random.rand(20)
y = np.linspace(0, 10, 20) + np.random.rand(20)
plt.scatter(x, y)
1.3 初始化斜率变量
# 把w,b 定义为变量
w = tf.Variable(np.random.randn() * 0.02)
b = tf.Variable(0.)
print(w.numpy(), b.numpy()) # -0.031422824 0.01.4 定义线性模型和损失函数
# 定义线性模型
def linear_regression(x):return w * x +b# 定义损失函数
def mean_square_loss(y_pred, y_true):return tf.reduce_mean(tf.square(y_pred - y_true))1.5 定义优化过程
# 定义优化器
optimizer = tf.optimizers.SGD()
# 定义优化过程
def run_optimization():# 把需要求导的计算过程放入gradient pape中执行,会自动实现求导with tf.GradientTape() as g:pred = linear_regression(x)loss = mean_square_loss(pred, y)# 计算梯度gradients = g.gradient(loss, [w, b])# 更新w, boptimizer.apply_gradients(zip(gradients, [w, b]))1.6 执行迭代训练过程
# 训练
for step in range(5000):run_optimization() # 持续迭代w, b# z展示结果if step % 100 == 0:pred = linear_regression(x)loss = mean_square_loss(pred, y)print(f'step:{step}, loss:{loss}, w:{w.numpy()}, b: {b.numpy()}')
1.7 线性拟合
linear = LinearRegression() # 线性回归
linear.fit(x.reshape(-1, 1), y)plt.scatter(x, y)
x_test = np.linspace(0, 10, 20).reshape(-1, 1)
plt.plot(x_test, linear.coef_ * x_test + linear.intercept_, c='r') # 画线
plt.plot(x_test, w.numpy() * x_test + b.numpy(), c='g', lw=10, alpha=0.5) # 画线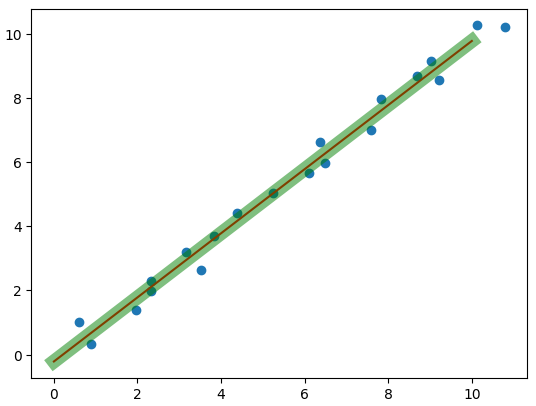
2. 使用TensorFlow实现 逻辑回归
实现逻辑回归的套路和实现线性回归差不多, 只不过逻辑回归的目标函数和损失函数不一样而已.
使用tensorflow实现逻辑斯蒂回归
- 找到预测函数 :
- 找到损失函数 : -(y_true * log(y_pred) + (1 - y_true)log(1 - y_pred))
- 梯度下降法求损失最小的时候的系数
2.1 导包
import tensorflow as tf
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt- 聚类数据生成器: make_blobs
2.2 描聚类数据点
data, target = make_blobs(centers = 3)
plt.scatter(data[:, 0] , data[:, 1], c = target)
x = data.copy()
y = target.copy()
print(x.shape, y.shape) # (100, 2) (100,)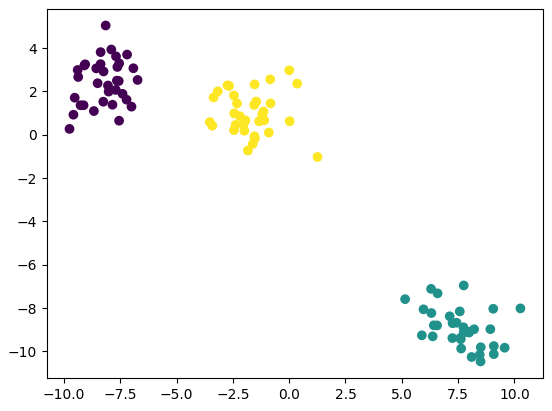
2.3 数据转换为张量 (tensor)
x = tf.constant(data, dtype = tf.float32)
y = tf.constant(target, dtype = tf.float32)2.4 定义预测函数
# 定义预测变量
W = tf.Variable(np.random.randn(2, 1) * 0.2, dtype = tf.float32)
B = tf.Variable(0., dtype = tf.float32)2.5 定义目标函数
def sigmoid(x):linear = tf.matmul(x, W) + Breturn tf.nn.sigmoid(linear)2.6 定义损失
# 定义损失
def cross_entropy_loss(y_true, y_pred):# y_pred 是概率,存在可能性是0, 需要进行截断y_pred = tf.reshape(y_pred, shape = [100])y_pred = tf.clip_by_value(y_pred, 1e-9, 1)return tf.reduce_mean(-(tf.multiply(y_true, tf.math.log(y_pred)) + tf.multiply((1 - y_pred),tf.math.log(1 - y_pred))))2.7 定义优化器
# 定义优化器
optimizer = tf.optimizers.SGD()def run_optimization():with tf.GradientTape() as g:# 计算预测值pred = sigmoid(x) # 结果为概率loss = cross_entropy_loss(y, pred)#计算梯度gradients = g.gradient(loss, [W, B])# 更新W, Boptimizer.apply_gradients(zip(gradients, [W, B]))2.8 定义准确率
# 计算准确率
def accuracy(y_true, y_pred):# 需要把概率转换为类别# 概率大于0.5 可以判断为正例y_pred = tf.reshape(y_pred, shape = [100])y_ = y_pred.numpy() > 0.5y_true = y_true.numpy()return (y_ == y_true).mean()2.9 开始训练
# 定义训练过程
for i in range(5000):run_optimization()if i % 100 == 0:pred = sigmoid(x)acc = accuracy(y, pred)loss = cross_entropy_loss(y, pred)print(f'训练次数:{i}, 准确率: {acc}, 损失: {loss}')
相关文章:

16- TensorFlow实现线性回归和逻辑回归 (TensorFlow系列) (深度学习)
知识要点 线性回归要点: 生成线性数据: x np.linspace(0, 10, 20) np.random.rand(20)画点图: plt.scatter(x, y)TensorFlow定义变量: w tf.Variable(np.random.randn() * 0.02)tensor 转换为 numpy数组: b.numpy()定义优化器: optimizer tf.optimizers.SGD()定义损失: …...

无自动化测试系统设计方法论
灵活 敏捷 迭代。 自动化测试 辩思 测试必不可少 想想看没有充分测试的代码, 哪一次是一次过的? 哪一次不需要经历下测试的鞭挞? 不要以为软件代码容易改, 就对于质量不切实际的自信—那是自大! 不适用自动化测试的case 遗留系统。太多的依赖方, 不想用过多的mock > …...
架构初探-学习笔记
1 什么是架构 有关软件整体结构与组件的抽象描述,用于指导软件系统各个方面的设计。 1.1 单机架构 所有功能都实现在一个进程里,并部署在一台机器上。 1.2 单体架构 分布式部署单机架构 1.3 垂直应用架构 按应用垂直切分的单体架构 1.4 SOA架构 将…...

在成都想转行IT,选择什么专业比较好?
很多创新型的互联网服务公司的核心其实都是软件,创新的基础、运行的支撑都是软件。例如,软件应用到了出租车行业,就形成了巅覆行业的滴滴;软件应用到了金融领域,就形成互联网金融;软件运用到餐饮行业,就形成美团;软件运…...
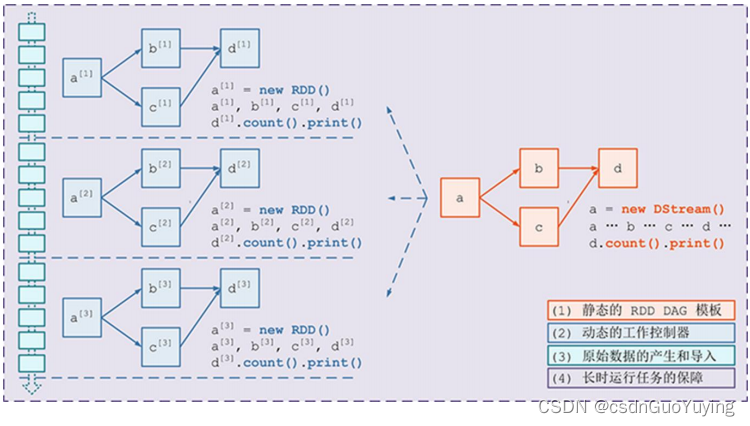
【Spark分布式内存计算框架——Spark Streaming】4.入门案例(下)Streaming 工作原理
2.3 Streaming 工作原理 SparkStreaming处理流式数据时,按照时间间隔划分数据为微批次(Micro-Batch),每批次数据当做RDD,再进行处理分析。 以上述词频统计WordCount程序为例,讲解Streaming工作原理。 创…...
2、算法先导---思维能力与工具
题目 碎纸片的拼接复原(2013B) 内容 破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。传统上,拼接复原工作需由人工完成,准确率较高,但效率很低。特别是当碎片数量巨大,人工拼接很难在短时…...

WordPress 函数:add_theme_support() 开启主题自定义功能(全面)
add_theme_support() 用于在我们的当前使用的主题添加一些特殊的功能,函数一般写在主题的functions.php文件中,当然也可以再插件中使用钩子来调用该函数,如果是挂在钩子上,那他必须挂在after_setup_theme钩子上,因为 i…...

Winform控件开发(16)——Timer(史上最全)
前言: Timer控件的作用是按用户定义的时间间隔引发事件的计时器,说的直白点就是,他就像一个定时炸弹一样到了一定时间就爆炸一次,区别在于定时炸弹炸完了就不会再次爆炸了,但是Timer这个计时器到了下一个固定时间还会触发一次,上面那张图片就是一个典型的计时器,该定时器…...

游戏高度可配置化:通用数据引擎(data-e)及其在模块化游戏开发中的应用构想图解
游戏高度可配置化:通数据引擎在模块化游戏开发中的应用构想图解 ygluu 码客 卢益贵 目录 一、前言 二、模块化与插件 1、常规模块化 2、插件式模块化(插件开发) 三、通用数据引擎理论与构成 1、名字系统(数据类型…...
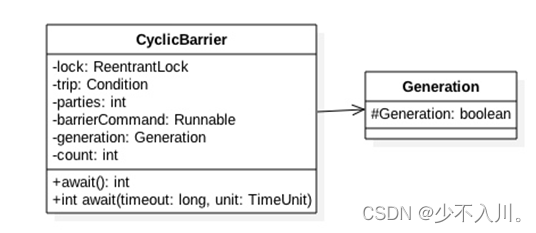
CountDownLatch与CyclicBarrier原理剖析
1.CountDownLatch 1.1 什么是CountDownLatch CountDownLatch是一个同步工具类,用来协调多个线程之间的同步,或者说起到线程之间的通信(而不是用作互斥的作用)。 CountDownLatch能够使一个线程在等待另外一些线程完成各自工作之…...
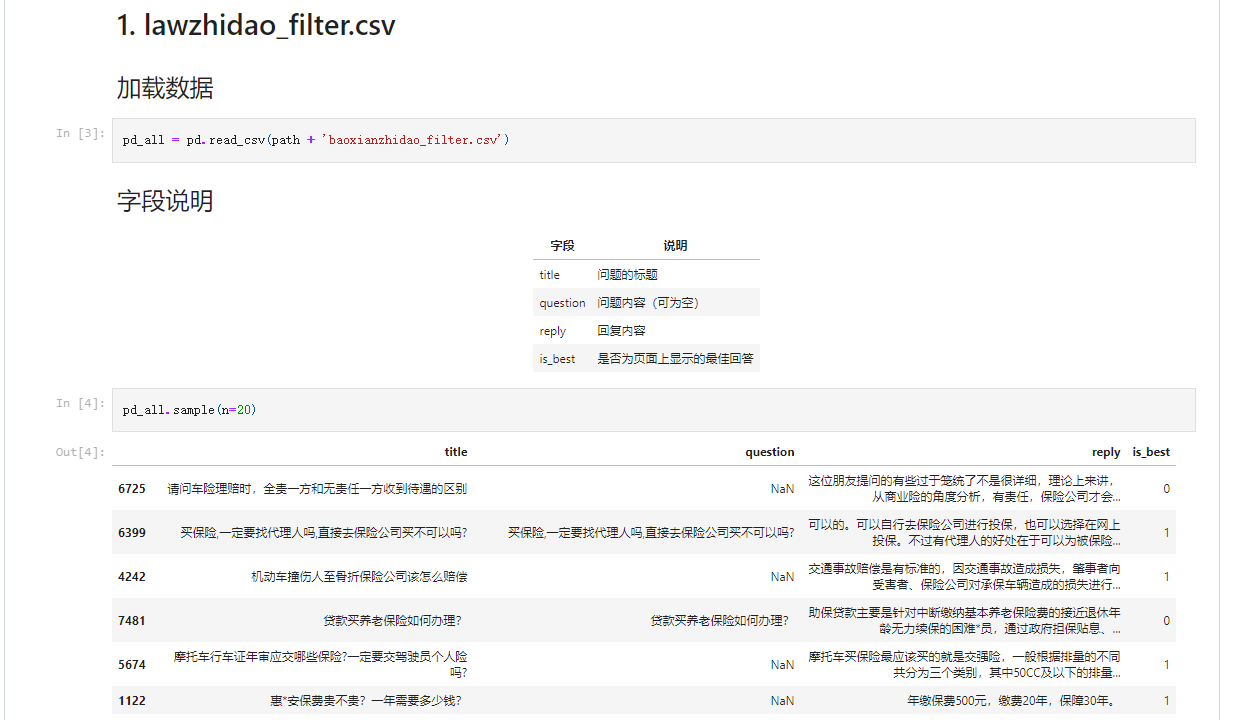
NLP中的对话机器人——预训练基准模型
引言 本文是七月在线《NLP中的对话机器人》的视频笔记,主要介绍FAQ问答型聊天机器人的实现。 场景二 上篇文章中我们解决了给定一个问题和一些回答,从中找到最佳回答的任务。 在场景二中,我们来实现: 给定新问题,从…...

C语言学习及复习笔记-【14】C文件读写
14 C文件读写 14.1打开文件 您可以使用 fopen( ) 函数来创建一个新的文件或者打开一个已有的文件,这个调用会初始化类型 FILE 的一个对象,类型 FILE包含了所有用来控制流的必要的信息。下面是这个函数调用的原型: FILE *fopen( const char…...

模拟退火算法优化灰色
clc; clear; close all; warning off; %% tic T01000; % 初始温度 Tend1e-3; % 终止温度 L200; % 各温度下的迭代次数(链长) q0.9; %降温速率 X[16.4700 96.1000 16.4700 94.4400 20.0900 92.5400 22.3900 93.3700 25.…...
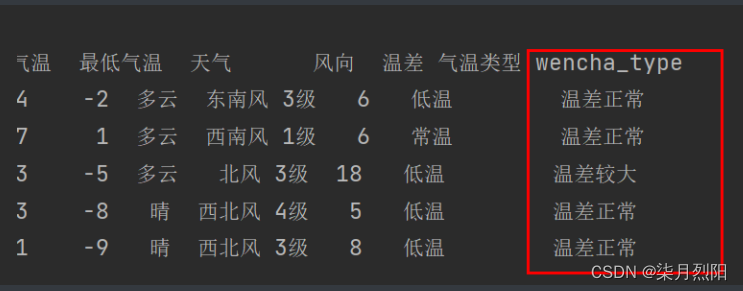
Pandas怎么添加数据列删除列
Pandas怎么添加数据列 1、直接赋值 # 1、直接赋值df.loc[:, "最高气温"] df["最高气温"].str.replace("℃", "").astype("int32")df.loc[:, "最低气温"] df["最低气温"].str.replace("℃"…...

C++类和对象:构造函数和析构函数
目录 一. 类的六个默认成员函数 二. 构造函数 2.1 什么是构造函数 2.2 编译器自动生成的默认构造函数 2.3 构造函数的特性总结 三. 析构函数 3.1 什么是析构函数 3.2 编译器自动生成的析构函数 3.3 析构函数的特性总结 一. 类的六个默认成员函数 对于任意一个C类&…...
【Stata】从入门到精通.零基础小白必学的教程,一学就fei
视频教程移步:https://www.bilibili.com/video/BV1hK4y1d714/?p4&spm_id_frompageDriver&vd_sourcecc8074e9c81a225f214226065db53d32P3 第二讲 Stata处理数据全流程(上) P3 - 01:37内置数据 file example datasets使用…...

【RuoYi优化】调整JVM启动内存
📔 笔记介绍 大家好,千寻简笔记是一套全部开源的企业开发问题记录,毫无保留给个人及企业免费使用,我是作者星辰,笔记内容整理并发布,内容有误请指出,笔记源码已开源,前往Gitee搜索《chihiro-notes》,感谢您的阅读和关注。 作者各大平台直链: GitHub | Gitee | CSD…...

[架构模型]MVC模型详细介绍,并应用到unity中
简介: MVC模式是一种软件架构模式,它将应用程序分为三个主要部分:模型(Model)、视图(View)和控制器(Controller)。MVC模式的目标是实现应用程序的松耦合,以便…...

?? JavaScript 双问号(空值合并运算符)
?? JavaScript 双问号(空值合并运算符) 一、简述 在网上浏览 JavaScript 代码时或者学习其他代码时,可能会发现有的表达式用了两个问号(??)如下所示: let username; console.log(username ?? "Guest"…...
作业2.25----通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作
1.通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作 例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输入led2off,开饭led2灯熄灭 5.例如在串口输入led…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
