【学习笔记】CF1895G Two Characters, Two Colors
感谢grass8sheep提供的思路。
首先,我们可以用 D P DP DP解决这个问题。
设 f i , j f_{i,j} fi,j表示前 i i i个数中有 j j j个为 1 1 1的位置为红色的最大价值。则转移如下:
- f i , j ← f i − 1 , j + b i f_{i,j}\gets f_{i-1,j}+b_i fi,j←fi−1,j+bi
- 若 s i = 1 s_i=1 si=1,有转移 f i , j ← f i − 1 , j − 1 + r i f_{i,j}\gets f_{i-1,j-1}+r_i fi,j←fi−1,j−1+ri
- 若 s i = 0 s_i=0 si=0,有转移 f i , j ← f i − 1 , j − j + r i f_{i,j}\gets f_{i-1,j}-j+r_i fi,j←fi−1,j−j+ri
初始 f 0 , j = 0 f_{0,j}=0 f0,j=0。
考虑差分序列,记作 { d i } \{d_i\} {di}。则 s i = 1 s_i=1 si=1的转移等价于,对于一段连续的满足 < r i − b i <r_i-b_i <ri−bi的区间,将 d i d_i di向后依次挪动一位,然后在开头插入 r i − b i r_i-b_i ri−bi(记为操作一)。 s i = 2 s_i=2 si=2则等价于,对于 [ 1 , r i − b i ] [1,r_i-b_i] [1,ri−bi]这段前缀的 d i d_i di减去 1 1 1(记为操作二)。注意如果 r i − b i < 0 r_i-b_i<0 ri−bi<0那么一定是贪心的选择 b i b_i bi。
但是打表可以发现,答案不是凸的,也就是说 d i d_i di不具有单调性。事实上有一个结论:每次结束后,将 d i d_i di按从大到小排序,这并不会影响答案。因此用平衡树维护即可,操作一对应区间平移;操作二对应前缀减 1 1 1,然后将差值为一的两个连续段交换。
复杂度 O ( n log n ) O(n\log n) O(nlogn)。
关于结论的证明:设 d p j dp_j dpj表示考虑完前 i i i个数后选了 j j j个 1 1 1的最大价值, d p j = a dp_{j}=a dpj=a, d p j + 1 = a + b dp_{j+1}=a+b dpj+1=a+b, d p j + 2 = a + 2 b + 1 dp_{j+2}=a+2b+1 dpj+2=a+2b+1。设之后的方案中选了 x x x个 0 0 0,那么我们要让 d p i − i x dp_i-ix dpi−ix最大。发现交换了 d j + 1 d_{j+1} dj+1和 d j + 2 d_{j+2} dj+2后 j + 1 j+1 j+1仍然不可能成为答案。(考虑是一条直线来截每个点使得截矩最大,因为斜率是整数,而相邻两点间斜率之差又不超过 1 1 1,因此不可能截到中间那个点)
因为每次操作是前缀减 1 1 1,所以交换的两个段之差不会超过 1 1 1,因此结论是正确的。
remark \text{remark} remark 注意到 D P DP DP只要不漏就好了,因此在不影响正确性的情况下我们可以修正 D P DP DP值。
类似的 D P DP DP思路:[USACO21DEC] Paired Up P(做法不一样,但是都有对 D P DP DP最优性的一些思考)
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define inf 0x3f3f3f3f3f3f3f3f
#define fi first
#define se second
using namespace std;
const int N=4e5+5;
int T,n,tot,rt;
ll r[N],b[N];
string str;
mt19937 gen(time(0));
struct node{int fix,l,r,sz;ll tag,val;
}t[N];
void pushup(int p){t[p].sz=t[t[p].l].sz+t[t[p].r].sz+1;
}
int newnode(ll val){tot++;t[tot].fix=gen(),t[tot].l=t[tot].r=t[tot].tag=0,t[tot].sz=1,t[tot].val=val;return tot;
}
void add(int p,ll x){if(!p)return;t[p].val+=x,t[p].tag+=x;
}
void pushdown(int p){if(t[p].tag)add(t[p].l,t[p].tag),add(t[p].r,t[p].tag),t[p].tag=0;
}
int merge(int x,int y){if(!x||!y)return x+y;if(t[x].fix>t[y].fix){pushdown(x);t[x].r=merge(t[x].r,y);pushup(x);return x;}else{pushdown(y);t[y].l=merge(x,t[y].l);pushup(y);return y;}
}
void split0(int rt,int &x,int &y,ll val){if(!rt){x=y=0;return;}pushdown(rt);if(t[rt].val>=val){x=rt;split0(t[x].r,t[x].r,y,val);pushup(x);}else{y=rt;split0(t[y].l,x,t[y].l,val);pushup(y);}
}
void split1(int rt,int &x,int &y,int val){if(!rt){x=y=0;return;}pushdown(rt);if(t[t[rt].l].sz+1<=val){x=rt;split1(t[x].r,t[x].r,y,val-t[t[rt].l].sz-1);pushup(x);}else{y=rt;split1(t[y].l,x,t[y].l,val);pushup(y);}
}
int rs(int x){while(t[x].r)x=t[x].r;return x;
}
int ls(int x){while(t[x].l)x=t[x].l;return x;
}
int cnt;
ll c[N];
void dfs(int x){pushdown(x);if(t[x].l)dfs(t[x].l);c[++cnt]=t[x].val;if(t[x].r)dfs(t[x].r);
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>T;while(T--){cin>>n>>str;for(int i=1;i<=n;i++)cin>>r[i];for(int i=1;i<=n;i++)cin>>b[i];rt=tot=0;ll sm=0;int c1=0;for(int i=1;i<=n;i++){if(r[i]<=b[i]){sm+=b[i];continue;}else if(str[i-1]=='1'){c1++,sm+=b[i];int x,y;split0(rt,x,y,r[i]-b[i]);rt=merge(x,merge(newnode(r[i]-b[i]),y));}else{sm+=r[i];int x,y;split1(rt,x,y,min(1ll*c1,r[i]-b[i]));if(!x||!y){add(x,-1);rt=x+y;}else{int _x=rs(x),_y=ls(y);if(t[_x].val==t[_y].val){ll val=t[_x].val;int a,b,c,d;split0(x,a,b,val+1);split0(y,c,d,val);add(a,-1),add(b,-1);rt=merge(merge(a,c),merge(b,d));}else{add(x,-1);rt=merge(x,y);}}}}cnt=0,dfs(rt);ll res=sm;for(int i=1;i<=c1;i++){sm+=c[i],res=max(res,sm);}cout<<res<<"\n";}
}
相关文章:

【学习笔记】CF1895G Two Characters, Two Colors
感谢grass8sheep提供的思路。 首先,我们可以用 D P DP DP解决这个问题。 设 f i , j f_{i,j} fi,j表示前 i i i个数中有 j j j个为 1 1 1的位置为红色的最大价值。则转移如下: f i , j ← f i − 1 , j b i f_{i,j}\gets f_{i-1,j}b_i fi,j←fi−…...
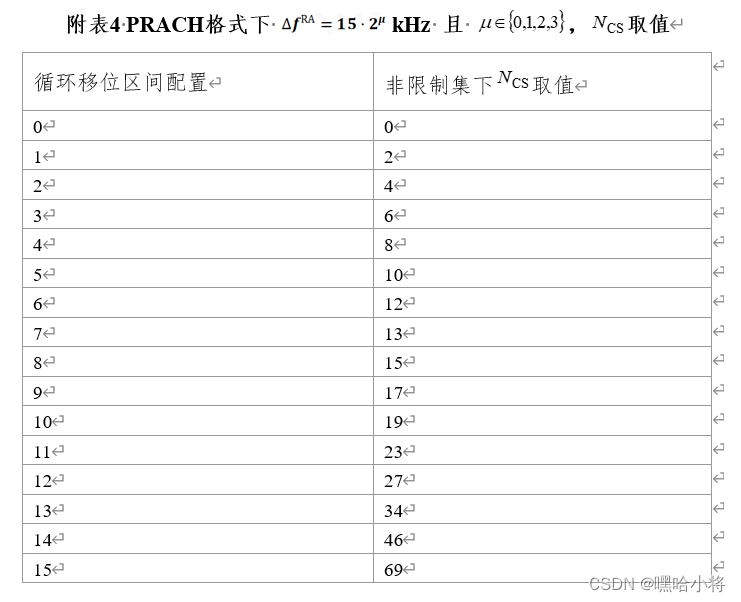
GZ035 5G组网与运维赛题第10套
2023年全国职业院校技能大赛 GZ035 5G组网与运维赛项(高职组) 赛题第10套 一、竞赛须知 1.竞赛内容分布 竞赛模块1--5G公共网络规划部署与开通(35分) 子任务1:5G公共网络部署与调试(15分) 子…...

基于SSM的教学管理系统(有报告)。Javaee项目。
演示视频: 基于SSM的教学管理系统(有报告)。Javaee项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring SpringMvc My…...
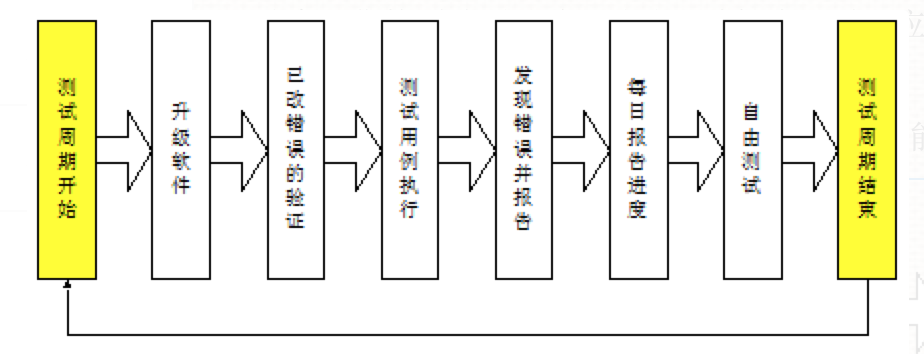
软件测试工作流程
流程体系介绍 在以往的项目工作中,我参与过,需求评审、测试计划制定、测试用例编写、测试用例执行、测试脚本编写、测试脚本的执行,进行回归测试、验收测试、编写阶段性测试报告等工作 需求分析,需求评审(RPD、产品原…...
高级文本编辑软件 UltraEdit mac中文版介绍说明
UltraEdit mac是一款在Windows系统中非常出名的文本编辑器, UltraEdit for mac对于IT程序猿来说,更是必不可少,可以使用UltraEdit编辑配置文件、查看16进制文件、代码高亮显示等,虽然Mac上已经有了很多优秀的文本编辑器࿰…...

python模块的介绍和导入
python模块的介绍和导入 概念 在Python中,每个Python代码文件都是一个模块。写程序时,我们可以将代码分散在不同的模块(文件)中,然后在一个模块中引用另一个模块的内容。 导入格式 1、在一个模块中引用(导入)另一个模块可以使用import语句…...
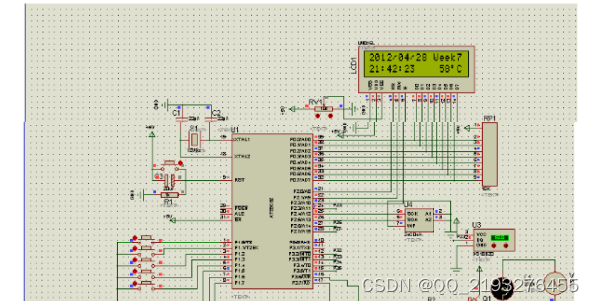
基于单片机的智能饮水机系统
收藏和点赞,您的关注是我创作的动力 文章目录 概要 一、系统设计方案分析2.1 设计功能及性能分析2.2设计方案分析 二、系统的硬件设计3.1 系统设计框图系统软件设计4.1 总体介绍原理图 四、 结论 概要 现在很多学校以及家庭使用的饮水机的功能都是比较单一的&#…...
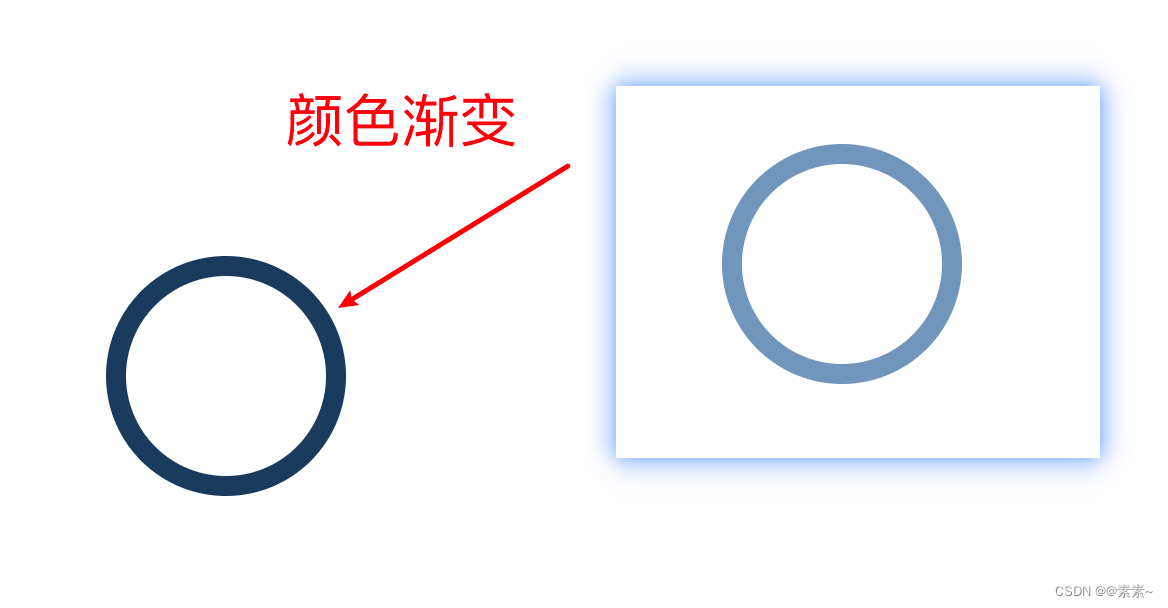
CSS画圆以及CSS实现动态圆
CSS画圆以及CSS实现动态圆 1. 先看基础(静态圆)1.1 效果如下:1.2 代码如下: 2. 动态圆2.1 一个动态圆2.1.1 让圆渐变2.1.2 圆渐变8秒后消失2.1.3 转动的圆(单个圆) 2.2 多个动态圆 1. 先看基础(…...
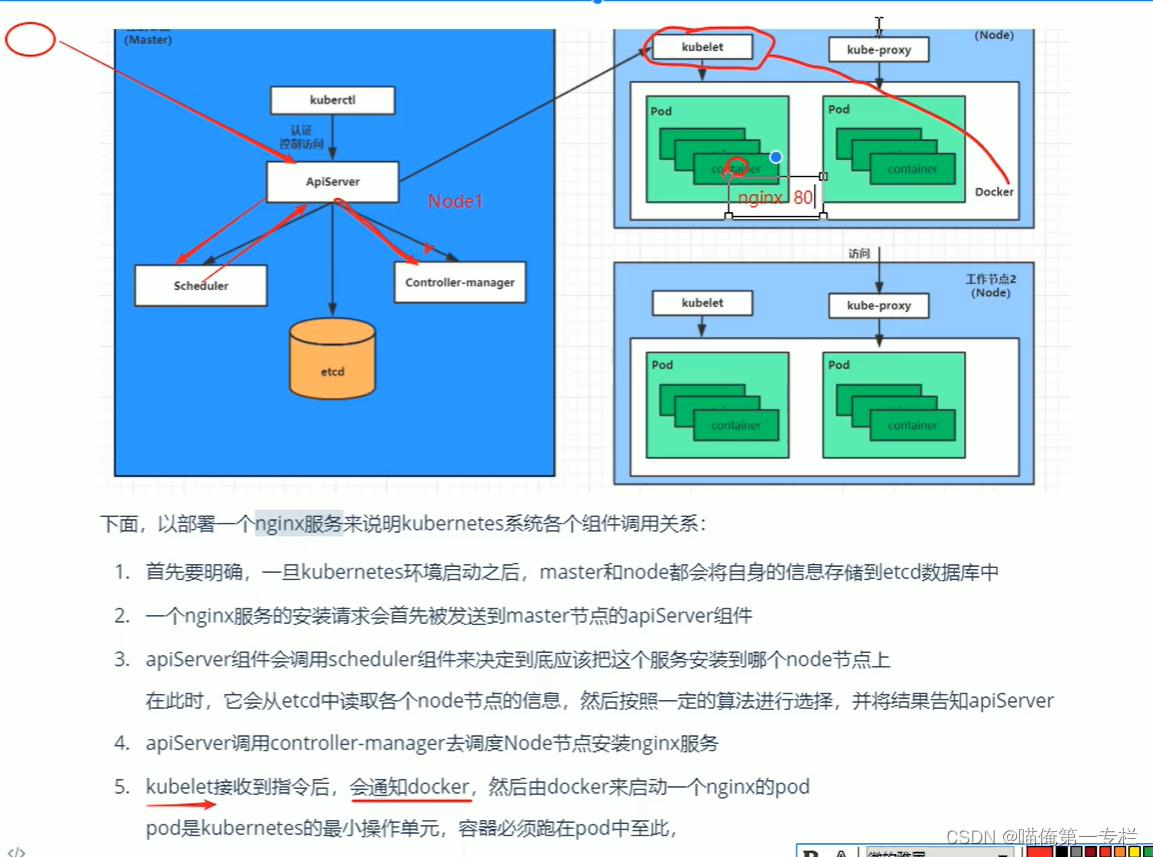
K8S知识点(一)
(1)应用部署方式转变 (2)K8S介绍 容器部署容易出现编排问题,为了解决就出现了大量的编排软件,这里将的是K8S编排问题的解决佼佼者 弹性伸缩:当流量从1000变为1200可以,自动开启一个…...
人工智能师求职面试笔试题及答案汇总
人工智能师求职面试笔试题及答案汇总 1.如何在Python中实现一个生成器? 答:在Python中,生成器是一种特殊类型的迭代器。生成器允许你在需要时才生成值,从而节省内存。生成器函数在Python中是通过关键字yield来实现的。例如&…...

【Windows-软件-FFmpeg】(01)通过CMD运行FFmpeg进行操作,快速上手
前言 通过"cmd"运行"ffmpeg"进行操作,快速上手; 实操 【实操一】 说明 使用"ffmpeg"来合并音频文件和视频文件 ; 环境 Windows 11 专业版(22621.2428); 代码 …...

Spring Data Redis + RabbitMQ - 基于 string 实现缓存、计数功能(同步数据)
目录 一、Spring Data Redis 1.1、缓存功能 1.1.1、分析 1.1.2、案例实现 1.1.3、效果演示 1.2、计数功能(Redis RabbitMQ) 1.2.1、分析 1.2.2、案例实现 一、Spring Data Redis 1.1、缓存功能 1.1.1、分析 使用 redis 作为缓存, M…...

Facebook Developer 的 HashCode
在 Android 中,您可以使用 Facebook SDK 提供的工具来生成您的应用程序的哈希码(hash code),以便在 Facebook 开发者帐户中配置您的应用程序。 要生成哈希码,您可以使用以下步骤: 打开终端或命令提示符&am…...

下载使用 ant design Pro 中遇到的一些问题
文章目录 npm 版本问题在idea终端输入命令报错:error:0308010C:digital envelope routines::unsupported npm 版本问题 npm v9.6.3 is known not to run on Node.js v19.9.0. This version of npm supports the following node versions: ^14.17.0 || ^16.13.0 || …...
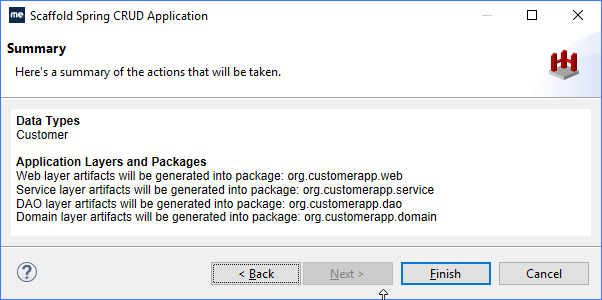
「Java开发指南」如何用MyEclipse搭建Spring MVC应用程序?(一)
本教程将指导开发者如何生成一个可运行的Spring MVC客户应用程序,该应用程序实现域模型的CRUD应用程序模式。在本教程中,您将学习如何: 从数据库表的Scaffold到现有项目部署搭建的应用程序 使用Spring MVC搭建需要MyEclipse Spring或Bling授…...
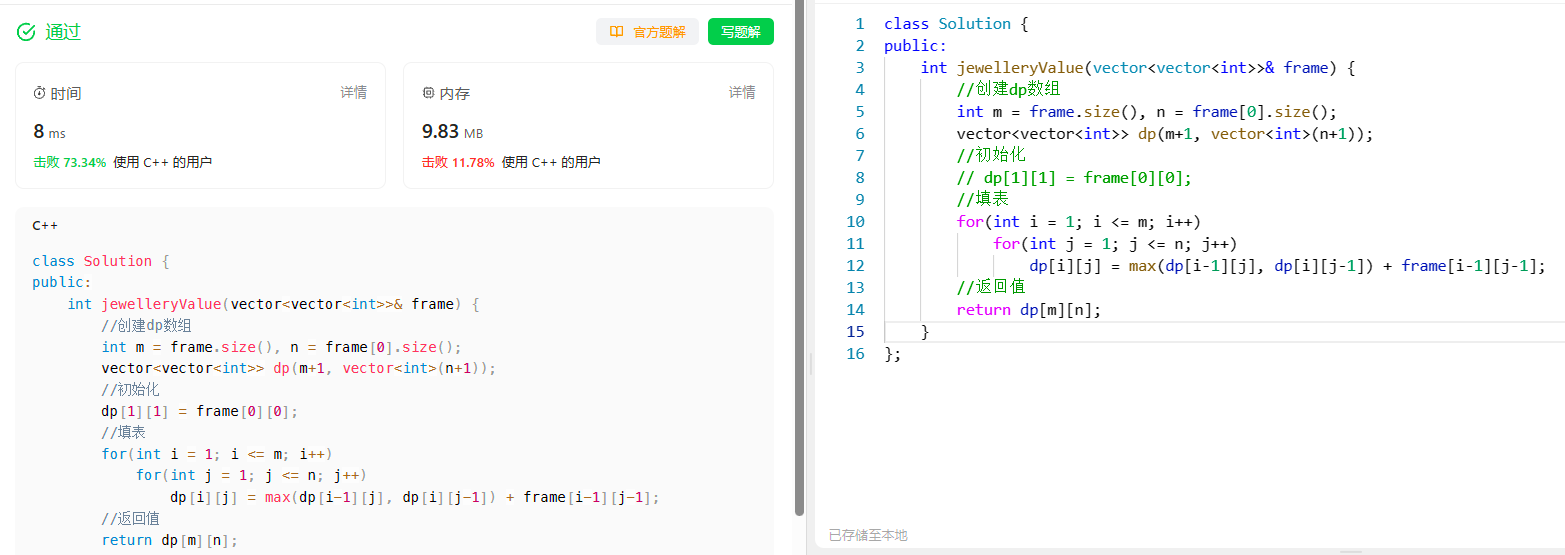
[动态规划] (七) 路径问题:LCR 166.剑指offer 47. 珠宝的最高价值
[动态规划] (七) 路径问题:LCR 166./剑指offer 47. 珠宝的最高价值 文章目录 [动态规划] (七) 路径问题:LCR 166./剑指offer 47. 珠宝的最高价值题目解析解题思路状态表示状态转移方程初始化和填表顺序 返回值代码实现总结 LCR 166. 珠宝的最高价值 题目…...

Mysql进阶-SQL优化篇
插入数据 insert 我们需要一次性往数据库表中插入多条记录,可以从以下三个方面进行优化。 批量插入数据 一条insert语句插入多个数据,但要注意,每个insert语句最好插入500-1000行数据,就得重新写另一条insert语句 Insert into…...
VueI18n中英文切换 vue2.0
1: npm install --save vue-i18n8.0.0 (版本不要高了,不然报错) 2:创建相关文件 3:main.js文件配置 //i18n插件 import VueI18n from vue-i18n // element-ui多语言文件 import locale from element-ui/lib/locale;…...

VUE组件间通信的七种方式
目录 1、 props / $emit (1)父组件向子组件传值(props的用法) (2)子组件向父组件传递数据($emit的用法) 2、ref / $refs 用法: 3、eventBus事件总线($e…...

问chatgpt最近生活的困难
你知道吗,因为我做的所有的事情没有任何目的性,所以曾经过的很好,这种很好是一种逃避式的好,怎么说呢?遇到困难了,那就不做了,换下一个项目。比如打游戏,如果我这局玩王者荣耀&#…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
