追梦之旅【数据结构篇】——详解C语言实现二叉树
详解C语言实现二叉树~😎
- 前言🙌
- 什么是二叉树?
- 二叉树的性质总结:
- 整体实现内容分析💞
- 1.头文件的编写:🙌
- 2.功能文件的编写:🙌
- 1)前序遍历的数值来创建树——递归函数实现 😊
- 2)求树的高度函数实现 😊
- 3)求叶子数函数实现 😊
- 4)求树的总结点个数函数实现 😊
- 5)前序遍历二叉树实现 😊
- 6)中序遍历二叉树实现 😊
- 7)后序遍历二叉树实现 😊
- 8)删除二叉树函数实现 😊
- 3.测试文件编写::🙌
- 总结撒花💞

😎博客昵称:博客小梦
😊最喜欢的座右铭:全神贯注的上吧!!!
😊作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
😘博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,手把手带领大家详解C语言实现二叉树~ 利用二叉链式存储结构来完成二叉树的实现,并完成叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。都是精华内容,可不要错过哟!!!😍😍😍
什么是二叉树?
满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树的性质总结:
- 二叉树中,第 i 层最多有 2^( i-1)个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2^K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
二叉树又可以分类为许多不同的二叉树:

整体实现内容分析💞
- 利用二叉链式存储结构来完成二叉树的实现,并完成叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。
- 采用递归的思想,先是malloc开辟结点空间,然后给结点赋值,然后递归左子树然后递归右子树。这里用*表示空。最后返回生成的root指针的地址求高度,采用后序遍历的思想。
- 相当于求左右子树结点高度的最大值。每次递归加1就是计算结点数。求叶子总数时先求出左子树的叶子数再加上右子树的叶子数。求总结点数时这里直接递归计算出左子树和右子树的总结点数,每次加1表示遍历的节点数计算。然后就是前中后序的实现,这里也是用到递归的思想,最后便是将数销毁掉,malloc生成的空间要用free手动销毁。
1.头文件的编写:🙌
头文件的编写的整体思路分析:
这里用的是二叉链式存储的实现。首先是定义结构体,然后是对求叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。
#pragma once
#include"stdio.h"
#include"stdlib.h"
typedef int datatype;
typedef struct node
{datatype data;struct node* lchild, * rchild;
}tree;
tree* Creatbitree();
int Depthbitree(tree* T);
int Leaf_count(tree* T);
int Countbitree(tree* T);
int Preorder(tree* T);
int Inorder(tree* T);
int Postorder(tree* T);
tree* Delete(tree* T);2.功能文件的编写:🙌
1)前序遍历的数值来创建树——递归函数实现 😊
编写的整体思路分析:
采用递归的思想,先是malloc开辟结点空间,然后给结点赋值,然后递归左子树然后递归右子树。这里用*表示空。最后返回生成的root指针的地址
#include"BinaryTree.h"
tree* Creatbitree()//前序遍历的数值来创建树——递归
{char ch;tree* root;scanf("%c", &ch);//用于接收输入的数值 if (ch == '*') return NULL;//用*来判断是否为空 else {root = (tree*)malloc(sizeof(tree));root->data = ch;//赋值 root->lchild = Creatbitree();//左子树 root->rchild = Creatbitree();//右子树 }return root;
}
2)求树的高度函数实现 😊
编写的整体思路分析:
这里求高度,采用后序遍历的思想。相当于求左右子树结点高度的最大值。每次递归加1 就是计算结点数。
int Depthbitree(tree* T)//测量树的深度
{if (T == NULL) return 0;else {int leftheighter = Depthbitree(T->lchild);int rightheighter = Depthbitree(T->rchild);return (leftheighter > rightheighter ? leftheighter + 1 : rightheighter + 1);}
}3)求叶子数函数实现 😊
编写的整体思路分析:
代码上已表明算法思想,先求出左子树的叶子数再加上右子树的叶子数。
int Leaf_count(tree* T)//测量叶子的数量
{if (T == NULL) return 0;else if (!T->lchild && !T->rchild)//如果左右结点都为空则他就是叶子结点 return 1;else return Leaf_count(T->lchild) + Leaf_count(T->rchild);
}4)求树的总结点个数函数实现 😊
编写的整体思路分析:
这里直接递归计算出左子树和右子树的总结点数,每次加1表示遍历的节点数计算。
int Countbitree(tree* T) //测量总的结点个数
{if (T == NULL)return 0;else {return Countbitree(T->lchild) + Countbitree(T->rchild)+1;}
}5)前序遍历二叉树实现 😊
int Preorder(tree* T)//前序遍历序列 (根左右)
{if (T == NULL)return 0;else {printf("%c ", T->data);//先输出根节点 Preorder(T->lchild);Preorder(T->rchild);}
}6)中序遍历二叉树实现 😊
int Inorder(tree* T)//中序遍历序列 (左根右)
{if (T == NULL)return 0;else {Inorder(T->lchild);//先输出左孩子 printf("%c ", T->data);Inorder(T->rchild);}
}7)后序遍历二叉树实现 😊
int Postorder(tree* T)//后序遍历序列 (左右根)
{if (T == NULL)return 0;else {Postorder(T->lchild);//先输出左孩子 Postorder(T->rchild);printf("%c ", T->data);}
}8)删除二叉树函数实现 😊
tree* Delete(tree* T)//删除树
{if (T->lchild)Delete(T->lchild);else if (T->rchild)Delete(T->rchild);elsefree(T);
}3.测试文件编写::🙌
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"main()
{tree* T;T = (tree*)malloc(sizeof(tree));T->lchild = NULL;T->rchild = NULL;printf("请输入树的前序遍历序列\n");T = Creatbitree();int n = Depthbitree(T);int m = Leaf_count(T);int l = Countbitree(T);printf("树创建完成\n");printf("前序输出为\n");printf("\t\t");Preorder(T);printf("\n中序输出为\n");printf("\t\t");Inorder(T);printf("\n后序输出为\n");printf("\t\t");Postorder(T);printf("\n高度%d\n叶子%d\n总结点%d\n", n, m, l);Delete(T);printf("删除成功");
}功能测试结果展示图:

总结撒花💞
本篇文章旨在分享详解C语言实现二叉树。希望大家通过阅读此文有所收获!本次主要是对二叉树的实现,这里只要用到的思想是递归,这也是难点所在。这就要需要画图帮忙辅助理解,递归的具体每一步是如何执行的需要分析清楚。在创建树的时候可以采用前序遍历思想创建,这种思想创建是比较好理解的,也可以用其他思想创建,相对比较难理解一点。以及区分好前中后序遍历的思想,然后再编写代码。
😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘
相关文章:

追梦之旅【数据结构篇】——详解C语言实现二叉树
详解C语言实现二叉树~😎前言🙌什么是二叉树?二叉树的性质总结:整体实现内容分析💞1.头文件的编写:🙌2.功能文件的编写:🙌1)前序遍历的数值来创建树——递归函…...

独家 | Gen-1——可以改变视频风格的AI模型
翻译:吴振东校对:张睿毅本文约1000字,建议阅读3分钟 本文简单介绍了Runway公司的发展史,以及他们新推出的生成式AI模型Gen-1,可用于通过应用文本提示或者参考图像所指定的任意风格,将现有视频转换为新视频。…...
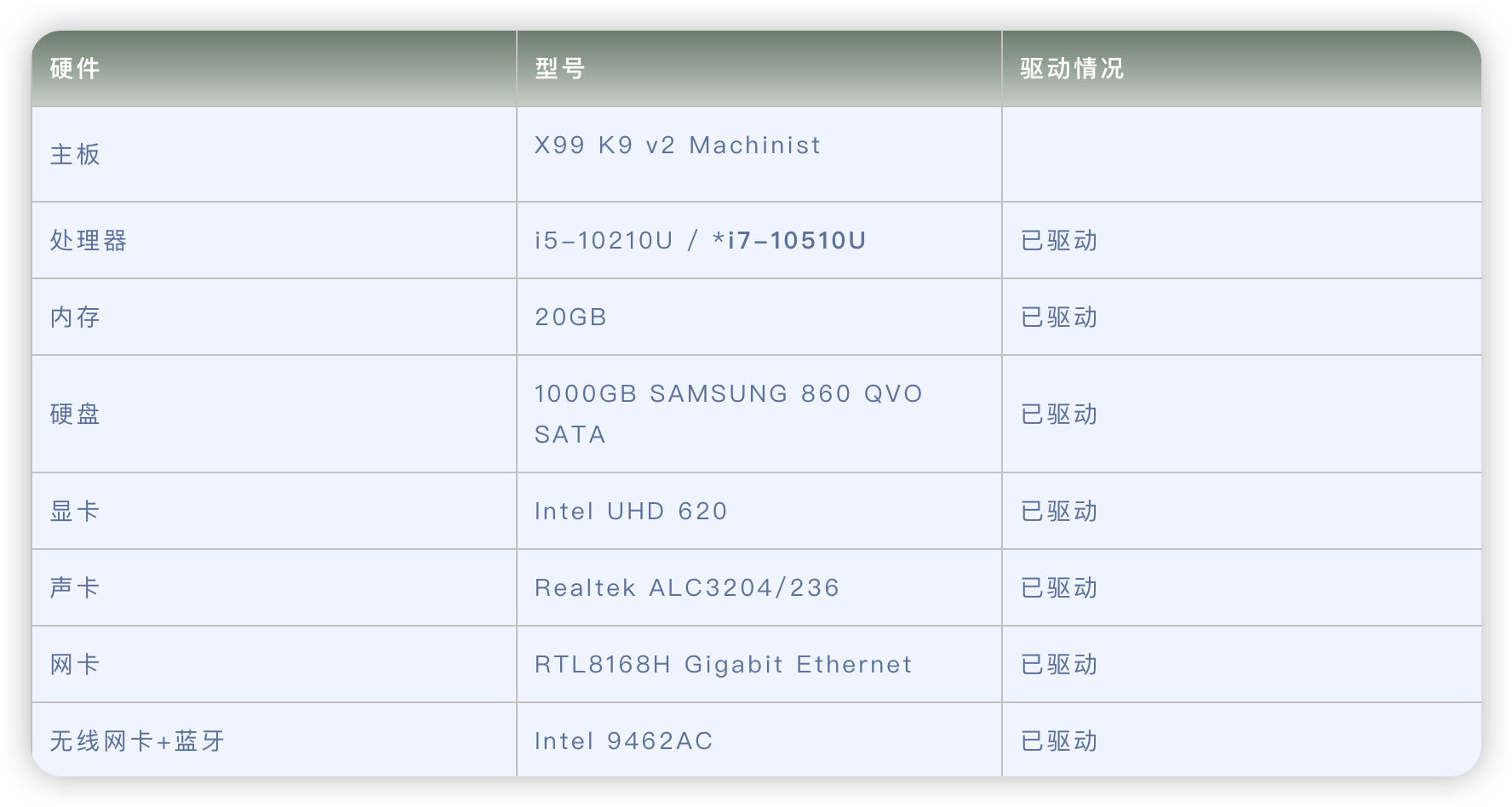
戴尔dell inspiron-5598电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板X99 K9 v2 Machinist处理器i5-10210U / *i7-10510U已驱动内存20GB已驱动硬盘1000GB SAMSUNG 860 QVO SATA已驱动显卡Intel UHD 620已驱动声卡Realtek ALC3204/236已驱动网卡RTL8168H Gigabit Ethernet已…...
3.2 网站图的爬取路径
深度优先与广度优先方法都是遍历树的一种方法,但是网站的各个网页 之间的关系未必是树的结构,它们可能组成一个复杂的图形结构,即有回路。如果在前面的网站中每个网页都加一条Home的语句,让每个网页都能回到主界面,那么…...

《SQL基础》12. SQL优化
SQL优化SQL优化数据插入insert优化大批量插入数据主键优化order by优化group by优化limit优化count优化count用法update优化SQL优化 数据插入 insert优化 如果我们需要一次性往数据库表中插入多条记录,可以从以下三个方面进行优化。 批量插入手动控制事务主键顺…...

fork之后是子进程先执行还是父进程先执行
CFS(完全公平调度器)是Linux内核2.6.23版本开始采用的进程调度器,它的基本原理是这样的:设定一个调度周期(sched_latency_ns),目标是让每个进程在这个周期内至少有机会运行一次,换一种说法就是每个进程等待CPU的时间最长不超过这个…...
)
2023年java初级面试题(5道)
一、两个对象值相同(x.equals(y) true),但却可有不同的hash code,这句话对不对?答:不对,如果两个对象x和y满足x.equals(y) true,它们的哈希码(hash code)应当相同。Java对于eqauls…...
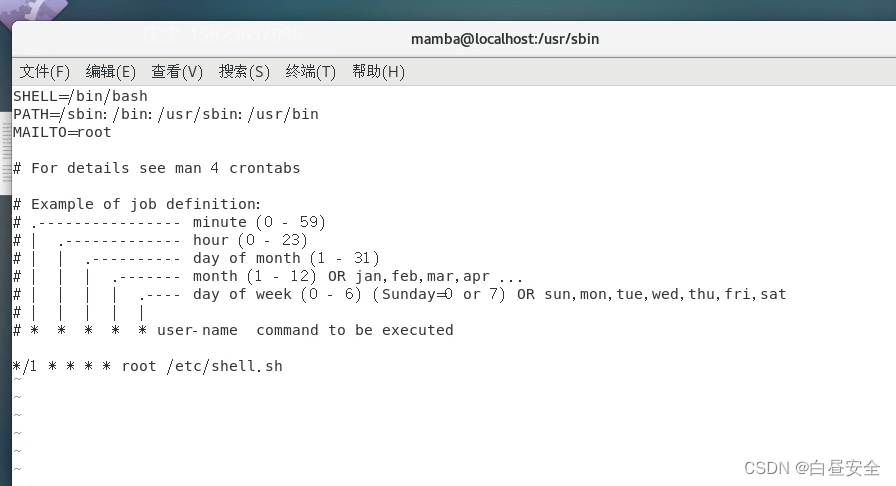
【内网安全】——Linux权限维持
作者名:白昼安全主页面链接: 主页传送门创作初心: 以后赚大钱座右铭: 不要让时代的悲哀成为你的悲哀专研方向: web安全,后渗透技术每日鸡汤: 钱至少对于现在的我来说,的确是万能的在…...

Linux 真实使用内存计算
获取Linux内存信息,可通过cat /proc/meminfo查看,比如,Ubuntu 20.04.5 LTS上会显示以下信息: leoyaDESKTOP-LMR:~$ cat /proc/meminfo MemTotal: 16017572 kB MemFree: 15637472 kB MemAvailable: 15533140 kB Bu…...
Unity Jobsystem ECS
简介随着ECS的加入,Unity基本上改变了软件开发方面的大部分方法。ECS的加入预示着OOP方法的结束。随着实体组件系统ECS的到来,我们在Unity开发中曾使用的大量实践方法都必须进行改变以适应ECS,也许不少人需要些时间适应ECS的使用,…...

Java中创建线程有哪几种方式
1.继承Thread类 总结:通过继承 Thread 类,重写 run() 方法,而不是 start() 方法 Thread 类底层实现 Runnable 接口类只能单继承 接口可以多继承2.实现Runnable接口 总结:通过实现 Runnable 接口,实现 run() 方法,依然…...
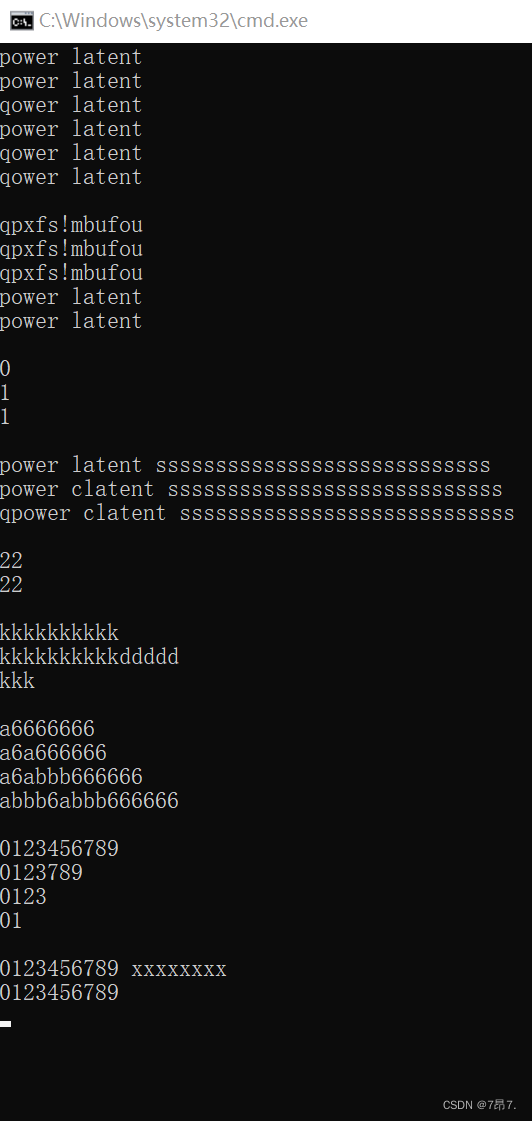
C++【string类用法详细介绍string类模拟实现解析】
文章目录string 类用法介绍及模拟实现一、string介绍二、string类常用接口1. string类对象的常见构造接口2.string类对象的常见容量接口3.string类对象的常见修改接口4. string类对象的常见访问及遍历接口5.string其他接口1.不常用查找接口2.字符替换3.字符串拼接4.字符串排序5…...

常见的开发模型和测试模型
软件的生命周期软件开发阶段的生命周期需求分析->计划->设计->编码->测试->运维软件测试阶段的生命周期需求分期->测试计划->测试设计与开发->执行测试->测试评估开发模型瀑布模型可以看到,这个模型和我们上面的软件开发生命周期很相似采用的是线性…...

印度和印度尼西亚有什么关系吗?
印度和印度尼西亚,这两个国家很多人都比较熟悉。因为两国都是人口大国,而且经济总量也比较高,在全球还是有很大影响的。不过很多人刚看到这两个国家的时候,都会觉得这两个国家肯定有什么关系,要不然国名也不会这么像。…...
单调栈(C/C++)
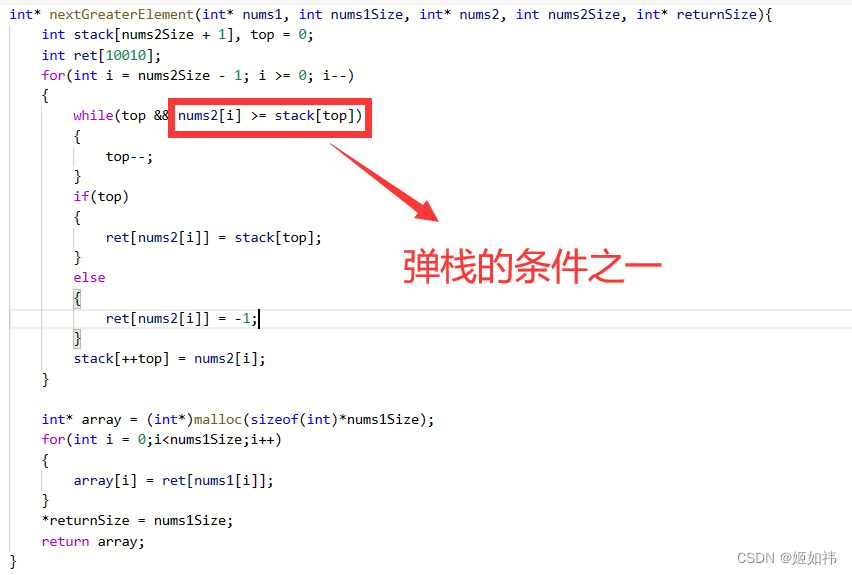
目录 1. 单调栈的定义 2. 单调栈的常见用途 3. 案例分析 3.1 暴力解法 3.2 单调栈 4. 单调栈总结 1. 单调栈的定义 单调栈顾名思义,就是栈内的元素是单调的。根据栈内元素的单调性的不同,可以分为: 单调递增栈:栈内元素是单…...

算法设计与智能计算 || 专题一: 算法基础
专题一: 算法基础 文章目录专题一: 算法基础1. 算法的定义及特点1.1 算法的基本特征1.2 算法的基本要素1.3 算法的评定2 算法常见执行方法2.1 判断语句2.2 循环语句2.3 综合运用3. 计算复杂度4. 代码的重用5. 类函数的定义与使用5.1 定义类5.2 调用类函数1. 算法的定义及特点 …...

用javascript分类刷leetcode13.单调栈(图文视频讲解)
239. 滑动窗口最大值 (hard) 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1: 输入:nums [1,…...

英语基础语法学习(B站英语电力公司)
1. 句子结构 五大基本句型: 主谓主谓宾主谓宾宾主谓宾宾补主系表 谓语: 一般来说,谓语是指主语发出的动作。(动词)但是很多句子是没有动作的,但是还是必须要有谓语。(此时需要be动词&#x…...
【计算机网络】网络层IP协议
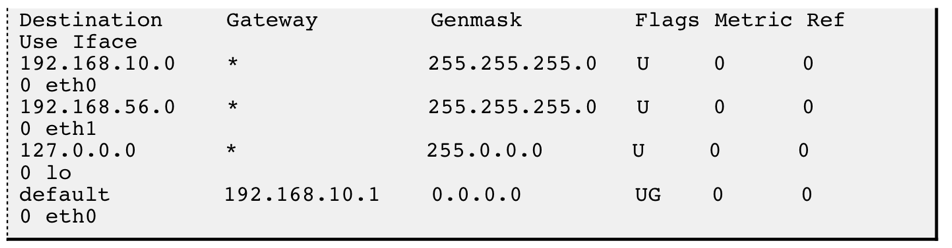
文章目录一、认识IP协议二、IP协议头部格式三、IP地址划分1. IP地址分类2. 子网划分四、IP地址数量危机1. IP地址的数量限制2. NAT技术五、私网IP和公网IP六、路由1. 认识路由2. 路由表生成算法一、认识IP协议 IP协议是Internet Protocol(互联网协议)的…...

Eclipse快捷键大全
编辑类快捷键Ctrl1: 快速修复(最经典的快捷键, 可以解决很多问题, 比如import类、try catch包围等)CtrlShiftF: 格式化当前代码CtrlShiftM: 添加类的import导入CtrlShiftO: 组织类的导入(既有CtrlShiftM的作用,又可以去除没用的导入, 一般用这个导入包)CtrlY: 重做(与CtrlZ相反…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

