洛谷 P1359 租用游艇
题目链接
P1359 租用游艇
普及
题目描述
长江游艇俱乐部在长江上设置了 n n n 个游艇出租站 1 , 2 , 3 , . . . , n 1,2,3,...,n 1,2,3,...,n,游客可在这些游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站 i i i 到游艇出租站 j j j 之间的租金为 r ( i , j ) ( 1 ≤ i ≤ j ≤ n ) r(i,j) \quad (1 \leq i \leq j \leq n) r(i,j)(1≤i≤j≤n) 。
请计算出从 出租站 1 1 1 到 出租站 n n n 所需的最少租金。
输入格式
第一行中有一个正整数 n n n ,表示有 n n n 个游艇出租站。
接下来的 n − 1 n - 1 n−1 行是一个半矩阵 r ( i , j ) ( 1 ≤ i ≤ j ≤ n ) r(i,j) \quad (1 \leq i \leq j \leq n) r(i,j)(1≤i≤j≤n)。
输入格式
输出计算出的从游艇出租站 1 1 1 到游艇出租站 n n n 所需的最少租金。
数据范围
n ≤ 200 n≤200 n≤200,保证计算过程中任何时刻数值都不超过 1 0 6 10^6 106 。
示例1:
输入:
3
5 15
7
输出:
12
解法:贪心
我们定义邻接矩阵 g g g, g [ i ] [ j ] g[i][j] g[i][j] 记录的是 出租站 i i i 到 出租站 j j j 的距离。
我们定义 f [ i ] f[i] f[i] 表示从 出租站 1 1 1 到 出租站 i i i 所需要的最小租金。按照定义,我们最终返回的答案就是 f [ n ] f[n] f[n]。
我们可以得出如下状态转移方程:
f [ i ] = m i n { f [ i ] , f [ j ] + g [ j ] [ i ] } ( 1 ≤ j < i ) f[i] = min \{ f[i] , f[j] + g[j][i] \} \quad (1 \leq j < i) f[i]=min{f[i],f[j]+g[j][i]}(1≤j<i)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
C++代码:
#include<iostream>
#include<vector>using namespace std;const int N = 210;
int g[N][N];void solve(){int n;cin>>n;for(int i = 1;i < n;i++){for(int j = i + 1;j <= n;j++){cin>>g[i][j];}}vector<int> f(n + 1 , 1e9);f[1] = 0;for(int i = 2;i <= n;i++){for(int j = 1;j < i;j++) f[i] = min(f[i] , f[j] + g[j][i]);}cout<<f[n]<<'\n';
}int main(){solve();return 0;
}
相关文章:

洛谷 P1359 租用游艇
题目链接 P1359 租用游艇 普及 题目描述 长江游艇俱乐部在长江上设置了 n n n 个游艇出租站 1 , 2 , 3 , . . . , n 1,2,3,...,n 1,2,3,...,n,游客可在这些游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站 i i i 到游艇出租站…...

springboot中没有主清单属性解决办法
在执行一个 spring boot 启动类时,提示 没有主清单属性 一般这个问题是没加 spring-boot-maven-plugin 插件的问题,但是项目中已经加了 <build><plugins><plugin><groupId>org.springframework.boot</groupId><artifa…...

C/C++ static关键字详解(最全解析,static是什么,static如何使用,static的常考面试题)
目录 一、前言 二、static关键字是什么? 三、static关键字修饰的对象是什么? 四、C 语言中的 static 🍎static的C用法 🍉static的重点概念 🍐static修饰局部变量 💦static在修饰局部变量和函数的作用 &a…...
windwos10搭建我的世界服务器,并通过内网穿透实现联机游戏Minecraft
文章目录 1. Java环境搭建2.安装我的世界Minecraft服务3. 启动我的世界服务4.局域网测试连接我的世界服务器5. 安装cpolar内网穿透6. 创建隧道映射内网端口7. 测试公网远程联机8. 配置固定TCP端口地址8.1 保留一个固定tcp地址8.2 配置固定tcp地址 9. 使用固定公网地址远程联机 …...
【实战Flask API项目指南】之七 用JWT进行用户认证与授权
实战Flask API项目指南之 用JWT进行用户认证与授权 本系列文章将带你深入探索实战Flask API项目指南,通过跟随小菜的学习之旅,你将逐步掌握 Flask 在实际项目中的应用。让我们一起踏上这个精彩的学习之旅吧! 前言 当小菜踏入Flask后端开发…...
鸿蒙LiteOs读源码教程+向LiteOS中添加一个简单的基于线程运行时的短作业优先调度策略
【⭐据说点赞收藏的都会收获好运哦👍】 一、鸿蒙Liteos读源码教程 鸿蒙的源码是放在openharmony文件夹下,openharmony下的kernel文件夹存放操作系统内核的相关代码和实现。 内核是操作系统的核心部分,所以像负责:资源管理、任…...

axios的使用与封装详细教程
目录 一、axios使用方式二、axios在main.js配置 一、axios使用方式 在 Spring Boot Vue 的项目中使用 Axios,你需要在 Vue 项目中安装 Axios 库,因为 Axios 是一个前端 JavaScript 库,用于发送 HTTP 请求和处理响应数据,而与 Sp…...
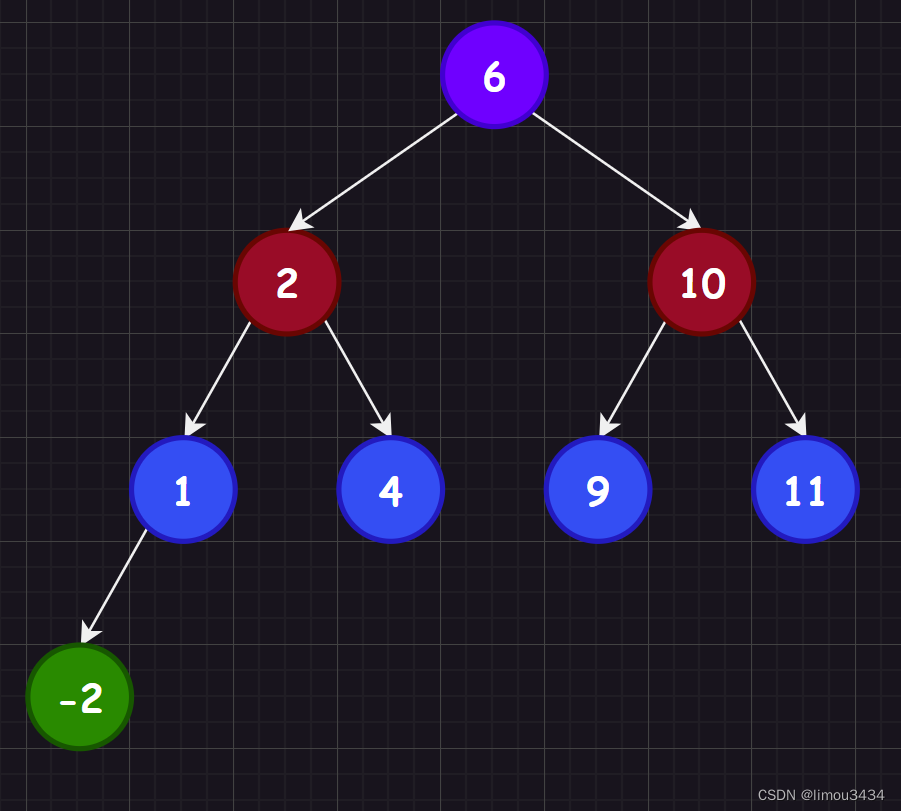
C++二叉搜索树
本章主要是二叉树的进阶部分,学习搜索二叉树可以更好理解后面的map和set的特性。 1.二叉搜索树概念 二叉搜索树的递归定义为:非空左子树所有元素都小于根节点的值,非空右子树所有元素都大于根节点的值,而左右子树也是二叉搜索树…...
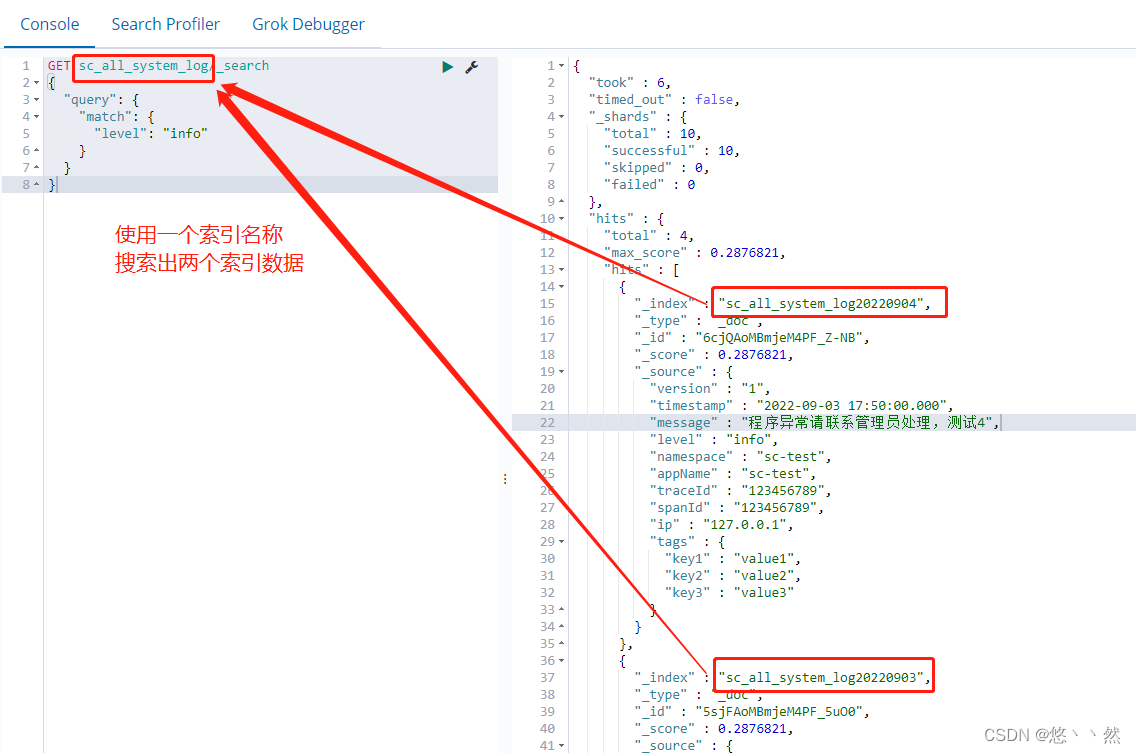
elasticsearch索引按日期拆分
1.索引拆分原因 如果单个索引数据量过大会导致搜索变慢,而且不方便清理历史数据。 例如日志数据每天量很大,而且需要定期清理以往日志数据。例如原索引为sc_all_system_log,现按天拆分索引sc_all_system_log20220902,sc_all_syste…...

纯python实现大漠图色功能
大漠图色是一种自动化测试工具,可以用于识别屏幕上的图像并执行相应的操作。在Python中,可以使用第三方库pyautogui来实现大漠图色功能。具体步骤如下: 安装pyautogui库:在命令行中输入pip install pyautogui。导入pyautogui库&a…...

debounce and throtlle
debounce // 核心:单位时间内触发>1 则只执行最后一次。//excutioner 可以认为是执行器。执行器存在则清空,再赋值新的执行器。function debounce(fn, delay 500) {let excutioner null;return function () {let context this;let args arguments…...

四、数据库系统
数据库系统(Database System),是由数据库及其管理软件组成的系统。数据库系统是为适应数据处理的需要而发展起来的一种较为理想的数据处理系统,也是一个为实际可运行的存储、维护和应用系统提供数据的软件系统,是存储介…...
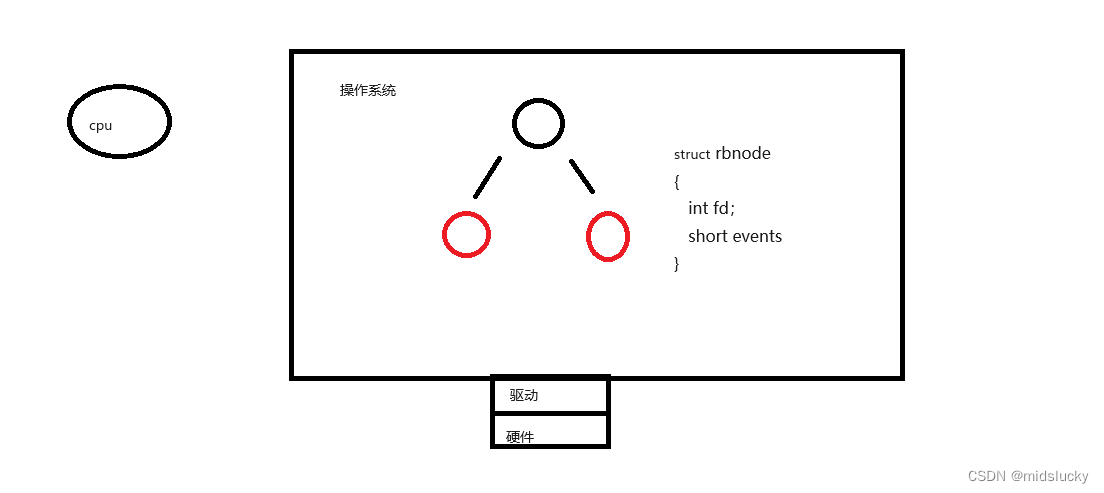
Linux中的高级IO
文章目录 1.IO1.1基本介绍1.2基础io的低效性1.3如何提高IO效率1.4五种IO模型1.5非阻塞模式的设置 2.IO多路转接之Select2.1函数的基本了解2.2fd_set理解2.3完整例子代码(会在代码中进行讲解)2.4优缺点 3.多路转接之poll3.1poll函数的介绍3.2poll服务器3.…...
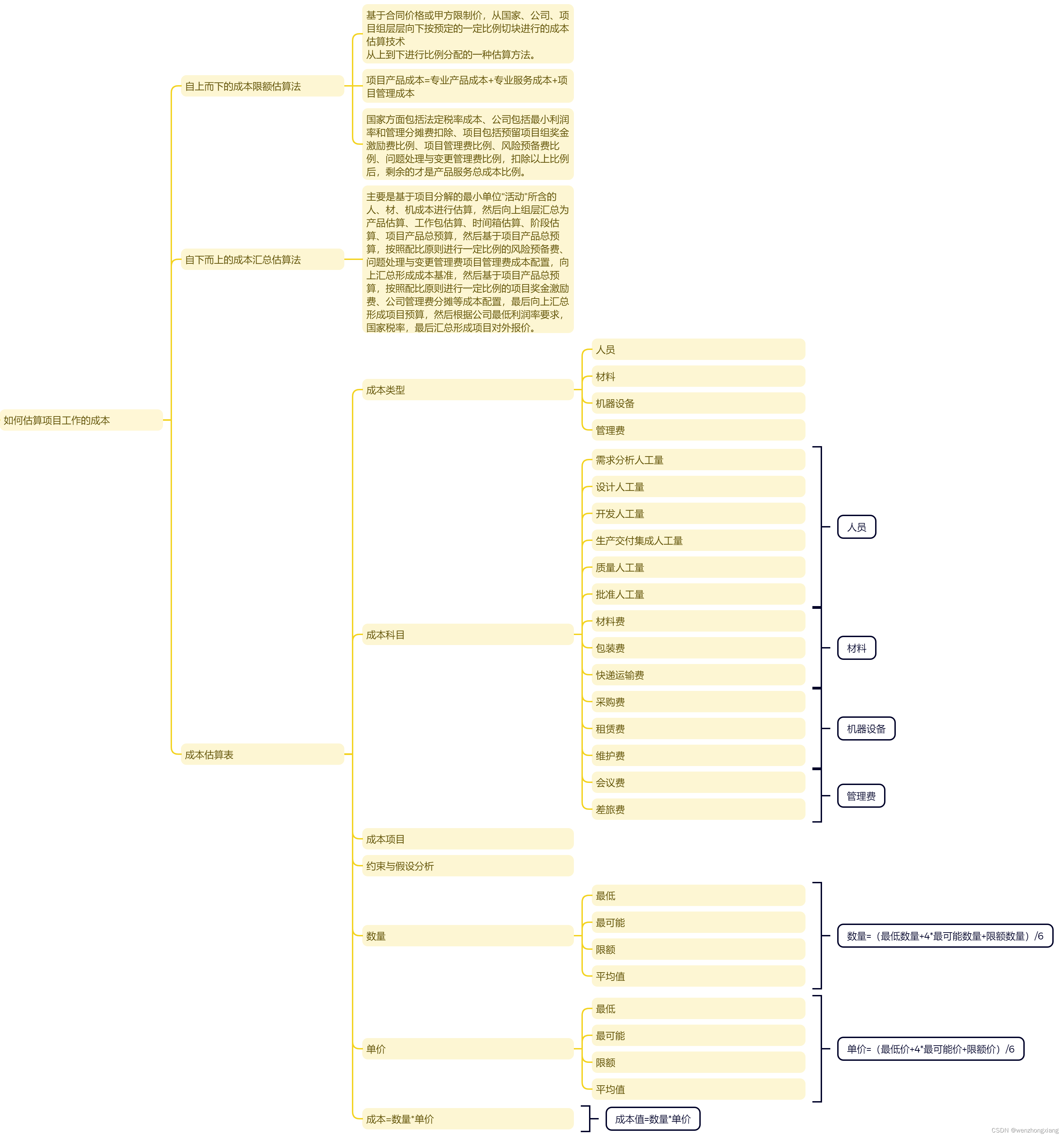
项目管理之如何估算项目工作成本
在项目管理中,如何估算项目工作成本是一个关键问题。为了解决这个问题,我们可以采用自上而下的成本限额估算法和自下而上的成本汇总估算法。这两种方法各有优缺点,但都可以帮助我们准确地估算项目工作成本。 自上而下的成本限额估算法 自上…...

Redis主从复制基础概念
Redis主从复制:提高数据可用性和性能的策略 一、概述 Redis主从复制是一种常用的高可用性策略,通过将数据从一个Redis服务器复制到另一个或多个Redis服务器上,以提高数据的可用性和读取性能。当主服务器出现故障时,可以快速地切…...
图数据库Neo4j概念、应用场景、安装及CQL的使用
一、图数据库概念 引用Seth Godin的说法,企业需要摒弃仅仅收集数据点的做法,开始着手建立数据之间的关联关系。数据点之间的关系甚至比单个点本身更为重要。 传统的**关系数据库管理系统(RDBMS)**并不擅长处理数据之间的关系,那些表状数据模…...
: RIP原理与配置)
路由器基础(四): RIP原理与配置
路由信息协议 (Routing Information Protocol,RIP) 是最早使用的距离矢量路由协议。因为路由是以矢量(距离、方向)的方式被通告出去的,这里的距离是根据度量来决定的,所以叫“距离矢量”。 距离矢量路由算法是动态路由算法。它的工作流程是:…...

红外遥控开发RK3568-PWM-IR
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1.红外遥控的发送接收工作原理2.红外协议3.红外遥控系统框图4.遥控器添加方法4.1 记录键值4.2 添加键值总结前言 提示:这里可以添加本文要记录的大概内容: 1.红外遥控的发送接收工作原理 …...

go-sync-mutex
Sync Go 语言作为一个原生支持用户态进程(Goroutine)的语言,当提到并发编程、多线程编程时,往往都离不开锁这一概念。锁是一种并发编程中的同步原语(Synchronization Primitives),它能保证多…...
高并发系统设计
高并发系统通用设计方法 Scala-out 横向扩展,分散流量,分布式集群部署 缺点:引入复杂度,节点之间状态维护,节点扩展(上下线) Scala-up 提升单机性能,比如增加内存,增…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
