Acwing 蓝桥杯 第一章 递归与递推
我上周在干什么,感觉我上周啥也没训,本来两天一次的vp也没v
很寄啊,再这样下去真不行了
先总结一下如何爆搜:
先去确定好枚举的对象
枚举的对象很重要!!这直接影响了复杂度
然后就是去想递归树就好了
一、确定状态:
状态分为全局变量和局部变量
考虑状态时去考虑三样东西:
阶段(即深度),阶段作为出口
影响决策的因素(全局or局部)
要维护的答案
二、枚举决策+加限定条件
三、确定出口(根据阶段)
那么我们怎么去考虑复杂度:考虑每一层树的结点个数*每个结点的复杂度
92. 递归实现指数型枚举 - AcWing题库
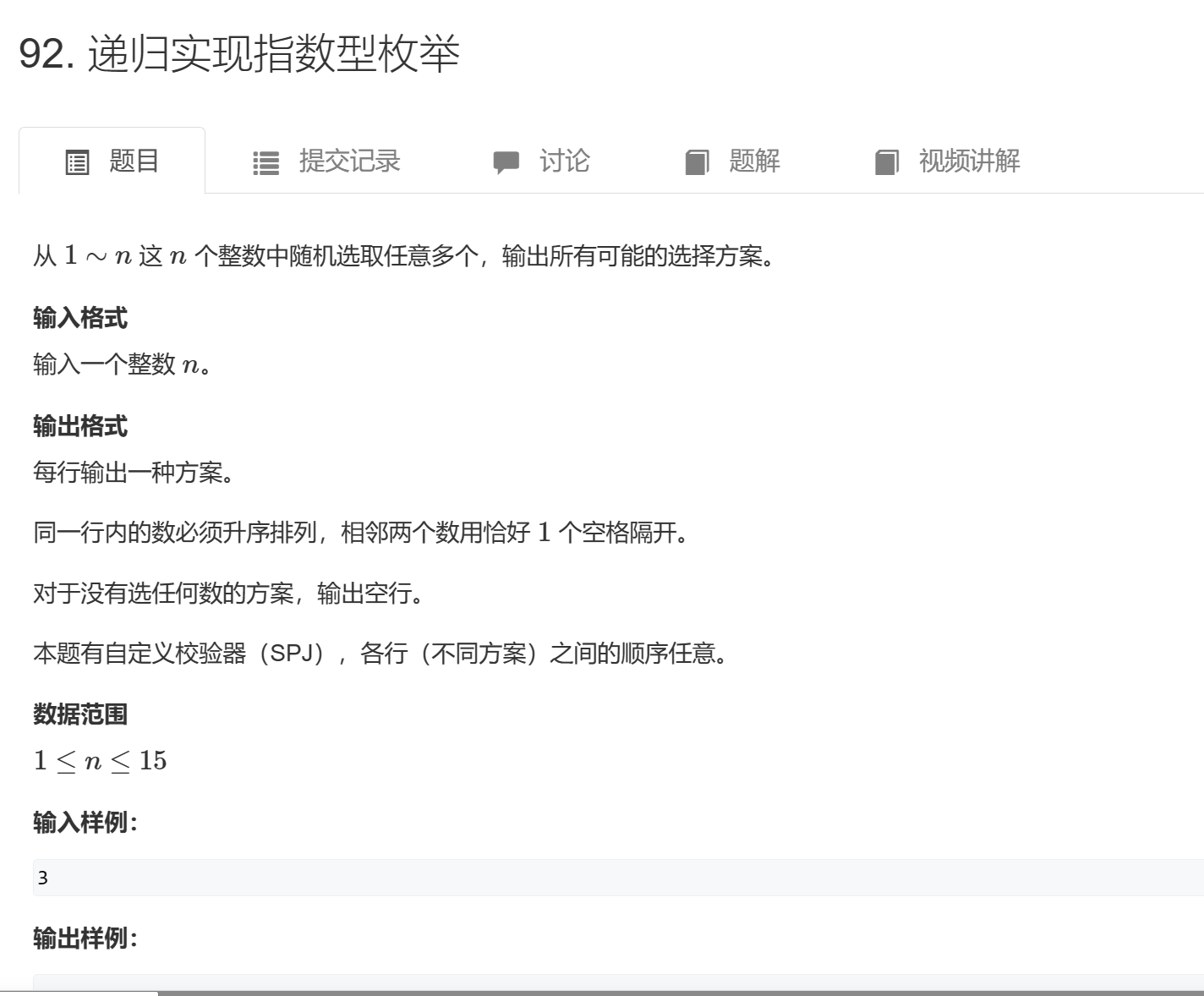
思路:
一、先去确定状态:
阶段就是深度,即选了几个数了
决策就是选与不选,没东西影响决策
开个全局数组记录答案即可
因此状态就是dfs(x)
二、枚举决策:选or不选
三、确定出口:深度>n
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
vector<int> v;
int n;
int vis[mxn];
void print(){for(int i=0;i<v.size();i++) cout<<v[i]<<" \n"[i==v.size()-1];
}
void dfs(int u){if(u>n){print();return;}v.push_back(u);dfs(u+1);v.pop_back();dfs(u+1);
}
void solve(){cin>>n;dfs(1);cout<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}AcWing 94. 递归实现排列型枚举 - AcWing

一、设状态:
阶段:深度,即选了几个数
影响决策的因素:只能选没选过的数:开个全局vis
记录答案:开个全局数组记录答案
二、枚举决策:
1~n,然后不选vis[i]=1的就行
三、出口:
深度>n
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
vector<int> v;
int n;
int vis[mxn];
void print(){for(int i=0;i<v.size();i++) cout<<v[i]<<" \n"[i==v.size()-1];
}
void dfs(int u){if(u>n){print();return;}for(int i=1;i<=n;i++){if(!vis[i]){v.push_back(i);vis[i]=1;dfs(u+1);vis[i]=0;v.pop_back();}}
}
void solve(){cin>>n;dfs(1);
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}93. 递归实现组合型枚举 - AcWing题库
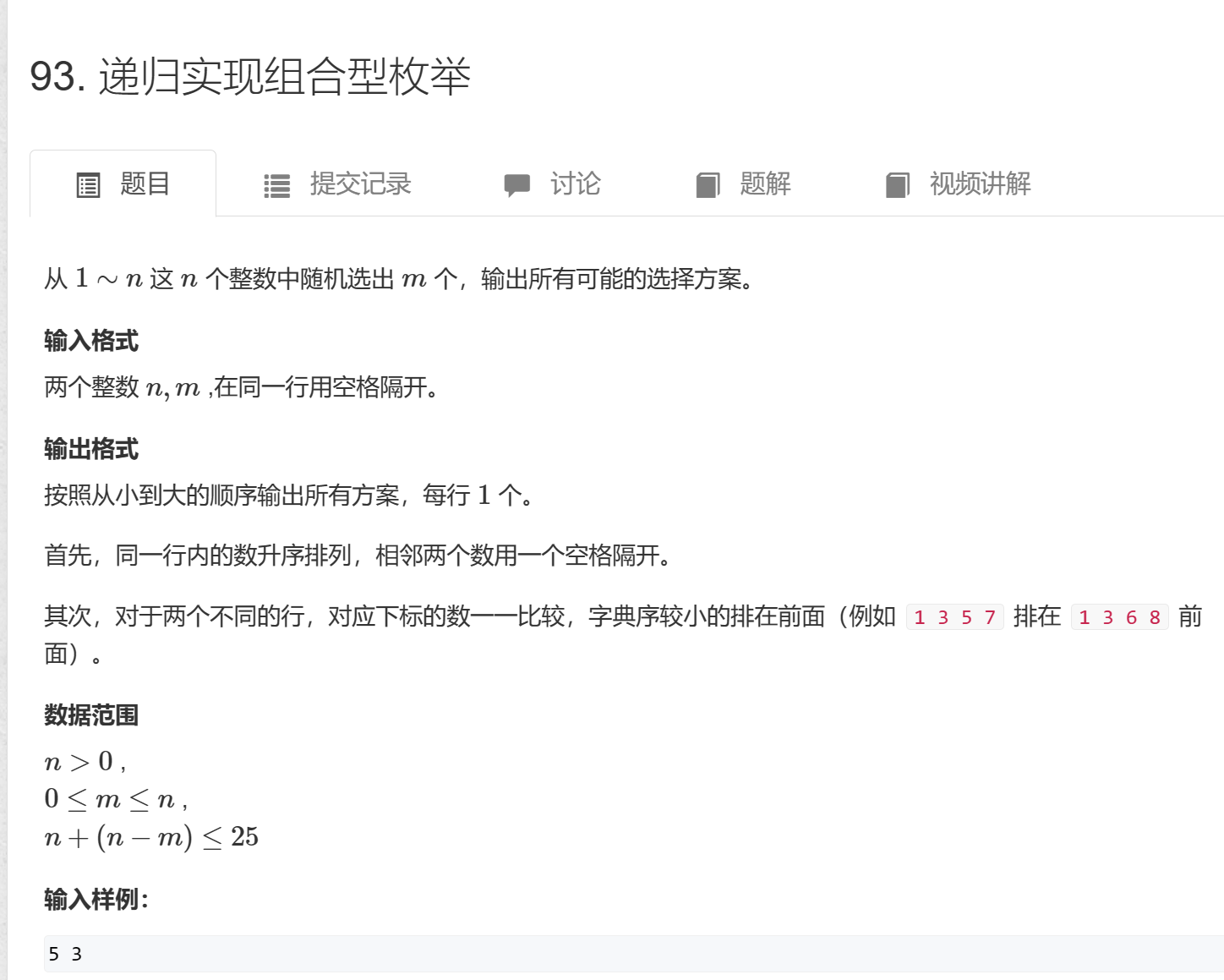
一、确定状态:
阶段:即深度,选不超过m个数
影响决策的因素:每次选比上次选的数大的,因此要记录上次选的数
记录结果:开个全局数组就行了
因此状态就是dfs(u,last),第二维是上次选的数
二、枚举决策:
从last+1开始枚举即可,不用开vis数组,不会重复
三、出口:
选了>m个数
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;int n,m,len=0;
int vis[mxn],a[mxn];
void print(){for(int i=1;i<=len;i++) cout<<a[i]<<" \n"[i==len];
}
void dfs(int u,int last){if(u>m){print();return;}for(int i=last+1;i<=n;i++){if(!vis[i]){vis[i]=1;a[++len]=i;dfs(u+1,i);len--;vis[i]=0;}}
}
void solve(){cin>>n>>m;dfs(1,0);
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}AcWing 1209. 带分数 - AcWing
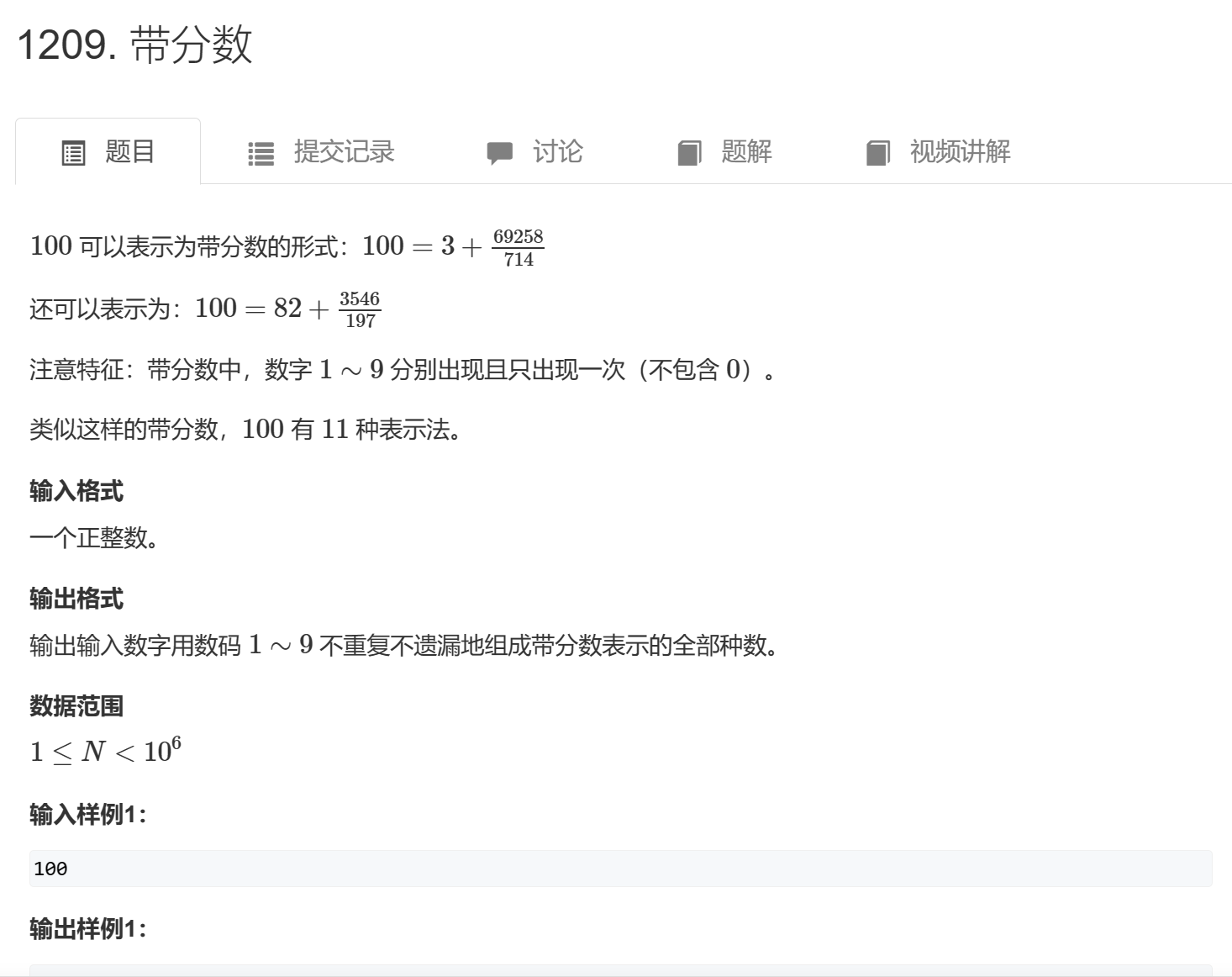
枚举对象:先去枚举全排列,然后枚举两个指针隔起来,验证正确性就好了,不需要dfs爆搜
有个细节就是:不要用substr,写个函数更清晰
Code:
#include <bits/stdc++.h>
//#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;int n;
string s="123456789";
bool check(int x1,int x2,int x3){if(x2%x3==0&&x1+x2/x3==n) return true;return false;
}
int trans(int l,int r){int res=0;for(int i=l;i<=r;i++){res=res*10+(s[i]-'0');}return res;
}
void solve(){int ans=0;cin>>n;do{for(int i=0;i<9;i++){for(int j=i+1;j<9;j++){int a1=trans(0,i);int a2=trans(i+1,j);int a3=trans(j+1,8);if(a1==0||a2==0||a3==0) continue;if(check(a1,a2,a3)) ans++;}}}while(next_permutation(s.begin(),s.end()));cout<<ans<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}AcWing 1208. 翻硬币 - AcWing
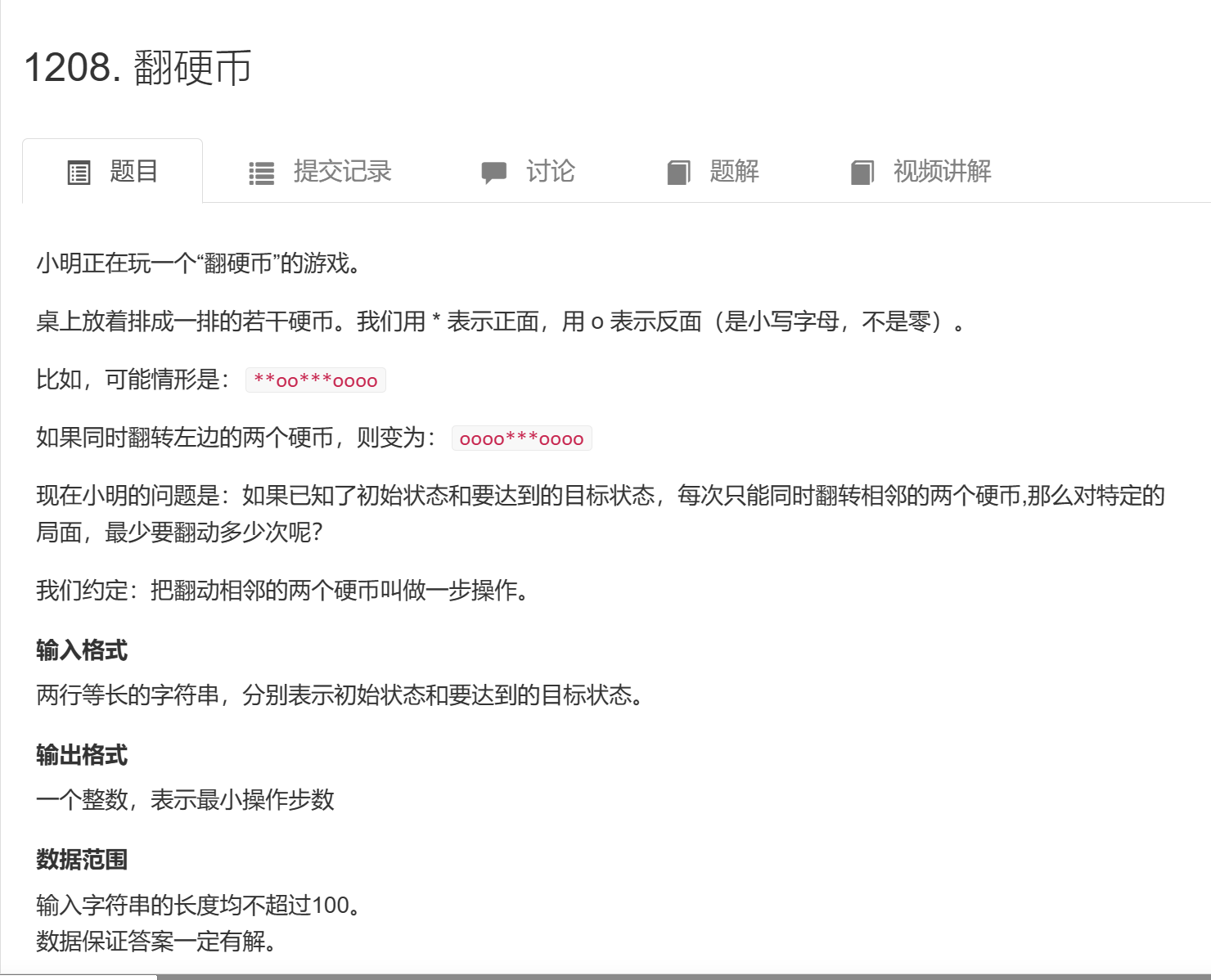
思路:
这是典中典,第一个是确定的,因此只需递推过去就好了
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;string s,t;
void solve(){cin>>s>>t;int cnt=0;for(int i=0;i<s.size();i++){if(s[i]!=t[i]){cnt++;if(s[i]=='*') s[i]='o';else s[i]='*';if(s[i+1]=='o') s[i+1]='*';else s[i+1]='o';}}cout<<cnt<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}相关文章:

Acwing 蓝桥杯 第一章 递归与递推
我上周在干什么,感觉我上周啥也没训,本来两天一次的vp也没v很寄啊,再这样下去真不行了先总结一下如何爆搜:先去确定好枚举的对象枚举的对象很重要!!这直接影响了复杂度然后就是去想递归树就好了一、确定状态…...

模型部署笔记
目录模型部署工作ONNX存在的意义ONNX(Open Neural Network Exchange)ONNX示例模型推理示例Batch调整量化量化方式常见问题模型部署工作 训练好的模型在特定软硬件平台下推理针对硬件优化和加速的推理代码 训练设备平台: CPU、GPU、DSP ONN…...
多线程之wait和notify
目录 1.wait()方法 2. notify方法 因为线程之间是抢占式执行的,所以线程之间执行的先后顺序难以预知。但是实际开发中,我们希望线程之间的执行顺序是能被掌控的,比如线程2开始之前,需要线程1的某个任务先被执行。也就是说,很多时…...
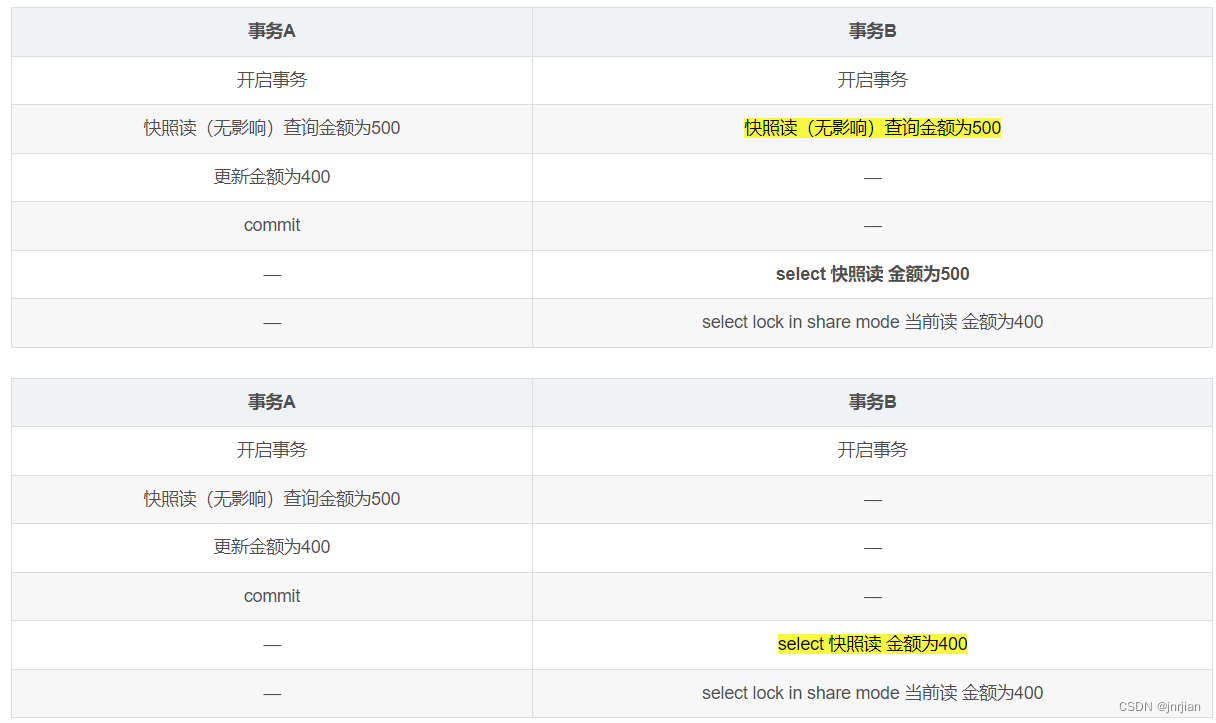
MVCC 当前读 快照读 RC read view RR下事务更新不会丢失
MVCC(multi-version-concurrent-control) MVCC是行锁的一个变种,但MVCC在很多情况下它避免了加锁。不是buffer块,而是buffer中的记录行。 MVCC (Multi-Version Concurrency Control) (注:与MVCC相对的,是基于锁的并发控制&#x…...

NCRE计算机等级考试Python真题(二)
第二套试题1、关于算法的描述,以下选项中错误的是A.算法具有可行性、确定性、有穷性的基本特征B.算法的复杂度主要包括时间复杂度和数据复杂度C.算法的基本要素包括数据对象的运算和操作及算法的控制结构D.算法是指解题方案的准确而完整的描述正确答案: …...

借助IBM Spectrum LSF为芯片行业大幅提升算力,预测未来
IBM Spectrum LSF 客户案例——上海开赟软件服务有限公司借助IBM Spectrum LSF为芯片行业大幅提升算力,预测未来 业务影响 中国芯片市场作为全球消费芯片市场重要组成部分,近年来发展迅猛。据国家统计局统计,2019年中国集成电路产量突破200…...

力扣-换座位
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:626. 换座位二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结前言 …...

DFT基本入门介绍
1.什么是DFT?2.为什么要做DFT?3.“测试”与“验证”的区别4.DFT的核心技术1)扫描路径设计(Scan Design)2)内建自测试(Bist)3)JTAG4)ATPG5.DFT工程师的岗位职责随着芯片的制程越来小(5nm), 芯片的规模越来越…...
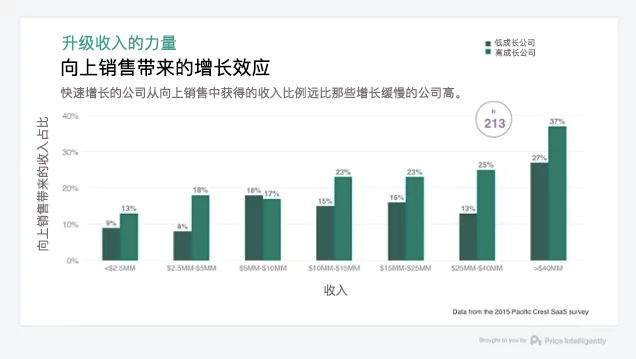
做「增长」必须懂的6大关键指标
无论你所从事的是哪个行业,增长都不是一件易事,SaaS公司想要维持长期的增长更是难上加难。这是因为SaaS公司对未来回报的依赖程度更大,反观那些传统商业模式的公司,主要的收入来源都集中在产品购买交付的时点上,而客户…...

Linux:soft lockup 检测机制
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 分析背景 本文分析基于 linux-4.14.132 内核代码分析,运行环境 Ubuntu 16.04.4 LTS QEMU ARM vexpress-a9 ,rootfs 基…...

天线理论知识4——非频变天线
目录 简介自补结构巴比涅原理天线的描述常见的非频变天线简介 所谓的非频变天线指的是天线的参数几乎不随着频率的改变而发生变化。 自补结构 天线的自补结构指的是:由无限大且无厚度的理想导电区域的自由空间中的非导电区域放置一起的结构称为自补结构。包含金属部分和非金…...

基础架构组件选型及服务化
常见的分布式基础架构组件 分布式服务化框架,业界开源产品比如 Dubbo、Spring Cloud 这样的框架;分布式缓存及框架,业界如 Redis、Memcached,框架如 Codis 和 Redis Cluster;数据库及分布式数据库框架,这两…...
leetcode-每日一题-1247(中等,数学逻辑)
这道题当理解清了意思之后,只要是s1和s2的某位置的字母一样时我们就可以忽视比如s1"xxxxxxyyyy"; 就可以看成s1"xxxyyyy";s2"xxxyyyxxxx"; s2"yyyxxxx";其次就是只有当x和y位置差异产生的数量同奇偶的时候才可以构成相等字…...
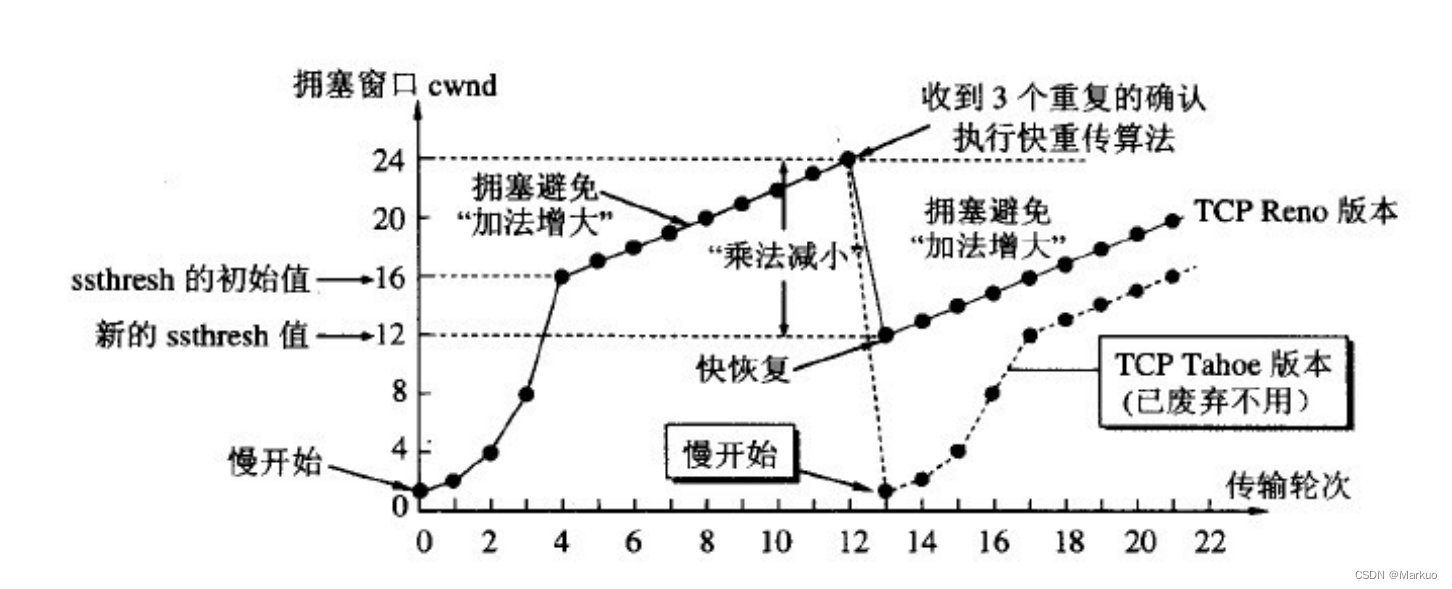
前端面试题 —— 计算机网络(一)
目录 一、常见的HTTP请求头和响应头 二、HTTP状态码304是多好还是少好? 三、OPTIONS请求方法及使用场景 四、对keep-alive的理解 五、HTTP协议的优点和缺点 六、URL有哪些组成部分? 七、HTTPS通信(握手)过程 八、HTTPS的特…...
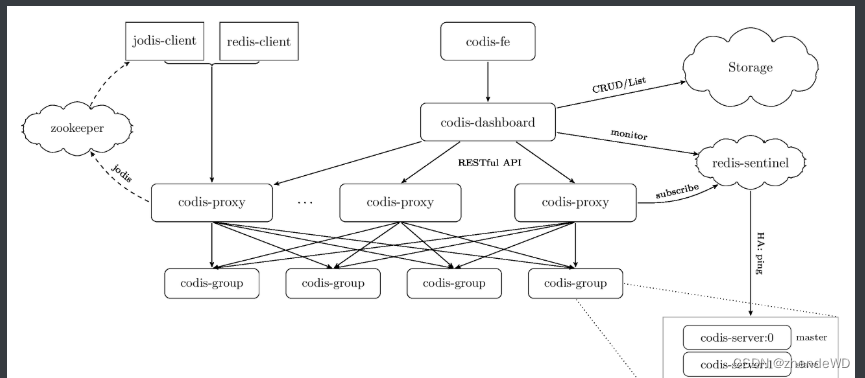
分布式-分布式缓存笔记
分布式系统缓存 缓存分类 前端缓存 前端缓存包括页面和浏览器缓存,如果是 App,那么在 App 端也会有缓存。当你打开商品详情页,除了首次打开以外,后面重复刷新时,页面上加载的信息来自多种缓存。 页面缓存属于客户端…...

【反序列化漏洞-01】为什么要序列化
为什么要序列化百度百科上关于序列化的定义是,将对象的状态信息转换为可以存储或传输的形式(字符串)的过程。在序列化期间,对象将其当前状态写入到临时或持久性存储区(非关系型键值对形式的数据库Redis,与数组类似)。以后,可以通过…...

用c语言模拟实现常用字符串函数
目录 一.常用字符串函数介绍 1.strlen 2. strcpy 3.strcmp 4.strcat 5.strstr 二.模拟实现常用字符串函数 1.strlen 2.strcpy 3.strcmp 4.strcat 5.strstr 一.常用字符串函数介绍 1.strlen 字符串strlen是用来求字符串长度的,我们可以打开cpp网站查看有关…...
在 Flutter 中使用 webview_flutter 4.0 | 基础用法与事件处理
大家好,我是 17。 Flutter WebView 一共写了四篇文章 在 Flutter 中使用 webview_flutter 4.0 | 基础用法与事件处理在 Flutter 中使用 webview_flutter 4.0 | js 交互Flutter WebView 性能优化,让 h5 像原生页面一样优秀,已入选 掘金一周 …...
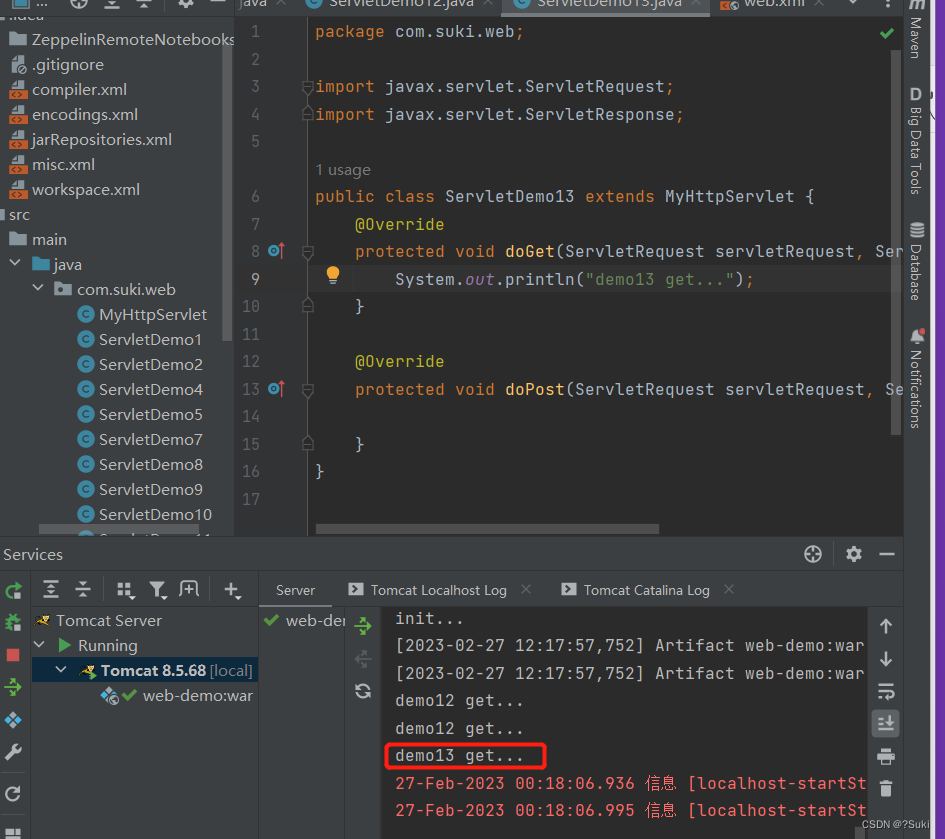
JavaWeb--Servlet
Servlet1 简介2 快速入门3 执行流程4 生命周期5 方法介绍6 体系结构7 urlPattern配置8 XML配置目标: 理解Servlet的执行流程和生命周期掌握Servlet的使用和相关配置 1 简介 Servlet是JavaWeb最为核心的内容,它是Java提供的一门动态web资源开发技术。 使…...
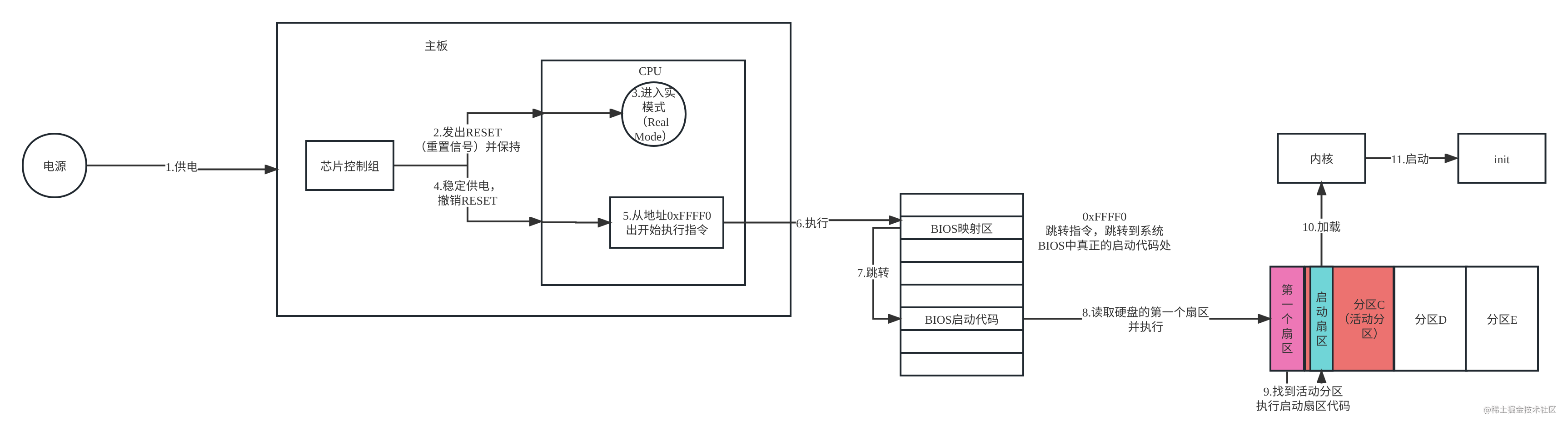
Linux启动过程
theme: channing-cyan 两种启动方式 传统启动方式(LEGACYMBR) 指传统BIOS启动方式,存在一些不足:比如最大只支持2TB磁盘,磁盘最多四个分区,且不支持图形操作 UEFIGPT方式 是新式的启动方式,…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
