数据结构与算法(五):优先队列
这节总结一下优先队列的常用实现方法。
一、基本概念
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (largest-in,first-out)的行为特征。
抽象数据类型:
优先队列的接口同前面讲到的队列的接口一样,是其基于泛型的API接口代码如下:
public interface Queue<E> {//队列是否为空boolean isEmpty();//队列的大小int size();//入队void enQueue(E element);//出队E deQueue();
}
二、基于数组实现的优先队列
实现优先队列最简的方法就是基于前面讲到的基于数组的栈的代码,只需对插入或删除操作作相应的更改即可。
1、基于有序数组的实现
在栈的代码的插入方法中添加代码,将所有较大的元素向右移动一格,以保证数组有序(和插入排序相同),这里我们可以使用二分查找的方法来找出元素应插入的位置,然后再移动元素。这样最大元素,总是在数组的最右边,其删除操作和栈的实现中一样。
代码:
/*** 基于有序数组的实现的优先队列* @author Alent* @param <E>*/
public class PriorityQueue<E extends Comparable<E>> implements Queue<E>{private E[] elements;private int size=0;@SuppressWarnings("unchecked")public PriorityQueue() {elements = (E[])new Comparable[1]; }@Override public int size() {return size;}@Override public boolean isEmpty() {return size == 0;}@Overridepublic void enQueue(E element) {if(size == elements.length) {resizingArray(2*size);//若数组已满将长度加倍}elements[size++] = element;insertSort(elements);}@Overridepublic E deQueue() {E element = elements[--size];elements[size] = null; //注意:避免对象游离if(size > 0 && size == elements.length/4) {resizingArray(elements.length/2);//小于数组1/4,将数组减半}return element;}//插入排序,由于前面n-1个元素是有序的,这里只插入最后一个元素public void insertSort(E[] a) {int N = size -1; //最后一个元素是size-1,不是a.length-1if(N == 0) return;int num = binaryFind(a, a[N], 0, N-1);E temp = a[N];//num后的元素向后移动for (int j = N; j > num; j--) {a[j] = a[j-1];}a[num] = temp;}//找出元素应在数组中插入的位置public int binaryFind(E[] a, E temp, int down, int up) {if(up<down || up>a.length || down<0) {System.out.println("下标错误");}if(temp.compareTo(a[down]) < 0) return down;if(temp.compareTo(a[up]) > 0) return up+1;int mid = (up-down)/2 + down;if(temp.compareTo(a[mid]) == 0) {return mid + 1;}else if(temp.compareTo(a[mid])<0) {up = mid-1;}else if(temp.compareTo(a[mid])>0) {down = mid+1;}return binaryFind(a,temp,down,up);}//交换两个元素public void swap(E[] a,int i,int j) {E temp = a[i];a[i] = a[j];a[j] = temp;}//调整数组大小public void resizingArray(int num) {@SuppressWarnings("unchecked")E[] temp = (E[])new Comparable[num];for(int i=0;i<size;i++) {temp[i] = elements[i];}elements = temp;}public static void main(String[] args) {int[] a = {4,2,1,3,8,new Integer(5),7,6};//测试数组PriorityQueue<Integer> pq = new PriorityQueue<Integer>();System.out.print("入栈顺序:");for(int i=0;i<a.length;i++) {System.out.print(a[i]+" ");pq.enQueue(a[i]);}System.out.println();System.out.print("出栈顺序数组实现:");while(!pq.isEmpty()) {System.out.println(pq.deQueue());}}
}
2、基于无序数组的实现
同样,我们一个可以在删除方法中修改,在删除方法中添加一段类似于选择排序内循环的代码,每次删除时先找出数组中的最大元素,然后与最右边元素进行交换,然后在删除元素。
代码:
@Override
public void enQueue(E element) {if(size == elements.length) {resizingArray(2*size);//若数组已满将长度加倍}elements[size++] = element;
}@Override
public E deQueue() {swapMax(elements);E element = elements[--size];elements[size] = null; //注意:避免对象游离if(size > 0 && size == elements.length/4) {resizingArray(elements.length/2);//小于数组1/4,将数组减半}return element;
}public void swapMax(E[] a) {int max = size -1;for(int i=0;i<size-1; i++) {if(larger(a[i],a[max])) max = i;}swap(a, size-1, max);
}//比较两个元素大小
public boolean larger(E a1, E a2) {return a1.compareTo(a2)>0;
}
三、基于堆实现的优先队列
基本概念:
当一个二叉树的每个结点都大于等于它的两个子结点时,我们称它是堆有序的。根结点是堆有序的二叉树的最大结点。
二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级存储。
一棵堆有序的完全二叉树
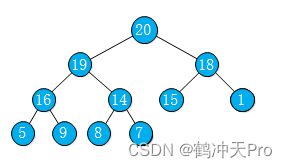
为了操作方便,这是我们使用一个数组,来表示一个堆。我们不使用数组的第一个元素,具体实现在《数据结构与算法(四),树》中有提及,这里就不说了。
1、堆的有序化
当我们将元素插入到堆(数组的末尾)中时,插入的元素可能比它的父结点要大,堆的有序状态被打破。我们需要交换它和它的父节点来修堆,直到堆重新变为有序状态。其操作如下图:
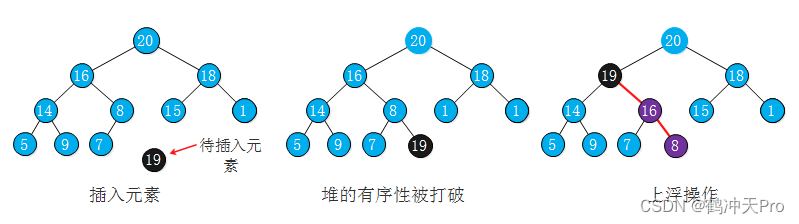
代码如下:
//上浮操作
private void swim(int k) {while(k > 1 && less(k/2, k)) {swap(k/2, k);k = k/2;}}private boolean less(int i, int j) {return elements[i].compareTo(elements[j]) < 0;
}//交换两个元素
public void swap(int i,int j) {E temp = elements[i];elements[i] = elements[j];elements[j] = temp;
}
同样的,当我们从堆中删除根结点并将它的最后一个元素放到顶端时,堆的有序性被打破,我们需要将它与它的两个子结点种的较大者进行交换,以恢复堆的有序性,其操作流程如下图:
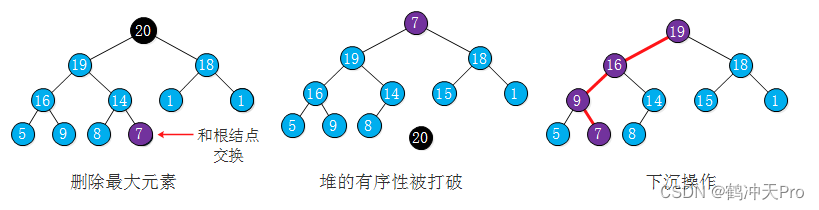
其代码如下:
//下沉操作
private void sink(int k) {while(2*k <= size) {int j = 2*k;if(j < size && less(j, j+1))j++;if(!less(k,j))break;swap(k,j);k = j;}
}
2、基于堆实现的优先队列
基于堆的优先队列的实现代码如下:
/*** 基于堆的优先队列* @author Alent*/
public class MaxPQ<E extends Comparable<E>> implements Queue<E>{private E[] elements;private int size=0;@SuppressWarnings("unchecked")public MaxPQ(int capacity) {elements = (E[])new Comparable[capacity + 1]; }@Override public int size() {return size;}@Override public boolean isEmpty() {return size == 0;}@Overridepublic void enQueue(E element) {elements[++size] = element;swim(size);}//上浮private void swim(int k) {while(k > 1 && less(k/2, k)) {swap(k/2, k);k = k/2;}}private boolean less(int i, int j) {return elements[i].compareTo(elements[j]) < 0;}@Overridepublic E deQueue() {E result = elements[1];swap(1, size--);elements[size + 1] = null;sink(1);return result;}//下沉private void sink(int k) {while(2*k <= size) {int j = 2*k;if(j < size && less(j, j+1))j++;if(!less(k,j))break;swap(k,j);k = j;}}//交换两个元素public void swap(int i,int j) {E temp = elements[i];elements[i] = elements[j];elements[j] = temp;}
}
三种实现方法的时间复杂度比较:
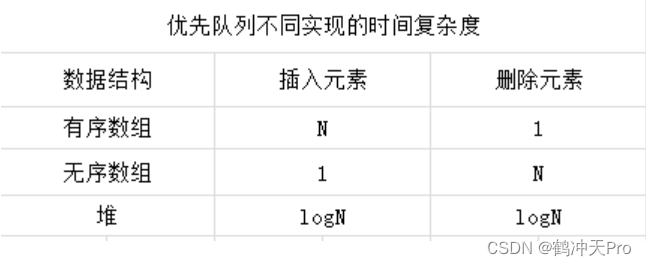
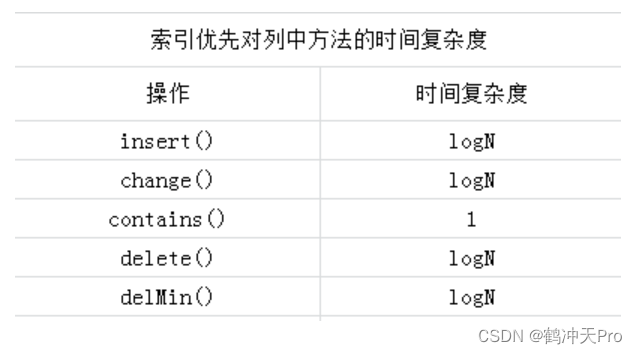
四、索引优先队列
索引优先队列,它用一个索引数组保存了某个元素在优先队列中的位置,使得我们能够引用已经进入优先队列中的元素。最在些应用中,通常是很有必要的,如:有向图的Dijkstra算法中就使用了索引优先队列,来返回最小边的索引。
其实现方法为:
使用elements[]数组来保存队列中的元素,pq[]数组用来保存elements中元素的索引,在添加一个数组qp[]来保存pq[]的逆序——qp[i]的值是i在pq[]中的位置(即 pq[qp[i]] = i)。若i不在队列中,则令qp[i] = -1。辅助函数less()、swap()、sink()、swim()和前面优先队列中的一样。
索引优先队列的代码实现:
/*** 基于堆实现的索引优先队列*/
public class IndexMinPQ<E extends Comparable<E>>{private int[] pq; //索引二叉堆private int[] qp; // 保存逆序:pq[qp[i]] = i;private E[] elements; //元素private int size = 0;@SuppressWarnings("unchecked")public IndexMinPQ(int capacity) {elements = (E[]) new Comparable[capacity + 1];pq = new int[capacity + 1];qp = new int[capacity + 1];for (int i = 0; i <= capacity; i++) {qp[i] = -1;}}public boolean isEmpty() {return size == 0;}//删除最小元素,并返回索引public int delMin() {int index = pq[1];swap(1, size--);sink(1);elements[pq[size + 1]] = null;qp[pq[size + 1]] = -1;return index;}//删除索引k及其元素public void delete(int k) {int index = qp[k];swap(index, size--);swim(index);sink(index);elements[k] = null;qp[k] = -1;}//插入元素,将它和索引k关联public void insert(int k, E element) {size++;qp[k] = size;pq[size] = k;elements[k] = element;swim(size);}//改变索引k关联的元素public void change(int k, E element) {elements[k] = element;swim(qp[k]);sink(qp[k]);}//是否包含索引kpublic boolean contains(int k) {return qp[k] != -1;}//下沉private void sink(int k) {while (2 * k <= size) {int j = 2 * k;if (j < size && less(j, j + 1))j++;if (!less(k, j))break;swap(k, j);k = j;}}//上浮private void swim(int k) {while (k > 1 && less(k / 2, k)) {swap(k, k / 2);k = k / 2;}}private boolean less(int i, int j) {return elements[pq[i]].compareTo(elements[pq[j]]) > 0;}//交换两元素private void swap(int i, int j) {int swap = pq[i];pq[i] = pq[j];pq[j] = swap;qp[pq[i]] = i;qp[pq[j]] = j;}
}
索引优先队列的时间复杂度:
相关文章:

数据结构与算法(五):优先队列
这节总结一下优先队列的常用实现方法。 一、基本概念 普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级…...
二叉树的前序遍历-java两种方式-力扣144
一、题目描述给你二叉树的根节点 root ,返回它节点值的 前序 遍历。示例 1:输入:root [1,null,2,3]输出:[1,2,3]示例 2:输入:root []输出:[]示例 3:输入:root [1]输出…...
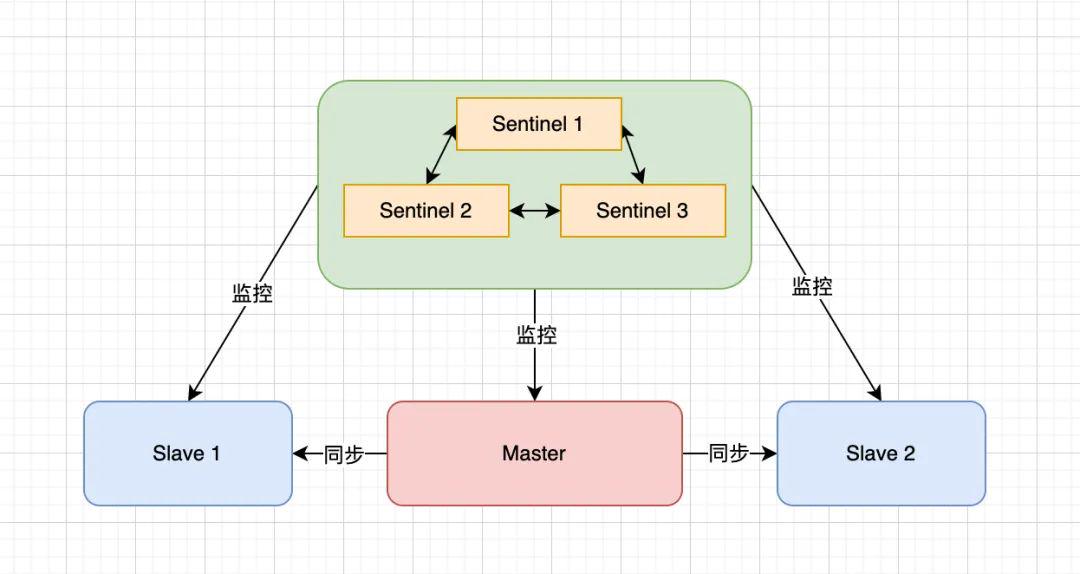
浅析 Redis 主从同步与故障转移原理
我们在生产中使用 Redis,如果只部署一个 Redis 实例,当该实例宕机,到恢复之前都不可用;虽说 Redis 一般都用来做缓存,但不可用给业务系统带来的影响也是不小的,流量大时甚至会导致整个服务宕机。所以 Redis…...
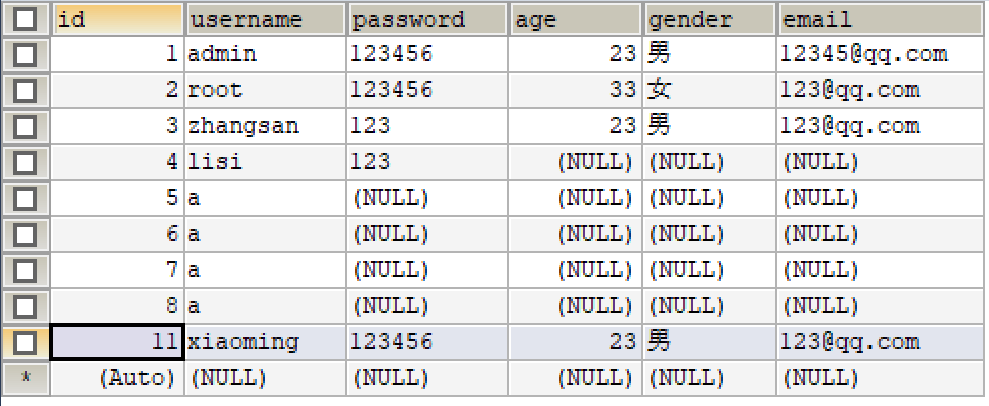
MyBatis学习笔记(七) —— 特殊SQL的执行
7、特殊SQL的执行 7.1、模糊查询 模糊查询的三种方式: 方式1:select * from t_user where username like ‘%${mohu}%’ 方式2:select * from t_user where username like concat(‘%’,#{mohu},‘%’) 方式3:select * from t_u…...
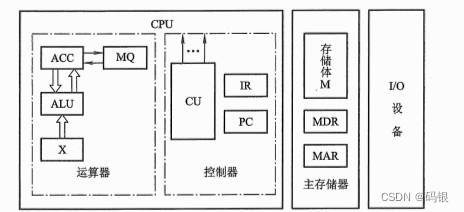
计算机组成原理(1)--计算机系统概论
一、计算机系统简介1.计算机系统软硬件概念计算机系统由“硬件”和“软件”两大部分组成。所谓“硬件”,是指计算机的实体部分,它由看得见摸得着的各种电子元器件,各类光、电、机设备的实物组成,如主机、外部设备等。所谓“软件”…...
jdbc模板的基本使用
1.JdbcTemplate的开发步骤 <1>导入spring-jdbc和spring-tx坐标 <2>创建数据库表和实体 <3>创建JdbcTemplate对象 <4>执行数据库 2.JdbcTemplate快速入门 <1>导入坐标 <dependency><groupId>org.springframework</groupId><…...

JPA 注解及主键生成策略使用指南
JPA 注解 Entity 常用注解 参考:JPA & Spring Data JPA学习与使用小记 指定对象与数据库字段映射时注解的位置:如Id、Column等注解指定Entity的字段与数据库字段对应关系时,注解的位置可以在Field(属性)或Prope…...
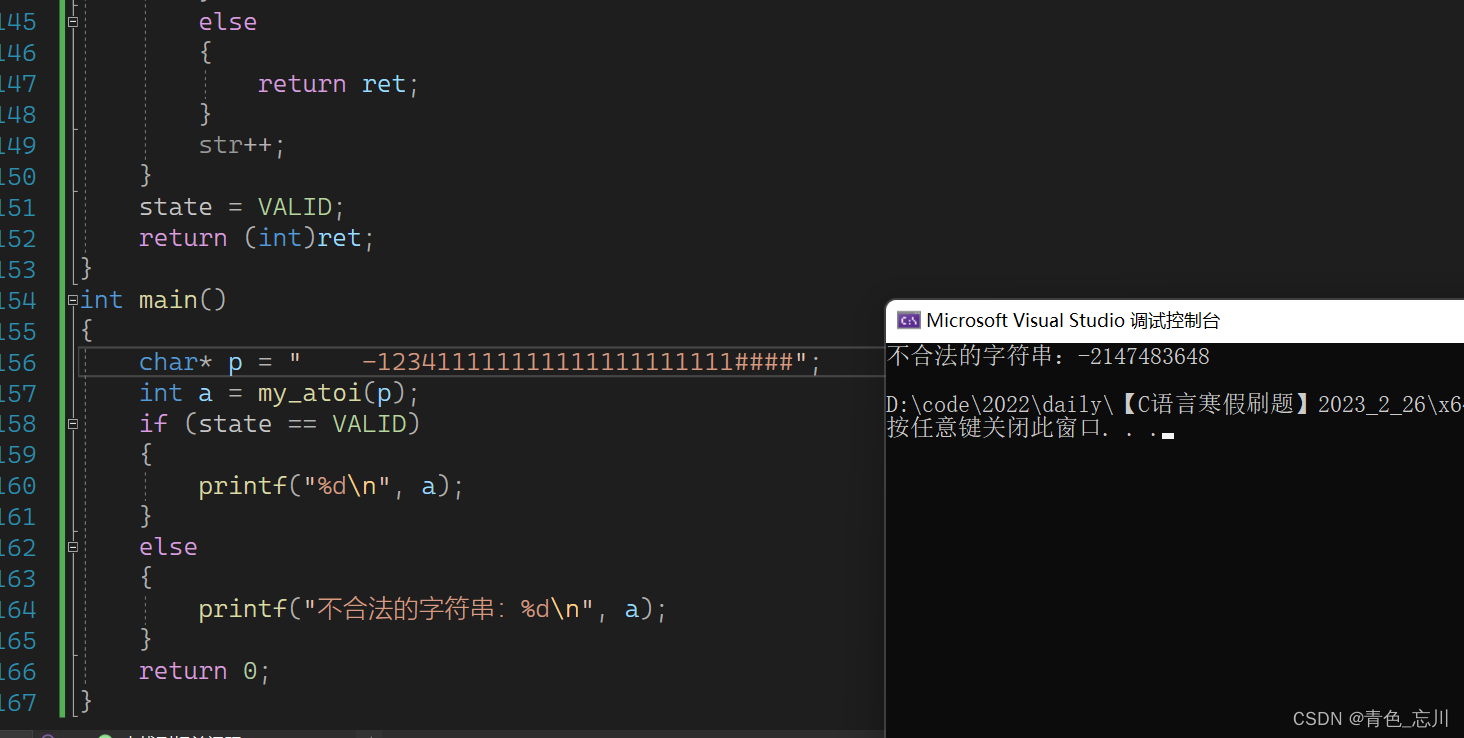
【C语言刷题】找单身狗、模拟实现atoi
目录 一、找单身狗 1.暴力循环法 2.分组异或法 二、模拟实现atoi 1.atoi函数的功能 2.模拟实现atoi 一、找单身狗 题目描述:给定一个数组中只有两个数字是出现一次,其他所有数字都出现了两次。 编写一个函数找出这两个只出现一次的数字。 比如&…...

前端必会面试题指南
计算属性和watch有什么区别?以及它们的运用场景? // 区别computed 计算属性:依赖其它属性值,并且computed的值有缓存,只有它依赖的属性值发生改变,下一次获取computed的值时才会重新计算computed的值。watch 侦听器:…...

C 语言—— 数组
【C 语言】数组1. 概念2. 声明3. 分类4. 初始化5. 赋值6. 附加语法7. VLA 的一些补充1. 概念 数组是存放一组 相同类型 的 有序 数据的一段 连续 空间。 2. 声明 TYPE identifier[static(optional) qualifiers(optional) expression(optional)] TYPE identifier[qualifiers(o…...
Oracle-RAC集群主机重启问题分析
问题背景: 在对一套两节点Oracle RAC19.18集群进行部署时,出现启动数据库实例就会出现主机出现重启的情况,检查发现主机重启是由于节点集群被驱逐导致。 问题: 两节点Oracle RAC19.18集群,启动数据库实例会导致主机出现重启。 问题分析: 主机多次出现…...
Python每日一练(20230227)
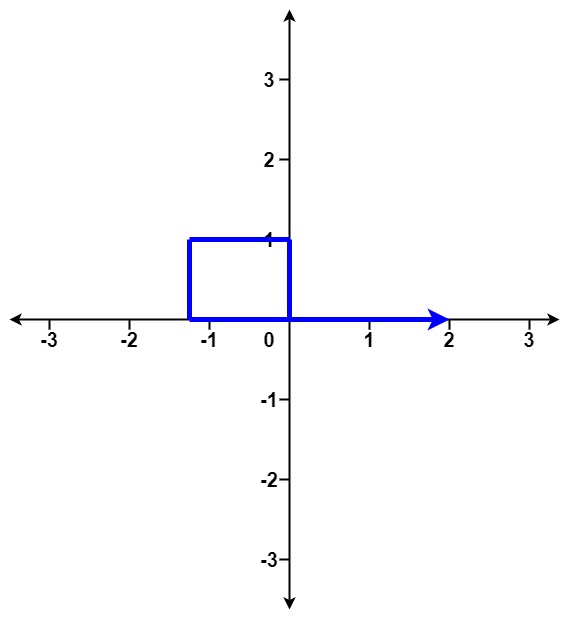
目录 1. 路径交叉 ★★★ 2. 缺失的第一个正数 ★★★ 3. 寻找两个正序数组的中位数 ★★★ 附录 散列表 基本概念 常用方法 1. 路径交叉 给你一个整数数组 distance 。 从 X-Y 平面上的点 (0,0) 开始,先向北移动 distance[0] 米,然后向西移…...

Scratch少儿编程案例-算法练习-存款收益计算
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...

【Linux驱动开发100问】Linux驱动开发工程师在面试中常被问到的问题汇总
🥇今日学习目标:什么是Kconfig?如何使用Kconfig? 🤵♂️ 创作者:JamesBin ⏰预计时间:10分钟 🎉个人主页:嵌入式悦翔园个人主页 🍁专栏介绍:Lin…...

每日学术速递2.27
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CL 1.FiTs: Fine-grained Two-stage Training for Knowledge-aware Question Answering 标题:FiTs:用于知识感知问答的细粒度两阶段训练 作者:Qichen…...

【数据库系统概论】基础知识总结
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
)
简单移动平均在量化中的应用(附Python实战代码)
在大多数金融产品的投资过程中,均线系统都是很重要的投资参考。一般来说,均线可以近似理解为某段时间内成交筹码的均价,它往往能帮助我们找到合适的支撑位和压力位。随着各种技术流派以及统计学的发展,从简单移动平均中逐渐衍生出了更多的均线计算方式,比如指数移动平均、…...
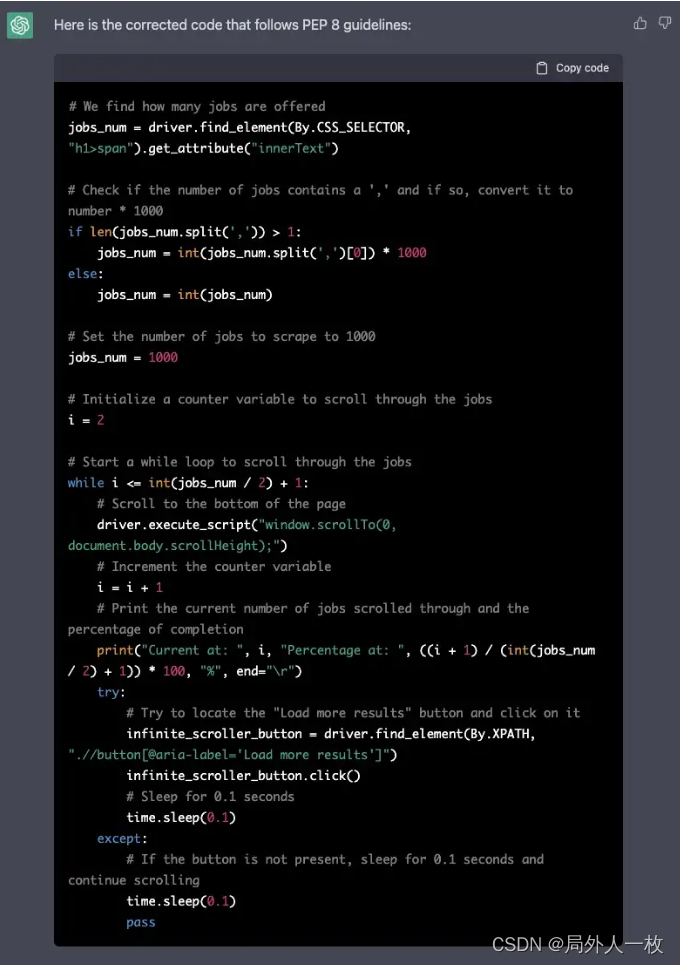
ChatGPT提高你日常工作的五个特点,以及如何使用它来提高代码质量
ChatGPT已经完全改变了代码开发模式。然而,大多数软件开发者和数据专家们仍然不使用ChatGPT来完善——并简化他们的工作。 这就是我们在这里列出提升日常工作效率和质量的5个不同的特点的原因。 让我们一起来看看在日常工作中如何使用他们。 警告:不要…...

spark datasourceV1和v2
datasourceV2 一文理解 Apache Spark DataSource V2 诞生背景及入门实战 https://zhuanlan.zhihu.com/p/83006243 2.3 Data source API v2 https://issues.apache.org/jira/browse/SPARK-15689 Because of the above limitations/issues, the built-in data source impleme…...
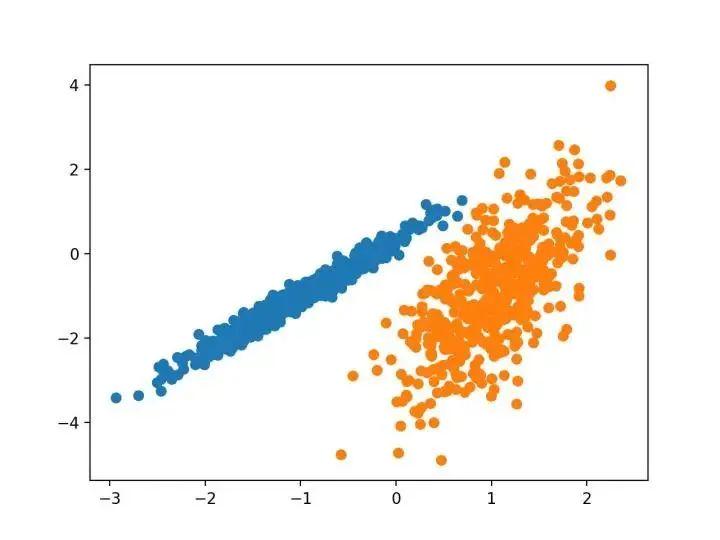
10种聚类算法的完整python操作示例
大家好,聚类或聚类分析是无监督学习问题。它通常被用作数据分析技术,用于发现数据中的有趣模式,例如基于其行为的客户群。有许多聚类算法可供选择,对于所有情况,没有单一的最佳聚类算法。相反,最好探索一系…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
