【代码随想录】算法训练营 第十五天 第六章 二叉树 Part 2
102. 二叉树的层序遍历
层序遍历,就是一层一层地遍历二叉树,最常见的就是从上到下,从左到右来遍历,遍历的方法依然有两种,第一种是借助队列,第二种则是递归,都算是很简单、很容易理解的方法,下面来分别介绍一下。
队列法
使用队列法讲究的就是一个简单粗暴,顺着做下去就行了。
首先要定义一个队列,这个队列的元素都得是二叉树结点,因为它是用来暂存二叉树的一层的。先是把根结点入队,当然如果连根结点都没有的话,就直接返回空数组了(要返回的是保存各层元素的二维数组,用vector容器实现);
接着就用vector定义一个保存遍历下来的元素的二维数组,作为result来最终返回答案;
现在就开始遍历了,我们用的是while循环,当队列为空时停止,在一轮循环中,队列存的是这层要遍历的结点,所以先定义一个size来保存未经遍历的层结点数,因为下面我们在遍历一个结点后就要把它出队,以便于存入下一层的结点;
遍历中,使用一个一维数组保存元素值,然后就把这个结点的左右子结点依次入队,因为是队列,就不用像栈那样反着来。每层遍历结束后,就把遍历得到的元素数组push进result二维数组里。
具体代码如下:
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;vector<vector<int>> result;if (root != NULL) que.push(root);while (!que.empty()) {int size = que.size();vector<int> vec;for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;}
};递归法
这个不用掌握,了解一下即可。但是下面的两道还是优先使用递归来做。
class Solution {
public:void order(TreeNode* cur, vector<vector<int>>& result, int depth) {if (cur == nullptr) return;if (result.size() == depth) result.push_back(vector<int>());result[depth].push_back(cur->val);order(cur->left, result,depth + 1);order(cur->right, result, depth + 1);}vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;int depth = 0;order(root, result, depth);return result;}
};226. 翻转二叉树
题目
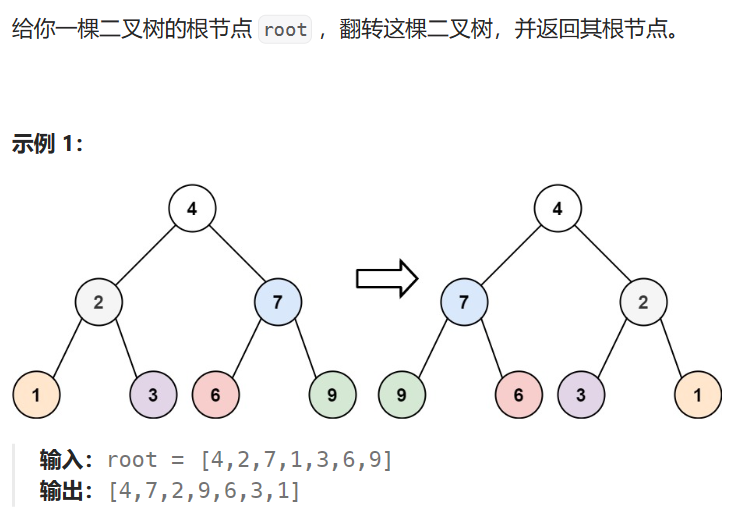
思路
看到翻转,你可能会先想到一层一层地将结点翻转,但其实不用这么复杂,稍微观察一下就知道,只需要翻转每个结点的两个子结点即可,所以这里就可以用递归遍历的方法来做,先对调两个子结点,再遍历子结点,最后返回根结点即可。
盲区
随想录刷到这里才知道,swap函数还可以用来对调两个二叉树结点,长知识了:
swap(root->left, root->right);代码
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right);invertTree(root->left);invertTree(root->right);return root;}
};101. 对称二叉树
题目
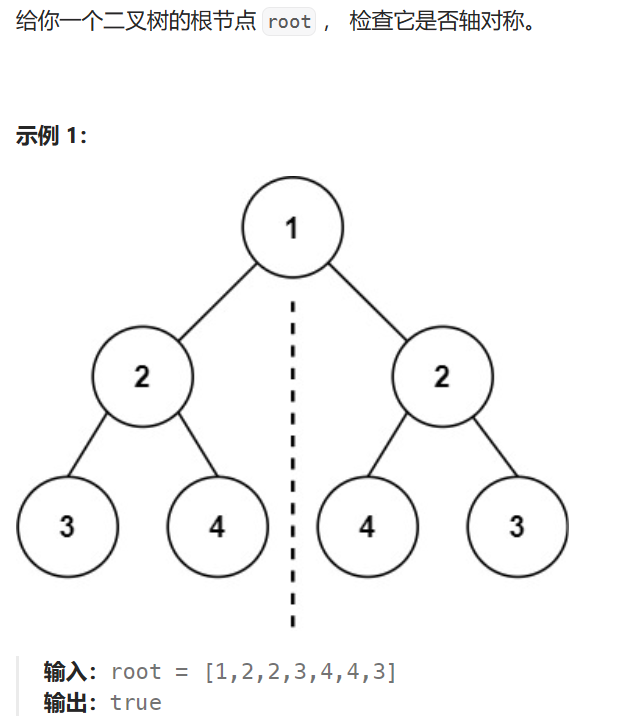
思路
还是用递归来做,每次递归判断对称的两个结点,若其中一个为空则返回false,两个都为空则返回true,接着都是不为空的,此时就判断两个结点值是否相等,不相等就返回false,否则就接着往下递归,先递归判断左边的左孩子和右边的右孩子,再递归判断左边的右孩子和右边的左孩子,这样就是对称位置的结点来判断是否相等了,将判断结果分别赋值给一个布尔变量,两个布尔变量都为true时就返回true。
代码
class Solution {
public:bool compare(TreeNode* left, TreeNode* right) {if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;else if (left->val != right->val) return false;bool outside = compare(left->left, right->right);bool inside = compare(left->right, right->left);bool isSame = outside && inside;return isSame;}bool isSymmetric(TreeNode* root) {if (root == NULL) return true;return compare(root->left, root->right);}
};相关文章:

【代码随想录】算法训练营 第十五天 第六章 二叉树 Part 2
102. 二叉树的层序遍历 层序遍历,就是一层一层地遍历二叉树,最常见的就是从上到下,从左到右来遍历,遍历的方法依然有两种,第一种是借助队列,第二种则是递归,都算是很简单、很容易理解的方法&am…...
使用ssl_certificate_by_lua指令动态加载证书
1、下载 OpenResty - 下载 根据自己系统选择下载,我的是64位 2、解压到目录 3、启动openresty 进入解压后的目录,执行nginx.exe 浏览器输入 http://localhost 查看是否正常。显示以下画面就表示没有问题。 接下来可以开始准备动态安装证书 4、使用o…...

Qt中Opencv转Qimage出现重影或者颜色不对
废话不多说 在qt中opencv获取的图像转qimage时出现重影原因: 图像数据的内存对齐可能会导致画面重影,如果出现误差转换出来的图就会出现重影 解决办法: cv::Mat image_bgr cv::imread(“example.jpg”); cv::Mat image_aligned; cv::copyMak…...
upload-labs-1
文章目录 Pass-01 Pass-01 先上传一个正常的图片,查看返回结果,结果中带有文件上传路径,可以进行利用: 上传一个恶意的webshell,里面写入一句话木马: <?php eval($_POST[cmd]); echo "hello&quo…...

【vite配置路径别名@】/启动配置
npm install types/node --save-dev npm install path --save import { defineConfig } from vite import vue from vitejs/plugin-vue // 配置别名 import { resolve } from "path";// https://vitejs.dev/config/ export default defineConfig({plugins: [vue()]…...

3. List
数据结构在Java集合中的对应关系 线性表【数组】 -> ArrayList 线性表【链表】-> LinkedList 队列 -> Queue -> LinkedList,PriorityQueue, ArrayBlockingQueue … etc. 双端队列 -> Deque -> ArrayDeque 栈 -> LinkedList 哈希表 -> Hash…...
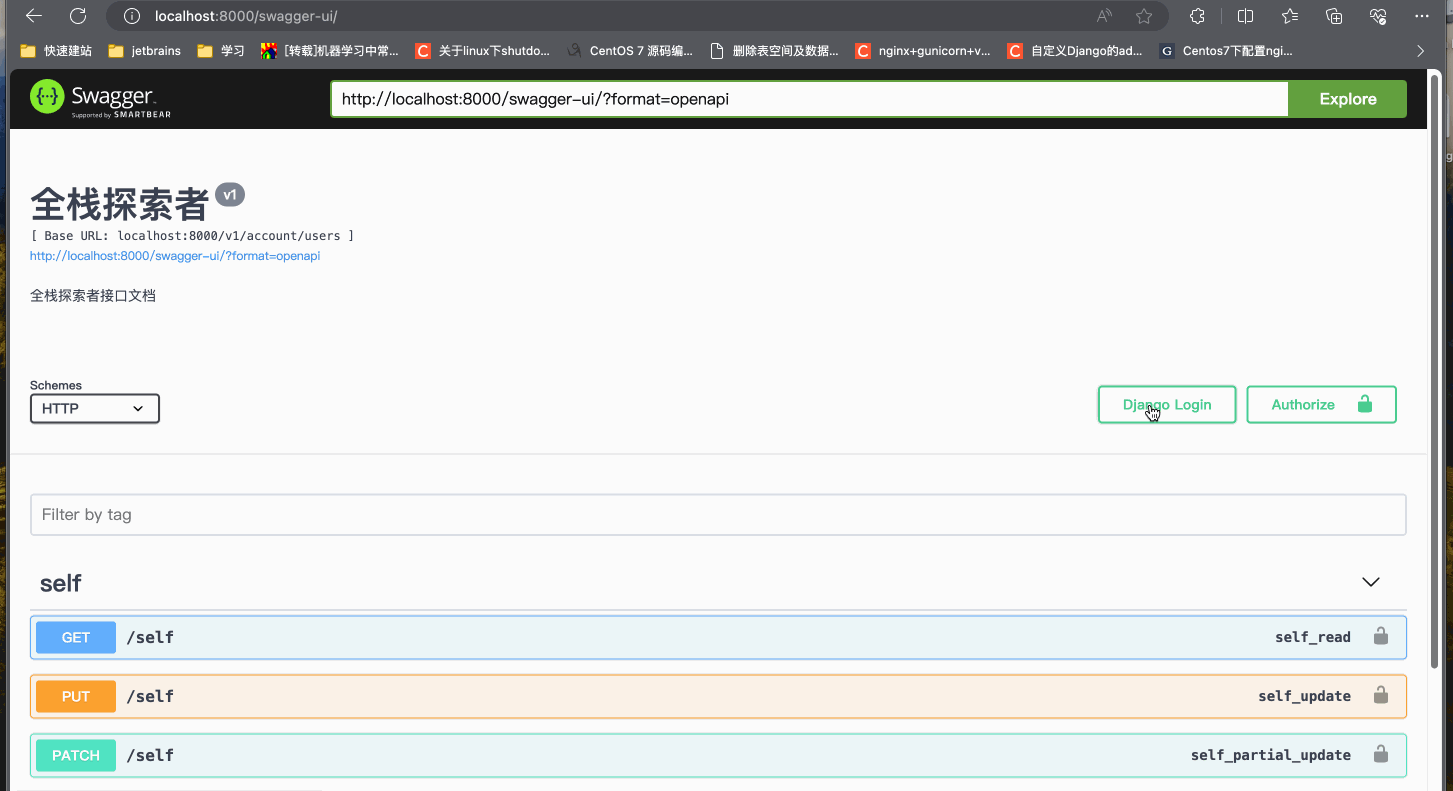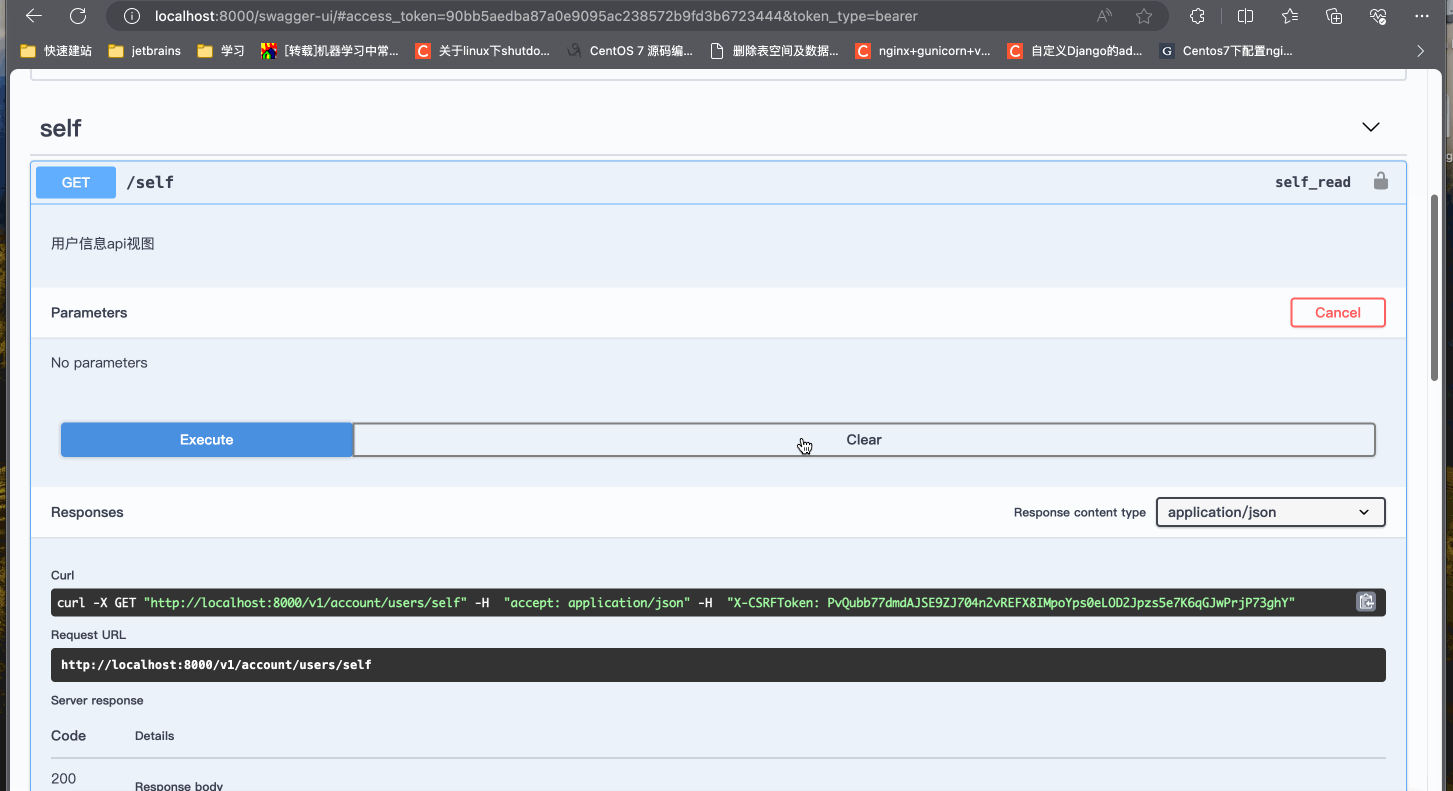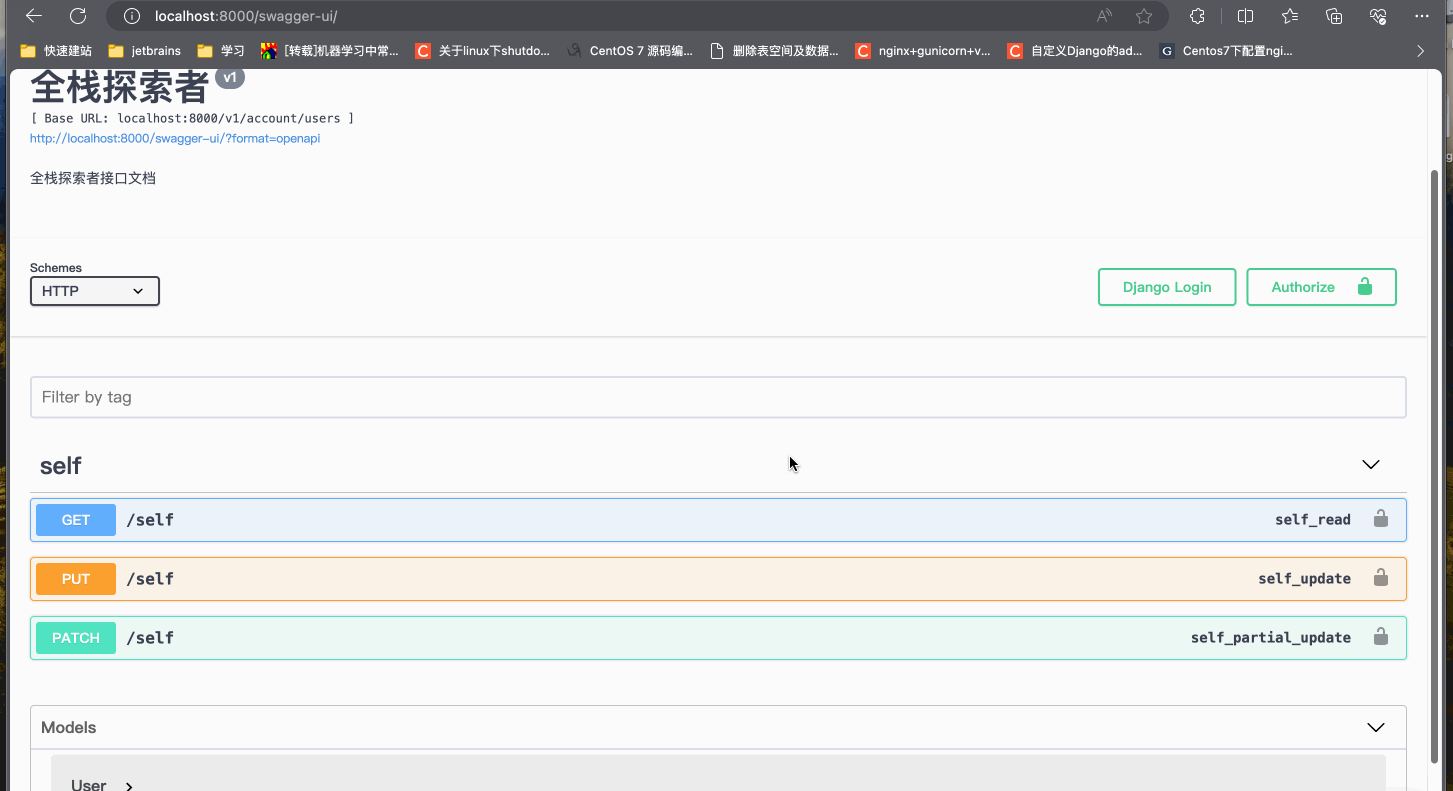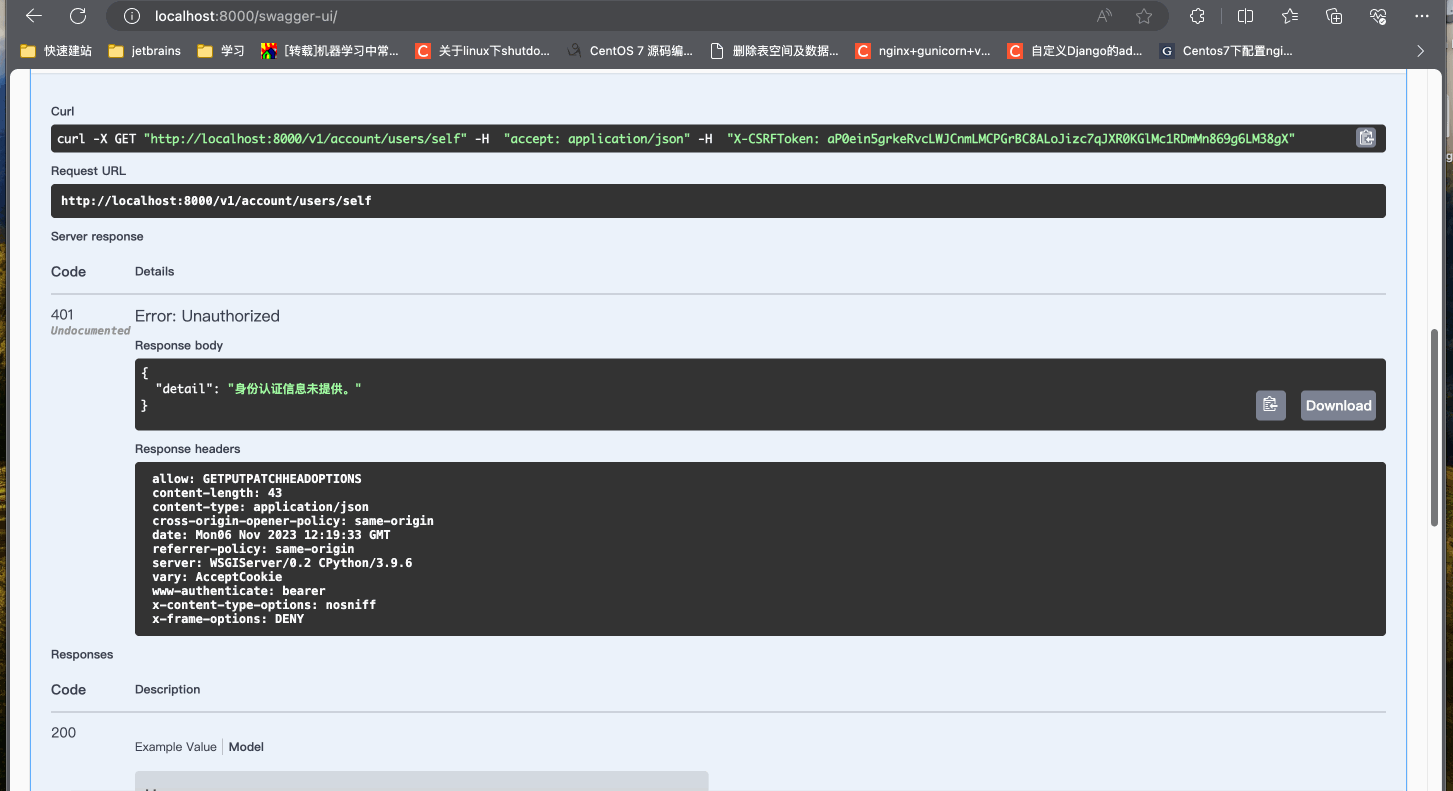
Django初窥门径-oauth登录认证
引言 在现代Web应用程序中,用户身份验证和授权是至关重要的组成部分。Django,一个流行的Python Web框架,为用户身份验证提供了内置支持。本文将探讨如何创建和注册Django应用,自定义身份验证服务,配置AUTHENTICATION_…...

数学到底在哪里支撑着编程?
数学到底在哪里支撑着编程? 除了少数算法等明显相关情况外,说点日常的。 编程是个极度依赖逻辑的领域,逻辑严谨性好,你的编程工作会顺畅很多一-绝大多 数的bug都是最近很多小伙伴找我,说想要一些嵌入式的资料&#x…...

Python模块ADB的, 已经 pyadb
Python模块ADB的使用指南_笔记大全_设计学院 (python100.com) pip install adb Python 调用ADB_python 调用adb命令_实相实相的博客-CSDN博客 Python ADB.shell_command Examples, pyadb.ADB.shell_command Python Examples - HotExamples Gitee 极速下载/PyADB - 码云 - 开…...

猫头虎分享从Python到JavaScript传参数:多面手的数据传递术
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

注解汇总:Spring 常用的注解
前言 本栏目的内容已经讲完了,本案例将把案例中所有讲到的注解都汇总起来,方便日后的学习需要用到的时候能够快速的找到相应的注解。本案例将结合小案例一起做汇总,也想丹玉是再复习一遍讲过用过的注解。 一、注解汇总 1、Component Reposi…...

合肥工业大学操作系统实验5
✅作者简介:CSDN内容合伙人、信息安全专业在校大学生🏆 🔥系列专栏 :hfut实验课设 📃新人博主 :欢迎点赞收藏关注,会回访! 💬舞台再大,你不上台,永远是个观众。平台再好,你不参与,永远是局外人。能力再大,你不行动,只能看别人成功!没有人会关心你付出过多少…...
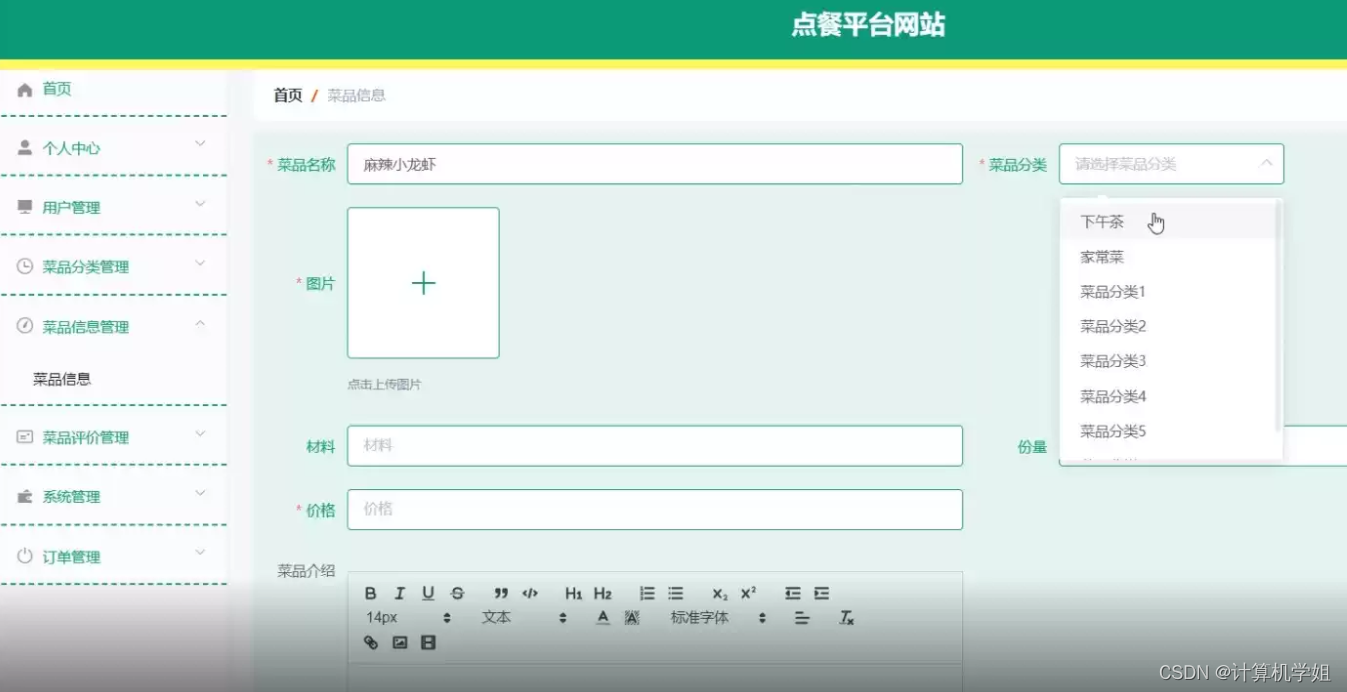
基于SpringBoot+Vue的点餐管理系统
基于springbootvue的点餐平台网站系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 菜品详情 个人中心 订单 管理员界面 菜品管理 摘要 点餐管理系统是一种用…...
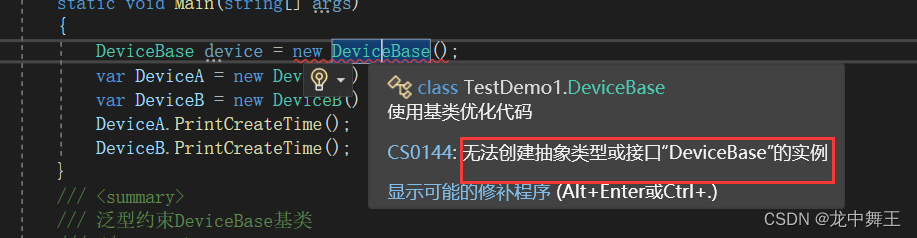
C# 继承,抽象,接口,泛型约束,扩展方法
文章目录 前言模拟需求场景模拟重复性高的需求初始类结构继承优化抽象类 需求1:打印CreateTime方法1:使用重载方法2:基类函数方法3:泛型约束方法3.1:普通泛型方法方法3.2:高级泛型约束,扩展方法…...
mysql的备份和恢复
备份:完全备份 增量备份 完全备份:将整个数据库完整的进行备份 增量备份:在完全备份的基础之上,对后续新增的内容进行备份 备份的需求 1、在生产环境中,数据的安全至关重要,任何数据的都可能产生非常严重…...

【机器学习3】有监督学习经典分类算法
1 支持向量机 在现实世界的机器学习领域, SVM涵盖了各个方面的知识, 也是面试题目中常见的基础模型。 SVM的分类结果仅依赖于支持向量,对于任意线性可分的两组点,它 们在SVM分类的超平面上的投影都是线性不可分的。 2逻辑回归 …...
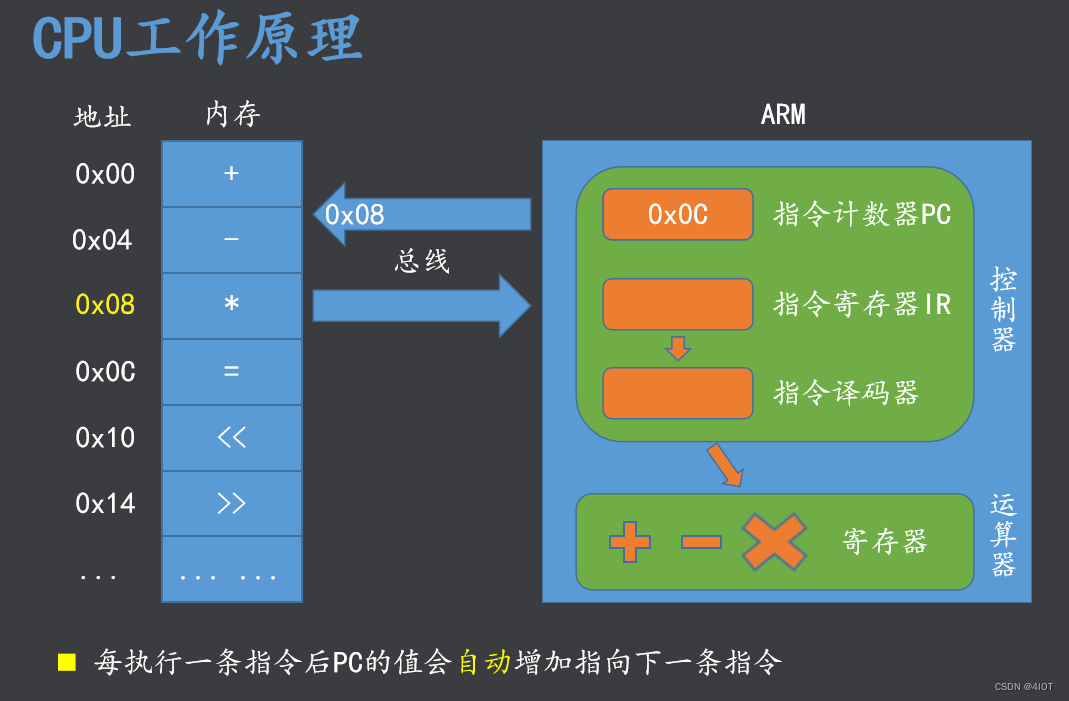
lv11 嵌入式开发 计算机硬件基础 1
目录 1 导学 1.1回顾及导学 1.2 嵌入式系统分层 1.3 linux底层开发 2 ARM体系结构与接口技术课程导学 3 计算机基础 3.1 计算机的进制 3.2 计算机组成 3.3 总线 4 多级存储结构与地址空间 4.1 多级存储概念 4.2 地址空间 5 CPU工作原理 6 练习 1 导学 1.1回顾及导…...
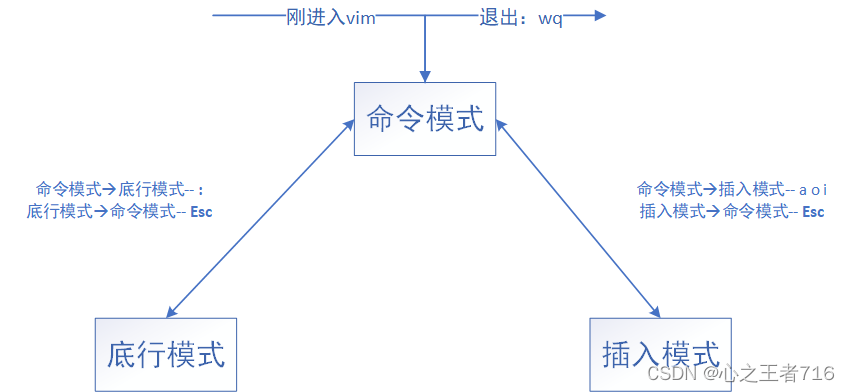
【Linux】vim
文章目录 一、vim是什么?二 、命令模式三、插入模式四、底行模式五、vim配置 一、vim是什么? Vim是一个强大的文本编辑器,它是Vi的增强版,支持多种语法高亮、插件扩展、多模式操作等功能。Vim有三种基本的工作模式:命…...

cstring函数
string 1.char str[]类型 fgets(s,10000,stdin) cin.getline(cin,10000) strlen(str) sizeof 求静态数组长度 2.string类型 getline(cin,a) cin.getline(cin,10000) str.lenth() str.size() cin 遇到空格就停止 3.gets 函数 char str[20]; gets(str); 4.puts 函…...
【owt】p2p client mfc 工程梳理
1年前构建的,已经搞不清楚了。所以梳理下,争取能用较新的webrtc版本做测试。最早肯定用这个测试跑通过 【owt】p2p Signaling Server 运行、与OWT-P2P-MFC 交互过程及信令分析官方的mfc客户端 估计是构造了多个不同的webrc版本的客户端...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
