图论算法:树上倍增法解决LCA问题
文章目录
- 树上倍增法: LCA问题
树上倍增法: LCA问题
树上倍增法用于求解LCA问题是一种非常有效的方法。
倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k
可以发现倍增是呈 2的指数型递增的一类数据,和二分一样,二分是缩小范围的,而倍增是扩大的,因此倍增与二分都具有 logn的时间复杂度,对于求解某些问题是非常高效的。
什么是树的公共祖先?
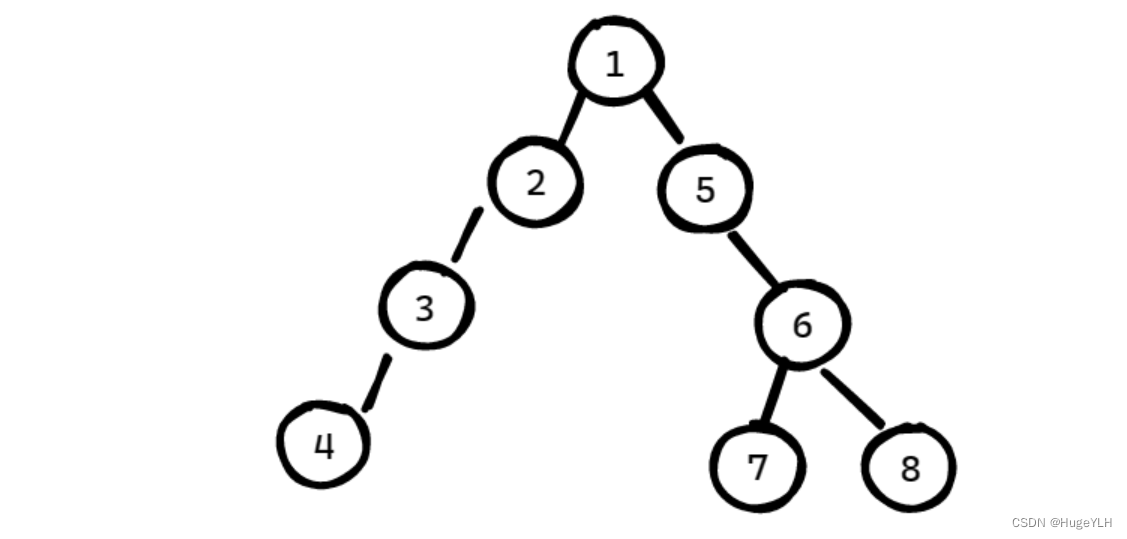
如图所示:
- 节点 7与 节点8的最近公共祖先是 节点6
- 节点3 与 节点5的最近公共祖先是节点1
类似这种问题我们可以使用 树上倍增法来实现
树上倍增的实现:
首先定义 fa[i] [j] 表示 节点编号为 i 的节点,向根节点方向走了 2^j 步所到达的节点
- 什么是走了 2^j 步??
走一条边规定为走了一步,j可以表示为 0 ,1,2 ,分别代表走了 1步,2步,4步
走了一步: 到达了节点6
走了两步: 到达了节点5
走了四步:超过了范围,因此只能到达 节点1
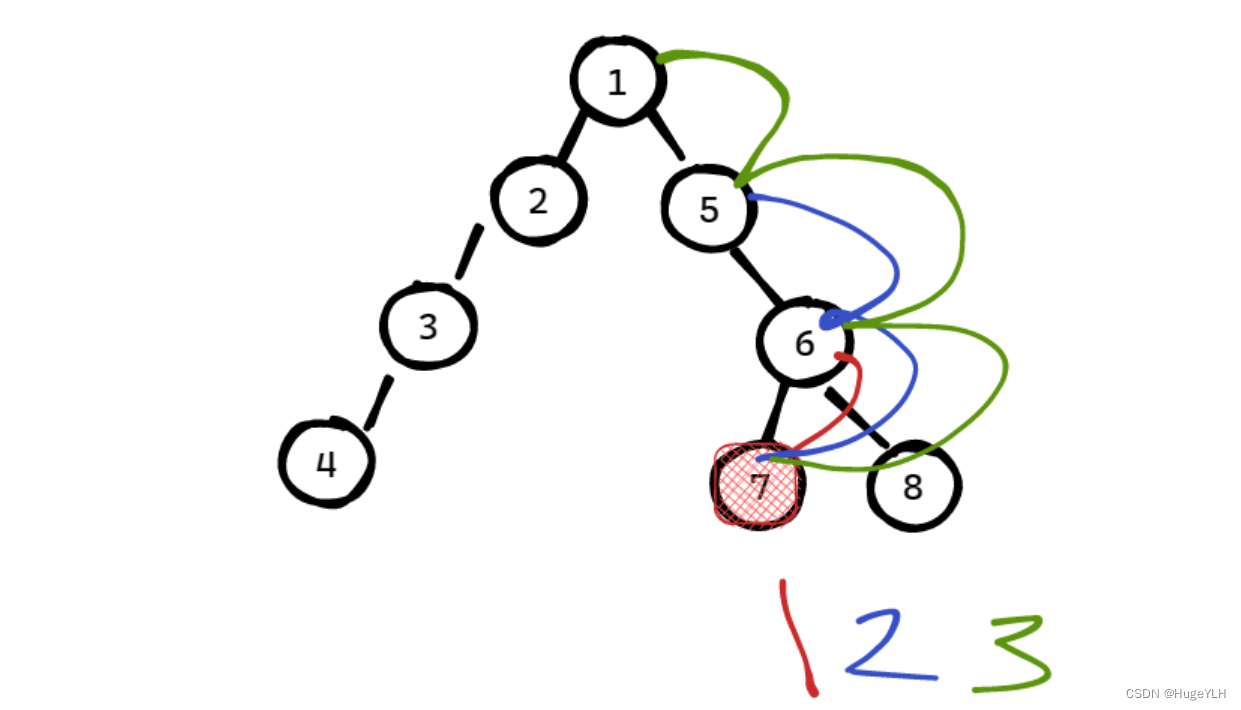
因此我们的 fa数组实际上记录的就是 节点 i 的 第 2^j 个祖先,分别为1:节点6;2:节点5,4:节点1
因此首先把整个树结构存储起来(使用链式前向星)
然后首先对整个图进行预处理
- 预处理的目标:
就是把每个 节点的 第 2^j 个的祖先找出来,用于之后的处理,同时我们还需要记录每个节点的深度,我们采用递归的形式,每次递归,节点的深度都是父节点的深度+1
注意:lg数组预处理每个节点的当前深度+1,可以使得某些地方得到优化
void init(int now,int father)
{fa[now][0]=father;//第now节点的第2^0个父亲节点,即第一个父亲节点是fatherdepth[now]=depth[father]+1;//now的深度是父亲节点深度+1//for (int i=1;i<=lg[depth[now]];i++)for (int i=1;(1<<i)<=depth[now];i++){fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组}//递归预处理当前点的所有子节点for (int i=head[now];i;i=edge[i].next){if (edge[i].to!=father){init(edge[i].to,now);}}
}
寻找LCA的过程:
我们会发现几个问题:
- 两个节点的深度不一样,该如何寻找呢?
- 什么时候寻找结束呢? 即什么时候才能找到他们的LCA 呢
首先来看第一个问题:
深度不同怎么解决? x和y节点
- 我们可以假设 x 节点的深度是最大的。
- 每次让x节点往上移动,直到x节点与y节点到达同一深度
什么时候结束寻找? 即找到了最近公共祖先?
- 当他们位于同一深度的时候,让他们两个节点一起出发,一起往上移动,直到不能再往上移动了为止,他们到达了一个相同的位置,这个节点就是最近公共祖先的节点,返回它即可。
int LCA(int x,int y)
{if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度while (depth[x]>depth[y])//让x与y到达同一深度,倍增x的深度{x=fa[x][lg[depth[x]-depth[y]]-1];}if (x==y) return x;//当他们相同时,LCA就是他们for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数,x与y同时倍增,直到xy到达同一位置{if (fa[x][k]!=fa[y][k]){x=fa[x][k];y=fa[y][k];}}return fa[x][0];//xy到达同一位置,返回父节点
}
模板例题:
最近公共祖先
完整AC code
//TODO: Write code here
int n,m,s;
const int N=1e6+10;
int nums[N];
struct Edge
{int to,w,next;
}edge[N];
int head[N],cnt;
int fa[N][50],depth[N],lg[N];
void add_edge(int u,int v)
{edge[++cnt].next=head[u];edge[cnt].to=v;head[u]=cnt;
}
void init(int now,int father)
{fa[now][0]=father;//第now节点的第2^0个父亲节点,即第一个父亲节点是fatherdepth[now]=depth[father]+1;//now的深度是父亲节点深度+1for (int i=1;i<=lg[depth[now]];i++){fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组}//递归预处理当前点的所有子节点for (int i=head[now];i;i=edge[i].next){if (edge[i].to!=father){init(edge[i].to,now);}}
}
int LCA(int x,int y)
{if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度while (depth[x]>depth[y])//让x与y到达同一深度,倍增x的深度{x=fa[x][lg[depth[x]-depth[y]]-1];}if (x==y) return x;//当他们相同时,LCA就是他们for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数,x与y同时倍增,直到xy到达同一位置{if (fa[x][k]!=fa[y][k]){x=fa[x][k];y=fa[y][k];}}return fa[x][0];//xy到达同一位置,返回父节点
}
signed main()
{cin>>n>>m>>s;for (int i=1;i<=n-1;i++){int u,v;scanf("%lld%lld",&u,&v);add_edge(u,v);add_edge(v,u);}for (int i=1;i<=n;i++){lg[i]=lg[i-1]+(1<<lg[i-1]==i);}init(s,0);for (int i=1;i<=m;i++){int u,v;scanf("%lld%lld",&u,&v);printf("%lld\n",LCA(u,v));}
#define one 1return 0;
}
<<lg[i-1]==i);
}
init(s,0);
for (int i=1;i<=m;i++)
{
int u,v;
scanf(“%lld%lld”,&u,&v);
printf(“%lld\n”,LCA(u,v));
}
#define one 1
return 0;
}
参考:[树上倍增法](https://blog.csdn.net/chengqiuming/article/details/126694822)
相关文章:

图论算法:树上倍增法解决LCA问题
文章目录树上倍增法: LCA问题树上倍增法: LCA问题 树上倍增法用于求解LCA问题是一种非常有效的方法。 倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k 可以发现倍增是呈 2的指数型递增的一类数据,和二分一样&…...
 和 execute()方法有什么区别)
Java线程池中submit() 和 execute()方法有什么区别
点个关注,必回关 文章目录一. execute和submit的区别与联系1、测试代码的整体框架如下:2、首先研究Future<?> submit(Runnable task)和void execute(Runnable command),3、submit(Runnable task, T result) 方法可以使submit执行完Run…...

Vue.extend和VueComponent的关系源码解析
目录 0.概念解释 前言 需求分析 Vue.extend 编程式的使用组件 源码分析 0.概念解释 Vue.extend和VueComponent是Vuejs框架中创建组件的两种不同方式。Vue.extend方法能够让你根据Vue对象(继承)来定义一个新的可重用的组件构造器。而VueComponent方…...
【动态规划】01背包问题(滚动数组 + 手画图解)
01背包除了可以用形象的二维动态数组表示外,还可以使用空间复杂度更低的一维滚动数组。 目录 文章目录 前言 一、滚动数组的基本理解 二、确定dp及其下标含义 三、确定递推公式 四、确定初始化 五、确定遍历顺序 1.用物品(正序)遍历背…...

javaEE 初阶 — 超时重传机制
文章目录超时重传机制1. 数据重复传输问题2. 如何解决数据重复传输问题3. 重传次数问题TCP 的工作机制:确认应答机制 超时重传机制 如果传输数据的时候丢包了该怎么办? 利用 超时重传,也就是超过了一定的时间,如果还没响应就重新…...

小米5x wlan无法打开解决
诱因:想要利用空置设备做节点服务器或者边缘计算,因此解锁并刷了magisk,印象中在刷之前wlan已经无法打开无法进行wifi联网 表现: 1 WLAN开关无法打开,或者虚假打开,无法扫描wifi 2 设置->我的设备->全…...

负载均衡之最小活跃数算法
文章目录[toc]一、概念二、场景与设计思路三、实现四、代码下载一、概念 活跃数 集群中各实例未处理的请求数。 最小活跃数 集群中各个实例,哪个实例未处理的请求数据最小,就称之为最小活跃数。 二、场景与设计思路 场景 以获取微服务地址为场景。 设计…...
JavaScript 评测代码运行速度的几种方法
一、使用 performance.now() API 在 JavaScript 中,可以使用 performance.now() API 来评测代码的运行速度。该 API 返回当前页面的高精度时间戳,您可以在代码执行前后调用它来计算代码执行所需的时间。 例如: let t0 performance.now();…...

Linux 编译器 gcc/g++
本文已收录至《Linux知识与编程》专栏! 作者:ARMCSKGT 演示环境:CentOS 7 目录 前言 正文 gcc/g常用命令 自定义可执行程序名命令-o 预处理指令-E 编译指令-S 汇编指令-c 链接指令gcc 命令巧记口诀 链接库 动态库-动态链接 静态库…...
2.Java基础【Java面试第三季】
2.Java基础【Java面试第三季】前言推荐2.Java基础01_字符串常量Java内部加载-上58同城的java字符串常量池面试code讲解intern()方法---源码解释02_字符串常量Java内部加载-下whyOpenJDK8底层源码说明递推步骤总结考查点03_闲聊力扣算法第一题字节跳动两数求和题目说明面试题解法…...
Java高级-多线程
本篇讲解java多线程 基本概念: 程序、进程、线程 **程序(program)**是为完成特定任务、用某种语言编写的一组指令的集合。即指一段静态的代码,静态对象。 **进程(process)**是程序的一次执行过程,或是正在运行的一个程序。是一个动态的过程…...

mysql高级(事务、存储引擎、索引、锁、sql优化、MVCC)
文章目录1.事务1.1 四大特性ACID1.2 并发事务2.存储引擎2.1 InnoDB2.2 MyISAM2.3 Memory2.4 存储引擎特点2.5 存储引擎的选择3.性能分析3.1 查看执行频次3.2 慢查询日志3.3 profile3.4 explain4.索引4.1 索引结构B-TreeBTreeHash面试题4.2 索引分类思考题4.3 语法4.4 使用规则最…...
Java后端开发功能模块思路
文章目录前言一、查找接口及参数信息1.1 找访问路径1.2 参数及返回结果信息1.3 编写功能模块函数二、代码设计思路三、总结前言 对于正在学习Java后端开发的同学来说,对于Java后端功能模块的开发过程及思路要有一个整体清晰的流程。才能保证在开发过程中更加的顺畅…...
CAPL(vTESTStudio) - DoIP - TCP发送_05
TCP发送 参数定义 版本号:02 FD or 01 FE or 其他任意值数据类型:00 05 or 00 06 or 80 01 or其他任意值数据长度:想要发送的任意长度...
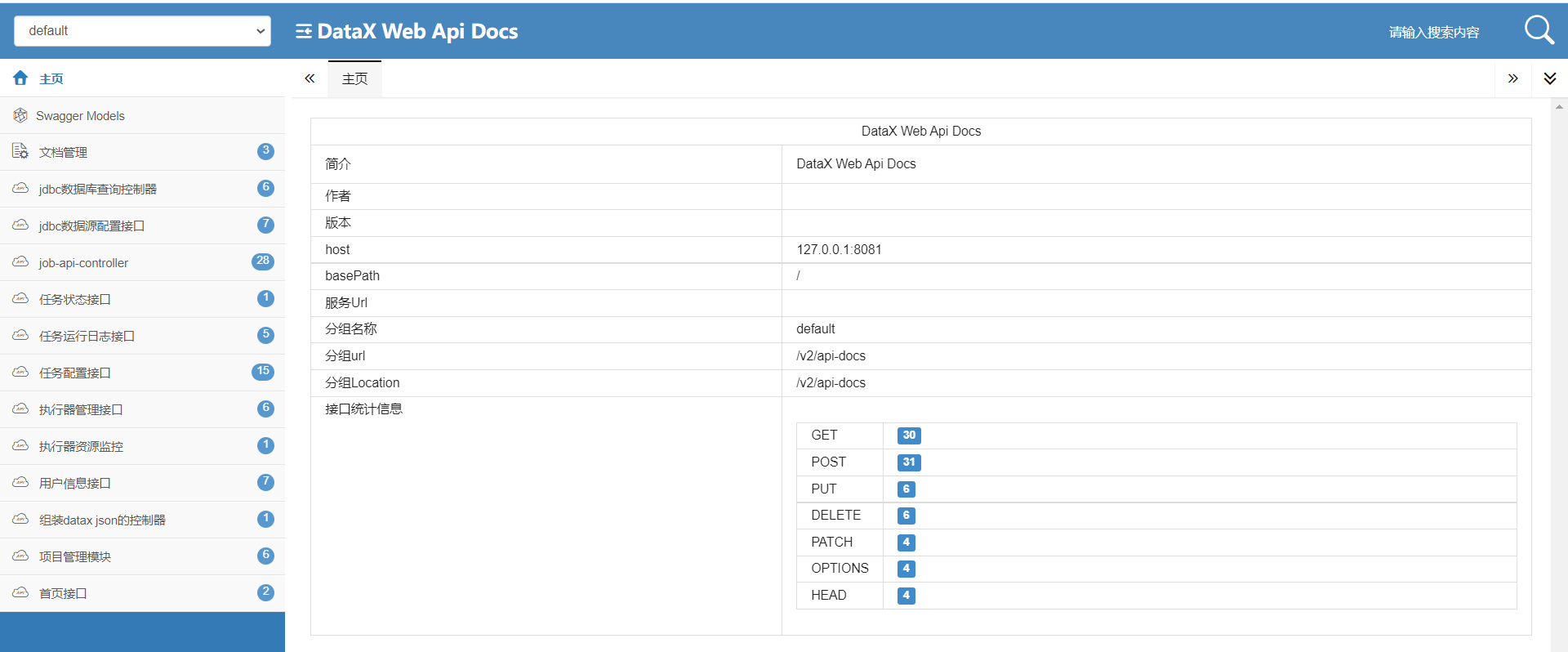
使用IntelliJ IDEA搭建datax-web开发环境
记录:372场景:使用IntelliJ IDEA搭建datax-web开发环境,以及datax-web基本使用。版本:JDK 1.8Python 2.7.5datax-web开源地址:https://github.com/WeiYe-Jing/datax-web1.配置Maven环境1.1安装目录目录:D:\…...

[SSD固态硬盘技术 14] GC垃圾回收太重要了
今天介绍臭名昭著的垃圾收集 过程(或“GC”),maybe 这是对JAVA 工程师而言。当遇到GC导致速度降低时候, 他们真的想跳脚。 我想到我的小孩打疫苗,哭的哇哇叫, 在他的眼里疫苗应该也是讨厌的吧, 但事实真的如此吗? 但首先,让我们考虑一下如果根本没有 GC,闪存系统会发…...
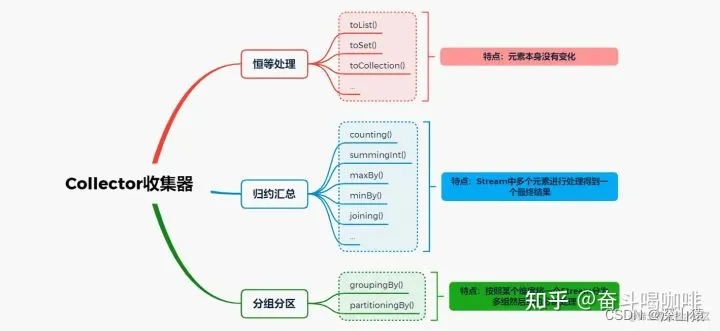
lamada表达式、stream、collect整理
lamada表达式格式 格式:( parameter-list ) -> { expression-or-statements } 实例:简化匿名内部类的写法 原本写法: public class LamadaTest { public static void main(String[] args) { new Thread(new Runnable() { …...
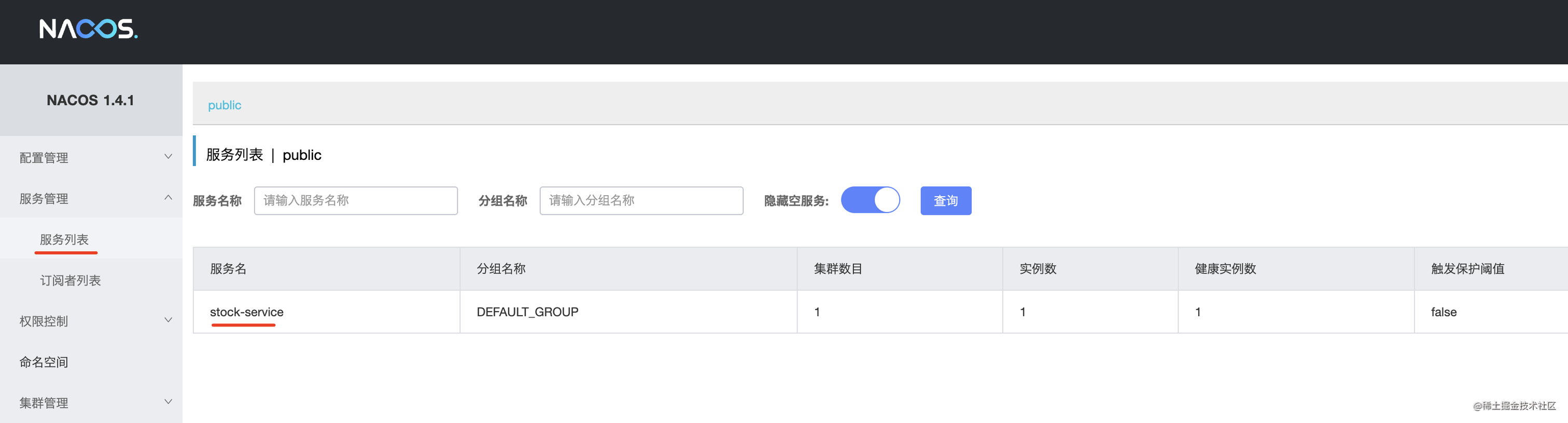
Nacos 入门微服务项目实战
Nacos 核心源码精讲 - IT贱男 - 掘金小册全方位源码精讲,深度剖析 Nacos 注册中心和配置中心的核心思想。「Nacos 核心源码精讲」由IT贱男撰写,375人购买https://s.juejin.cn/ds/BuC3Vs9/ Hi,大家好,欢迎大家来学习《Nacos 核心源…...
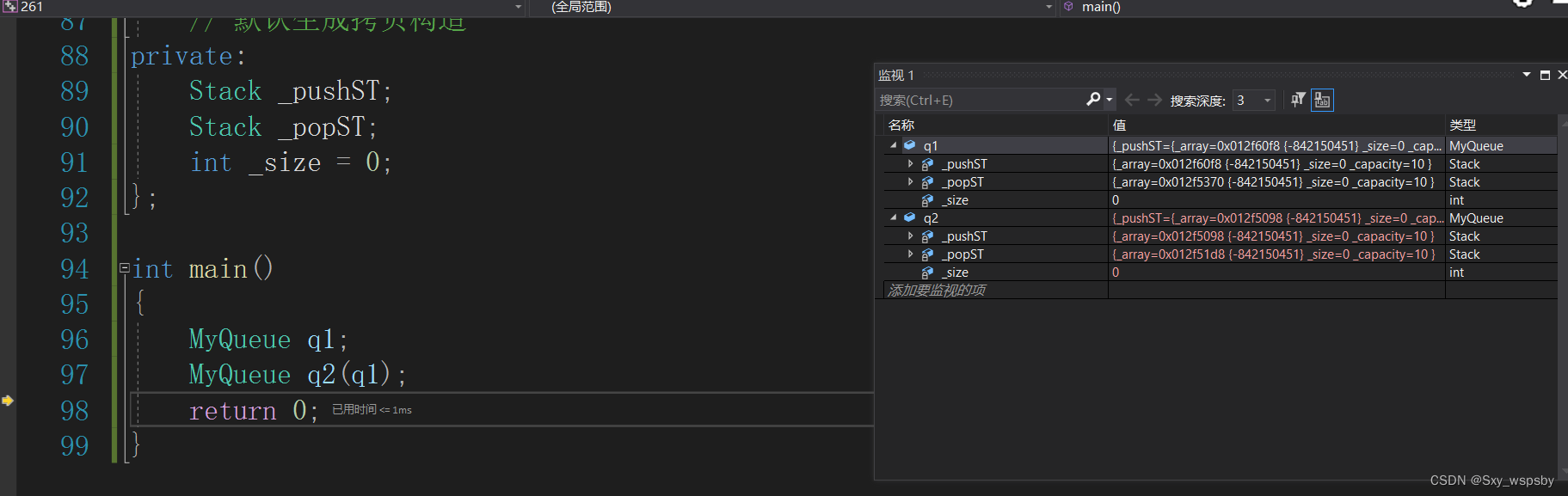
【c++】类和对象:让你明白“面向一个对象有多重要”:构造函数,析构函数,拷贝构造函数的深入学习
文章目录 什么是面向对象?一:类是什么? 1.类的访问限定符 2.封装 3.类的实例化 4.this指针二:类的6个默认成员函数 1.构造函数 2.析构函数 3.拷贝构造函数什么是面向对象? c语言是面向…...

职场IT老手教你3步教你玩转可视化大屏设计,让领导眼前一亮!
我是制造企业的IT中心的研发人员,平常工作就是配合业务部门出出报表,选型一些商业软件,并在内部负责实施运维。最近领导出去参观了一些数字化转型比较领先的工厂和制造企业,回来就甩给我几张图,问能不能我们也做几个这…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
