七大排序(Java)
目录
一、插入排序
1. 直接插入排序
2. 希尔排序
二、选择排序
1. 直接选择排序
2. 堆排序
三、交换排序
1. 冒泡排序
2. 快速排序
四、归并排序
五、总结
一、插入排序
1. 直接插入排序
抓一张牌,在有序的牌中,找到合适的位置并且插入。
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
- 稳定性:稳定

代码:
public static void insertSort(long[] array) {for (int i = 1; i < array.length; i++) {//认为第一个数已经有序,所以循环 n - 1 次long tmp = array[i];int j = i - 1;for(; j >= 0; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}//j回退到了 小于0 的地方array[j + 1] = tmp;}}2. 希尔排序
插入排序的升级版本,即进行大量的分组插排。
- 时间复杂度:O(n^1.3 ~ n^1.5)
- 空间复杂度:O(1)
- 稳定性:不稳定
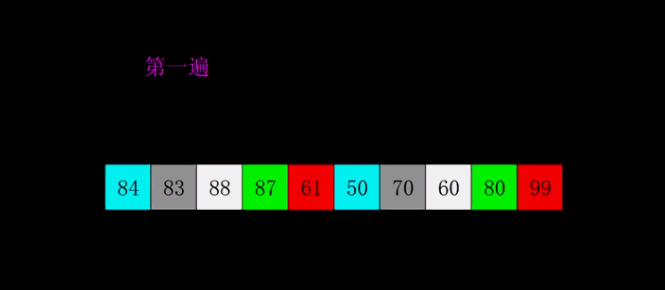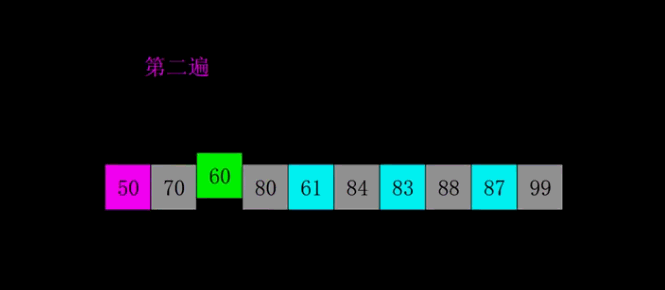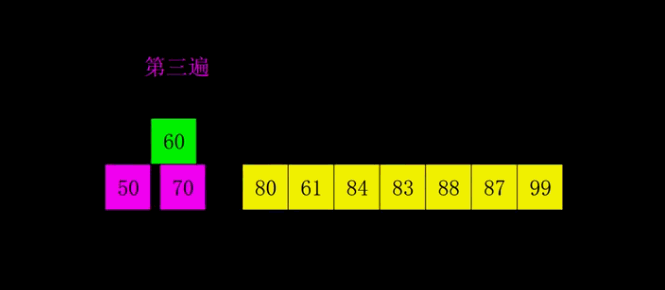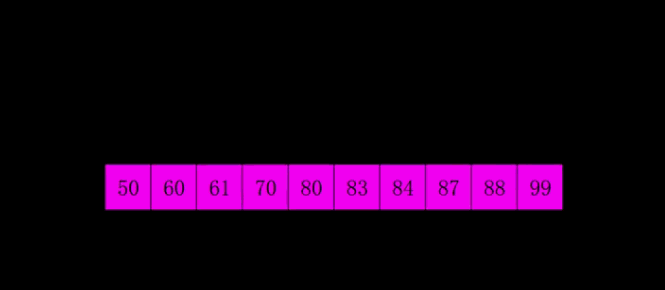
代码:
//gap:组数public static void shell (int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j = j - gap) {if (array[j] > tmp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {shell(array,gap);gap = gap / 2;}shell(array, 1);}
二、选择排序
1. 直接选择排序
找到无序区间中最小的元素的下标,然后将该元素放到无序区间的开始(有序区间的最后)。
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
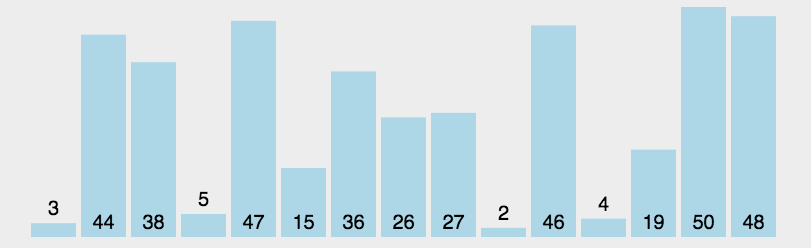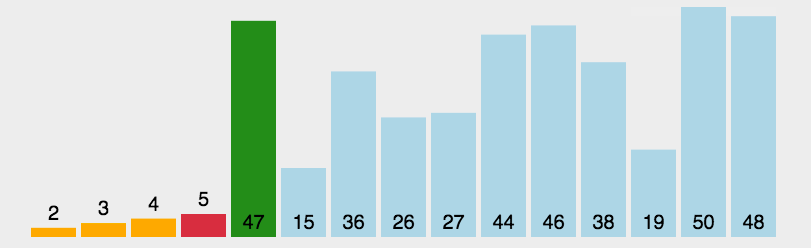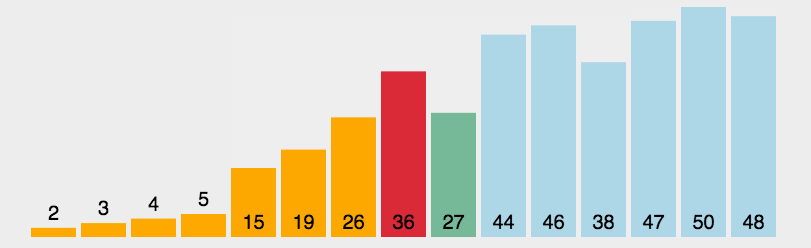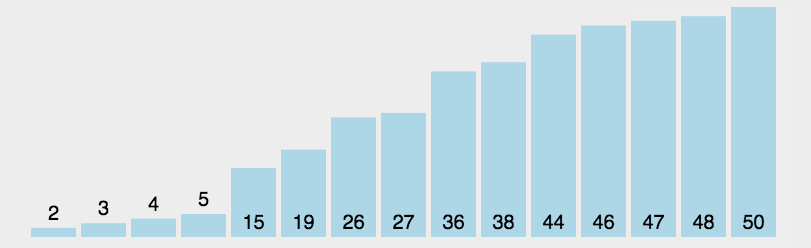
代码:
// array: 待排序区间public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIdx = i;for (int j = i + 1; j < array.length; j++) {if (array[j] < array[i]) {minIdx = j;}}swap(array, minIdx, i);}}2. 堆排序
选择排序的升级版本。将无序区间维护成一个大堆(因为从小到达排序,需要大堆)。利用大堆,从无序区间中找到最大值,交换。
- 时间复杂度:O( N*log(N))
- 空间复杂度:O(1)
- 稳定性:不稳定

代码:
//堆排序public static void heapSort(int[] array) {//1.建堆 O(n)creatHeap(array);int end = array.length - 1;//2.交换然后调整 O(n * log(n))while (end > 0) {swap(array, 0, end);shiftDown(array, 0, end);end--;}}public static void creatHeap(int[] array) {for (int parent = (array.length - 1 - 1)/ 2; parent >= 0; parent--) {shiftDown(array, parent, array.length);}}public static void shiftDown(int[] array, int parent, int len) {int child = 2 * parent + 1; //左孩子下标while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child++;}//child 下标为左右孩子中最大的孩子的下标if (array[child] > array[parent]) {swap(array, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}三、交换排序
1. 冒泡排序
从前往后,两两元素进行比较,前者大于后者则交换。每次循环完一个元素,后面的有序区间就多加一个元素。
- 时间复杂度:O(N^2)
- 有序情况下:O(n)
- 空间复杂度:O(1)
- 稳定性:稳定
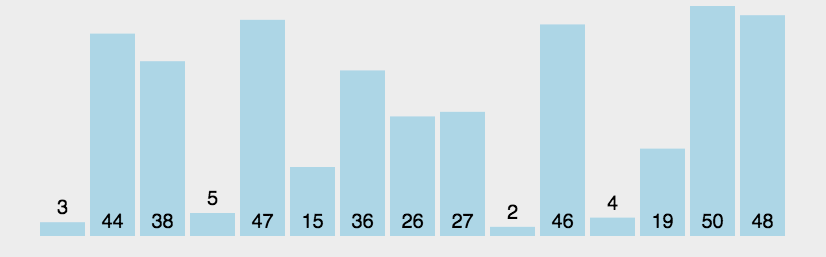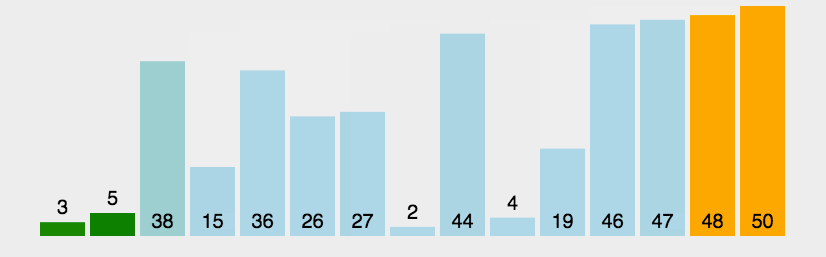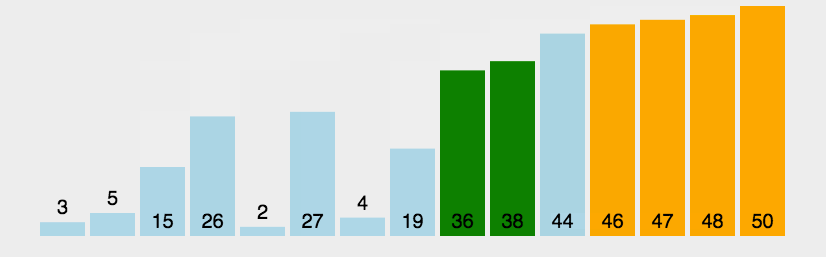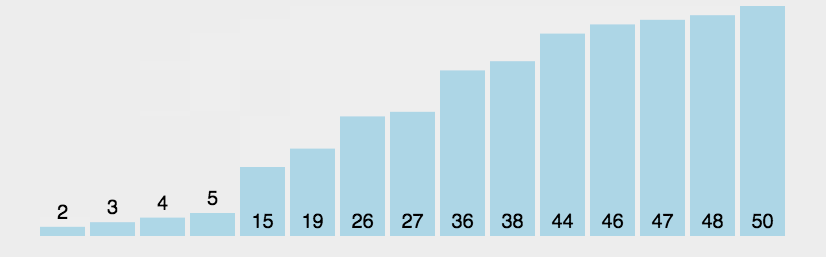
代码:
public static void bubbleSort(int[] array) {for (int i = 0; i < array.length - 1; i++) {boolean flag = false;for (int j = 0; j <array.length - 1 - i; j++) {if (array[j + 1] < array[j]) {swap(array, j, j + 1);flag = true;}}if (flag == false) {break;}}}2. 快速排序
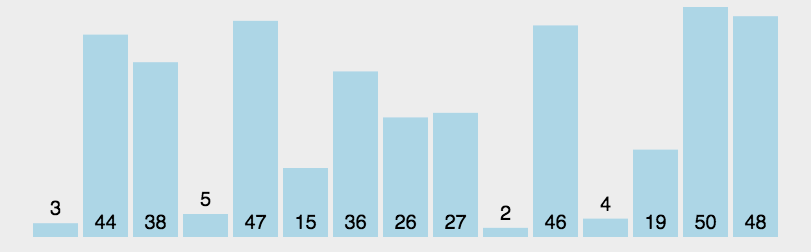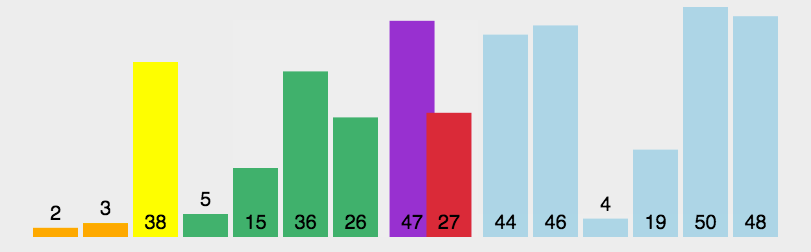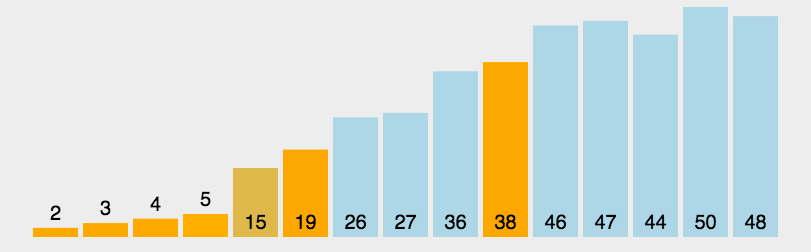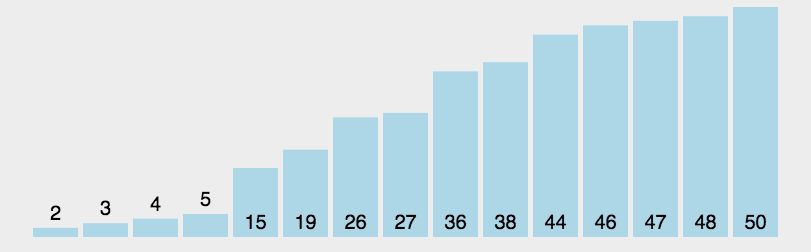
①在待排序区间内,选择一个基准值(pivot),本次代码中选择的是最右边;
②对待排序区间进行 partition 操作,目标:将待排序区间分开,左边的小于等于pivot,右边的大于等于pivot;
③分别再对左右两个小区间按照相同的方式进行处理。
- 时间复杂度:
- 最好【每次可以均匀的分割待排序序列】:O(N*log(N))
- 最坏:数据有序 或者逆序的情况 O(N^2)
- 空间复杂度:
- 最好:O(logN)
- 最坏:O(n) 单分支的一棵树
- 稳定性:不稳定
代码:
public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}public static void quick(int[] array, int left, int right) {if (left >= right) {return;}int pivot = partition(array, left, right);quick(array, left, pivot - 1);quick(array, pivot + 1, right);}//挖坑法public static int partition(int[] array, int start, int end) {int tmp = array[start];while (start < end) {while(start < end && array[end] >= tmp) {end--;}//end位置的元素小于基准值,挖坑array[start] = array[end];while(start < end && array[start] <= tmp) {start++;}//start位置的元素大于基准值,挖坑array[end] = array[start];}array[start] = tmp;return start;}由于用到了递归,当基准值左右边已经有序时,还需要栈空间来进行递归,所以当数据过大时,可能会导致栈溢出的情况,所以要将快速排序进行优化。
- 当待排序区间元素个数小于某个范围时,可以使用插入排序。
- 找基准值时,采用三数取中法。
代码:
public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}public static void quick(int[] array, int left, int right) {if (left >= right) {return;}//优化1:元素小于某个区间时,使用插入排序if (right - left + 1 < 1400) {insertSort(array, left, right);}//优化2:三数取中法int MinIdx = FindMinIdx(array, left, right);swap(array, MinIdx, left);int pivot = partition(array, left, right);quick(array, left, pivot - 1);quick(array, pivot + 1, right);}//挖坑法public static int partition(int[] array, int start, int end) {int tmp = array[start];while (start < end) {while(start < end && array[end] >= tmp) {end--;}//end位置的元素小于基准值,挖坑array[start] = array[end];while(start < end && array[start] <= tmp) {start++;}//start位置的元素大于基准值,挖坑array[end] = array[start];}array[start] = tmp;return start;}//插入排序public static void insertSort(int[] array, int start, int end) {for (int i = 1; i < end; i++) {int tmp = array[i];int j = i - 1;for (; j >= start; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {//array[j + 1] = tmpbreak;}}// j 回退到了小于 0 的位置//或者从 break 出来array[j + 1] = tmp;}}//三数取中法private static int FindMinIdx(int[] array, int start, int end) {int mid = start + ((end - start) >>> 1);if (array[start] < array[end]) {if (array[mid] < array[start]) {return start;} else if (array[mid] > array[end]) {return end;} else {return mid;}} else {if (array[mid] > array[start]) {return start;} else if (array[mid] < array[end]) {return end;} else {return mid;}}}public static void swap(int[] array, int p, int q) {int tmp = array[p];array[p] = array[q];array[q] = tmp;}快速排序非递归版本:利用栈存储 left 和 right 的值。
public static void quickSort非递归(int[] array) {Deque<Integer> stack = new LinkedList<>();int left = 0;int right = array.length - 1;int pivot = partition(array, left, right);if (pivot > left + 1) {//左边有两位数stack.push(left);stack.push(pivot - 1);}if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}while(!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition(array, left, right);if (pivot > left + 1) {//左边有两位数stack.push(left);stack.push(pivot - 1);}if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}}四、归并排序
归并排序是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
- 时间复杂度:O(N*log(N))
- 空间复杂度:O(n)
- 稳定性:稳定

在写归并排序代码之前,需要先会写:两个有序数组合并为一个有序数组。
代码:
//将两个有序数组合并为一个有序数组//array1 和 array2 均为有序数组public static int[] mergeArray(int[] array1, int[] array2) {int[] tmp = new int[array1.length + array2.length];int s1 = 0;int s2 = 0;int e1 = array1.length - 1;int e2 = array2.length - 1;int k = 0;while (s1 <= e1 && s2 <= e2){if (array1[s1] <= array2[s2]) {tmp[k++] = array1[s1++];//k++;//s1++;} else {tmp[k++] = array2[s2++];}}while (s1 <= e1) {tmp[k++] = array1[s1++];}while (s2 <= e2) {tmp[k++] = array2[s2++];}return tmp;}归并排序代码:
public static void mergeSort(int[] array) {mergeSortInternal(array, 0, array.length - 1);}private static void mergeSortInternal(int[] array, int low, int high) {if (low >= high) {return;}int mid = low + ((high - low) >>> 1);mergeSortInternal(array, low, mid);mergeSortInternal(array, mid + 1, high);merge(array, low, mid, high);}public static void merge(int[] array, int low, int mid, int high) {int[] tmp = new int[high - low + 1];int k = 0;int s1 = low;int e1 = mid;int s2 = mid + 1;int e2 = high;while (s1 <= e1 && s2 <= e2) {if (array[s1] <= array[s2]) {tmp[k++] = array[s1++];} else {tmp[k++] = array[s2++];}}while (s1 <= e1) {tmp[k++] = array[s1++];}while (s2 <= e2) {tmp[k++] = array[s2++];}//普通的归并数组需要直接返回 tmp 数组//但是在归并排序中,要将 tmp 数组重新拷贝到 array 数组中,//并且考虑在右子树中合并时,不能覆盖左边已经合并好的元素for (int i = 0; i < k; i++) {array[low + i] = tmp[i];}}非递归版本:
public static void mergeSort非递归(int[] array) {int nums = 1; //每组的数据个数while (nums < array.length) {for (int i = 0; i < array.length; i++) {int left = i;int mid = left + nums - 1;//防止越界if (mid >= array.length) {mid = array.length - 1;}int right = mid + nums;//防止越界if (right >= array.length) {right = array.length - 1;}//下标确定之后进行合并merge(array, left, mid, right);}nums *= 2;}}五、总结
七大排序中:
稳定的排序:冒泡排序、插入排序、归并排序
插入排序主要看数组是否有序,来影响其时间复杂度
归并排序无论什么情况下,时间复杂度都为 O(N*log(N))
时间复杂度为O(N*log(N))的排序:快速排序、堆排序、归并排序
要想速度快就选 快速排序
要想稳定就选 归并
要想空间复杂度低就选 堆排序
| 排序 | 时间复杂度 | 空间复杂度 | 稳定性 |
| 插入排序 | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N^1.3) | O(1) | 不稳定 |
| 选择排序 | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*log(N)) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(1) | 稳定 |
| 快速排序 | O(N*log(N)) | O(log(N)) | 不稳定 |
| 归并排序 | O(N*log(N)) | O(n) | 稳定 |
相关文章:

七大排序(Java)
目录 一、插入排序 1. 直接插入排序 2. 希尔排序 二、选择排序 1. 直接选择排序 2. 堆排序 三、交换排序 1. 冒泡排序 2. 快速排序 四、归并排序 五、总结 一、插入排序 1. 直接插入排序 抓一张牌,在有序的牌中,找到合适的位置并且插入。 时间…...

分享一些可以快速掌握python语法的小技巧
下面是我总结的一些有助于快速掌握 Python 语法的小技巧,欢迎一起交流。 注释:在代码中添加注释可以帮助你和其他人理解代码的目的和功能。在 Python 中,使用 # 符号来添加单行注释,使用三引号 """ 或 来添加多行…...
1.FFmpeg-音视频基础
专栏介绍基于最新的FFmpeg5.1.2版本讲解学习, 跟随博主一起学习ffmpeg: 本专栏学习流程为: FFmpeg安装、...
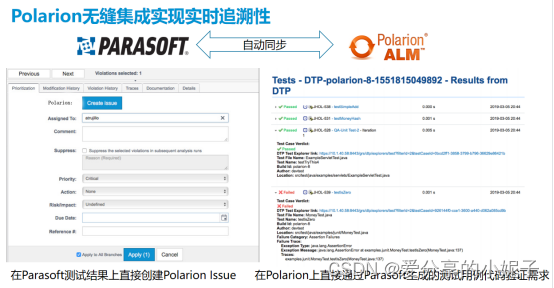
Parasoft的自动化测试平台到底强在哪?
在如今产品迭代如此之快的大背景下,软件测试这项工作越来越被大家所重视,但是通常情况下大家都是选择在产品上线前再去做测试,这个时候就会面临很多麻烦和挑战。首先,产品已经开发好之后,体量比较大,要从哪…...
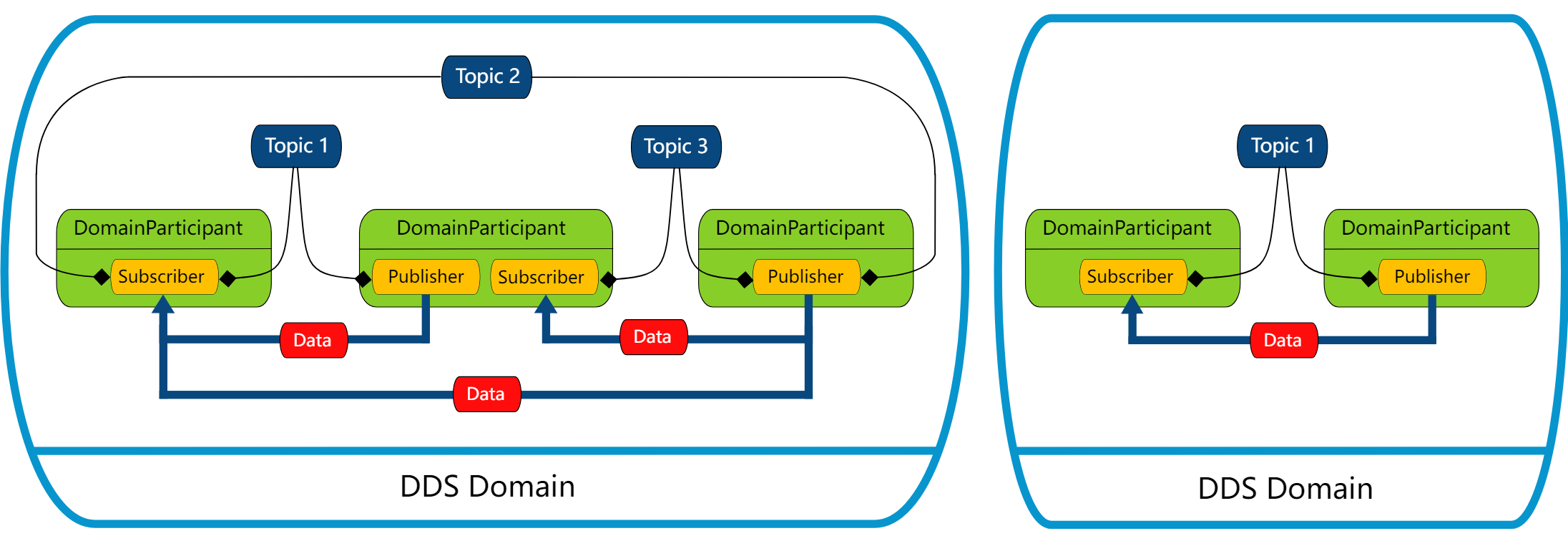
FastDDS-0.简介
FastDDS简介 eProsima Fast DDS 是 DDS (Data Distribution Service) 协议的一个C语言实现版本,该协议由 Object Management Group (OMG) 组织定义。 eProsima Fast DDS 库既提供了一个应用编程接口(API),又提供了一种通信协议&a…...
Flutter入门进阶之旅 -开源Flutter项目
开源Flutter项目 该项目为纯flutter端项目,采用aar方式寄生在原生APP中,作为APP中的一个独立模块 在业务逻辑上做到与原生APP完全隔离,Flutter端开发者,可完全不用关注原生端的业务模块 两端开发彼此业务隔离,缩小了对…...
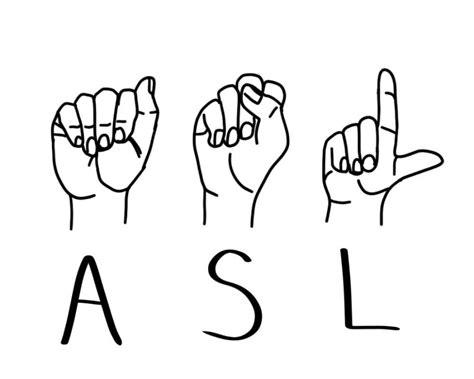
Opencv项目实战:21 美国ASL手势识别
0、项目介绍 首先,我可以保证在这里,你并不需要多么了解深的机器学习算法,我的初衷是通过本项目,激发大家学习机器学习的动力。选择这种手势原因是因为只有24个字母,你的电脑足以带的动,虽然我只训练A、B、…...

强化学习RL 01: Reinforcement Learning 基础
目录 RL理解要点 1. RL数学基础 1.1 Random Variable 随机变量 1.2 概率密度函数 Probability Density Function(PDF) 1.3 期望 Expectation 1.4 随机抽样 Random Sampling 2. RL术语 Terminologies 2.1 agent、state 和 action 2.2 策略 policy π 2.3 奖励 reward …...

C语言之练习题合集
💗 💗 博客:小怡同学 💗 💗 个人简介:编程小萌新 💗 💗 如果博客对大家有用的话,请点赞关注再收藏 🌞 文章目录leetcode 题号:728. 自除数leetcode 题号:238.…...
sublimeText3新建文件自动添加注释头
参考: https://github.com/shiyanhui/FileHeader/blob/master/README.rst https://packagecontrol.io/packages/FileHeader https://github.com/shiyanhui/FileHeader fileheader:https://codeload.github.com/shiyanhui/FileHeader/zip/refs/heads/m…...

AndroidStudio打包HBuilderX的H5+项目为安卓App【一次过,无任何异常报错】
目录 1.查看HBuilderX的版本号 2.下载Dcloud上对应的安卓SDK 3.下载完安卓SDK后,我们解压它,注意不要放在任何有中文组成的文件夹中【是否有中文决定于你鼠标单击上面路径后,第一张图还没鼠标单击,第二张已鼠标单击,…...

【Linux】进程概念
目录 一、基本概念 二、查看进程 三、系统调用获取进程标示符 1、获取自己的PID 2、获取父进程的PID 四、创建进程 1、初识fork 2、使用fork的方式 五、进程状态 1、阻塞 2、挂起 3、R状态 4、S状态 5、D状态 6、T状态 6.1、kill指令 6.2、暂停进程与继续进程 …...

使用pyinstaller库打包exe时显示KeyError怎么办
PyInstaller是一个Python库,用于将Python应用程序转换为独立的可执行文件(executable)文件,支持多平台。它可以将Python解释器、依赖的库和脚本打包成一个单独的可执行文件,从而使应用程序可以独立运行,而无…...

k8s新增节点机器,无法拉取和推送镜像的解决方案
1、首先检查配置,查看镜像仓库是否已授权,若无授权,则进行授权。 命令:cat /etc/systemd/system/docker.service.d/docker-options.conf内容如果有这样一句就是已经授权,如果没有,就需要把这句加进去&…...

测试报告踩坑的点
测试报告作为测试人员的核心输出项,是体现自己工作价值的重要承载工具,需要我们认真对待,所以我们要重视测试报告的输出,那么在编写测试报告的时候,我们有哪些点需要注意的呢? 01 不要乱用模板 很多测试新人在编写测试…...
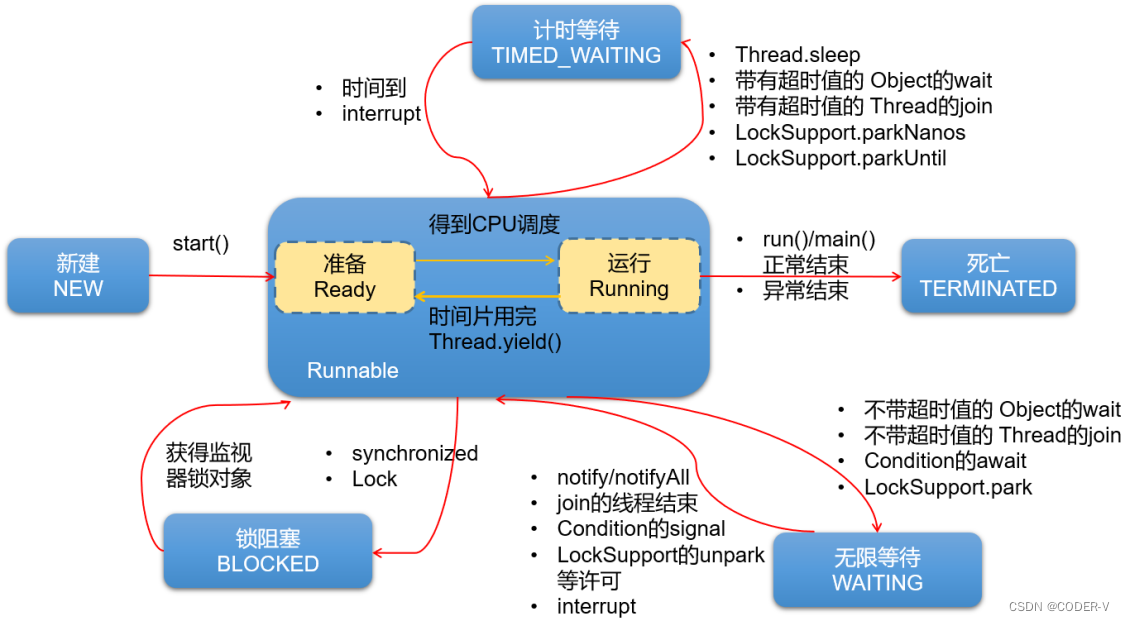
【Java】创建多线程的四种方式
一、方式1:继承Thread类 步骤: 创建一个继承于Thread类的子类重写Thread类的run()方法 ----> 此线程执行的操作声明在方法体中创建当前Thread子类的对象通过实例对象调用start()方法,启动线程 ----> Java虚拟机会调用run()方法 注意…...

【数据结构】队列的接口实现(附图解和源码)
队列的接口实现(附图解和源码) 文章目录队列的接口实现(附图解和源码)前言一、定义结构体二、接口实现(附图解源码)1.初始化队列2.销毁队列3.队尾入队列4.判断队列是否为空5.队头出队列6.获取队列头部元素7…...

日本知名动画公司东映动画加入 The Sandbox 元宇宙
与 Minto 合作将东映动画的 IP 呈现在元宇宙。 The Sandbox 很荣幸能与东映动画合作,与 Minto 携手在 The Sandbox 元宇宙中创建基于东映动画 IP 的相关体验。 作为日本动画的先驱,东映动画制作了日本最大和世界领先的动画作品,包括《龙珠》、…...

QuickHMI Hawk R3 Crack
基于网络的 SCADA / HMI 系统 QuickHMI Hawk R3 QuickHMI是一个 100% 基于网络的SCADA/HMI 系统。 得益于HTML5、SVG和Javascript等现代网络技术,可视化可以在任何当前浏览器和设备中显示。作为浏览器的替代品,可以使用“独立查看器”和移动应用程序。 Q…...

【C语言】寻找隐藏字母游戏
编程实现一个游戏程序,会将连续三个字母中的一个隐去,由玩家填写隐去的那个字母,如屏幕上显示A ? C,则玩家需要输入B;屏幕上显示?B C,则玩家需要输入A。记录玩家完成20次游戏的时间以及正确率。…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
