原始GAN-pytorch-生成MNIST数据集(原理)
文章目录
- 1. GAN 《Generative Adversarial Nets》
- 1.1 相关概念
- 1.2 公式理解
- 1.3 图片理解
- 1.4 熵、交叉熵、KL散度、JS散度
- 1.5 其他相关(正在补充!)
1. GAN 《Generative Adversarial Nets》
Ian J. Goodfellow, Jean Pouget-Abadie, Yoshua Benjio etc.
https://dl.acm.org/doi/10.5555/2969033.2969125
1.1 相关概念
生成模型:学习得到联合概率分布P(x,y)P(x,y)P(x,y),即特征x和标签y同时出现的概率,然后可以求条件概率分布和其他概率分布。学习到的是数据生成的机制。
判别模型: 学习得到条件概率分布P(y∣x)P(y|x)P(y∣x),即在特征x出现的情况下标记y出现的概率
学习一个分布和近似一个分布?
1.2 公式理解
GAN的似然函数(损失函数还要加上一个负号哦):
minGmaxDV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))](1.1)\underset{G}{min}\underset{D}{max}V(D,G) = E_{x \sim P_{data}(x)}[log D(x)]+E_{z\sim p_{z}(z)}[log(1-D(G(z)))] \tag{1.1}GminDmaxV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))](1.1)
为了学习数据x的分布pgp_gpg,定义了一个含有噪声的变量分布pz(z)p_z(z)pz(z);V是评分方程(这个值是越大越好的),G是一个生成器,D是一个判别器;训练D最大化真实数据和生成数据的区别,训练G最小化真实数据和生成数据的区别;
注意这个公式有两项,第一项是指是否能正确识别真实的数据;第二项是指是否能够识别生成的数据;
(1) 完美D
- 当D(x)D(x)D(x)完美识别真实数据和生成数据,Ex∼Pdata(x)[logD(x)]E_{x\sim P_{data}(x)}[log D(x)]Ex∼Pdata(x)[logD(x)]趋近于1,而Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]趋近于0,整体趋近于1.
- 当DDD不完美的时候,由于存在logloglog会使得两项都是一个负数;那训练的目的就是使得这个负数尽量小
- 因此需要最大化判别器带来的值,来使得判别器D最佳。
(2) 完美G
- G只和Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]相关,如果G完美忽悠D的时候,Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]输出的结果就是负无穷;
- 当不是那么完美的时候,输出的值就是一个负数;我们目的是使得这个输出尽量小,以使得生成器最佳。
- 所以需要最小化生成器带来值Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]
训练过程
训练D说明
生成器生成的数据就是V(G,D)的第二项的输入:g(z)=xg(z) = xg(z)=x,那么对z的求和就可以变为对x的求和。
将V(G,D)V(G,D)V(G,D)展开成积分/求和的形式
V(G,D)=∫xpdata⋅log(D(x))dx+∫zpz(z)⋅log(1−D(g(z)))=∫xpdata⋅log(D(x))+pg(x)⋅log(1−D(x))dx(1.2)\begin{aligned} V(G,D) &= \int_x p_{data} \cdot log(D(x))dx + \int_z p_z(z) \cdot log(1-D(g(z))) \\ &=\int_x p_{data} \cdot log(D(x)) + p_g(x) \cdot log(1-D(x))dx \end{aligned} \tag{1.2} V(G,D)=∫xpdata⋅log(D(x))dx+∫zpz(z)⋅log(1−D(g(z)))=∫xpdata⋅log(D(x))+pg(x)⋅log(1−D(x))dx(1.2)
对于 任意的(a,b)∈R2\{0,0}(a,b) \in R^2 \backslash \{0,0\}(a,b)∈R2\{0,0},函数y→alog(y)+blog(1−y)y \rightarrow a log(y) + blog(1-y)y→alog(y)+blog(1−y)是一个凸函数,我们需要求这个函数的最大值,就求导数
ay+b1−y=0y=aa+b\begin{aligned} \frac{a}{y}+\frac{b}{1-y} = 0 \\ y = \frac{a}{a+b} \end{aligned} ya+1−yb=0y=a+ba
则在y=aa+by = \frac{a}{a+b}y=a+ba的时候有最大值,对应于判别器的概率即为:
DG∗(x)=pdata(x)pdata(x)+pg(x)D_G^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}DG∗(x)=pdata(x)+pg(x)pdata(x)
将最优解带入到价值函数之中
C(G)=maxDV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logpdata(x)pdata(x)+pg(x)]+Ex∼pg[logpg(x)pdata(x)+pg(x)](1.3)\begin{aligned} C(G) &= \underset{D}{max}V(G,D) \\ &= E_{x \sim p_{data}}[log D_G^*(x)] + E_{z \sim p_z}[log(1-D_G^*(G(z)))] \\ &= E_{x \sim p_{data}}[log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}] + E_{x \sim p_g}[log \frac{p_g(x)}{p_{data}(x) + p_g(x)}] \end{aligned} \tag{1.3} C(G)=DmaxV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logpdata(x)+pg(x)pdata(x)]+Ex∼pg[logpdata(x)+pg(x)pg(x)](1.3)
根据KL散度和JS散度的定义,可以将上面的公式改写为
C(G)=KL(Pdata∣∣pdata+pg2)+KL(pg∣∣pdata+pg2)−log(4)=2⋅JSD(pdata∣∣pg)−log(4)(1.4)\begin{aligned} C(G) &= KL(P_{data} || \frac{p_{data}+p_g}{2}) + KL(p_g || \frac{p_{data}+p_g}{2}) -log(4) \\ &= 2 \cdot JSD(p_{data}||p_g) - log(4) \end{aligned} \tag{1.4} C(G)=KL(Pdata∣∣2pdata+pg)+KL(pg∣∣2pdata+pg)−log(4)=2⋅JSD(pdata∣∣pg)−log(4)(1.4)
注意pdata+pg2\frac{p_{data}+p_g}{2}2pdata+pg这里除以2是为了保证是一个分布(即概率的积分是等于1的)
在固定D训练G的时候,我们就是为了最小化这个C(G)C(G)C(G),根据上面推导:
所以给出结论:当pg=pdp_g = p_dpg=pd时,DG∗(x)=12D_G^*(x) = \frac{1}{2}DG∗(x)=21,因此C(G)=log12+12=−log4C(G) = log\frac{1}{2} + \frac{1}{2} = -log4C(G)=log21+21=−log4,可以得到最小的C(G)C(G)C(G)
1.3 图片理解
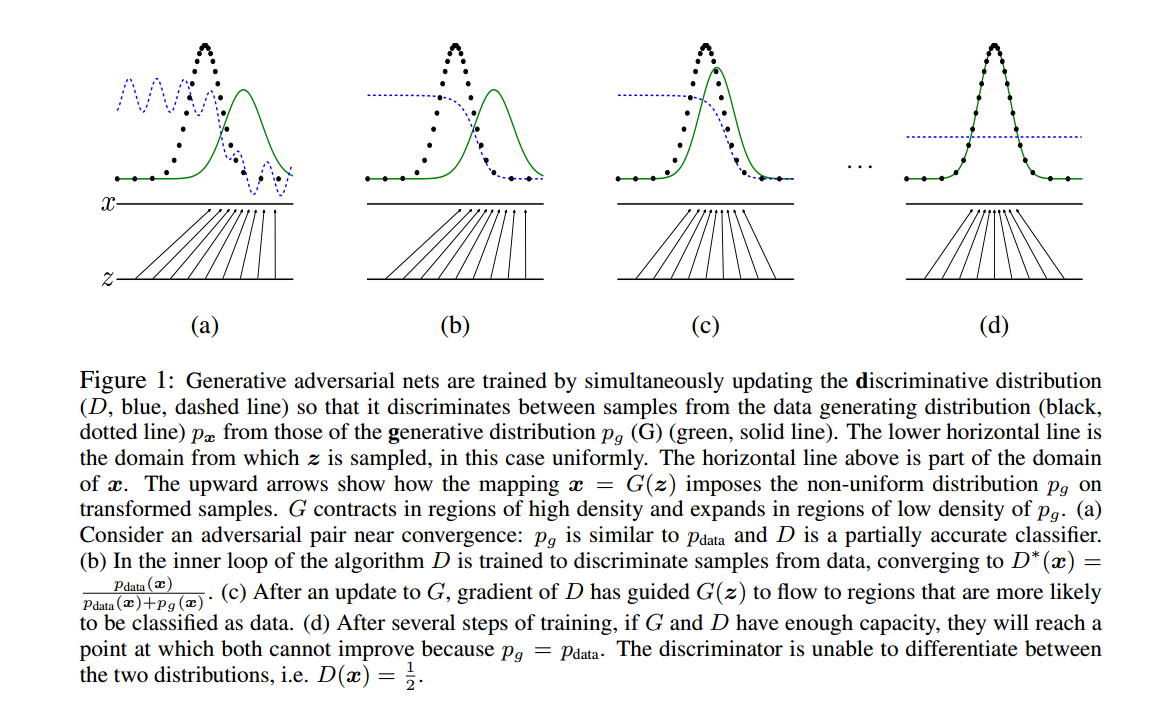
绿色是生成的分布;黑色是真实分布;蓝色是判别器的分布
(b)表示训练辨别器,使得辨别器可以非常好地区分二者
©表示训练生成器,继续欺骗判别器
1.4 熵、交叉熵、KL散度、JS散度
熵(Entropy)
K-L散度源于信息论,常用的信息度量单位为熵(Entropy)
H=−∑i=1Np(xi)⋅logp(xi)H = -\sum_{i=1}^{N}p(x_i) \cdot logp(x_i)H=−i=1∑Np(xi)⋅logp(xi)
注意这个对数没有确定的底数(可以使2、e或者10)。
熵度量了数据的信息量,可以帮助我们了解用概率分布近似代替原始分布的时候我们到底损失了多少信息;但问题是如何将熵值压缩到最小值,即如何编码可以达到最小的熵(存储空间最优化)。
-
交叉熵: 量化两个概率分布之间的差异
H(p,q)=−∑xp(x)logq(x)H(p,q) = -\sum_{x}p(x) \; log \; q(x)H(p,q)=−x∑p(x)logq(x) -
KL散度(kullback-Leibler divergence):量化两种概率分布 P和Q之间差异的方式,又成为相对熵
将熵的定义公式稍加修改就可以得到K-L散度的定义公式:
DKL(P∣∣Q)=∑i=1Np(xi)⋅(logp(xi)−logq(xi))=∑i=1Np(xi)⋅logp(xi)q(xi)D_{KL}(P||Q) = \sum_{i=1}^{N} p(x_i) \cdot (log p(x_i) - log q(x_i)) = \sum_{i=1}^{N}p(x_i) \cdot log \frac{p(x_i)}{q(x_i)}DKL(P∣∣Q)=i=1∑Np(xi)⋅(logp(xi)−logq(xi))=i=1∑Np(xi)⋅logq(xi)p(xi)
其中ppp和qqq分别表示数据的原始分布和近似的概率分布。
根据公式所示,K-L散度其实是数据的原始分布p和近似分布之间的对数差的期望。如果用2位底数计算,K-L散度表示信息损失的二进制位数,下面用期望表示式展示:
DKL(P∣∣Q)=E[logp(x)−q(x)]D_{KL}(P||Q) = E[log p(x) - q(x)]DKL(P∣∣Q)=E[logp(x)−q(x)]
注意:
- 从散度的定义公式中可以看出其不符合对称性(距离度量应该满足对称性)
- KL散度非负性
JS散度(Jensen-shannon divergence)
由于K-L散度是非对称的,所以对其进行修改,使得其能够对称,称之为 JS散度
(1) 设 M=12(P+Q)M = \frac{1}{2}(P+Q)M=21(P+Q),则:
DJS(P∣∣Q)=12DKL(P∣∣M)+12DKL(Q∣∣M)D_{JS}(P||Q) = \frac{1}{2}D_{KL}(P||M) + \frac{1}{2}D_{KL}(Q||M)DJS(P∣∣Q)=21DKL(P∣∣M)+21DKL(Q∣∣M)
(2) 将KL散度公式带入上面
DJS=12∑i=1Np(xi)log(p(xi)p(xi)+q(xi)2)+12∑i=1Nq(xi)⋅log(q(xi)p(xi)+q(xi)2)D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{p(x_i)}{\frac{p(x_i) + q(x_i)}{2}}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{q(x_i)}{\frac{p(x_i)+q(x_i)}{2}})DJS=21i=1∑Np(xi)log(2p(xi)+q(xi)p(xi))+21i=1∑Nq(xi)⋅log(2p(xi)+q(xi)q(xi))
(3) 将logloglog中的12\frac{1}{2}21放到分子上
DJS=12∑i=1Np(xi)log(2p(xi)p(xi)+q(xi))+12∑i=1Nq(xi)⋅log(2q(xi)p(xi)+q(xi))D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{2p(x_i)}{p(x_i) + q(x_i)}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{2q(x_i)}{p(x_i)+q(x_i)})DJS=21i=1∑Np(xi)log(p(xi)+q(xi)2p(xi))+21i=1∑Nq(xi)⋅log(p(xi)+q(xi)2q(xi))
(4) 提出2
DJS=12∑i=1Np(xi)log(p(xi)p(xi)+q(xi))+12∑i=1Nq(xi)⋅log(q(xi)p(xi)+q(xi))+log(2)D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{p(x_i)}{p(x_i) + q(x_i)}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{q(x_i)}{p(x_i)+q(x_i)}) + log(2)DJS=21i=1∑Np(xi)log(p(xi)+q(xi)p(xi))+21i=1∑Nq(xi)⋅log(p(xi)+q(xi)q(xi))+log(2)
注意这里是因为∑p(x)=∑q(x)=1\sum p(x) = \sum q(x) = 1∑p(x)=∑q(x)=1
JS散度的缺陷:当两个分布完全不重叠的时候,几遍两个分布的中心离得很近,其JS散度都是一个常数,所以其获取的梯度是0,是没有办法进行更新的。而两个分布没有重叠的原因:从理论和经验而言,真实的数据分布其实是一个低维流形(不具备高维特征),而是存在一个嵌入在高维度的低维空间内。由于维度存在差异,数据很可能不存在分布的重合。
1.5 其他相关(正在补充!)
相关文章:

原始GAN-pytorch-生成MNIST数据集(原理)
文章目录1. GAN 《Generative Adversarial Nets》1.1 相关概念1.2 公式理解1.3 图片理解1.4 熵、交叉熵、KL散度、JS散度1.5 其他相关(正在补充!)1. GAN 《Generative Adversarial Nets》 Ian J. Goodfellow, Jean Pouget-Abadie, Yoshua Be…...

Vue下载安装步骤的详细教程(亲测有效) 1
目录 一、【准备工作】nodejs下载安装(npm环境) 1 下载安装nodejs 2 查看环境变量是否添加成功 3、验证是否安装成功 4、修改模块下载位置 (1)查看npm默认存放位置 (2)在 nodejs 安装目录下,创建 “node_global…...

[Android Studio] Android Studio生成数字证书,为应用签名
🟧🟨🟩🟦🟪 Android Debug🟧🟨🟩🟦🟪 Topic 发布安卓学习过程中遇到问题解决过程,希望我的解决方案可以对小伙伴们有帮助。 📋笔记目…...

应用IC 卡继续教育网络管理系统前后影响因素比较
3.1 实现了继续护理教育网络化管理近年来,随着一些医院继续护理教育管理信息系统的建立,有效改进了学分档案管理模式和教学模式,但这些继续护理教育管理信息系统一般为局域网,仅能达到满足自身管理的基本需求,而系统如…...
Clickhouse学习(一):MergeTree概述
MergeTree一、Clickhouse表引擎概述二、MergeTree表引擎<一>、ReplacingMergeTree引擎<二>、SummingMergeTree引擎<三>、AggregatingMergeTree引擎三、MergeTree分区一、Clickhouse表引擎概述 MergeTree表引擎:允许根据日期和主键创建索引 1、ReplacingMerge…...

Windows离线安装rust
目前rust安装常用的方式就是通过Rustup安装,此安装方式需要访问互联网。在生产环境中由于网络限制,不能直接访问互联网或者不能访问目标网站,这时候需要用离线安装的方式,本文将详细介绍离线安装步骤,并给出了vscode如…...
Android与flutter混合开发
这里我使用的android studio版本是2020.3.1;flutter版本2.5.3。此前在网上搜索的很多教教程版本都不一样,新版的IDE和SDK让我遇到了很多坑故这里整理一下。一、创建项目1.在Android项目中点击File->New->New Flutter Project。File->New->Ne…...

Linux和C语言的学习方法你真的知道吗?
★Linux的使用 第一天,就给我们讲了为什么要先学c、学linux:因为嵌入式的根本就是软件驱动硬件,而C语言是最接近硬件的语言、有指针的概念、可以直接操作硬件,另外,功能复杂的硬件是含有操作系统的,这就需…...

代码随想录day42
1049. 最后一块石头的重量 II https://leetcode.cn/problems/last-stone-weight-ii/ 这个自己还是没想出来01背包对应。 本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 stones [2,7,4,1,8,1]也就是sum…...

【笔记】两台1200PLC进行S7 通信(1)
使用两台1200系列PLC进行S7通信(入门) 文章目录 目录 文章目录 前言 一、通信 1.概念 2.PLC通信 1.串口 2.网口 …...

统一网关Gateway
为什么需要网关 网关功能: 身份认证和权限校验服务路由,负载均衡 根据请求判断找到对应的服务路由,然后服务可能有多个实例,这个时候网关就会做一个负载均衡去挑选一个实例调用.请求限流 限制请求的数量,这是微服务的…...
安装)
6、kubernetes(k8s)安装
本文内容以语雀为准 文档 等等,Docker 被 Kubernetes 弃用了?容器运行时端口和协议kubeadm initkubeadm config安装网络策略驱动使用 kubeadm 创建集群 控制平面节点隔离 持久卷为容器设置环境变量在CentOS上安装Docker引擎Pod 网络无法访问排查处理 说明 本文…...

python-批量下载某短视频平台音视频标题、评论、点赞数
python-批量下载某短视频平台音视频标题、评论数、点赞数前言一、获取单个视频信息1、获取视频 url2、发送请求3、数据解析二、批量获取数据1、批量导入地址2、批量导出excel文件3、批量存入mysql数据库三、完整代码前言 1、Cookie中文名称为小型文本文件,指某些网…...

【数据结构与算法】单链表的增删查改(附源码)
这么可爱的猫猫不值得点个赞吗😽😻 目录 一.链表的概念和结构 二.单链表的逻辑结构和物理结构 1.逻辑结构 2.物理结构 三.结构体的定义 四.增加 1.尾插 SListpushback 2.头插 SListpushfront 五.删除 1.尾删 SListpopback 2.头删 SListpo…...

华为OD机试 - 回文字符串
题目描述 如果一个字符串正读和反渎都一样(大小写敏感),则称它为一个「回文串」,例如: leVel是一个「回文串」,因为它的正读和反读都是leVel;同理a也是「回文串」art不是一个「回文串」,因为它的反读tra与正读不同Level不是一个「回文串」,因为它的反读leveL与正读不…...

C语言太简单?这14道C语言谜题,你能答对几个
14个C语言的迷题以及答案,代码应该是足够清楚的,而且有相当的一些例子可能是我们日常工作可能会见得到的。通过这些迷题,希望你能更了解C语言。 如果你不看答案,不知道是否有把握回答各个谜题?让我们来试试。 下面的…...
Benchmark测试——fio——源码分析
1. main 1.1 parse_options() 解析选项,更新数据结构 1.1.1 fio_init_options() 1.1.2 fio_test_cconv(&def_thread.o) <cconv.c> 1.1.2.1 convert_thread_options_to_cpu() 传递options给数据结构 1.1.3 parse_cmd_line() switch语句多路选择&am…...
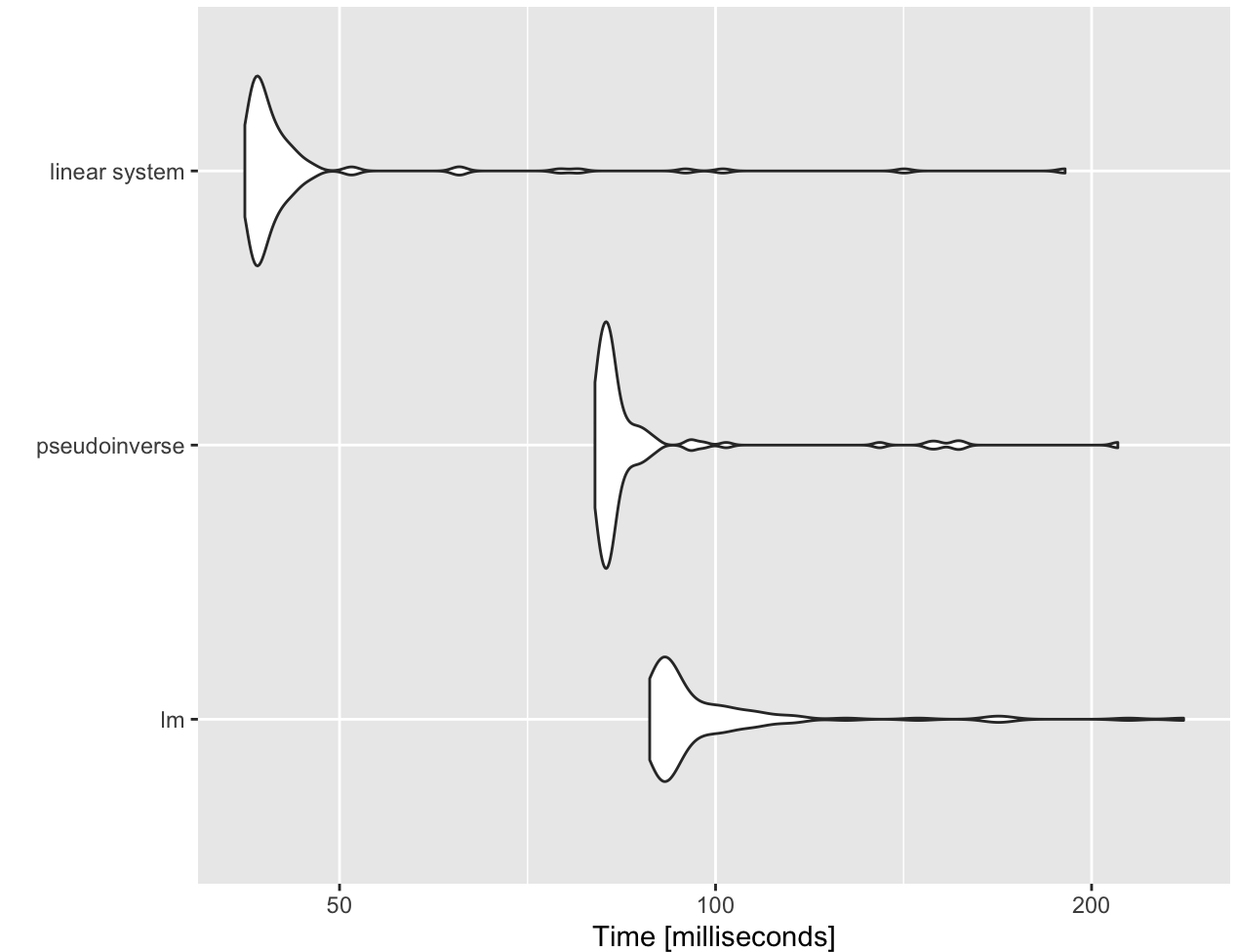
测量 R 代码运行时间的 5 种方法
简介 平常在撰写论文时,会需要比较算法之间的计算时间。本篇文章给出几种测量 R 代码运行时间的方法。本文是小编学习过程中的笔记,主要参考博客1,2。 1. 使用 Sys.time() 小编通常使用 Sys.time() 函数来计算时间。首先记录当前运行时刻&…...

Qt 第9课、计算器中缀转后缀算法
计算器核心算法: 1、将中缀表达式进行数字和运算符的分离 2、将中缀表达式转换成后缀表达式 3、通过后缀表达式计算最后的结果 二、计算器中缀转后缀算法 计算器中缀转后缀算法的意义在于把中缀表达式转换成后缀表达式,能够更好地计算 算法的基本思路…...
docker的使用方法
docker技术 同一个操作系统内跑多套不同版本依赖的业务 docker可以使同一个物理机中进程空间,网络空间,文件系统空间相互隔绝 虚拟机弊端:每个需要安装操作系统,太重量级,资源需要提前分配好 部署程序 开发环境 win…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
