k-means聚类总结
1.概述
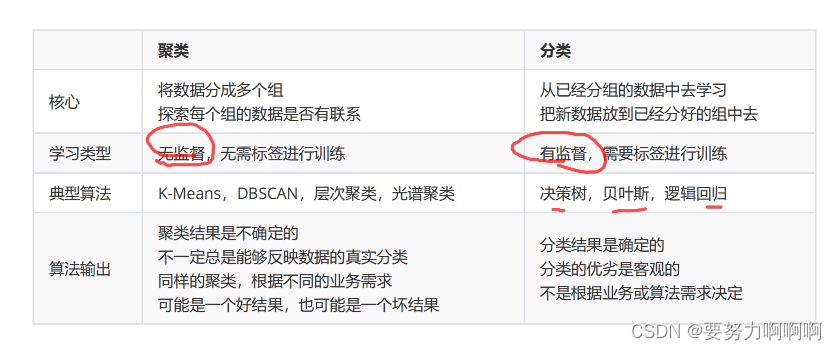
聚类算法又叫做‘无监督学习’,其目的是将数据划分成有意义或有用的组(或簇)。
2.KMeans
关键概念:簇与质心
KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
簇中所有数据的均值 通常被称为这个簇的“质心”(centroids)。在一个二维平面中,一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值,质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高
维空间。
3.簇内误差平方和的定义和解惑
我们认为,被分在同一个簇中的数据是有相似性的,而不同簇中的数据是不同的.因此我们追求“组内差异小,组间差异大”。聚类算法也是同样的目的,我们追求“簇内差异小,簇外差异大”。而这个“差异“,由样本点到其所在簇的质心的距离来衡量。对于一个簇来说,所有样本点到质心的距离之和越小,我们就认为这个簇中的样本越相似,簇内差异就越小。
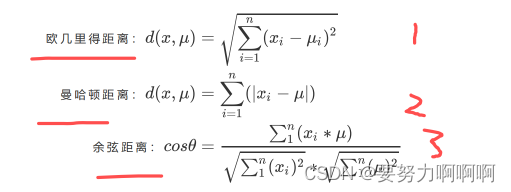
n代表每一个样本的特征个数,x代表样本,miu代表簇中的质心。

其中,m为一个簇中样本的个数,j是每个样本的编号。这个公式被称为簇内平方和(cluster Sum of Square),又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加,就得到了整体平方和(Total Cluster Sum of
Square),又叫做total inertia。Total Inertia越小,代表着每个簇内样本越相似,聚类的效果就越好。因此KMeans追求的是,求解能够让Inertia最小化的质心。
4.sklearn.cluster.KMeans
4.1重要参数n_clusters
n_clusters是KMeans中的k,表示着我们告诉模型我们要分几类。这是KMeans当中唯一一个必填的参数,默认为8类,但通常我们的聚类结果会是一个小于8的结果。
简单聚类
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt#首先简单的进行一次聚类
'''
步骤如下:
1。首先使用sklearn中的方法来自定义自己的数据
2。画出散点图,顺带画出已经分好簇的散点图,使用plot,同时也对原始的数据已经分好簇的数据进行画图描述使用四种颜色
3。基于这个分布,使用kmeans来进行聚类,需要导入聚类中的kmeans设置要分好的类别,然后对其进行拟合,预测的结果使用label可以看到预测出来的结果.使用sluster_centers_可以输出每一个簇的分类点的位置使用inertia_可以查看总的欧氏距离是多少
4。分别猜测其中有3,4,5,6四个簇,通过簇内平方和来判断哪一个数目是最好的。
'''#自己创建数据集,生成的数据大小是500*2,500个数据,每一个数据有两个特征,分别对应的是x1,x2
X,Y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)fig,ax1 = plt.subplots(1)
ax1.scatter(X[:,0],X[:,1],marker = 'o',s=8
)
color = ['red','pink','orange','gray']
# fig,ax2 = plt.subplots(1)
# for i in range(4):
# ax2.scatter(
# X[Y==i,0],
# X[Y==i,1],
# s=8,
# c=color[i]
# )
plt.show()from sklearn.cluster import KMeans
n_clusters = 3
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
n_clusters = 4
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
n_clusters = 5
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
n_clusters = 6
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
y_pred = cluster.labels_#聚类之后分好的类别。
print(y_pred)
pre = cluster.fit_predict(X)
#print(pre == y_pred)
inertia = cluster.inertia_
centroid = cluster.cluster_centers_
print(inertia)
color = ['red','pink','orange','gray','green','yellow']
fig , ax3 = plt.subplots()for i in range(n_clusters):ax3.scatter(X[y_pred==i,0],X[y_pred==i,1],marker='o',s=8,c=color[i])
ax3.scatter(centroid[:,0],centroid[:,1],marker='x',s=15,c='black')
plt.show()
4.2 聚类算法的模型评估指标
不同于分类模型和回归,聚类算法的模型评估不是一件简单的事。
1.在分类中,有直接结果(标签)的输出,并且分类的结果有正误之分,所以我们使用预测的准确度,混淆矩阵,ROC曲线等等指标来进行评估,但无论如何评估,都是在”模型找到正确答案“的能力。
2.回归中,由于要拟合数据,我们有SSE均方误差,有损失函数来衡量模型的拟合程度。但这些衡量指标都不能够使用于聚类。
4.3.1 当真实标签已知的时候
如果拥有真实标签,我们更倾向于使用分类算法。但不排除我们依然可能使用聚类算法的可能性。如果我们有样本真实聚类情况的数据,我们可以对于聚类算法的结果和真实结果来衡量聚类的效果。常用的有以下三种方法:
互信息分:取值范围在(0,1)之中越接近1;聚类效果越好;在随机均匀聚类下产生0分;
V-meature:取值范围在(0,1)之中越接近1;越接近1,聚类效果越好
调整兰德系数:取值范围在(0,1)之中越接近1;越接近1越好
4.3.2 当真实标签未知的时候:轮廓系数
其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的,它能够同时衡量:
1)样本与其自身所在的簇中的其他样本的相似度a,等于样本与同一簇中所有其他点之间的平均距离
2)样本与其他簇中的样本的相似度b,等于样本与下一个最近的簇中的所有点之间的平均距离
根据聚类的要求”簇内差异小,簇外差异大“,我们希望b永远大于a,并且大得越多越好。

很容易理解轮廓系数范围是(-1,1),其中值越接近1表示样本与自己所在的簇中的样本很相似,并且与其他簇中的样本不相似,当样本点与簇外的样本更相似的时候,轮廓系数就为负。当轮廓系数为0时,则代表两个簇中的样本相似度一致,两个簇本应该是一个簇。可以总结为轮廓系数越接近于1越好,负数则表示聚类效果非常差。
如果一个簇中的大多数样本具有比较高的轮廓系数,则簇会有较高的总轮廓系数,则整个数据集的平均轮廓系数越高,则聚类是合适的。如果许多样本点具有低轮廓系数甚至负值,则聚类是不合适的,聚类的超参数K可能设定得太大或者太小。
4.3.3 当真实标签未知的时候:Calinski-Harabaz Index
除了轮廓系数是最常用的,我们还有卡林斯基-哈拉巴斯指数(Calinski-Harabaz Index,简称CHI,也被称为方差比标准),戴维斯-布尔丁指数(Davies-Bouldin)以及权变矩阵(Contingency Matrix)可以使用。
在这里我们重点来了解一下卡林斯基-哈拉巴斯指数。Calinski-Harabaz指数越高越好。对于有k个簇的聚类而言,Calinski-Harabaz指数s(k)写作如下公式:
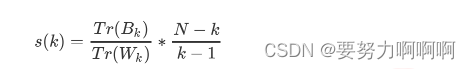
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from sklearn.datasets import make_blobs
n_clusters = 5
X,Y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)#是用来设置生成图片大小的
ax1.set_xlim([-0.1, 1])#设置x坐标轴的
ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])
clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
cluster_labels = clusterer.labels_#分出来的类别
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,"The average silhouette_score is :", silhouette_avg)
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]ith_cluster_silhouette_values.sort()#这里是为了能够从小到大向上排列size_cluster_i = ith_cluster_silhouette_values.shape[0]y_upper = y_lower + size_cluster_i#这里是留出来上下的空间color = cm.nipy_spectral(float(i)/n_clusters)#设置颜色使用的。'''进行颜色的填充。只不过是填充的方向不同。
fill_between是进行y轴方向上的填充,也就是竖直方向的填充
fill_betweenx是进行x轴方向上的填充,也就是水平方向的填充'''# 第一个参数是范围# 第二个参数表示填充的上界# 第三个参数表示填充的下界,默认0ax1.fill_betweenx(np.arange(y_lower, y_upper),ith_cluster_silhouette_values,facecolor=color,alpha=0.7)#进行颜色填充的ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))#精准的在图上的某一个点位进行写字。前面两个是坐标信息,后面是内容。y_lower = y_upper + 10
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")#ax1.axvline设置一条中轴线。所有样本的轮廓系数。
ax1.set_yticks([])
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1] ,marker='o',s=8,c=colors )
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers在簇中画出来质心
ax2.scatter(centers[:, 0], centers[:, 1], marker='x',
c="red", alpha=1, s=200)
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data ""with n_clusters = %d" % n_clusters), fontsize=14, fontweight='bold')
plt.show()
4.3 重要参数init & random_state & n_init:初始质心怎么放好?
在K-Means中有一个重要的环节,就是放置初始质心。如果有足够的时间,K-means一定会收敛,但Inertia可能收敛到局部最小值。是否能够收敛到真正的最小值很大程度上取决于质心的初始化。init就是用来帮助我们决定初始化方式的参数。
init:可输入"k-means++“,“random"或者一个n维数组。这是初始化质心的方法,默认"k-means++”。输入"kmeans++”:一种为K均值聚类选择初始聚类中心的聪明的办法,以加速收敛。
random_state:控制每次质心随机初始化的随机数种子
n_init:整数,默认10,使用不同的质心随机初始化的种子来运行k-means算法的次数。
4.4 重要参数max_iter & tol:让迭代停下来
当质心不再移动,Kmeans算法就会停下来。但在完全收敛之前,我们也可以使用max_iter,最大迭代次数,或者tol,两次迭代间Inertia下降的量,这两个参数来让迭代提前停下来。
max_iter:整数,默认300,单次运行的k-means算法的最大迭代次数
tol:浮点数,默认1e-4,两次迭代间Inertia下降的量,如果两次迭代之间Inertia下降的值小于tol所设定的值,迭
代就会停下
random = KMeans(n_clusters = 10,init="random",max_iter=10,random_state=420).fit(X)
y_pred_max10 = random.labels_
silhouette_score(X,y_pred_max10)
random = KMeans(n_clusters = 10,init="random",max_iter=20,random_state=420).fit(X)
y_pred_max20 = random.labels_
silhouette_score(X,y_pred_max20)
5.聚类算法用于降维,KMeans的矢量量化应用
相关文章:
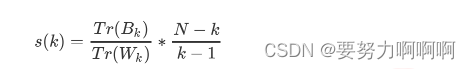
k-means聚类总结
1.概述 聚类算法又叫做‘无监督学习’,其目的是将数据划分成有意义或有用的组(或簇)。 2.KMeans 关键概念:簇与质心 KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的…...

char * 和const char *的区别
一、含义的不同 char* 表示一个指针变量,并且这个变量是可以被改变的。 const char*表示一个限定不会被改变的指针变量。 二、模式的不同 char*是常量指针,地址不可以改变,但是指针的值可变。 const char*是指向常量的常量指针ÿ…...

【剑指offer】JZ3 数组中重复的数字、 JZ4 二维数组中的查找
目录 JZ3 数组中重复的数字 思路: 解题步骤: JZ4 二维数组中的查找 思路 JZ3 数组中重复的数字 描述: 在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每…...

数据采集 - 笔记
1 redis GitHub - redis/redis: Redis is an in-memory database that persists on disk. The data model is key-value, but many different kind of values are supported: Strings, Lists, Sets, Sorted Sets, Hashes, Streams, HyperLogLogs, Bitmaps. Redis 通常被称为数…...

8年测开经验面试28K公司后,吐血整理出高频面试题和答案
#01、如何制定测试计划? ❶参考点 1.是否拥有测试计划的制定经验 2.是否具备合理安排测试的能力 3.是否具备文档输出的能力 ❷面试命中率 80% ❸参考答案 测试计划包括测试目标、测试范围、测试环境的说明、测试类型的说明(功能,安全&am…...

spring读取properties顺序,重复key问题
最近搞个开源工具,涉及到配置问题。 举例 有个应用A工具,打成jar给人用。应用B引用了A的jar A应用里resources/sys.properties文件里有个coreSize1 B引用了A,期望修改coreSize的值,改成2 开始天真以为,B应用里有同…...

什么是api接口?(基本介绍)
API:应用程序接口(API:Application Program Interface) 应用程序接口是一组定义、程序及协议的集合,通过 API 接口实现计算机软件之间的相互通信。API 的一个主要功能是提供通用功能集。程序员通过调用 API 函数对应用程序进行开发,可以减轻编程任务。 …...

【2023全网最全教程】从0到1开发自动化测试框架(建议收藏)
一、序言 随着项目版本的快速迭代、APP测试有以下几个特点: 首先,功能点多且细,测试工作量大,容易遗漏;其次,代码模块常改动,回归测试很频繁,测试重复低效;最后&#x…...

3-5天炒股短线战法指标思想结合----超级短线源码无未来
超级短线以3-5个交易日获利3-5个点为目标,经过长期总结、实践、实盘操作编写的一个短线指标和思想! 如果你认为这一个指标像股市提款机一个,可以随意的赚钱,请你不要购买; 如果你你购买了指标又不想思考分析,想随意的赚…...

原始GAN-pytorch-生成MNIST数据集(代码)
文章目录原始GAN生成MNIST数据集1. Data loading and preparing2. Dataset and Model parameter3. Result save path4. Model define6. Training7. predict原始GAN生成MNIST数据集 原理很简单,可以参考原理部分原始GAN-pytorch-生成MNIST数据集(原理&am…...

注意,这些地区已发布2023年上半年软考报名时间
距离2023年上半年软考报名越来越近了,目前已有山西、四川、山东等地区发布报名简章,其中四川3月13日、山西3月14日、山东3月17日开始报名。 四川 报名时间:3月13日至4月3日。 2.报名入口:https://www.ruankao.org.cn/ 缴费时间…...

Html引入外部css <link>标签 @import
Html引入外部css 方法1: <link rel"stylesheet" href"x.css"> <link rel"stylesheet" href"x.css" /><link rel"stylesheet" href"x.css" type"text/css" /><link rel"sty…...

React源码分析8-状态更新的优先级机制
这是我的剖析 React 源码的第二篇文章,如果你没有阅读过之前的文章,请务必先阅读一下 第一篇文章 中提到的一些注意事项,能帮助你更好地阅读源码。 文章相关资料 React 16.8.6 源码中文注释,这个链接是文章的核心,文…...

如何在ChatGPT的API中支持多轮对话
一、问题 ChatGPT的API支持多轮对话。可以使用API将用户的输入发送到ChatGPT模型中,然后将模型生成的响应返回给用户,从而实现多轮对话。可以在每个轮次中保留用户之前的输入和模型生成的响应,以便将其传递给下一轮对话。这种方式可以实现更…...

华为OD机试模拟题 用 C++ 实现 - 猜字谜(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明猜字谜题目输入输出描述备注示例一输入输出示例二输入输出思路Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,...

Containerd容器运行时将会替换Docker?
文章目录一、什么是Containerd?二、Containerd有哪些功能?三、Containerd与Docker的区别四、Containerd是否会替换Docker?五、Containerd安装、部署和使用公众号: MCNU云原生,欢迎微信搜索关注,更多干货&am…...

java虚拟机中对象创建过程
java虚拟机中对象创建过程 我们平常创建一个对象,仅仅只是使用new关键字new一个对象,这样一个对象就被创建了,但是在我们使用new关键字创建对象的时候,在java虚拟机中一个对象是如何从无到有被创建的呢,我们接下来就来…...

3485. 最大异或和
Powered by:NEFU AB-IN Link 文章目录3485. 最大异或和题意思路代码3485. 最大异或和 题意 给定一个非负整数数列 a,初始长度为 N。 请在所有长度不超过 M的连续子数组中,找出子数组异或和的最大值。 子数组的异或和即为子数组中所有元素按位异或得到的…...
SpringBoot:SpringBoot配置文件.properties、.yml 和 .ymal(2)
SpringBoot配置文件1. 配置文件格式1.1 application.properties配置文件1.2 application.yml配置文件1.3 application.yaml配置文件1.4 三种配置文件优先级和区别2. yaml格式2.1 语法规则2.2 yaml书写2.2.1 字面量:单个的、不可拆分的值2.2.2 数组:一组按…...

QT 学习之QPA
QT 为实现支持多平台,实现如下类虚函数 Class Overview QPlatformIntegration QAbstractEventDispatcherQPlatformAccessibilityQPlatformBackingStoreQPlatformClipboardQPlatformCursorQPlatformDragQPlatformFontDatabaseQPlatformGraphicsBufferQPlatformInput…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
