ICA简介:独立成分分析
1. 简介
您是否曾经遇到过这样一种情况:您试图分析一个复杂且高度相关的数据集,却对信息量感到不知所措?这就是独立成分分析 (ICA) 的用武之地。ICA 是数据分析领域的一项强大技术,可让您分离和识别多元数据集中的底层独立来源。
ICA 之所以重要,是因为它提供了一种理解数据集隐藏结构的方法,可用于各种应用,例如信号处理、脑成像、金融和许多其他领域。此外,ICA 可以帮助从数据中提取最相关的信息,提供有价值的见解,否则这些见解将在大量相关性中丢失。
在本文[1]中,我们将深入探讨ICA 的基础知识,ICA 算法,以及如何在数据分析项目中实施它。
2. 主要思想
独立成分分析是各种无监督学习算法中的一种,这意味着我们在使用模型之前不需要对其进行监督。这种方法的起源来自信号处理,我们试图将多变量信号分离成加性子分量。让我们进入对主要思想的解释:
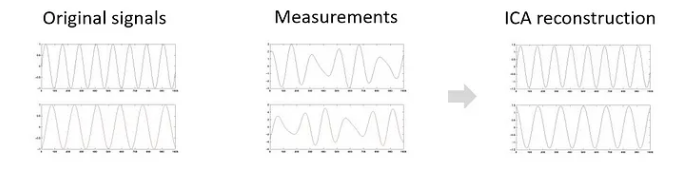
想象一些独立的信号或变量。这些信号可以表示为信号曲线,在上图中,第一个信号位于顶部,第二个信号位于底部。作为测量的结果,我们没有收到包含信号本身的数据集,而是包含这两个信号的测量值的数据集,不幸的是,这两个信号被混合成不同的线性组合。 ICA 的目标是通过分离混合数据来恢复原始的未知信号。最终目的是重建数据,使每个维度相互独立。
为了使这个概念更具体,将使用 ICA 最著名的例子,即“鸡尾酒会问题”。
2.1. 鸡尾酒会问题
想象一下,参加一个多人同时发言的鸡尾酒会,很难听懂一个人的谈话。值得注意的是,在这种情况下,人类具有分离个人语音流的能力。从技术上讲,这变得有点具有挑战性。

假设我们使用两个麦克风记录聚会中两组的对话。这会导致两个混合信号,其中第一次测量对第一组的影响较大,对第二组的影响较小,而第二次测量对第二组的影响较大。

这个的一般框架可以在灰色框中用矢量符号表示。矢量 X 中的测量实际上是矢量 S 的信号乘以一些混合系数,在矩阵 A 中表示。由于我们想要提取完整的对话(原始信号),我们需要为矢量 S 解决这个问题。

2.2. ICA vs. PCA
您可能已经猜到 ICA 在某种程度上与主成分分析 (PCA) 相关。这个假设并没有错。这两个概念背后的想法相差不大,但它们在最后阶段有所不同,我们将在后面看到。
让我们总结一下 PCA 的基本作用:假设我们有两个看起来相关的变量。通过使用这些变量的特征向量和特征值最大化方差,我们可以将它们转换为主成分。在此特定示例中,PCA 很好地识别了此关系的主要方向。
让我们以前面的鸡尾酒示例为例。在一个非常简单的表示中,我们可以想象来自麦克风 1 和 2 的两个测量值具有形成类似交叉模式的关系。如果我们在这种情况下应用 PCA,我们会得到错误的结果,因为 PCA 无法处理具有多个主要方向的数据集。
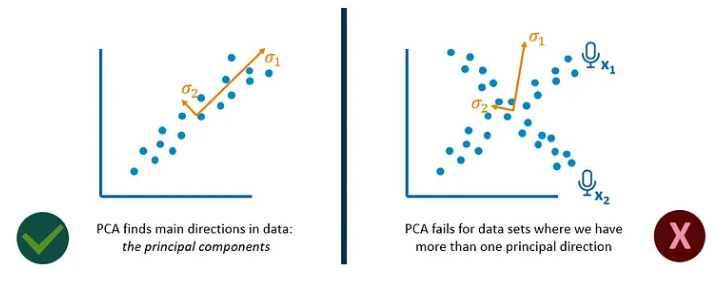
另一方面,ICA 通过关注独立成分而不是主要成分来解决这个问题。
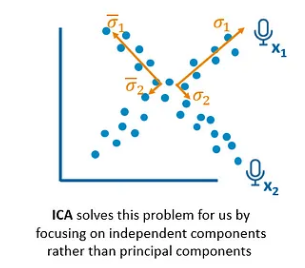
重要的是要回顾既定的概念框架。从麦克风获得的读数对应于已乘以混合矩阵 A 的原始信号。通过关于向量 S 重新排列方程,确定原始变量的唯一必要信息是矩阵 A。然而,矩阵 A 是未知的.

因此,要全面了解矩阵A并最终计算出向量S,需要通过一系列步骤进行逆运算。这些连续的逆运算构成了 ICA 算法的三个阶段,现在将对其进行更详细的分析。
3. ICA 算法
在进行 R 中的实际演示之前,了解算法的三个步骤很重要。该算法的目标是执行向量 X 与矩阵 A 的乘法。矩阵 A 由三个组成部分组成,它们是不同因素之间相乘相互作用的结果:
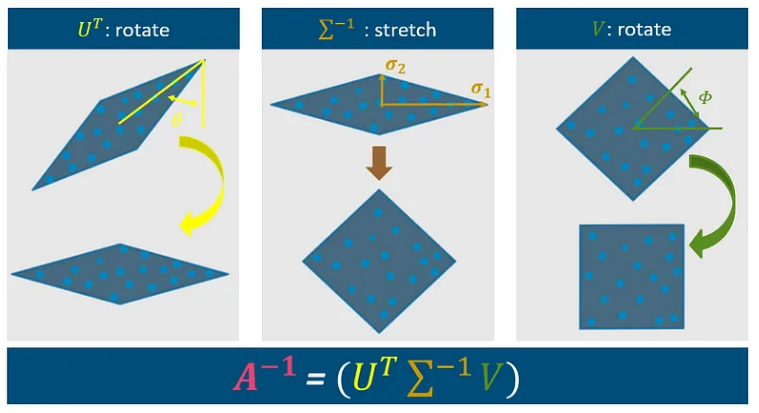
3.1. Step 1
找到具有最大方差的角度来旋转 |估计 U^T
该算法的第一个组成部分涉及使用基于第一个角度 Theta 的矩阵 U^T。角度 Theta 可以从数据的主要方向导出,如通过主成分分析 (PCA) 确定的那样。此步骤将图形旋转到如上所示的位置。
3.2. Step 2
找到主成分的比例 |估计 ∑^(-1)
第二个组成部分涉及拉伸图形,这是通过 Sigma^-1 步骤实现的。此步骤使用数据中的 sigma 1 和 sigma 2 的方差,类似于 PCA 中使用的方法。
3.3. Step 3
旋转的独立性和峰度假设 |估计 V
将当前算法与 PCA 区分开来的最后一个组成部分涉及信号围绕角度 Phi 的旋转。此步骤旨在通过利用旋转的独立性和峰度假设来重建信号的原始维度。
总之,该算法采用测量并围绕 theta 执行旋转,通过使用方差 sigma 1 和 2 进行拉伸,最后围绕 Phi 旋转。以下幻灯片总结了这些步骤的数学背景以供参考。
如您所见,我们可以仅使用两个角度和数据的方差来确定逆矩阵 A,这实际上是我们处理 ICA 算法所需的全部。进行测量、旋转和缩放它们。最后,我们再次旋转它们以获得最终尺寸。
4. 代码
我希望你到目前为止已经理解了 ICA 算法的基本思想。没有必要从数学上理解每一步,但有助于理解其背后的概念。有了这些知识,我想和你一起做一个实际的例子来展示 ICA 算法的实际应用,使用 R 中一个叫做 fastICA 的函数。
# install fastICA package in R
install.packages("fastICA")
# load required libraries
library(MASS) # To use mvrnorm()
library(fastICA)
我们创建了两个随机数据集:信号 1 和信号 2,可以将其想象为来自我们两个鸡尾酒组的语音信号:
# random data for signal 1
s1=as.numeric(0.7*sin((1:1000)/19+0.57*pi) + mvrnorm(n = 1000, mu = 0, Sigma = 0.004))
plot(s1, col="red", main = "Signal 1", xlab = "Time", ylab = "Amplitude")
# random data for signal 1
s2=as.numeric(sin((1:1000)/33) + mvrnorm(n = 1000, mu = 0.03, Sigma = 0.005))
plot(s2, col="blue", main = "Signal 2",xlab = "Time", ylab = "Amplitude")
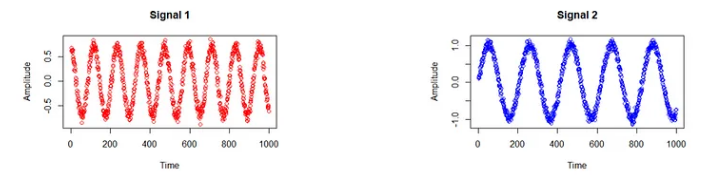
红色曲线代表第一个信号,蓝色曲线代表第二个信号。在这种情况下,形状无关紧要。您应该看到的是这两个信号彼此不同。现在让我们混合它们!
# measurements with mixed data x1 and x2
x1 <- sine1-2*sine2
plot(x1, main = "Linearly Mixed Signal 1", xlab = "Time", ylab = "Amplitude")
x2 <- 1.73*sine1 +3.41*sine2
plot(x2, main = "Linearly Mixed Signal 2", xlab = "Time", ylab = "Amplitude")
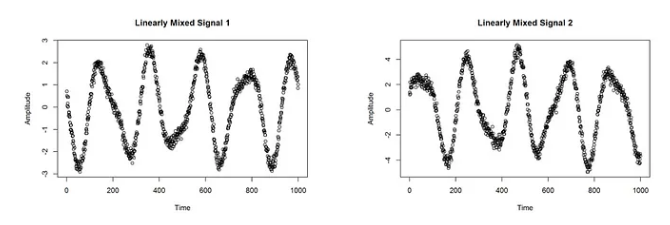
正如您在上面看到的,我们使用两个信号模拟了两个测量。因此,测量中的信号不再独立。两种混合信号都可以想象成鸡尾酒示例中两个麦克风的录音。我们现在忘记我们的两个原始信号并想象,这两个测量值是我们拥有的关于该数据的唯一信息。
因此我们想将它们分开,最终得到两个独立的信号:
# apply fastICA function to identify independent signals
measurements <- t(rbind(x1,x2))
estimation <- fastICA(measurements, 2, alg.typ = "parallel", fun = "logcosh", alpha = 1, method = "C", row.norm = FALSE, maxit = 200, tol = 0.0001, verbose = TRUE)
plot(estimation$S[,1], col="red", main = "Estimated signals", xlab = "Time", ylab = "Amplitude")
lines(estimation$S[,2], col="blue")
mtext("Signal 1 estimation in red, Signal 2 estimation in blue")
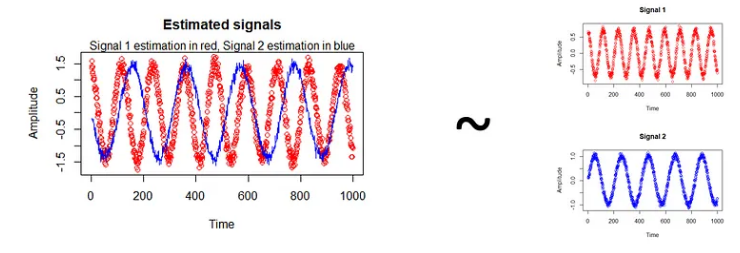
该算法的结果如上所示。红色曲线是信号 1 的估计值,而蓝色曲线是信号 2 的估计值。毫不奇怪,该算法几乎估计了原始信号,如右图所示。您可能已经注意到,红色曲线与预期完全吻合,而蓝色曲线似乎是倒转的。这是因为该算法无法恢复源活动的确切幅度。但除此之外,这里的重建工作做得非常好。
总结
优点
ICA 只能分离线性混合源,而且我们无法完美分离高斯分布的源,因为它们会终止我们算法的第三步。虽然我们期望独立源混合在线性组合中,但 ICA 会找到一个空间,即使是非独立源也能最大限度地独立。
缺点
ICA 算法是一种适用于不同领域的强大方法,并且很容易在 R 的开源包中使用; Mathlab 和其他系统。 ICA 算法用于应用程序的示例有很多:人脸识别应用程序、股票市场预测等等。因此,它在实际使用中是一种重要且备受推崇的方法。
参考资料
Source: https://towardsdatascience.com/introduction-to-ica-independent-component-analysis-b2c3c4720cd9
本文由 mdnice 多平台发布
相关文章:

ICA简介:独立成分分析
1. 简介 您是否曾经遇到过这样一种情况:您试图分析一个复杂且高度相关的数据集,却对信息量感到不知所措?这就是独立成分分析 (ICA) 的用武之地。ICA 是数据分析领域的一项强大技术,可让您分离和识别多元数据集中的底层独立来源。 …...

②【Java 组】蓝桥杯省赛真题解析 [振兴中华] [三部排序] 持续更新中...
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 蓝桥杯真题--持续更新中...一、振兴中华二、三…...

PostgreSql 视图
一、概述 视图(View)本质上是一个存储在数据库中的查询语句。视图本身不包含数据,也被称为虚拟表。 我们在创建视图时给它指定了一个名称,然后可以像表一样对其进行查询。 优势: 不保存数据,节省空间。减少…...
)
【PAT甲级题解记录】1150 Travelling Salesman Problem (25 分)
【PAT甲级题解记录】1150 Travelling Salesman Problem (25 分) 前言 Problem:1150 Travelling Salesman Problem (25 分) Tags:模拟 图的遍历 旅行商问题 Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1150 Travell…...
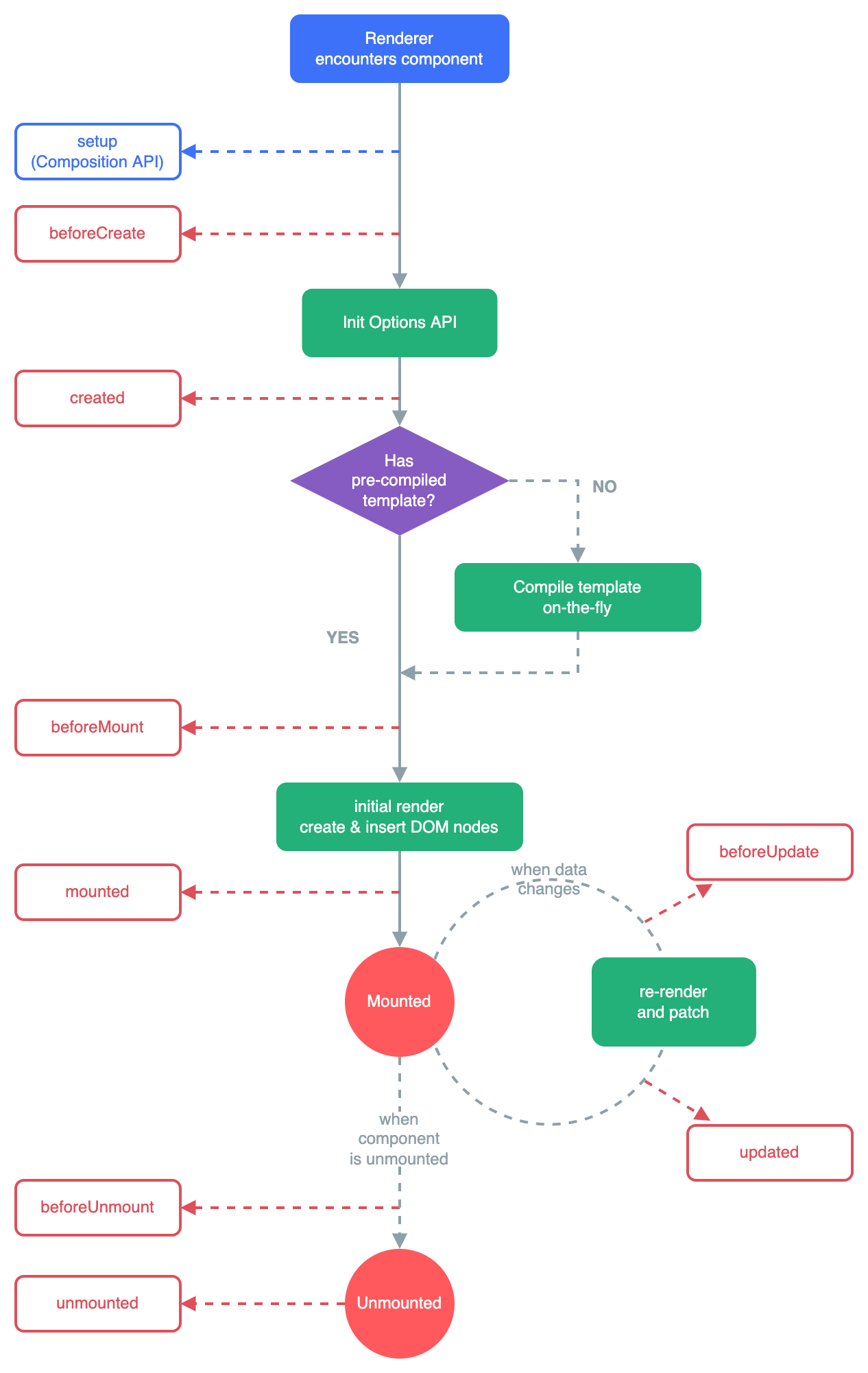
vue生命周期
vue生命周期是什么?Vue生命周期是指vue实例对象从创建之初到销毁的过程,vue所有功能的实现都是围绕其生命周期进行的,在生命周期的不同阶段调用对应的钩子函数可以实现组件数据管理和DOM渲染两大重要功能。我们来看一下官网给的vue生命周期的…...

排查解决Java进程占用内存过高
排查解决Java进程占用内存过高1 在项目部署运行之前1 检查JVM参数设置2 检查代码逻辑3 使用内存分析工具4 检查线程5 调整应用程序的设计7 调整硬件资源2 在项目部署运行之后1 在项目部署运行之前 1 检查JVM参数设置 检查JVM的启动参数设置,包括-Xmx和-Xms参数&am…...
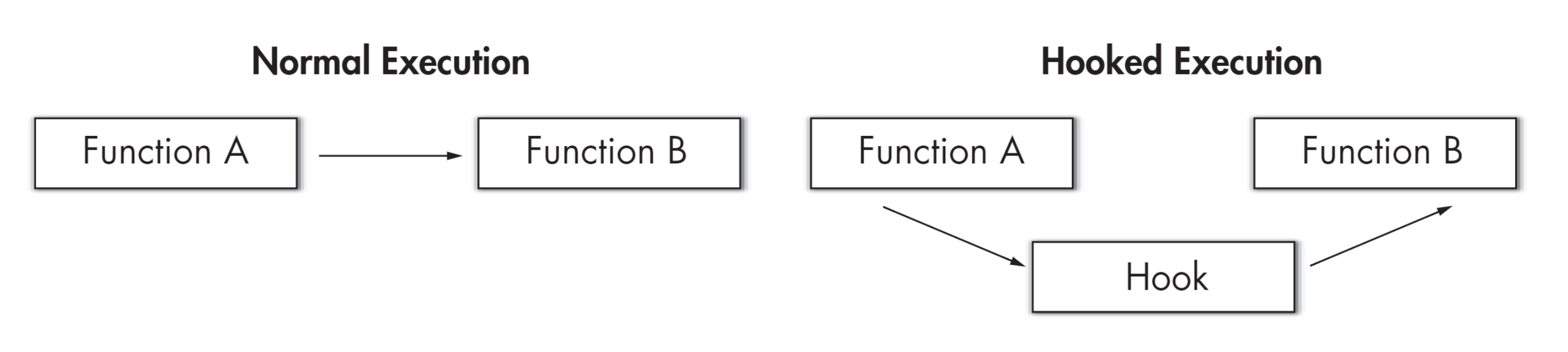
一个基于 LKM 的 Linux 内核级 rootkit 的实现
博客已迁移至:https://gls.show/ GitHub链接 演示Slides overview rootkit是一种恶意软件,攻击者可以在获得 root 或管理员权限后安装它,从而隐藏入侵并保持root权限访问。rootkit可以是用户级的,也可以是内核级的。关于rootk…...

CAN工具 - ValueCAN - 基础介绍(续)
VSpy3(Vehicle Spy 3的简写),作为一个常用的车载总线仿真工具,在车载网络领域也是有非常大的市场,前面也简单介绍过一些简单的功能,今天就再次介绍一些。什么是VSpy3?VSpy3是美国英特佩斯公司下…...
一个Laravel+vue免费开源的基于RABC控制的博客系统
项目介绍 CCENOTE 是一个使用 Vue3 Laravel8 开发的前后端分离的基于RABC权限控制管理的内容管理系统,由于作者本人比较喜欢写作的原因,因此开发了这个项目,后端使用的PHP的Laravel框架,并且整理了数据层与业务层,相…...
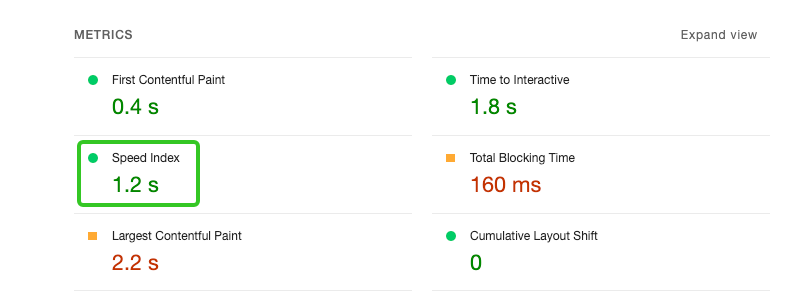
从 B 站出发,用 Chrome devTools performance 分析页面如何渲染
页面是如何渲染的?通常会得到“解析 HTML、css 合成 Render Tree,就可以渲染了”的回答。但是具体都做了些什么,却很少有人细说,我们今天就从 Chrome 的性能工具开始,具体看看一个页面是如何进行渲染的,以及…...
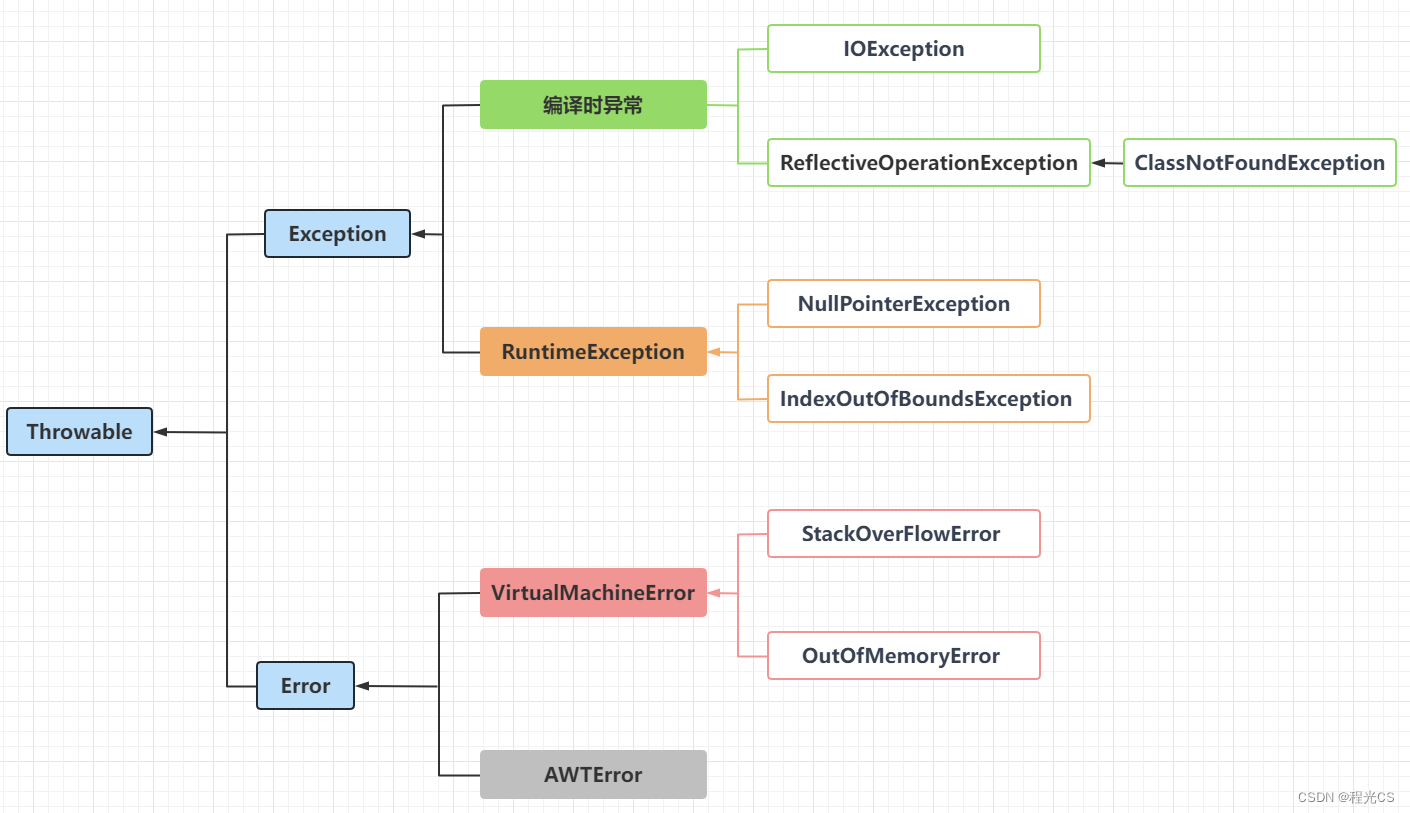
Java异常Throwable的分类
1. Exception:程序本身可以捕获并且可以处理的异常 编译时异常:编译期就会检查的异常,若调用的方法中throw了此类异常,则必须进行显式处理处理(用try…catch捕获或者throws向上抛出),否则无法通…...

【mybatis的#和$使用和区别】
MyBatis是一种基于Java的持久层框架,用于将数据库操作和Java对象之间的映射进行处理。在MyBatis中,#和 $ 符号是用于SQL语句中的占位符。 在SQL语句中,#和 $ 符号都表示占位符,但它们的使用方式略有不同: # 符号 #符…...

感知趋势,洞察发展:2023(第十届)趋势与预测大会成功举办
2023年2月23日,运联年会:2023(第十届)趋势与预测大会在深圳机场凯悦酒店成功闭幕。自2014年开始,“运联年会:趋势与预测”已经连续举办九届。这场大会,既是一次行业性的“年终总结”,…...

Spring-Aop核心技术
前言spring一直以来都是我们Java开发中最核心的一个技术,其中又以ioc和aop为主要技术,本篇文章主要讲一下aop的核心技术,也就是ProxyFactory技术的使用,而基本的jdk动态代理和cglib代理技术并不涉及,如有需要ÿ…...

webpack常用优化原理剖析
webpack常用优化原理剖析 按需加载代码配置原理CDN加速-externals代码配置GZIP压缩代码配置原理Tree Shaking代码配置原理按需加载 把不同路由对应的组件分割成不同的代码块,然后当路由被访问的时候才加载对应组件. 代码配置 //定义了一个异步函数,由于函数不调用不执行,所…...

【现在努力还不晚】--MySQL数据库的数据模型
目录 1、关系型数据库(RDBMS) 特点 2、数据模型 在学习MySQL之前要了解一下数据库的数据模型,我们就知道在MySQL当中,数据是如何存储的,我们了解一下概念! 1、关系型数据库(RDBMS࿰…...
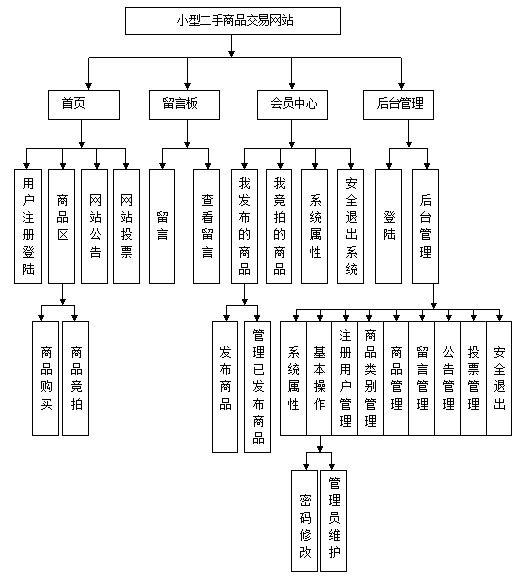
二手商品交易网站
技术:Java、JSP等摘要:随着科学技术和信息通讯的飞速发展,Internet极大地丰富和改变着我们生活的各个行业。随着Internet的普及应用,人们可以跨越时间和空间的限制,足不出户便能通过网络完成信息交流,而完成…...
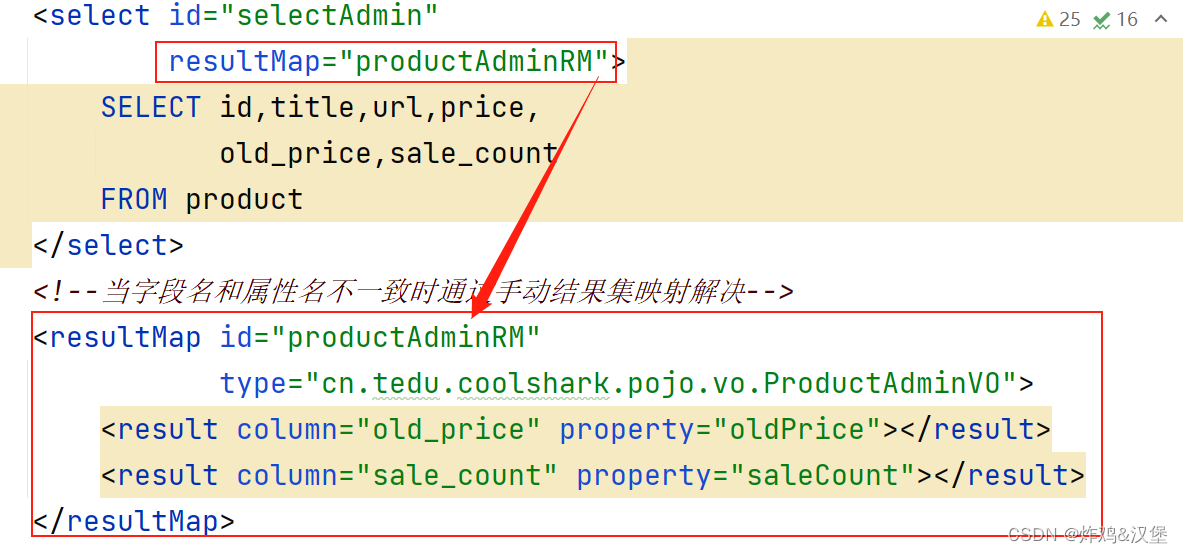
第三阶段04-同步请求和异步请求,get/post,Josn,pojo,Session/Cookie,过滤器Filter
文章目录同步请求和异步请求客户端如何发出异步请求自定义模板代码Get和Post请求异步版本的注册和登录商品管理系统(异步版本)商品列表步骤:前后端分离为什么需要前后端分离?为什么以后不再使用同步请求?JSONPOJO会话对象Session如何记住登录状态后端的MVC会话管理Cookie通过…...

Spark学习:spark相似算子解析
spark算子 一、Map、Flatmap和MapPartition二、repartition和coalesce三、reduceByKey和groupByKey四、collect、take和first一、Map、Flatmap和MapPartition 算子作用map接收一个高阶函数f,对每个算子进行f操作flatmap接收一个高阶函数f,对每个元素进行f操作,形成一个大的集合…...
)
MySQL操作数据表-----------创建数据表(一)
在MySQL中创建数据库完成后,需要使用USE 数据库名的形式指定进行操作的数据库,然后再去执行创建数据表的SQL语句,也可以直接使用数据库名.数据表名的形式创建数据表。 1.创建空数据表 语法格式:CREATE TABLE [IF EXISTS] 表名 &…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
