Codeforces Round #851 (Div. 2)(A~D)
A. One and Two

给出一个数组,该数组仅由1和2组成,问是否有最小的k使得k位置的前缀积和后缀积相等。
思路:计算2个数的前缀和即可,遍历判断。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 1e5 + 5;
int t, n;
int a[N], pre[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n;for(int i = 1; i <= n; i ++) {std::cin >> a[i];if(a[i] == 2)pre[i] = pre[i - 1] + 1;elsepre[i] = pre[i - 1];}int ans = -1;for(int i = 1; i <= n; i ++) {if(pre[i] == pre[n] - pre[i]) {ans = i;break;}}std::cout << ans << '\n';}return 0;
}B. Sum of Two Numbers

给出一个数字n,求x和y,满足x+y=n,x和y的各位数之和相差不超过1。
思路:直接对于每一位均分即可。如果该位为奇数,1的个数交替给x和y。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 1e5 + 5;
int t, n;
bool vis[15];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n;char a[15] = {0}, b[15] = {0}, cnta = 0, cntb = 0;memset(vis, 0, sizeof(vis));std::string s = std::to_string(n);for(int i = 0; i < s.length(); i ++) {int num = s[i] - '0';if(!(num & 1))a[cnta ++] = num / 2 + '0', b[cntb ++] = num / 2 + '0';else {vis[cnta] = 1;a[cnta ++] = num / 2 + '0', b[cntb ++] = num / 2 + '0';}}int pos = 0;for(int i = 0; i <= 15; i ++) {if(vis[i]) {if(pos)a[i] = a[i] - '0' + 1 + '0';elseb[i] = b[i] - '0' + 1 + '0';pos ^= 1;}}int x = std::atoi(a), y = std::atoi(b);std::cout << x << ' ' << y << '\n';}return 0;
}os:这个代码写的像shit一样。。。
C. Matching Numbers

给出1~2*n这些数,能否分成两两一组,使得每组的和是连续的数?
思路:很显然,n为偶数时,是不可以按要求分组的。n为奇数时,手摸几组样例可以知道,这个连续的数字是1+2*n-n/2 ~ 1+2*n+n/2,然后从大数开始,发现后n/2个数可以表示后n/2个和,下面n/2个数可以表示前n/2个和。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
typedef std::pair<int, int> PII;
const int N = 2e5 + 5;
int t, n;
bool vis[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n;if(!(n & 1)) {std::cout << "NO" << '\n';continue;}std::vector<PII> vec;vec.push_back({n, n + 1});int num = 2 + 2 * n;for(int i = n * 2; i >= 2 * n - n / 2 + 1; i --) {vec.push_back({i, num - i});num ++;}num = 1 + 2 * n - n / 2;for(int i = 2 * n - n / 2; i >= n + 2; i --) {vec.push_back({i, num - i});num ++;}std::cout << "YES" << '\n';for(auto [x, y] : vec)std::cout << x << ' ' << y << '\n';}return 0;
}D. Moving Dots

在一个数轴上有n个数,每个点都以相同的速度移动,若是左右两点的距离不同,向距离较小的点移动;若是相同,则向左移动。两个点移动到一起时,他们会停下。对于每个子序列,问剩下的点的和是多少。
思路:每一对点,它会有贡献的时候是他们两个向中间相向而行,最后汇聚成一个点。那么我们可以计算每一对点的贡献,在一个字序列中,这对点有贡献的时候是他们两个两侧没有相距更小而使得这一对点向背而行,其他的点任选即可,即2^n中选择方法。
学习大佬的思路
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 3e3 + 5;
const int mod = 1e9 + 7;
int n;
int a[N];template<const int T>
struct ModInt {const static int mod = T;int x;ModInt(int x = 0) : x(x % mod) {}ModInt(ll x) : x(int(x % mod)) {} int val() { return x; }ModInt operator + (const ModInt &a) const { int x0 = x + a.x; return ModInt(x0 < mod ? x0 : x0 - mod); }ModInt operator - (const ModInt &a) const { int x0 = x - a.x; return ModInt(x0 < 0 ? x0 + mod : x0); }ModInt operator * (const ModInt &a) const { return ModInt(1LL * x * a.x % mod); }ModInt operator / (const ModInt &a) const { return *this * a.inv(); }void operator += (const ModInt &a) { x += a.x; if (x >= mod) x -= mod; }void operator -= (const ModInt &a) { x -= a.x; if (x < 0) x += mod; }void operator *= (const ModInt &a) { x = 1LL * x * a.x % mod; }void operator /= (const ModInt &a) { *this = *this / a; }friend std::ostream &operator<<(std::ostream &os, const ModInt &a) { return os << a.x;}ModInt pow(int64_t n) const {ModInt res(1), mul(x);while(n){if (n & 1) res *= mul;mul *= mul;n >>= 1;}return res;}ModInt inv() const {int a = x, b = mod, u = 1, v = 0;while (b) {int t = a / b;a -= t * b; std::swap(a, b);u -= t * v; std::swap(u, v);}if (u < 0) u += mod;return u;}};
typedef ModInt<1000000007> mint;mint pow2[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> n;pow2[0] = 1;for(int i = 1; i <= n; i ++) {std::cin >> a[i];pow2[i] = pow2[i - 1] * 2;}mint ans = 0;for(int i = 1; i <= n; i ++) {for(int j = i + 1; j <= n; j ++) {int d = a[j] - a[i];int l = std::lower_bound(a + 1, a + 1 + n, a[i] - d) - a - 1;int r = std::lower_bound(a + 1, a + 1 + n, a[j] + d) - a;ans += pow2[l + n - r + 1];}}std::cout << ans << '\n';return 0;
}相关文章:

Codeforces Round #851 (Div. 2)(A~D)
A. One and Two给出一个数组,该数组仅由1和2组成,问是否有最小的k使得k位置的前缀积和后缀积相等。思路:计算2个数的前缀和即可,遍历判断。AC Code:#include <bits/stdc.h>typedef long long ll; const int N 1…...

内存保护_1:Tricore芯片MPU模块介绍
上一篇 | 返回主目录 | 下一篇 内存保护_1:Tricore芯片MPU模块介绍1 何为MPU2 MPU相关的硬件子系统2.1 基于地址范围保护逻辑说明2.1.1 地址范围寄存器2.1.2 读、写、执行权限寄存器2.1.3 保护集设置位2.1.4 内存保护功能使能位2.1.5 核的内存保护范围获取说明2.1.6…...

Vue3 -- PDF展示、添加签名(带笔锋)、导出
文章目录笔锋签名方案一实现要点实现过程组件引用页面元素添加引用实现代码效果展示缺点方案二修改页面元素替换引用修改代码效果展示完整代码地址实现功能的时候采用了两个方案,主要是第一个方案最后的实现效果并不太理想,但实现起来比较简单࿰…...
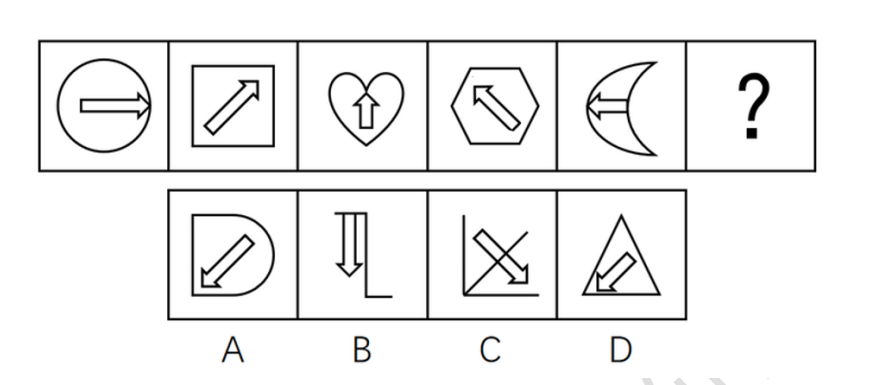
行测-判断推理-图形推理-样式规律-属性规律-曲直性
左边的图全是由曲线构成的选C1 3 5全是由曲线构成的2 4 6全是由直线构成的第三行的图形有曲有直选A1 3 5有曲有直2 4 6全是直线选D图形有曲有直,排除B D外曲内直->内曲外直->外曲内直->内曲外直->外曲内直->内曲外直所以问号出的图形应该是内曲外直选…...

idea集成Alibaba Cloud Toolkit插件
idea集成Alibaba Cloud Toolkit插件 使用该插件主要是简化打包、上传、启动服务的相关操作。 很早之前的方式是使用开发工具(eclipse,idea),使用maven命令完成项目打包(这里指jar),然后通过shell工…...
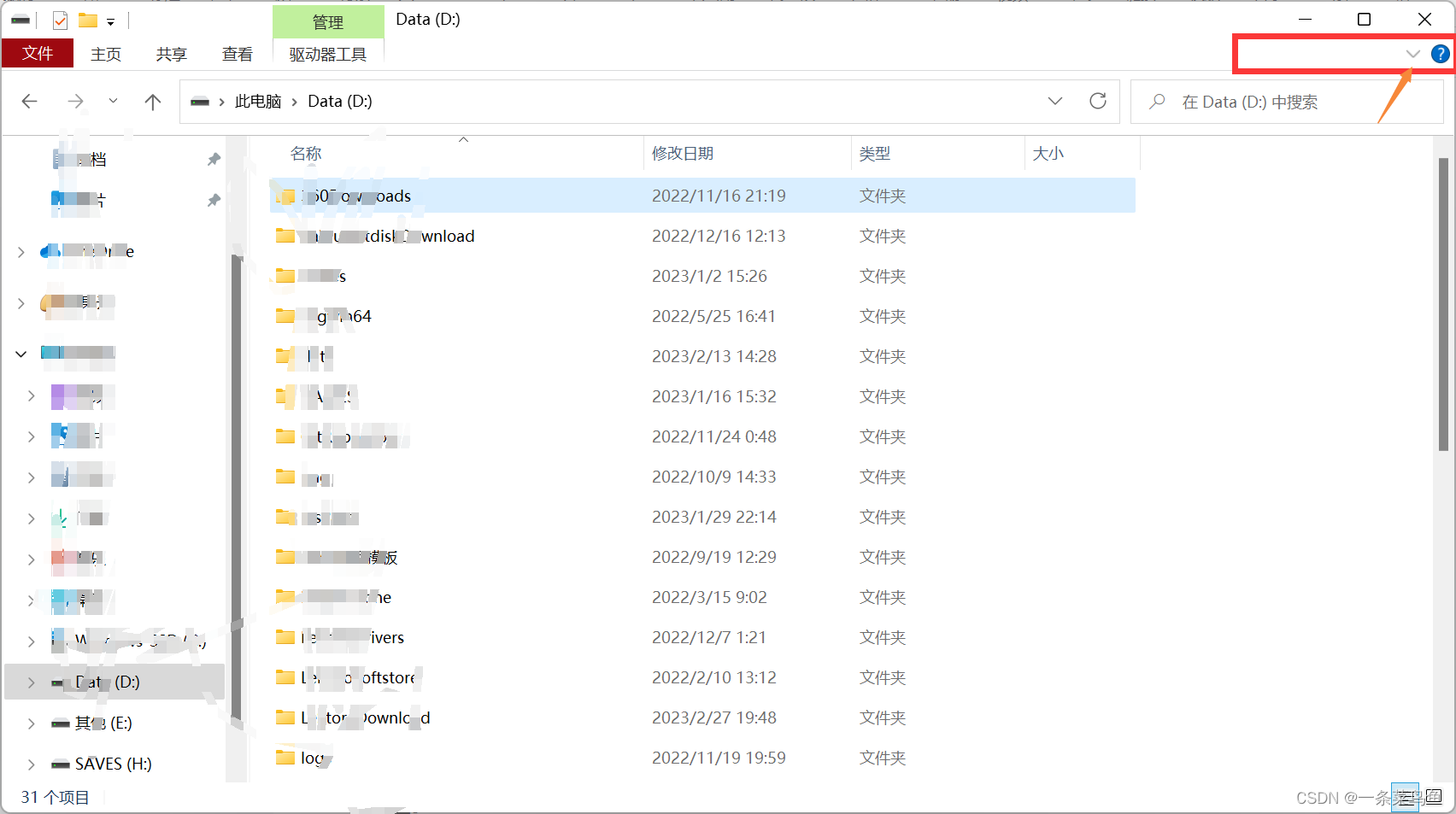
Win11 文件夹打开慢或卡顿解决方案
问题 目前是 2023/2/27, 我的 Win11 系统点开一个文件夹要等待 2-3 秒才能加载出来, 使用体验极差。网上查阅大量资料, 有些人在系统更新后这个情况就消失了, 但是我这一直存在, 系统也是当前的最新版, 没有修复。 目前得出的结论是, 因为 Win11 的工具栏占用了过多的资源, 需…...
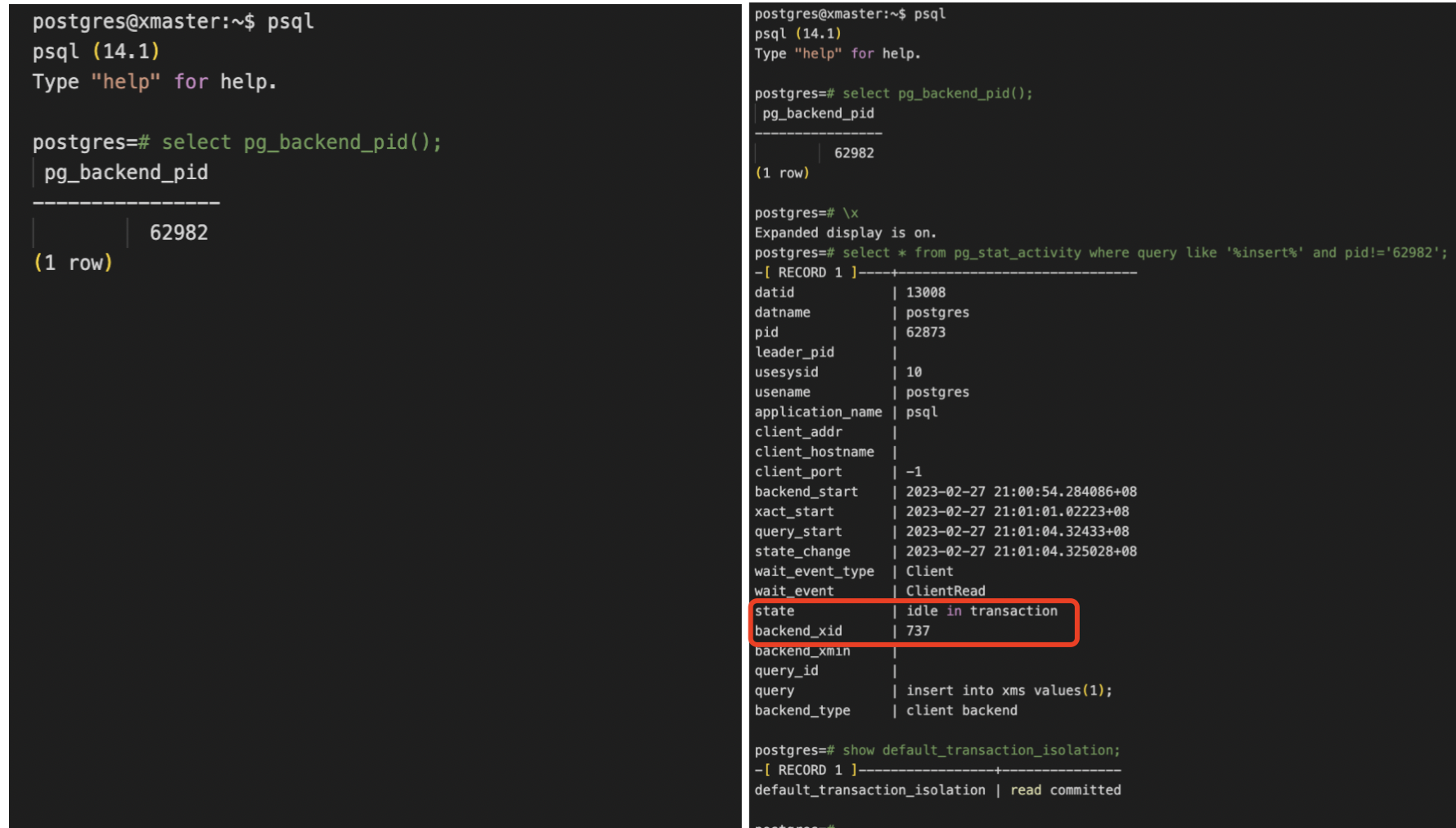
【PostgreSQL的idle in transaction连接状态】
在平时查询pg_stat_activity这个视图的时候,每一行包含了一个进程的相关信息,包含当前正在执行的SQL,或者会话的状态等等,state字段表示当前进程的状态。在PostgreSQL数据库里,其实代码里总共定义了7种BackendState&am…...
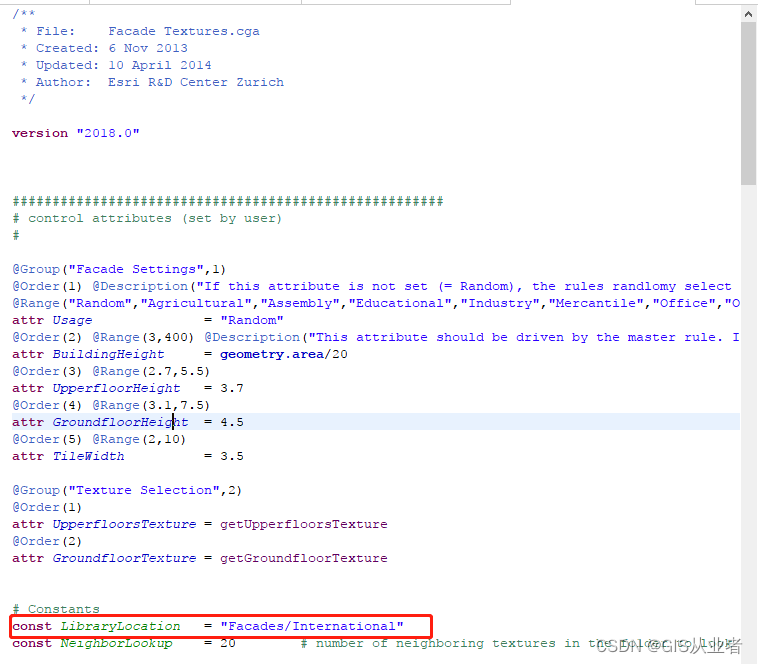
cityengine自定义纹理库资源
背景 cityengine虽然可以将shp生成带纹理的三维模型,但是纹理不一定满足我们的要求,这时候我们就想用我们自己制作的纹理 粗略了解规则文件 了解Building_From_Footprint.cga这个规则文件,具体文件位置默认在 “C:\Users[电脑用户名:如Administrator]\Documents\CityEng…...
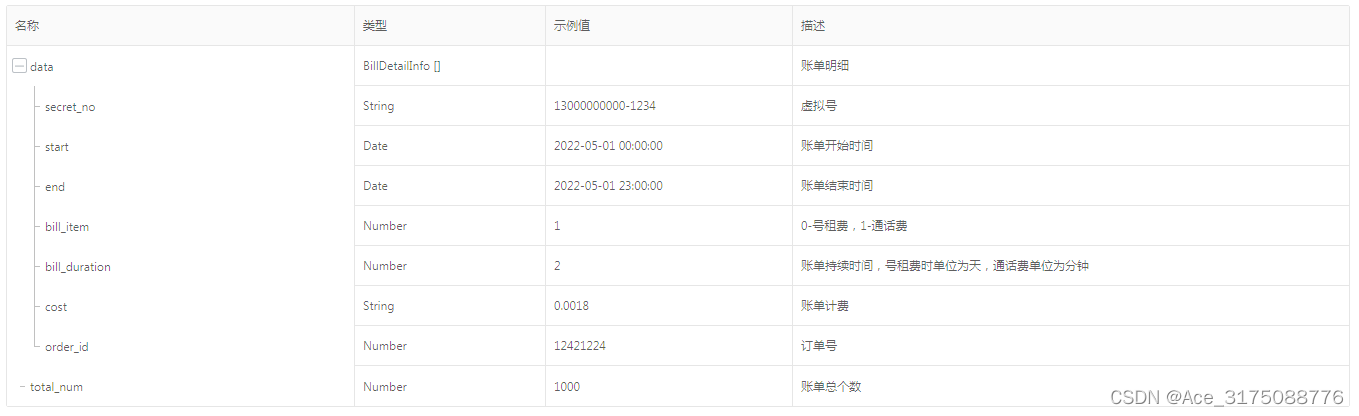
taobao.top.secret.bill.detail( 服务商的商家解密账单详情查询 )
¥免费必须用户授权 服务商的商家解密账单详情查询,仅对90天内的账单提供SLA保障。 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 公共响应参数: 请求参数 响应参数 点击获取key和secret 请求示例 TaobaoClient…...

2023软件测试金三银四常见的软件测试面试题-【抓包和网络协议篇】
八、抓包与网络协议 8.1 抓包工具怎么用 我原来的公司对于抓包这块,在App的测试用得比较多。我们会使用fiddler抓取数据检查结果,定位问题,测试安全,制造弱网环境; 如:抓取数据通过查看请求数据,请求行&…...

vue脚手架多页自动化生成实践
前言 在前端开发过程中,常常面对多种业务场景。到目前为止,前端对于不同场景的处理通常会采用不同的渲染方案来组合处理,常见的渲染方案包括:CSR(Client Side Rendering)、SSR(Server Side Rendering)、SSG(Static Site Generati…...

【SQL语句优化】
SQL语句优化是提高数据库查询性能的重要手段之一,下面是几种常见的SQL语句优化方法和案例: 减少查询的数据量 减少查询的数据量:使用 WHERE 子句和索引来限制检索行数,只检索需要的行,避免检索全部行数据。 例子&am…...

阿里P8:做测试10年我的一些经验分享,希望你们少走弯路
我是在2015年毕业的,当时是读的普通本科,不上不下的专业水平,毕业的时候,恰好遇到了金融危机。校园招聘里阴差阳错的巧合,让我走上了软件测试工程师的道路。 入职第一天,来了个高大上的讲师,记…...
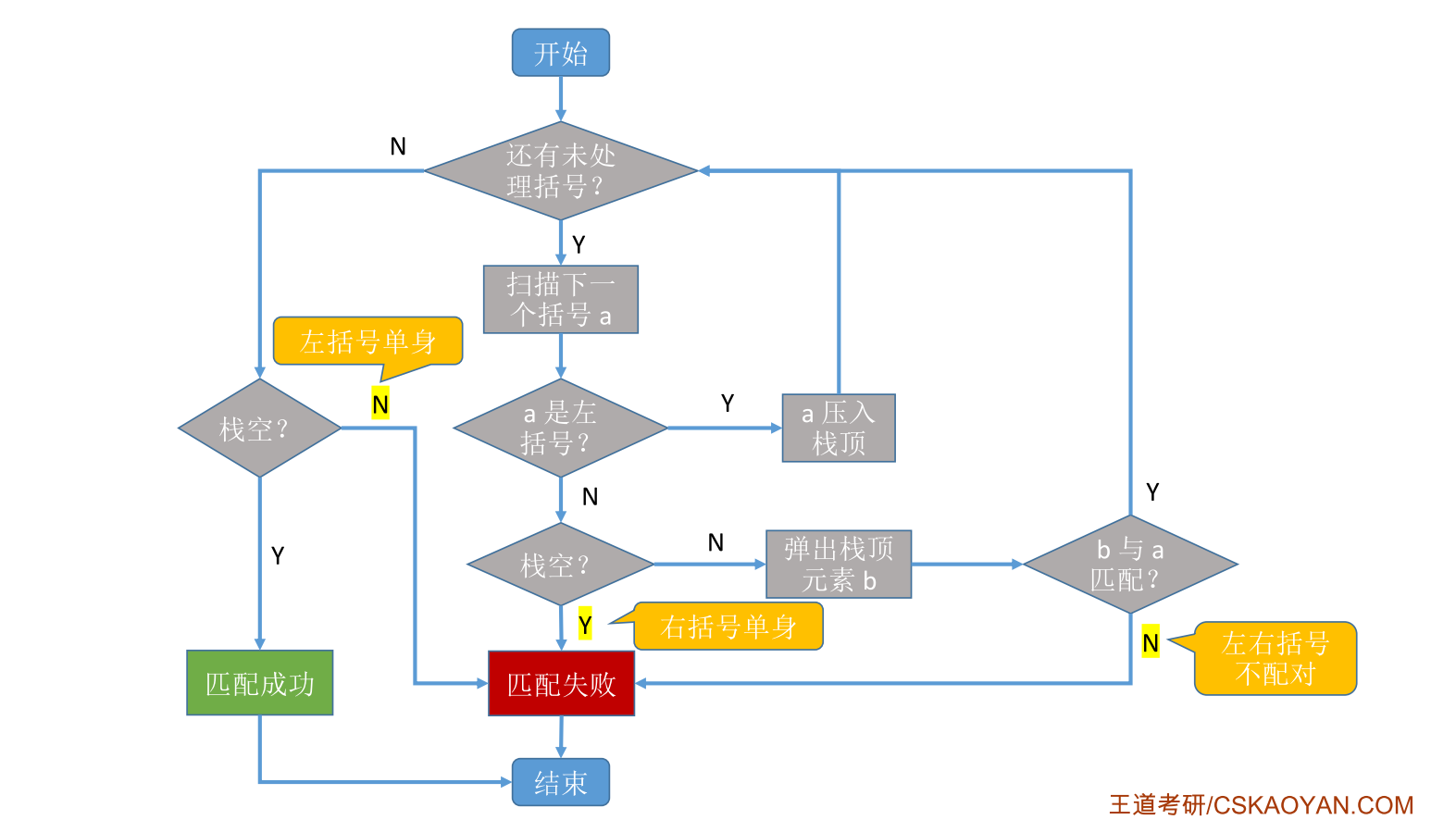
栈在括号匹配中的应用(栈/链栈 纯C实现)
目录 1 问题背景 2 具体思路 3 代码实现 3.1 顺序栈实现 3.2 链栈实现 1 问题背景 栈的括号匹配问题是指在给定一个字符串(包含多种括号),判断其中的括号是否能够正确匹配,即每个左括号是否有一个对应的右括号与之匹配&#x…...
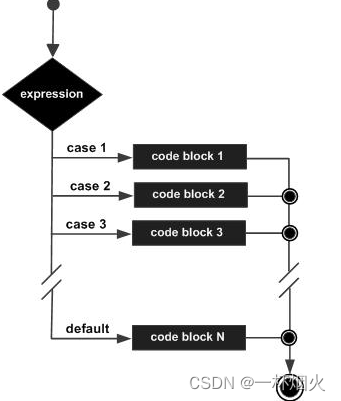
C语言Switch语句用法
C switch 语句 一个 switch 语句允许测试一个变量等于多个值时的情况。每个值称为一个 case,且被测试的变量会对每个 switch case 进行检查。 语法 C 语言中 switch 语句的语法: switch(expression){case constant-expression :statement(s);break;…...

Curl编码请求参数,API接口请求示例参数
请求参数请求参数:num_iid610947572360 参数说明:num_iid:1688商品ID sales_data:&sales_data1 获取近30天成交数据 agent:&agent1 获取1688分销代发价格数据请求示例 测试入口 Curl PHP PHPsdk JAVA C# Python-- 请求示例 url 默认请求参数已经…...

【C/C++】类型限定符extern、const、Volatile、register
1、extern: 声明一个变量,extern声明的变量没有建立存储空间。 extern int a ; //变量在定义的时候创建存储空间。 ①当我们在编译器中试图运行以下代码,系统会报错。 错误原因是“无法解析外部符号_a”.系统认为变量a是没有开辟内存空间的…...
day54【代码随想录】二刷数组
文章目录前言一、二分查找(力扣724)二、移除元素(力扣27)【双指针】三、有序数组的平方(力扣977)【双指针】四、合并两个有序数组(力扣88)五、长度最小的子数组(力扣209&…...
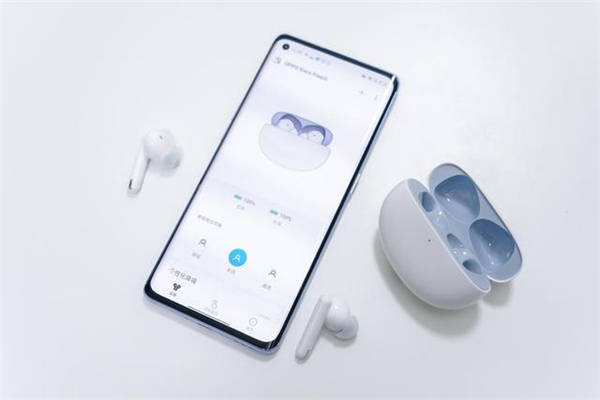
哪个品牌蓝牙耳机性价比高?性价比高的平价蓝牙耳机推荐
现如今,随着蓝牙技术的进步,蓝牙耳机在人们日常生活中的便捷性更胜从前。越来越多的蓝牙耳机品牌被大众看见、认可。那么,哪个品牌的蓝牙耳机性价比高?接下来,我给大家推荐几款性价比高的平价蓝牙耳机,一起…...

揭秘关于TFRcord的五脏六腑
揭秘关于TFRcord的五脏六腑 前言:本篇文章将演示如何创建、解析和使用tf.Example消息,以及如何在.tfrecord文件之间对tf.Example消息进行序列化、写入和读取。 教程讲解使用的都是结构化数据,文章最后还会演示如果将图片写成.tfrecord文件&am…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
