解读CRC校验计算
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu)
参考:http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html
参考:https://en.wikipedia.org/wiki/Cyclic_redundancy_check
参考:https://www.cnblogs.com/yikoulinux/p/14952297.html
参考:https://crccalc.com/
CRC校验定义:
循环冗余校验码(CRC – Cyclic Redundancy Checksum),简称循环码,是一种常用的、具有检错、纠错能力的校验码,在早期的通信中运用广泛。
循环冗余校验码常用于外存储器和计算机同步通信的数据校验。
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data.
最简单的错误检验方法,奇偶检验,实际上是一个1bit的CRC,它使用生成多项式x+1(0b11),被成为CRC-1。
The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms),[3] and has the name CRC-1.
关于CRC校验的理解:
CRC校验的思路是,把一个串作为一个长的数值,附加某段校验码后,形成一个更长的数值串,对该数值串求余运算时能够整除;从而来校验内容未被篡改;
求余运算和每一位的数值都相关,所以校验码会受其每一位修改的影响;
另外,能被整除的概率,和补取的校验码段长度相关,且通常只有一个取值是能整除的,对于1字节校验码来说,概率是1/256,对于4字节校验码来说,概率是1/2^32,校验正确率还是比较高的;
被附加的某段校验码就称之为CRC校验码。
按照这个校验思路,举个10进制的例子:
例如1位校验码,对9求余,1000这个数值校验时,先补全一位0,10000%9,得到值1111,余数1;
如果要整除,就要9-1,补一个8在后面;10008 % 9 可以整除。所以1000后面的CRC校验码就为8。
实际求余的计算,为了提升校验效率,采用的模二除法:
对于模二除法,与算术除法不同的是每一位除的结果不影响其他位,即不向上借位,所以实际上相当于二进制中的逻辑异或运算。
0 mod 1 = 1 --> 0 ^ 1 = 1
1 mod 0 = 1 --> 1 ^ 0 = 1
0 mod 0 = 0 --> 0 ^ 0 = 0
1 mod 1 = 0 --> 1 ^ 1 = 0
另外,模二加法,模二减法与这个规律也一致,也与异或效果一致
0 + 1 = 0 - 1 = 1
1 + 0 = 1 - 0 =1
0 + 0 = 0 - 0 = 0
1 + 1 = 1 - 1 = 0
模二乘法不同,和 按位与& 结果一致 1 * 1 = 1 --> 1 & 1 = 1
对于异或算法来说:满足交换律,三者还能互为求值,非常适合互为计算(ps. 简单加密解密值非常适合)
a ^ b = b ^ a = c
a ^ c = c ^ a = b
b ^ c = c ^ b = a
这样来说,一个串str如果要获得它的CRC校验串,流程就是:
a. 对该串str补二进制0,补0的长度为crc校验码的二进制长度
b. 对补0后的串进行模二除法,获取到余数,余数就是补值 ( 0 ^ a = b --> b ^ a = 0)
c. 把补值放到该串str的后面,作为CRC校验码
对于所使用的除数,多项式规律为:
crc8 常用 x^8 + x^2 + x + 1,首位是比较对齐用,剩余值为 0x07,二进制逆序为 0xE0
crc16 常用 x^16 + x^15 + x^2 + 1,首位是比较对齐用,剩余值为 0x8005,二进制逆序为0xA001
crc32 常用 x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1,首位用于比较对齐,剩余值为 0x04C11DB7,二进制逆序为0xEDB88320
对于CRC的计算简化:
CRC计算时,一般都是使用查表法计算的;
假设一个字符串长度是一个字节,当明确多项式除数之后,那么它的CRC校验值,只可能有256中相对应,也即可以查表得到。
那么对于一个实际字符串来说,可以看作由一个1字节串,1字节串连接组成的长串;
计算时:
a. 把第一个字节的crc值获取到之后,带入到下一个字节的计算中;
b. 把crc首个字节与当前字节合并,合成值查表,获取到一个新的crc值,再把上一个crc的剩余字节移位后合并到crc新值上,得到合并后的值;
c. 依次类推,等到字符串末尾时,就获取到了最终的crc值;
CRC参数:
CRC的关键必选的参数是width和polynomial;CRC校验宽度width,例如8字节,16字节,32字节,标识了产生CRC校验值的位宽;CRC多项式polynomial,例如crc8常用的 x8+x2+x+1,是crc校验所使用的除数。
除了关键必选参数外,crc扩展出了initVal初始值,xorValue结果xor值,refect-in输入值位镜像, refect-out输出值位镜像参数,增加了crc校验计算的复杂度;
综上这些参数的设定,也被分别应用到不同的领域,不同的场景。
8字节的一个例子:
对于8字节的计算,参考如下
unsigned char charcrc8(const unsigned char ch, bool reflect=false){unsigned char crc = ch;if (!reflect){const unsigned char polynomial = 0x07;for (int i=0; i<8; i++){if ((crc & 0x80) != 0)crc = (crc << 1) ^ polynomial;elsecrc <<= 1;}}else{const unsigned char polynomial = 0xE0;for (int i=0; i<8; i++){if ((crc & 0x1) != 0)crc = (crc >> 1) ^ polynomial;elsecrc >>= 1;}}return crc;
}
unsigned char calccrc8(const char* str, int count, unsigned char init = 0, bool reflect=false, unsigned char xorcrc = 0){unsigned char crc = init;for (int i=0; i<count; i++){crc = charcrc8(str[i] ^ crc, reflect); }return crc ^ xorcrc;
}
简单的调用例子:
int main(int argc, char** argv)
{const char* str="123";if (argc >= 2) str = argv[1];for (int i=0; i<256; i++){printf("(%d->0x%02x-0x%02x) ", i, charcrc8(i), charcrc8(i, true));}printf("\n\n");printf("<%s> crc8 is 0x%02x, with reflect 0x%02x\n", str, calccrc8(str, strlen(str)), calccrc8(str, strlen(str), 0, true));return 0;
}
再附一些参考地址:
crc在线计算:https://crccalc.com/
crc计算方法:http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html
reflect-table如何构建出来:https://stackoverflow.com/questions/28656471/how-to-configure-calculation-of-crc-table
crc在线计算:http://www.sunshine2k.de/coding/javascript/crc/crc_js.html
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu)
相关文章:

解读CRC校验计算
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 参考:http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html 参考:https://en.wikipedia.org/wiki/Cyclic_redundancy_check 参考:https://www.cnblogs.com/…...
深入理解Spring MVC下
上一篇博客从理论概念上来梳理Spring MVC相关知识,此篇博客将通过spring官网提供showcase代码为例子,详细介绍showcase代码中包含的各个例子是如何实现的。官网的showcase代码包含的主要例子包括,Demo地址:Mapping Requests&#…...

【Linux】ssh-keygen不需要回车,自动生成密钥,批量免密操作!
使用命令ssh-keygen 需要手动敲击回车,才会生成密钥,如下代码所示 [rootlocalhost ~]# ssh-keygen Generating public/private rsa key pair. Enter file in which to save the key (/root/.ssh/id_rsa): Enter passphrase (empty for no passphrase):…...

C/C++开发,无可避免的内存管理(篇四)-智能指针备选
一、智能指针 采用C/C开发堆内存管理无论是底层开发还是上层应用,无论是开发新手,还是多年的老手,都会不自觉中招,尤其是那些不是自己一手经历的代码,要追溯问题出在哪里更是个麻烦事。C/C程序常常会遇到程序突然退出&…...
VMware ESXi给虚拟机扩容
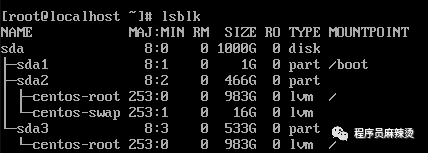
用ESXi管理的虚拟机硬盘空间不够了,讲一下如何进行扩容。 一、查看现状 通过如下三个命令,可以查看硬盘情况,可以看到只有500G,已经用了45%。这次我们再扩容500G。 df -Th lsblk fdisk -lIDE磁盘的文件名为 /de…...
认识STM32和如何构建STM32工程
STM32介绍什么是单片机单片机(Single-Chip Microcomputer)是一种集成电路芯片,把具有数据处理能力的中央处理器CPU、随机存储器RAM、只读存储器ROM、多种/0口和中断系统、定时器/计数器等功能(可能还包括显示驱动电路、脉宽调制电路、模拟多路转换器、A/D转换器等电…...

RabbitMQ延迟队列
目录 一、概念 二、使用场景 三、RabbitMQ 中的 TTL (一)队列设置 TTL (二)消息设置 TTL (三)两者的区别 四、整合SpringBoot实现延迟队列 (一)创建项目 (二&am…...
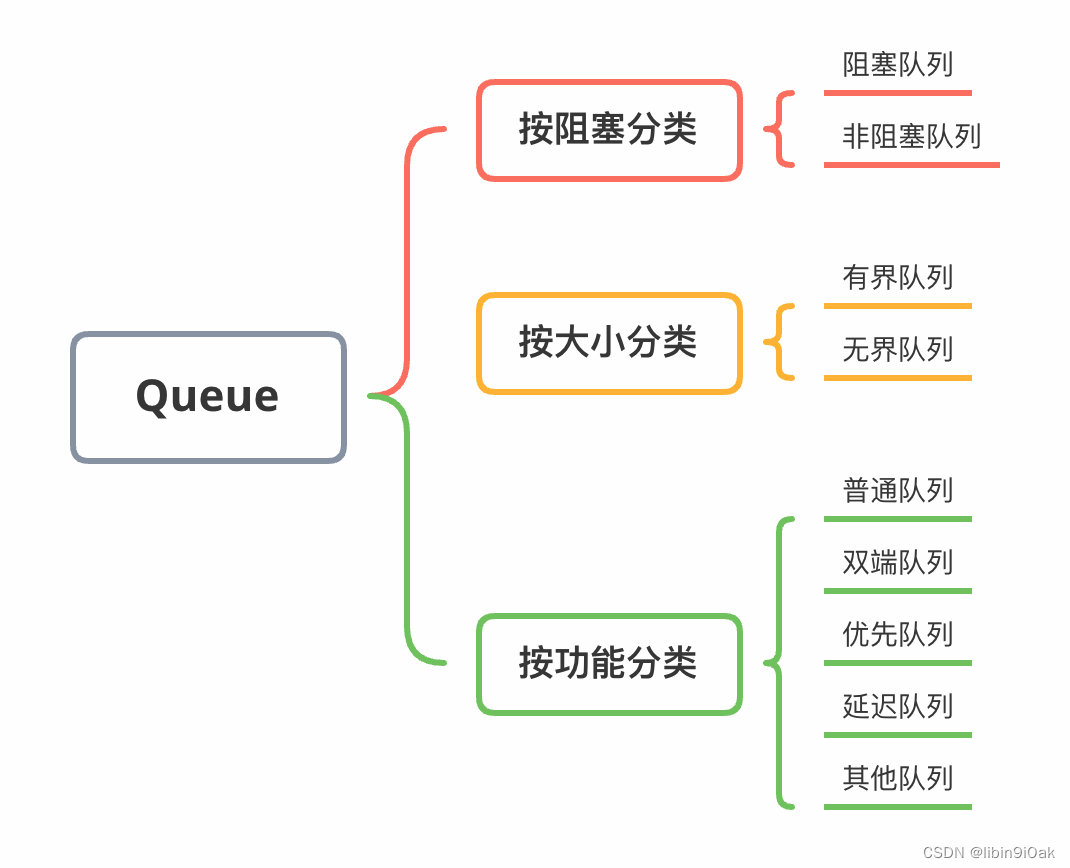
Java中常用的七种队列你了解多少?
文章目录Java中常用的七种队列你了解多少?ArrayBlockingQueue队列如何使用?添加元素到队列获取队列中的元素遍历队列LinkedBlockingQueue队列如何使用?1. 创建SynchronousQueue对象2. 添加元素到队列3. 获取队列中的元素4. 遍历队列SynchronousQueue队列…...
)
<Java获取时间日期工具类>常见八种场景(一)
一:自定义时间日期工具类常用的八种方式(整理): 0,getTimeSecondNum:时间日期转成秒数,常用于大小比较 1,getLastYearMonthLastDay:获取去年当月最后一天的时间日期 2,getLastYearM…...

接上一篇 对多个模型环形旋转进行优化 指定旋转位置
using System.Collections; using System.Collections.Generic; using UnityEngine; using DG.Tweening; public class ModelAnimal : MonoBehaviour { //记录鼠标滑动 public Vector2 lastPos;//鼠标上次位置 Vector2 currPos;//鼠标当前位置 Vector2 offset;//两次位置的偏移…...
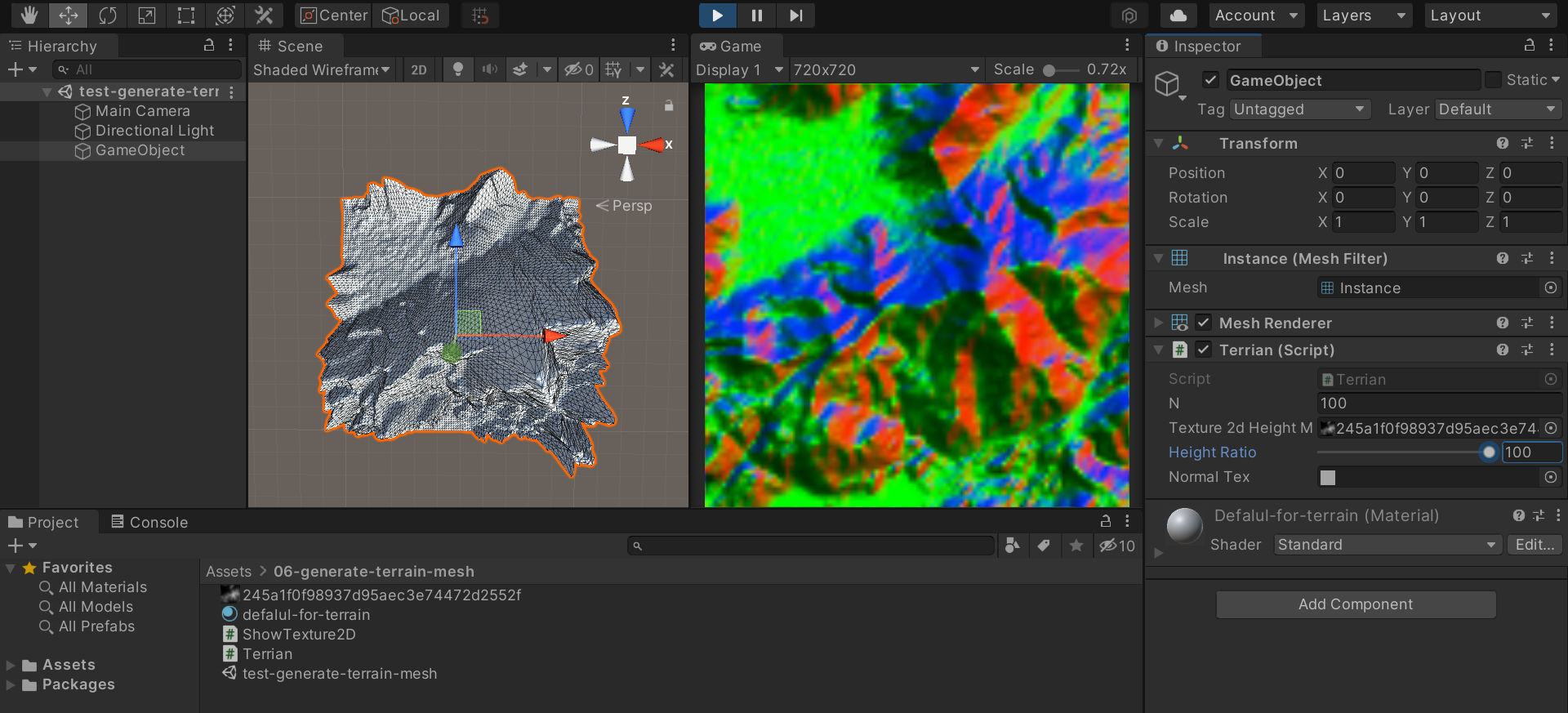
Unity中获取地形的法线
序之前,生成了地形图:(42条消息) 从灰度图到地形图_averagePerson的博客-CSDN博客那末,地形的法线贴图怎么获取?大概分为两个部分吧,先拿到法线数据,再画到纹理中去。关于法线计算Unity - Scripting API: M…...
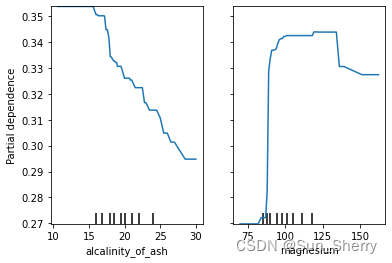
模型解释性:PFI、PDP、ICE等包的用法
本篇主要介绍几种其他较常用的模型解释性方法。 1. Permutation Feature Importance(PFI) 1.1 算法原理 置换特征重要性(Permutation Feature Importance)的概念很简单,其衡量特征重要性的方法如下:计算特征改变后模型预测误差的增加。如果打乱该特征的…...
)
spring常见面试题(2023最新)
目录前言1.spring是什么2.spring的设计核心是什么3.IOC和AOP面试题4.spring的优点和缺点5.spring中bean的作用域6.spring中bean的注入方式7.BeanFactory 和 ApplicationContext有什么区别?8.循环依赖的情况,怎么解决?9.spring中单例Bean是线程…...

华为OD机试题,用 Java 解【压缩报文还原】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
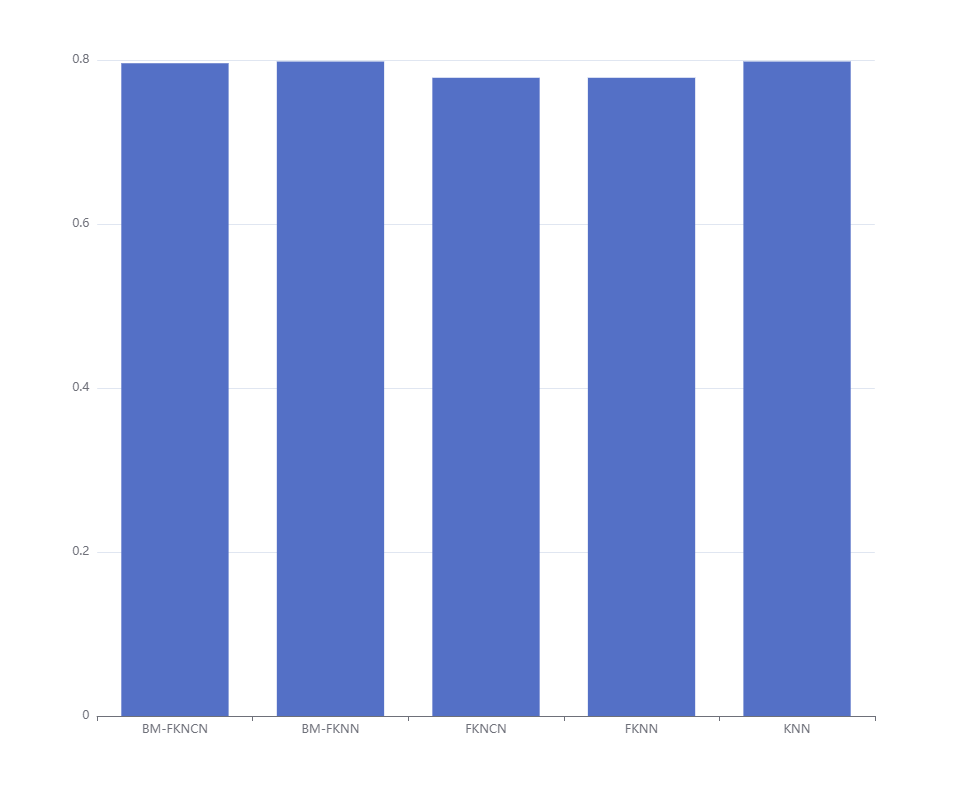
机器学习-BM-FKNCN、BM-FKNN等分类器对比实验
目录 一、简介和环境准备 二、算法简介 2.1四种方法类: 2.1.1FKNN 2.1.2FKNCN 2.1.3BM-FKNN 2.1.3BM-FKNCN 2.2数据预处理 2.3输出视图 2.4调用各种方法看准确率 2.4.1BM-FKNCN 2.4.2BM-FKNN 2.4.3FKNCN 2.4.4FKNN 2.4.5KNN 一、简介和环境准备 k…...

ChatGPT火了,对话式人工智能还能干嘛?
身兼数职的ChatGPT 从2022火到了2023 连日来一直是各大平台的热议对象 其实除了写诗、敲代码、处理文档 以ChatGPT为代表的 对话式人工智能 还有更重要的工作要做 对话式AI与聊天机器人 相信大多数人…...
)
十一、操作数栈的特点(Operand Sstack)
1.每一个独立的栈帧中除了包含局部变量表以外,还包含一个后进先出的操作数栈,也可以称之为表达式栈。 2.操作数栈,在方法执行过程中,根据字节码指令,往栈中写入数据,或提取数据,即入栈ÿ…...

拆解瑞幸新用户激活流程,如何让用户“动”起来?
Aha时刻 一个产品的拉新环节,是多种方式并存的;新用户可能来自于商务搭建了新的渠道,运营策划了新的活动,企划发布了新的广告,销售谈下了新的客户,市场推广了新的群体,以及产品本身的口碑传播,功能更新带来的自然流量。 这是一个群策群力的环节,不同的团队背负不同的K…...
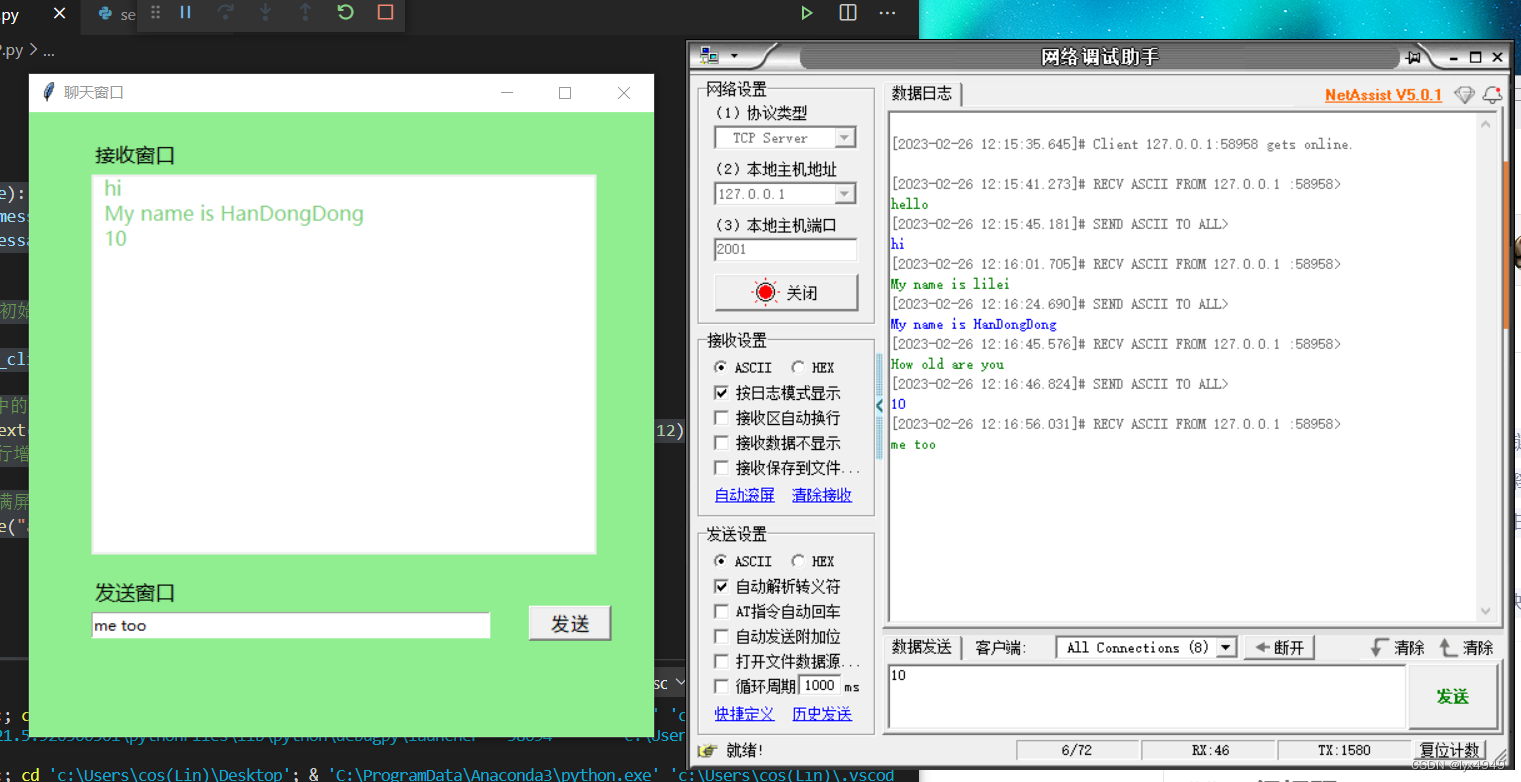
tkinter界面的TCP通信/开启线程等待接收数据
前言 用简洁的语言写一个可以与TCP客户端实时通信的界面。之前做了一个项目是要与PLC进行信息交互的界面,在测试的时候就利用TCP客户端来实验,文末会附上TCP客户端。本文分为三部分,第一部分是在界面向TCP发送数据,第二部分是接收…...

华为OD机试题,用 Java 解【任务混部】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
