C/C++排序算法(二) —— 选择排序和堆排序
文章目录
- 前言
- 1. 直接选择排序
- 🍑 基本思想
- 🍑 具体步骤
- 🍑 具体步骤
- 🍑 动图演示
- 🍑 代码实现
- 🍑 代码升级
- 🍑 特性总结
- 2. 堆排序
- 🍑 向下调整算法
- 🍑 任意树调整为堆的思想
- 🍑 堆排序
- 🍑 动图演示
- 🍑 完整代码
- 🍑 特性总结
- 3. 总结
前言
今天我们将学习排序算法中的 直接选择排序 和 堆排序,它们的本质就是在选择,所以这两个可以统称为 选择排序。
1. 直接选择排序
🍑 基本思想
选择排序(Selection-sort)是一种简单直观的排序算法。
它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
🍑 具体步骤
相信大家都上过体育课吧,一般第一节体育课的时候,老师都会让大家排好队然后按照个头从矮到高进行排序,假设有 5 名同学。
首先老师找到了个子最矮的 5 号同学,然后老师说:5 号同学,你是最矮的,跟 1 号交换一下位置!
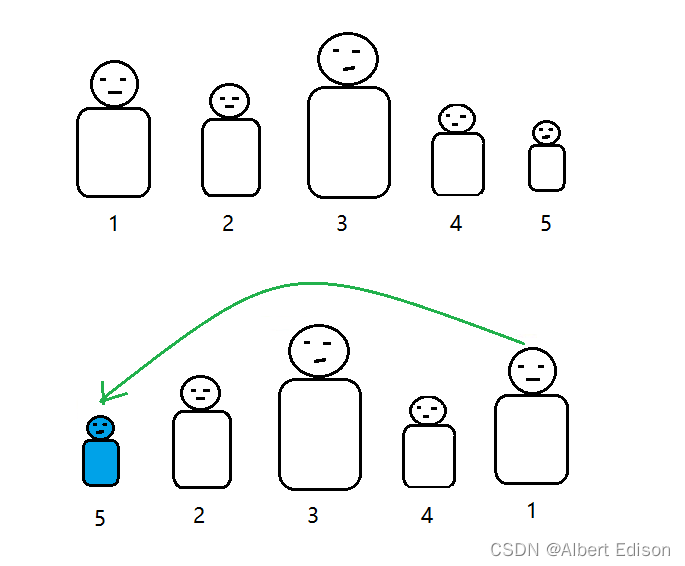
这时候,老师又说:4 号同学,你是第二矮的,跟 2 号交换一下位置!
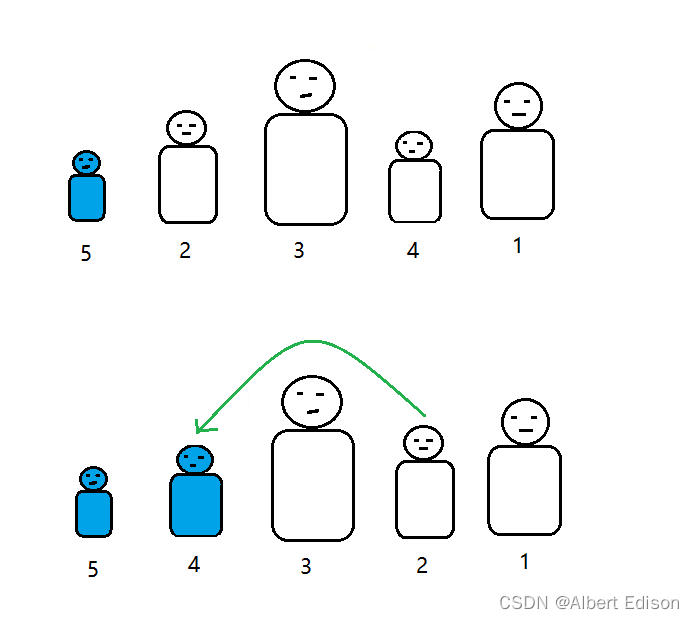
老师又说:2 号同学,你是第三矮的,你和 3 号交换一下位置!
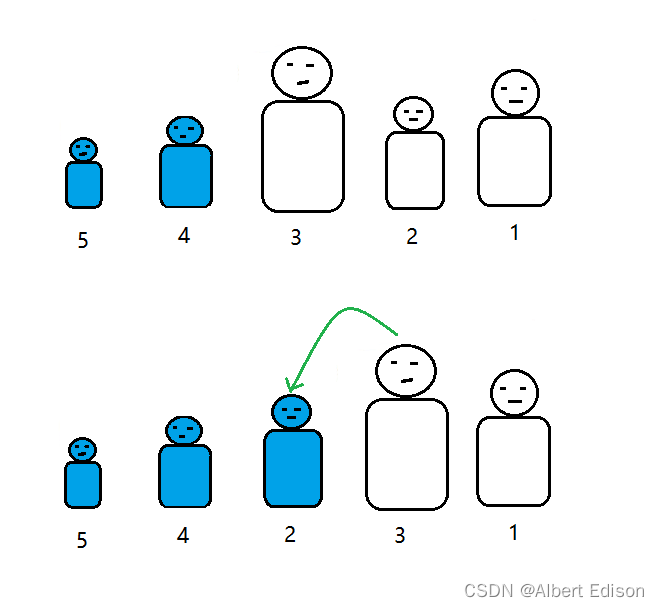
最后,老师说:1 号同学,你是第四矮的,你和 3 号交换一下位置吧!
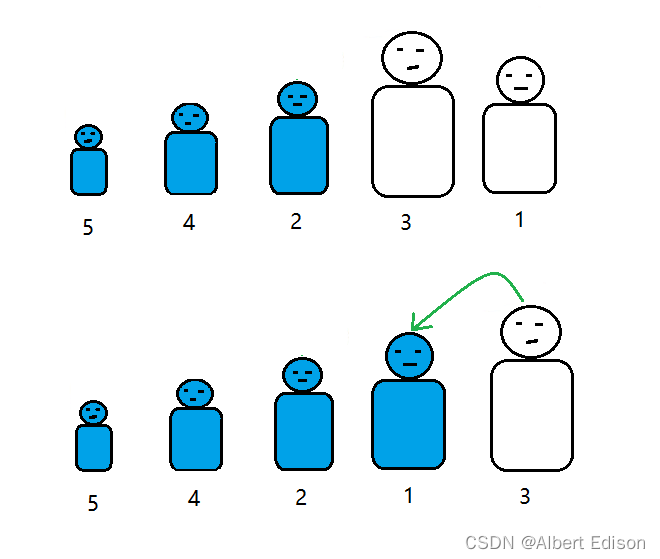
如此一来,每一轮选出最小者直接交换到左侧的思路,就是选择排序的思路。这种排序的最大优势就是省去了多余的元素交换。

🍑 具体步骤
算法实现:
(1)在元素集合 array[i] 到 array[n-1] 中选择关键码最大(小)的数据元素。
(2)若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。
(3)在剩余的 array[i] 到 array[n-2](array[i+1] 到 array[n-1])集合中,重复上述步骤,直到集合剩余 1 个元素。
🍑 动图演示
我们来看看选择排序的动图演示吧

🍑 代码实现
代码示例
//交换函数
void Swap(int* pa, int* pb) {int tmp = *pa;*pa = *pb;*pb = tmp;
}//选择排序(一次选一个数)
void SelectSort(int* a, int n)
{int i = 0;for (i = 0; i < n; i++)//i代表参与该趟选择排序的第一个元素的下标{int start = i;int min = start;//记录最小元素的下标while (start < n){if (a[start] < a[min])min = start;//最小值的下标更新start++;}Swap(&a[i], &a[min]);//最小值与参与该趟选择排序的第一个元素交换位置}
}
🍑 代码升级
实际上,我们可以一趟选出两个值,一个最大值和一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
代码示例
//交换函数
void Swap(int* pa, int* pb) {int tmp = *pa;*pa = *pb;*pb = tmp;
}//直接选择排序(优化版本)
void SelectSort(int* a, int n) {int left = 0;int right = n - 1;while (left < right) {int mini = left;int maxi = left;//遍历区间:[left+1, right]//选出最小的和最大的,然后交换for (int i = left + 1; i <= right; ++i) {//选出最小的数if (a[i] < a[mini]) {mini = i;}//选出最大的数if (a[i] > a[maxi]) {maxi = i;}}Swap(&a[left], &a[mini]); //把最小的数放在最左边//如果left和maxi重叠,修正一下maxi即可if (left == maxi) {maxi = mini;}Swap(&a[right], &a[maxi]); //把最大的数放在最右边left++;right--;}
}
🍑 特性总结
-
直接选择排序思考非常好理解,但是效率不是很好,实际中很少使用。
-
时间复杂度:O(N2)O(N^2)O(N2)
-
空间复杂度:O(1)O(1)O(1)
-
稳定性:不稳定
2. 堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序。
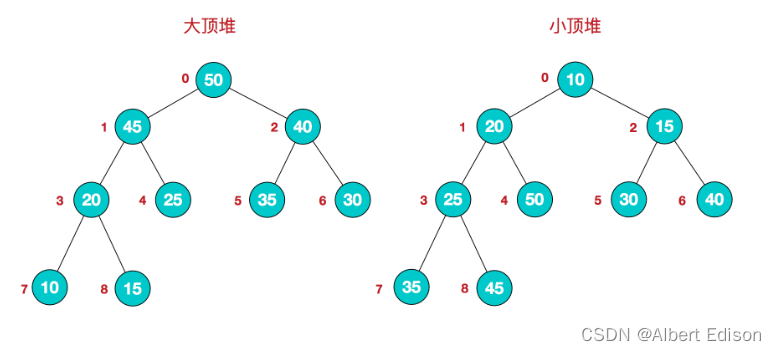
堆是具有以下性质的完全二叉树:
(1)每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
(2)或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
如下图所示,就是两种堆的类型:
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子:
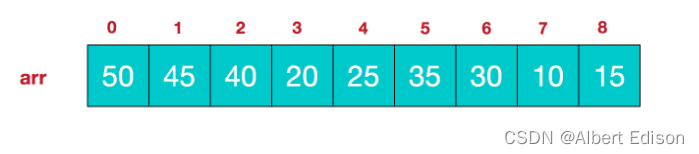
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
-
大顶堆:
arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] -
小顶堆:
arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
🍑 向下调整算法
既然要进行堆排序,那么就要建堆,而建堆的方式有两种:
-
使用向上调整,插入数据的思想建堆,但是时间复杂度为:O(N∗logN)O(N*logN)O(N∗logN)
-
使用向下调整,插入数据的思想建堆,时间复杂度为:O(N)O(N)O(N)
所以我们这里推荐使用 堆的向下调整算法,那么建堆也是有 2 个前提的:
(1)如果需要从⼤到⼩排序,就要将其调整为小堆,那么根结点的左右子树必须都为小堆。
(2)如果需要从⼩到⼤排序,就要将其调整为大堆,那么根结点的左右子树必须都为大堆。
但是我们先了解一下什么叫做大堆,如下图:

注意:有一个概念别搞错了,调整大堆并不是把元素从大到小排列,而是每个根节点都比它的叶子节点大
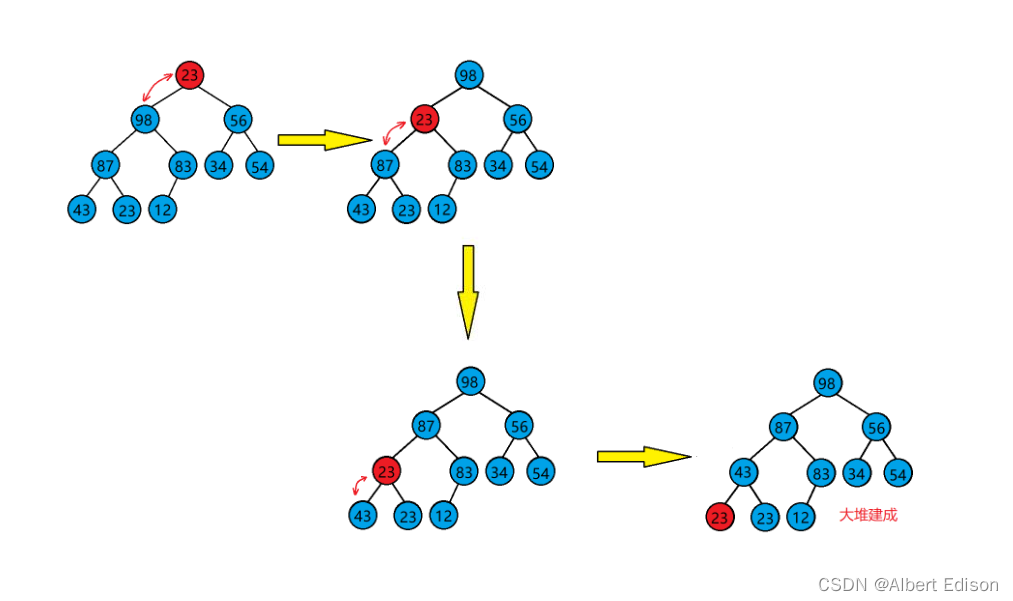
向下调整建大堆算法的基本思想:
(1)从根结点处开始,选出左右孩子中值较大的孩子,让大的孩子与其父亲进行比较
(2)若大的孩子比父亲还大,则该孩子与其父亲的位置进行交换。并将原来大的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。
(3)若大的孩子比父亲小,则不需处理了,调整完成,整个树已经是大堆了。
如下图所示:
堆的向下调整算法代码
//向下调整大堆
void AdjustDownBig(HPDataType* a, size_t size, size_t root) {size_t parent = root;size_t child = 2 * parent + 1; //默认左孩子最大while (child < size){//1.找出左右孩子中小的那个//如果右孩子存在,且右孩子小于size(元素个数),那么就把默认小的左孩子修改为右孩子if (child + 1 < size && a[child + 1] > a[child]) {++child;}//2.把小的孩子去和父亲比较,如果比父亲小,就交换if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else {break; //如果孩子大于等于父亲,那么直接跳出循环}}
}
使用堆的向下调整算法,最坏的情况下(即一直需要交换结点),需要循环的次数为:h−1h - 1h−1 次( h 为树的高度)。
而 h=log2(N+1)h = log2(N+1)h=log2(N+1)( N 为树的总结点数)。
所以堆的向下调整算法的时间复杂度为:O(logN)O(logN)O(logN) 。
🍑 任意树调整为堆的思想
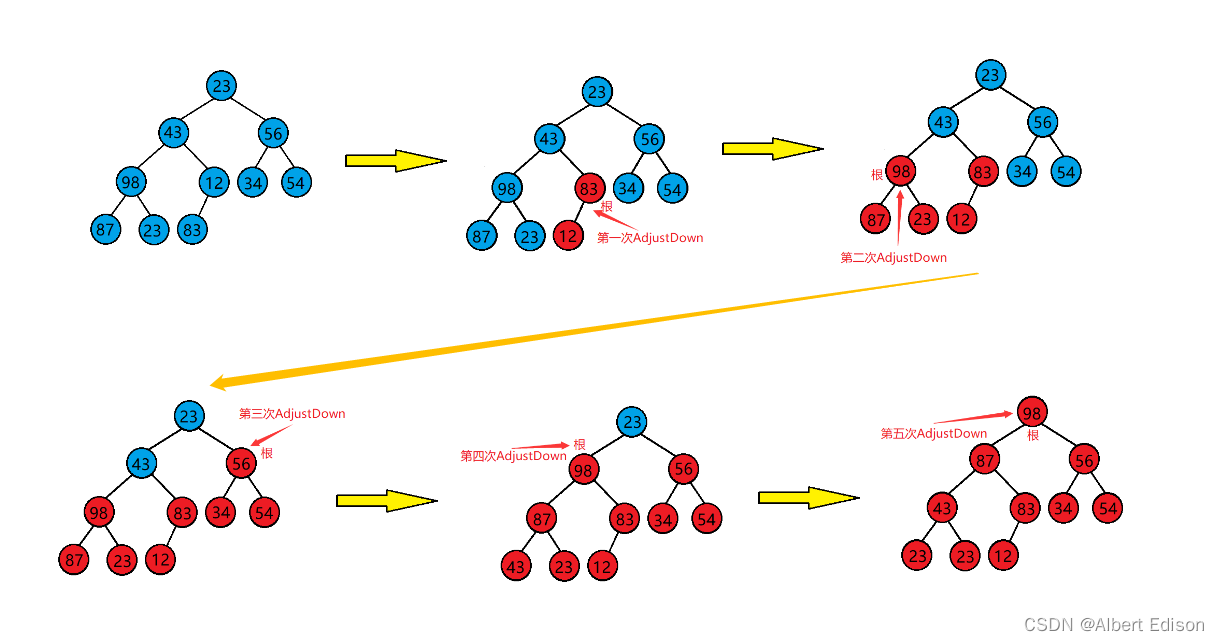
上面说到,使用堆的向下调整算法需要满足其根结点的左右子树均为大堆或是小堆才行,那么如何才能将一个任意树调整为堆呢?
答案很简单,我们只需要从 倒数第一个非叶子结点 开始,从后往前,按下标,依次作为根去向下调整即可。
注意:倒数第一个非叶子结点,即为最后一个节点的父亲,也被叫做根。
如图所示:
建堆代码
//从倒数第一个非叶子节点开始(最后一个节点的父亲)
//n-1是最后一个节点的下标,(n-1-1)/2最后一个节点的父亲的下标
for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDownBig(a, n, i);
}
那么建堆的时间复杂度又是多少呢?
当结点数无穷大时,完全二叉树与其层数相同的满二叉树相比较来说,它们相差的结点数可以忽略不计,所以计算时间复杂度的时候我们可以将完全二叉树看作与其层数相同的满二叉树来进行计算。
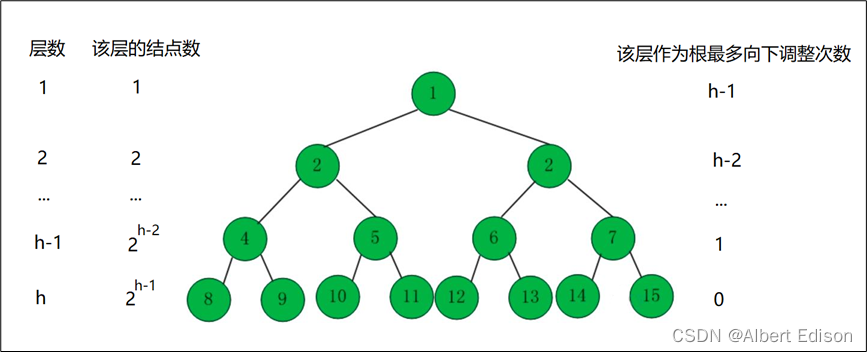
我们计算建堆过程中总共交换的次数:T(n)=1∗(h−1)+2∗(h−2)+...+2h−3∗2+2h−2∗1T(n)=1*(h-1)+2*(h-2)+...+2^{h-3}*2+2^{h-2}*1T(n)=1∗(h−1)+2∗(h−2)+...+2h−3∗2+2h−2∗1
两边同时乘 2 得:2T(n)=2∗(h−1)+22∗(h−2)+...+2h−2∗2+2h−1∗12T(n)=2*(h-1)+2^2*(h-2)+...+2^{h-2}*2+2^{h-1}*12T(n)=2∗(h−1)+22∗(h−2)+...+2h−2∗2+2h−1∗1
两式相减得:T(n)=1−h+21+22+...+2h−2+2h−1T(n)=1-h+2^1+2^2+...+2^{h-2}+2^{h-1}T(n)=1−h+21+22+...+2h−2+2h−1
运用等比数列求和得:T(n)=2h−h−1T(n)=2^h-h-1T(n)=2h−h−1
由二叉树的性质,有 N=2h−1N=2^h-1N=2h−1 和 h=log2(N+1)h=log_2(N+1)h=log2(N+1)
所以:T(n)=N−log2(N+1)T(n)=N-log_2(N+1)T(n)=N−log2(N+1)
那么用大 O 的渐进表示法:T(N)=O(N)T(N)=O(N)T(N)=O(N)
总结一下:
-
堆的向下调整算法的时间复杂度:O(logN)O(logN)O(logN)
-
建堆的时间复杂度:O(N)O(N)O(N)
🍑 堆排序
堆排序的基本思想是:
-
将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
-
将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
-
重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
堆排序代码
void HeapSort(int* a, int n) {//建堆:使用向下调整 --> O(N)//从倒数第一个非叶子节点开始(最后一个节点的父亲)//n-1是最后一个节点的下标,(n-1-1)/2最后一个节点的父亲的下标for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDownBig(a, n, i);}//升序 --> 建大堆size_t end = n - 1; //最后一个元素的下标while (end > 0){Swap(&a[0], &a[end]); //交换第一个元素和最后一个元素AdjustDownBig(a, end, 0);--end;}
}
🍑 动图演示
我们来看一个堆排序的动图过程吧

🍑 完整代码
代码实现
//调整算法里面的交换函数
void Swap(HPDataType* pa, HPDataType* pb) {HPDataType tmp = *pa;*pa = *pb;*pb = tmp;
}//向下调整算法 --> 建大堆
void AdjustDownBig(HPDataType* a, size_t size, size_t root) {size_t parent = root;size_t child = 2 * parent + 1; //默认左孩子最大while (child < size){//1.找出左右孩子中小的那个//如果右孩子存在,且右孩子小于size(元素个数),那么就把默认小的左孩子修改为右孩子if (child + 1 < size && a[child + 1] > a[child]) {++child;}//2.把小的孩子去和父亲比较,如果比父亲小,就交换if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else {break; //如果孩子大于等于父亲,那么直接跳出循环}}
}//堆排序代码
void HeapSort(int* a, int n) {//建堆:使用向下调整 --> O(N)//从倒数第一个非叶子节点开始(最后一个节点的父亲)//n-1是最后一个节点的下标,(n-1-1)/2最后一个节点的父亲的下标for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDownBig(a, n, i);}//升序 --> 建大堆size_t end = n - 1; //最后一个元素的下标while (end > 0){Swap(&a[0], &a[end]); //交换第一个元素和最后一个元素AdjustDownBig(a, end, 0);--end;}
}//主函数
int main()
{int a[] = { 4,2,7,8,5,1,0,6 };HeapSort2(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); ++i) {printf("%d ", a[i]);}return 0;
}
🍑 特性总结
堆排序是一种选择排序,整体主要由 构建初始堆 + 交换堆顶元素和末尾元素并重建堆 两部分组成。
其中构建初始堆经推导复杂度为 O(n)O(n)O(n),在交换并重建堆的过程中,需交换 n−1n-1n−1 次,而重建堆的过程中,根据完全二叉树的性质,[log2(n−1),log2(n−2)...1][log2(n-1),log2(n-2)...1][log2(n−1),log2(n−2)...1] 逐步递减,近似为 nlognnlognnlogn。
所以堆排序时间复杂度一般认为就是O(nlogn)级。
-
堆排序使用堆来选数,效率就高了很多。
-
时间复杂度:O(N∗logN)O(N*logN)O(N∗logN)
-
空间复杂度:O(1)O(1)O(1)
-
稳定性:不稳定
3. 总结

相关文章:

C/C++排序算法(二) —— 选择排序和堆排序
文章目录前言1. 直接选择排序🍑 基本思想🍑 具体步骤🍑 具体步骤🍑 动图演示🍑 代码实现🍑 代码升级🍑 特性总结2. 堆排序🍑 向下调整算法🍑 任意树调整为堆的思想&#…...
爬虫笔记之——selenium安装与使用(1)
爬虫笔记之——selenium安装与使用(1)一、安装环境1、下载Chrome浏览器驱动(1)查看Chrome版本(2)下载相匹配的Chrome驱动程序地址:https://chromedriver.storage.googleapis.com/index.html2、学…...
STC15单片机软串口的使用
STC15软串口的使用📖在没有使用定时器资源的情况下,根据波特率位传输时间,利用STC-ISP工具自动计算出位延时函数。 ✨在官方所提供的库函数中位传输时间函数,仅适用于使用波特率为:9600的串口数据传输: void BitTime(…...
Ansible的脚本------playbook剧本
一、剧本的前置知识点1、主机清单ansible默认的主机清单是/etc/ansible/hosts文件主机清单可以手动设置,也可以通过Dynamic Inventory动态生成一般主机名使用FQDNvi /etc/ansible/hosts [webserver] #使用方括号设置组名 www1.example.org #定…...

实验5-计算中值及分治技术
目录 1.寻找中位数(利用快速排序来寻找中位数) 2.分治方法求数组的和 3.合并排序...

dbeaver从excel导入数据笔记
场景 有excel的数据,需要做到数据库里。 方案一: 开发代码来实现。缺点是需要开发成本。 方案二: 数据库导入工具导入。不用开发,相对快速一些。 这里说下数据库工具导入。 操作过程 1、拿到excel数据文件,根据标题…...

PyTorch学习笔记:nn.MarginRankingLoss——排序损失
PyTorch学习笔记:nn.MarginRankingLoss——排序损失 torch.nn.MarginRankingLoss(margin0.0, size_averageNone, reduceNone, reductionmean)功能:创建一个排序损失函数,用于衡量输入x1x_1x1与x2x_2x2之间的排序损失(Ranking Loss)&…...

【JavaScript】34_Date对象 ,日期的格式化
8、Date Date 在JS中所有的和时间相关的数据都由Date对象来表示 对象的方法: getFullYear() 获取4位年份 getMonth() 返当前日期的月份(0-11) getDate() 返回当前是几日 getDay() 返回当前日期是周几(0-6) 0表示周日…...
计算机视觉 对比学习13篇经典论文、解读、代码
为了快速对 机器视觉中的对比学习有一个快速了解,或者后续复习,此处收录了 13篇经典论文、一些讲解地较好的博客和相应的Github代码,用不同颜色标记。 对比学习 13篇经典论文 论文代码和博客http://www.webhub123.com/#/home/detail?p…...

MySQL 选择数据库
在你连接到 MySQL 数据库后,可能有多个可以操作的数据库,所以你需要选择你要操作的数据库。 在 MySQL 中就有很多系统自带的数据库,那么在操作数据库之前就必须要确定是哪一个数据库。 在 MySQL 中,USE 语句用来完成一个数据库到…...

雅思经验(9)
写作:关于趋势的上升和下降在小作文中,真的是非常常见的,所以还是要积累一下。下面给出了很多词,但是在雅思写作中并不是词越丰富,分数就越高的。雅思写作强调的是准确性:在合适的地方用合适的词和句法。不…...
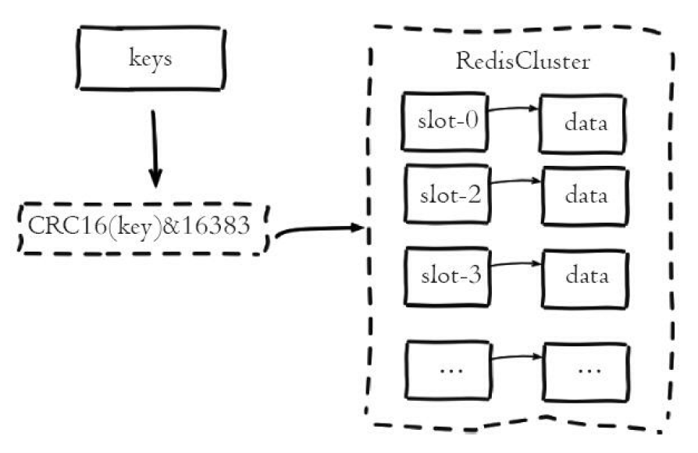
java面试题(二十)中间件redis
1.1 Redis可以用来做什么? 参考答案 Redis最常用来做缓存,是实现分布式缓存的首先中间件;Redis可以作为数据库,实现诸如点赞、关注、排行等对性能要求极高的互联网需求;Redis可以作为计算工具,能用很小的…...

JavaWEB必知必会-Servlet
目录 Servlet简介Servlet快速入门Servlet配置详解ServletContext 1 Servlet简介 Servlet 运行在服务端的Java小程序,是sun公司提供一套规范(接口),用来处理客户端请求、响应给浏览器的动态资源。但servlet的实质就是java代码&a…...
)
oralce查找返回不同的值,寻找不同的表(原创)
查找返回不同的值,寻找不同的表 select case a_id when 1 then (select b_id|| ||b_desc from b where b.b_ida.a_id) else (select e_id || ||e_desc from e where e.e_ida.a_id) end from a; 以上方法的缺陷是单表,判断。今天来了个挑战&#…...
Python-第四天 Python循环语句
Python-第四天 Python循环语句一、while循环1.while循环的基础语法2.while循环的基础案例3.while循环的嵌套应用4.while循环的嵌套案例二、for循环1.for循环的基础语法1.1基础语法1.2 range语句2.for循环的嵌套应用三、循环中断 : break和continue1.continue2.break四、 综合案…...
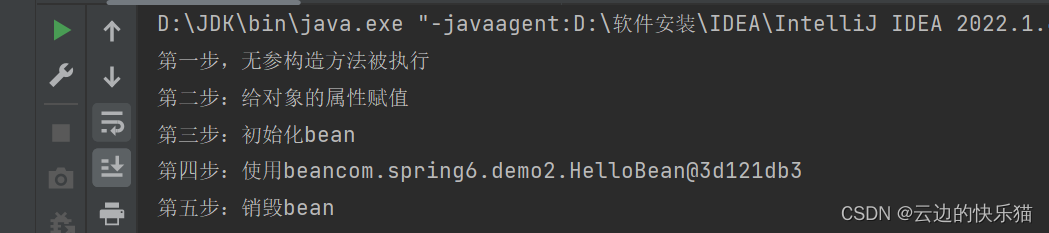
spring中bean的生命周期(简单5步)
目录 一、概念 1.生命是bean的生命周期? 2.知道bean生命周期的意义? 3.bean的生命周期按照粗略的五步 二、例子讲解 一、概念 1.生命是bean的生命周期? 答:spring其实就是管理bean对象的工厂,它负责对象的创建&…...

10 个最难理解的 Python 概念
文章目录技术提升面向对象编程 (OOP)装饰器生成器多线程异常处理正则表达式异步/等待函数式编程元编程网络编程大家好,与其他编程语言相比,Python 是一门相对简单的编程语言,如果你想真正学透这门语言,其实可能并不容易。 今天我…...
【linux】线程概念
概念 什么是线程 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列” 一切进程至少都有一个执行线程,线程在进程内部运行,本质是在进程地址空间内运行 在Linux系统中&a…...
Leg转Goh引擎和架设单机+配置登陆器教程
教程准备1、Leg版本一个2、Goh引擎一套3、电脑一台(最好联网)前言:BLUE/LEGS/Gob/Goh/九龍、4K、AspM2第一步:更换引擎1、把版本自带的LEG引擎换成Goh引擎2、删除服务端里面的exe、dll文件(也可以直接更新)3、清理登录和游戏网关里面的配置文件4、更新引…...

idea整合svn
idea整合svn svn下载 链接:https://pan.baidu.com/s/1yS3R3lEE8lm9c9Ap-ndDKg 提取码:65ur 基础步骤 IDED中配置SVN没有svn.exe解决办法 以下是两种解决方案 需要卸载原 svn(不推荐) 参考网址: https://blog.csdn.…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
