进阶理解:leetcode115.不同的子序列(细节深度)
这道题是困难题,本章是针对于动态规划解决,对于思路进行一个全面透彻的讲解,但是并不是对于基础讲解思路,而是渗透到递推式和dp填数的详解,如果有读者不清楚基本的解题思路,请看我的这篇文章算法训练营DAY53|392.判断子序列、115.不同的子序列-CSDN博客
但在看的过程中,你可能会有为什么把dp数组设为以i-1和j-1的下标这样的奇怪含义的困惑,这是为了方便初始化,不用对每一个位置进行一开始的判定初始化,也就是说可能要对于一开始下标匹配做一些多余的处理,详细的解释可以翻看我往期作品,其中会有更为详细的介绍,本期文章,我主要是针对,对于思路有一些了解,但是对于题解本身仍存有一些疑惑的读者准备的。
当然也是对于 我之前写的那期题解未能写的清楚的一些部分的补充。
这里还要纠正一下第一次写那个题解的一部分话是存在一些问题的,两个字符匹配的第一项并不是未匹配成功的结果,如果读者不能明白我在说什么直接看下面的代码即可,不必要去看那期文章,以避免误导读者。
class Solution {
public:int numDistinct(string s, string t) {int m=s.size(),n=t.size();vector<vector<uint64_t>>dp(m+1,vector<uint64_t>(n+1,0));for(int i=0;i<=m;++i)dp[i][0]=1;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];else dp[i][j]=dp[i-1][j];}}return dp[m][n];}
};如上是题目正确的代码,可以ac。
首先我们来分析的是递推式,然后是初始化和打表,最后是整体的总结。
先粘上一张代码随想录的图片,当大家需要看图对比时候可以回过头开看:
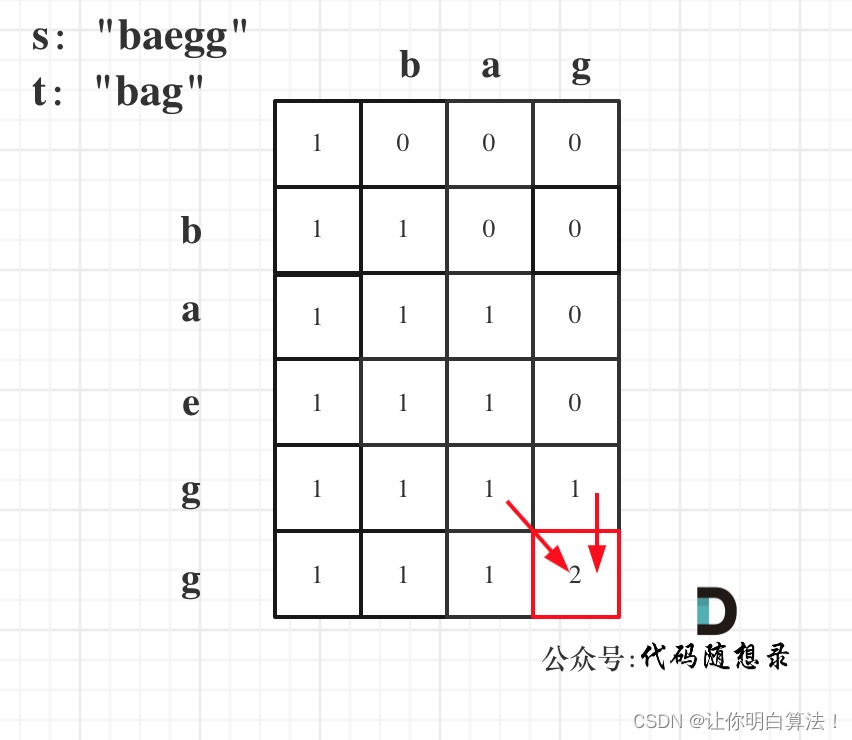
请注意:子序列问题中dp解决时,通常在需要在两个数组或字符串中找答案时候,大多数情况下都需要开辟二维dp数组来解决问题。
明确递推式dp【i】【j】代表以i-1和j-1结尾的字符串s和t,当前情况下,s字符串中t出现的个数有多少个。
递推公式:当i-1和j-1位置上的s和t字符串对应下标字符相等,则当前位置可由dp【i-1】【j-1】推出来,这个递推式的意思是由于这两个字符相等所以不用管该两个字符,
然后去看相当于i-2和j-2对应的位置下,s中包含了多少个t。
你也可以理解为当前的dp【i】【j】要填数,就要看上一个状态时,也就是dp【i-1】【j-1】的状态,因为此时对应下标的元素相等,所以直接去看上一个状态,而此时不需要删除元素
那上一个状态dp【i-1】【j-1】有没有可能需要删除元素呢?当然有可能,但这并不是我们本次填数需要解决的问题,上一个状态肯定在上一个状态被解决了。
为什么不是dp【i-1】【j-1】+1?当前字符相等应该意味着我们又多匹配成功了一个字符,所以理应+1啊
看这两个【bag】和【bag】当该填数dp【2】【2】时候,我们根据dp数组定义实际上看的是s的i-1下标,和t的j-1下标位置
那么也就是此时正在比较【ba】和【ba】呢,它的上一个状态是【b】【b】虽然匹配是相等,但是这并不意味着我们只要匹配相等字符就得+1
因为这道题求的不是重复字符最多有多少个!!!
那怎么完成匹配成功t字符串时候加入答案呢?因为有第二项递推式!
是dp【i-1】【j】这个递推式就相当于不回退当前的t字符串的匹配下标,而是回退s字符串下标,看看此时状态是否有s中有t字符串的这种情况
举例:【bagg】和【bag】这两个,那么除了s字符中的s[0]s[1]s[3]可以得到t字符串,s[0]s[1]s[2]这个组合也可以得到t字符串。
所以这正是我们可以回退s的原因,换个角度去看,这也是我们匹配t这个字符串的整个字符串的方法。把这两个递推式相加就可以得到dp【i】【j】了
我们不考虑t字符串回退的原因,在这里是因为我们是在s字符串里找有多少个t,而不是在t里找,所以应该回退s里的字符。如果你选择回退t此时对应的下标,那么将不可能得到正确答案,因为无论最后s能不能
从中找到t字符串的完整序列,只要t中的部分子数组在s中出现过,那么它一直沿用前面的状态,那是不是肯定会得到1次匹配?
你想想t一直沿用前面的状态,而最开始的状态是s有字符而t无字符,所以一定会有一解。这得出的答案一定是错误的。
所以t不可回退字符,t只能向前匹配,这样保证了求到最后的是s里是否包含完整的t字符串,而不是只要包含一部分子数组就可以完成匹配。
还有一件事是:s字符下标每次增大1然后重新对t字符串进行匹配,也就解决了以各个的s下标位置为截止,能匹配到最大匹配个数是多少。将它们加起来就是答案。
而如果此时两字符对应不等怎么办
dp【i】【j】=dp【i-1】【j】这里的递推式你可以理解为,删除s字符串当前遍历的字符(模拟删除)而转为用该下标的前一个位置看看有没有
s中含有t的时候,延续那时候的状态就可以了。
初始化也很重要它是得到答案的关键初始化dp数组,s和t数组都为空时候对应dp应该为1,解释:两字符串都为空,则s字符串里包含1个t
当s字符串有内容,t为空,那么s各个状态都为1,解释:s字符串删除全部字符得到空字符串也就是t
当s没内容,t有内容,则这些状态都为0,解释:s无论如何也无法推出t
当两字符串内容不相等时候,也就是s中不包含t那么无论如何也推不出一个,因为s里要想能找到t,那么必须t中的第一个元素与s中的某位置元素发生了起始匹配。
这时初始化产生作用,虽然这种中间某处得到的匹配,匹配不上原始的dp【0】【0】但是它能匹配上dp【i】【0】使得累计1次匹配。
然后接下来的匹配,就是对t字符串各个字符都必须连续匹配,才可以使这个1继承下来,因为递推式的缘故,往后匹配,dp【0】【0】肯定匹配不上
而如果中间某字符没匹配上断档了,那么再匹配上的时候,dp【i-1】【j】也不可能借用到dp【i】【0】就使得最终答案是0。
打表特殊测试用例 s=【bag】t=【bag】
dp[0][0]=1dp[0][1]=0dp[0][2]=0dp[0][3]=0
dp[1][0]=1dp[1][1]=1dp[1][2]=0dp[1][3]=0
dp[2][0]=1dp[2][1]=1dp[2][2]=1dp[2][3]=0
dp[3][0]=1dp[3][1]=1dp[3][2]=1dp[3][3]=1
可见即使中间遍历时候也有完全匹配时候【ba】【ba】但是这并不会使dp【2】【2】变成2
由头上的图片可以知道其实dp【i-1】【j-1】和dp【i-1】【j】都有可能是答案的组成部分
打表bac和bad
dp[0][0]=1dp[0][1]=0dp[0][2]=0dp[0][3]=0
dp[1][0]=1dp[1][1]=1dp[1][2]=0dp[1][3]=0
dp[2][0]=1dp[2][1]=1dp[2][2]=1dp[2][3]=0
dp[3][0]=1dp[3][1]=1dp[3][2]=1dp[3][3]=0
再写该题时候,写到循环部分的时候,想的是t字符串既然不能使之回退,那么是不是应该写成t循环在外面,s循环在里面,这样只循环了一次t,就保证了不回退的效果,而不是写成s循环在外面t循环在内部
但后来发现不是这么一回事,这样写循环是有原因的,它遍历s的各个字符给t去进行匹配,以获得所有的组合答案。如果t循环写外面了,t确实没有回退,但是这样写的思路不就成了拿t的各个元素去找
t里面是否存在s字符串了吗?这不就写反了吗?
还有就是外层for是s内层for是t,并不是没有实现t的禁止回退,所谓t字符串不能回退不是指t的字符串不能重复遍历,不能回退体现在递推公式上,不要弄混淆。
再细说一下具体的匹配机理,是如何实现s拿一个个字符串然后去匹配t的。
首先s字符串每次增大一个匹配范围(表面上看),然后t字符串在s每次增大匹配范围时,重新遍历t字符串去和s的现在范围去匹配,看看现在的s范围能否找到更多的匹配次数并填到dp数组内。
从代码的实际运行角度,s的每次增大一个字符的范围,t重新匹配,并不是匹配0——i,而是拿t的整个字符串去和i这个元素单单去匹配,而非s子串和t字符串匹配。
这实际上无形之中提升了效率,那么怎么实现匹配的正确呢?
递推式已经给出了,如果当前元素匹配不上,那么当前位置填数继承上一次匹配,也就是当前两个字符不匹配,那么相当于放弃当前两个字符的匹配机会,而是选用上一次的对应截止字符处,去继承那一次的
匹配成果。这次的继承是就是回退s而不回退t
如果匹配成功,有两个方向推出,一个是不考虑当前两个字符,因为两个字符当前匹配成功,所以暂时不考虑,但是还没完,还要考虑s往前回退一个字符的情况与t进行匹配的成果,将二者相加得到答案
为什么不回退第二个字符串t我们上面已经说得很清楚了,而回退s为上一个字符是为什么呢?就是因为bag和bagg的测试用例这类情况,也即是说可能存在上一个s的字符也存在匹配的关系,那有人要问
如果是bag和baggg呢?你怎么匹配?这是一样的,第二次的g会继承第一次g匹配成果,而第三次又会继承第二次.看递推式就能知道,两字符匹配成功,答案是左上角数加上头上的数,
而这个头上的数,自然把上一层的g加过来了。
还有一个问题是为什么总是能得到正确答案,我们上面已经说了一些了,但是个人觉得还不够透彻。再说一次
首先它为什么不是每匹配成功一次都+1我们上面说的很清了,当两个字符相等时候的填数再说一下
我们由于初始化的缘故,使得若此时匹配的两个字符匹配不相等,也就是说假如bagg和bag,s字符串bagg匹配到最后一个字符时候,但是t字符串从头开始匹配,这个时候我们由于第二递推式,匹配不等时候会拿
dp【i】【j-1】的数做继承,直到匹配成功填数的时候,真正的递推作用才开始显现
匹配相等时,会把头上的位置也就是dp【i-1】【j】和dp【i-1】【j-1】累加起来,换句话说只有两个字符最后发生匹配时候,才能够获得答案,如果不发生匹配不会获得答案。
这是为什么呢?不是说不匹配会继承前位置吗?但是你要注意,只有同列才能继承,也就是说如果你的上一行列没有做事,那么你不能享受成果,这就相当于祖上得有财富积累,你才能躺平拿到成果,否则你只能
依赖于本身的才能,也就是进入第一递推式,虽然祖上可能没有成果,但你可以收获你左上角人的成果。
所以并不会发生一处匹配成功,全部人都受益的结果。
你左上的成果相当于叔辈的成果,你没有能力时候它不会贡献成果给你享用,只有你的亲祖先才能共享成果,所以如果前面出现多次匹配,也就是说祖先和叔辈都得到了匹配,或他们继承它们的祖先和叔辈匹配
而且同时你也有能力匹配,才会同时得到两方面的匹配成果。
这个左上角匹配也并非与你完全无关,它有数字代表了发生连续匹配。
badgbacg打表
dp[0][0]=1dp[0][1]=0dp[0][2]=0dp[0][3]=0dp[0][4]=0
dp[1][0]=1dp[1][1]=1dp[1][2]=0dp[1][3]=0dp[1][4]=0
dp[2][0]=1dp[2][1]=1dp[2][2]=1dp[2][3]=0dp[2][4]=0
dp[3][0]=1dp[3][1]=1dp[3][2]=1dp[3][3]=0dp[3][4]=0
dp[4][0]=1dp[4][1]=1dp[4][2]=1dp[4][3]=0dp[4][4]=0
这下应该明白了吧,虽然祖上有成果的某些中间量会继承祖上的成果,但这并不一定影响最后的答案,该样例中即使最后一次发生了g和g的匹配,但是它的左上角没有成果也就是出现了断档,而且它的祖上也没有
成果,所以它依然无法收获结果。
这也就是说只要中间断档发生了一次,那么就不再可能延续的上,想尝试的读者可写一个badgh和bacgh试一下打表
简而言之:
对于当前两字符匹配成功,则需要收获结果,结果的第一部分代表了之前字符的连续匹配,第二部分代表了s中存在多个t的继承匹配个数
对于匹配不成功,继承连续匹配结果,这一举动主要是为了下一次的s扩大后的匹配受益,因为s当前字符不可能与t所有字符匹配,那么只要有一次完成了匹配,则这一列的所有位置理应继承那次匹配成功的成果。
以应对下一次循环匹配的时候,对于连续字符匹配的连贯性。
相信如果读者事先具备了代码思路,知道题解如何解答,再看这篇文章一定会受益匪浅。
这是对于细节上问题的一些补充。本章就到这里。
都看到这里了如果对您有用的话别忘了一键三连哦,如果是互粉回访我也会做的!
大家有什么想看的题解,或者想看的算法专栏、数据结构专栏,可以去看看往期的文章,有想看的新题目或者专栏也可以评论区写出来,讨论一番,本账号将持续更新。
期待您的关注
相关文章:

进阶理解:leetcode115.不同的子序列(细节深度)
这道题是困难题,本章是针对于动态规划解决,对于思路进行一个全面透彻的讲解,但是并不是对于基础讲解思路,而是渗透到递推式和dp填数的详解,如果有读者不清楚基本的解题思路,请看我的这篇文章算法训练营DAY5…...
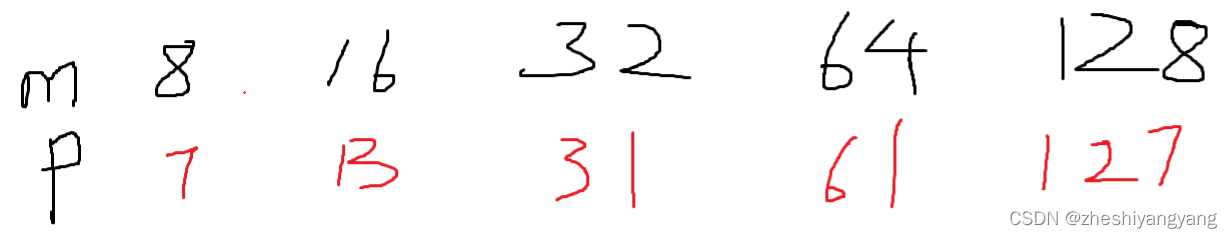
数据结构-哈希表(C语言)
哈希表的概念 哈希表就是: “将记录的存储位置与它的关键字之间建立一个对应关系,使每个关键字和一个唯一的存储位置对 应。” 哈希表又称:“散列法”、“杂凑法”、“关键字:地址法”。 哈希表思想 基本思想是在关键字和存…...
HCIA-综合实验(三)
综合实验(三) 1 实验拓扑2 IP 规划3 实验需求一、福州思博网络规划如下:二、上海思博网络规划如下:三、福州思博与上海思博网络互联四、网络优化 4 配置思路4.1 福州思博配置在 SW1、SW2、SW3 上配置交换网络SW1、SW2、SW3 运行 S…...

Java程序员的成长路径
熟悉JAVA语言基础语法。 学习JAVA基础知识,推荐阅读书单中的经典书籍。 理解并掌握面向对象的特性,比如继承,多态,覆盖,重载等含义,并正确运用。 熟悉SDK中常见类和API的使用,比如࿱…...

几种常用的排序
int[] arr new int[]{1, 2,8, 7, 5};这是提前准备好的数组 冒泡排序 public static void bubbleSort(int[] arr) {int len arr.length;for (int i 0; i < len - 1; i) {for (int j 0; j < len - i - 1; j) {if (arr[j] > arr[j1]) {int temp arr[j];arr[j] ar…...

性能测试【第三篇】Jmeter的使用
线程数:10 ,设置10个并发 Ramp-Up时间(秒):所有线程在多少时间内启动,如果设置5,那么每秒启动2个线程 循环次数:请求的重复次数,如果勾选"永远"将一直发送请求 持续时间时间:设置场景运行的时间 启动延迟:设置场景延迟启动时间 响应断言 响应断言模式匹配规则 包括…...

业务:业务系统检查项参考
名录明细云平台摸底1.原有云平台体系:VMware、openstack、ovirt、k8s、docker、混合云系列及版本 2.原有云平台规模,物理机数量、虚拟机数量、迁移业务系统所占配额 3.待补充系统摸底 (适用于物理主机)每一台虚拟机或物理机: 1.系统全局参数…...
解决公网下,k8s calico master节点无法访问node节点创建的pod
目的:解决pod部署成功后,只能在node节点访问,而master节点无法访问 原因:集群搭建时,没有配置公网进行kubectl操作,从而导致系统默认node节点,使用内网IP加入k8s集群!如下ÿ…...

六边形架构
Alistair Cockburn是于1953年出生在美国的一位软件开发方法学家。他毕业于康奈尔大学计算机科学专业,并获得了博士学位。 Cockburn在敏捷软件开发领域做出了许多重要的贡献,他被广泛认可为敏捷方法学的奠基人之一。他提出了许多关于敏捷开发的原则和实践…...

基于单片机的智能家居安保系统(论文+源码)
1.系统设计 本次基于单片机的智能家居安保系统设计,在功能上如下: 1)以51单片机为系统控制核心; 2)温度传感器、人体红外静释电、烟雾传感器来实现检测目的; 3)以GSM模块辅以按键来实现远/近程…...
盘点3种Python网络爬虫过程中的中文乱码的处理方法
网络爬虫过程中三种中文乱码的处理方案,希望对大家的学习有所帮助 一、思路 其实解决问题的关键点就是在于一点,就是将乱码的部分进行处理,而处理的方案主要可以从两个方面进行出发。其一是针对整体网页进行提前编码,其二是针对…...

小程序富文本图片大小问题
文章目录 概要uniapp小程序情况解决方法及完整示例 概要 在小程序使用富文本或者在nuiapp(小程序的)使用富文本都会转为 <rich-text nodes"<p class"p class">内容</p>”></rich-text>如果是这种情况的话在css…...
Diagrams——制作短小精悍的流程图
今天为大家分享的是一款轻量级的流程图绘制软件——Diagrams。 以特定的图形符号加上说明,表示算法的图,称为流程图或框图。流程图是流经一个系统的信息流、观点流或部件流的图形代表。我们常用流程图来说明某一过程。 流程图使用一些标准符号代表某些类…...
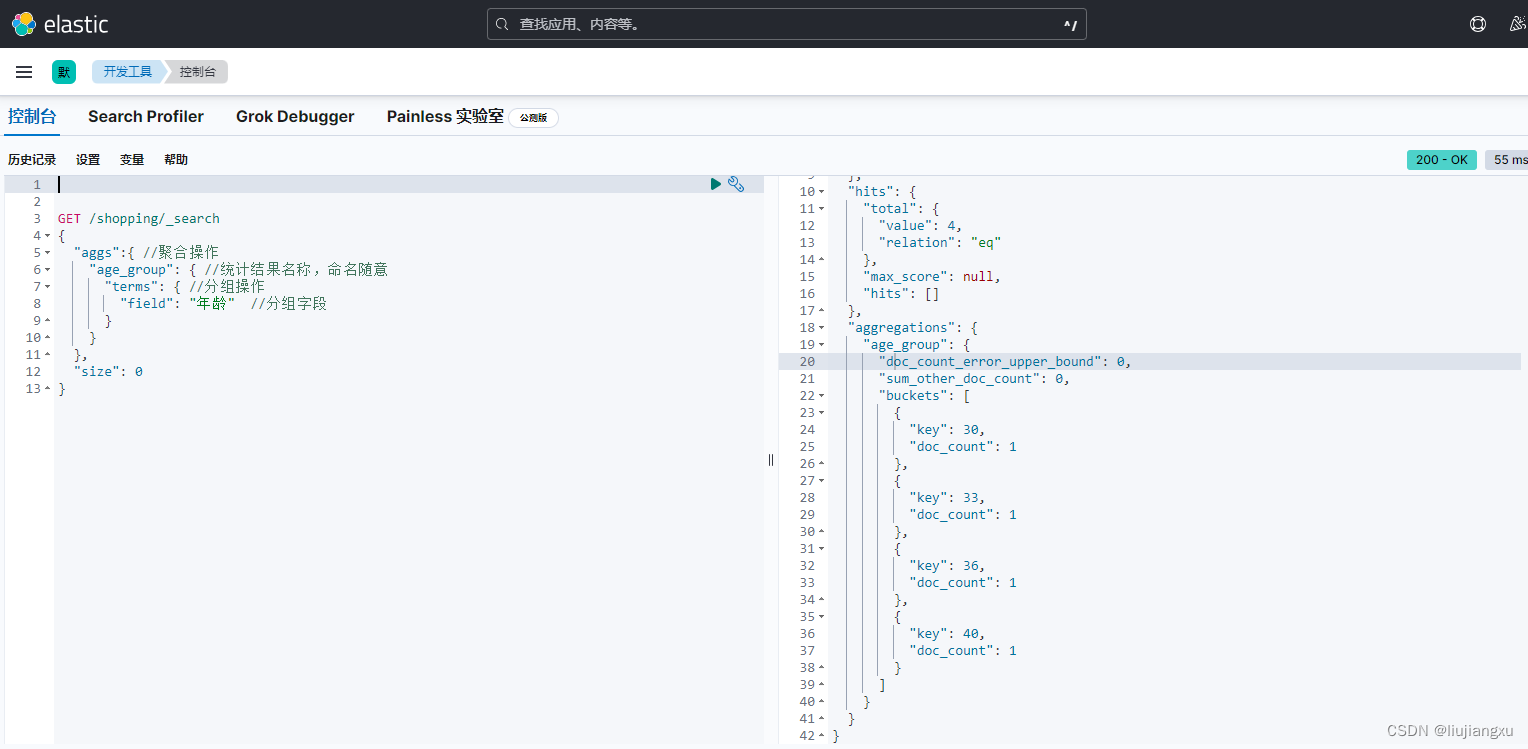
Elasticsearch基础条件查询
条件查询 query:查询 match:匹配 match_all:匹配所有 #第一种 GET /shopping/_search?q名字:张三#第二种 GET /shopping/_search {"query": {"match": {"名字": "张三"}} }#全量查询 match_all G…...

【SAP-ABAP】SAP与外围系统对接方式
SAP作为接受方 1.JAVA直接配置IP、账号、密码(有些人叫SAPWEBAPI)调用SAP里面的RFC函数 2.SAP发布RFC函数,配置webservice地址 3.SAP发布ODATA服务 4.SAP发布restful的http服务 5.我不太懂的UI5和FIORI本质好像也是odata服务 6.IDOC SA…...

云计算的发展趋势
云计算的发展一直是一个极具活力和创新的领域。随着技术的不断进步和应用场景的拓展,云计算将在未来继续发挥重要作用。以下是云计算发展的一些趋势: 边缘计算的崛起: 随着物联网设备的普及和应用场景的增多,边缘计算成为一个重要…...
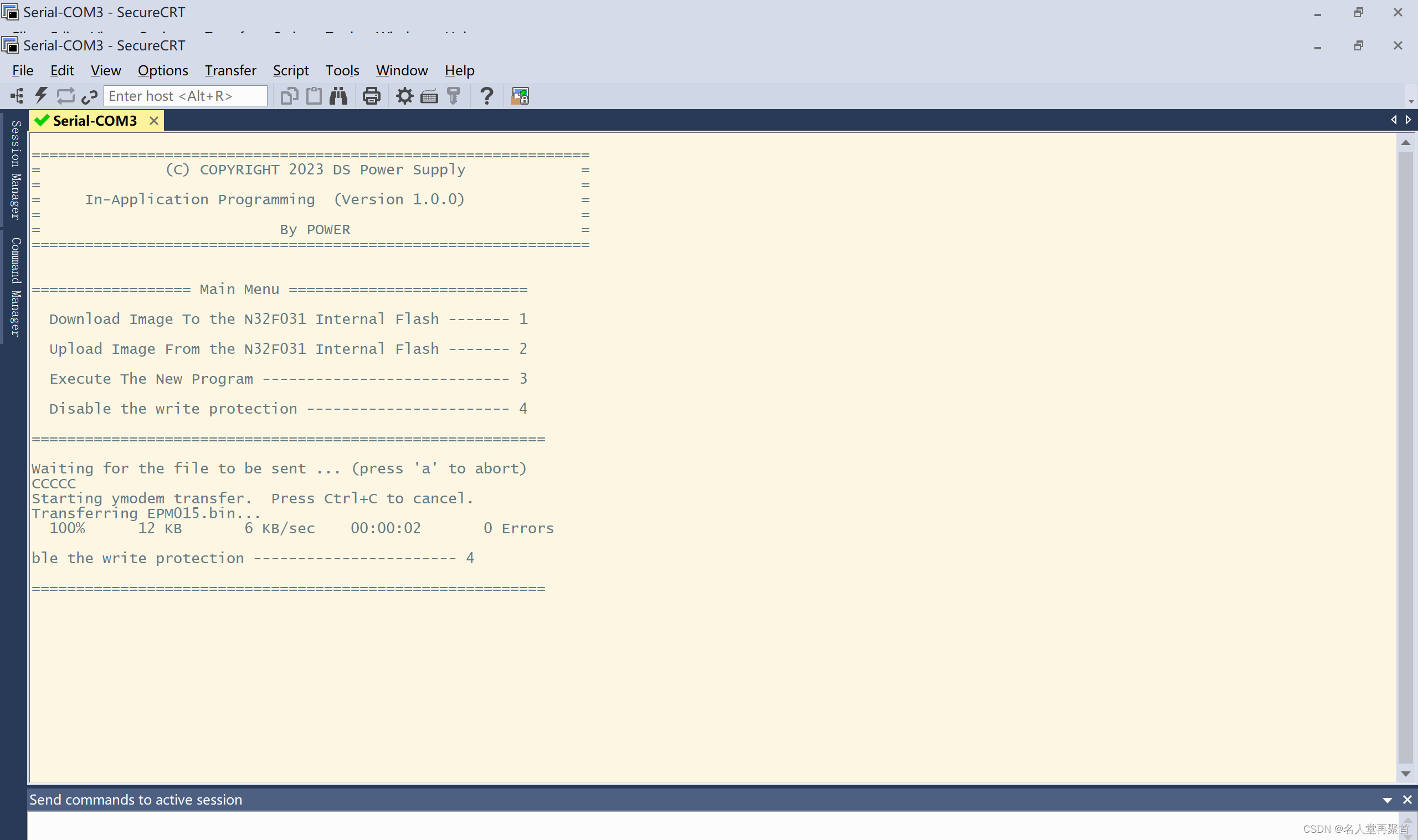
国民技术Cortex-M0系列单片机IAP升级
考虑到设备部署到现场后有可能需要进行软件升级,之前做过PIC系列单片机的升级,现在想做个国民技术N32G031系列Cortex-M0内核的单片机IAP方案。 因为国民技术系列单片机在很多大程度上都模仿了STM32,所以我想其升级方案极有可能差不多。于是在…...
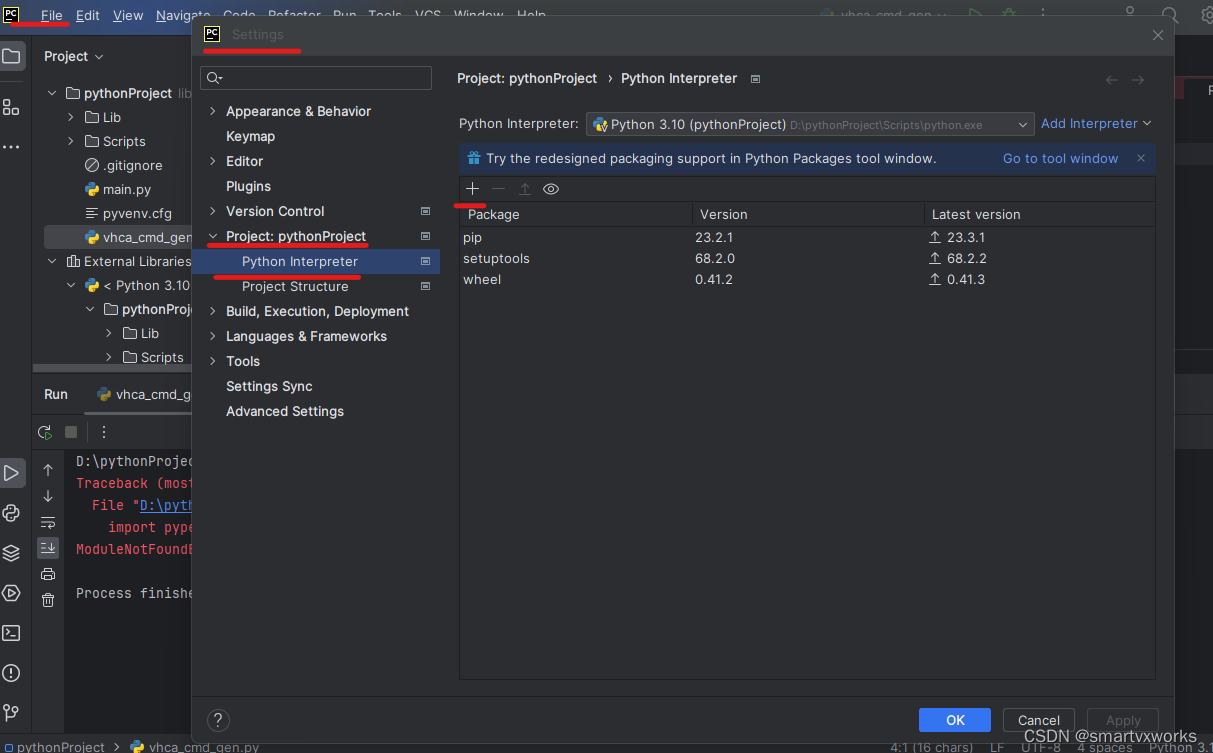
Pycharm中添加Python库指南
一、介绍 Pycharm是一款为Python开发者提供的集成开发环境(IDE),支持执行、调试Python代码,并提供了许多有用的工具和功能,其中之一就是在Pycharm中添加Python库。 添加Python库有许多好处,比如能够增加开…...

Oracle OCP / MySQL OCP认证容易通过吗
诸多学员在首次考OCP时,不清楚要如何选择。在本文中,我会为大家进行讲解! 选择OCP认证时需要考虑的几大项目: 授课老师师资经验 课程大纲 试听课程 考试通过率 业界口碑 服务质量 郭一军老师的OCP培训在业界培训的学员中已…...

flutter web 中嵌入一个html
介绍 flutter web 支持使用 HtmlElementView嵌入html import dart:html; import dart:ui as ui; import package:flutter/cupertino.dart;class WebWidget extends StatelessWidget {const WebWidget({super.key});overrideWidget build(BuildContext context) {DivElement fr…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
