NumPy:Python中的强大数学工具
NumPy:Python中的强大数学工具
文章目录
- NumPy:Python中的强大数学工具
- 一、NumPy简介
- 二、创建数组
- 三、数组尺寸
- 四、数组运算
- 五、数组切片
- 六、数组连接
- 七、数据存取
- 八、数组形态变换
- 九、数组排序与搜索
- 十、矩阵与线性代数运算
一、NumPy简介
当谈到数据科学和数值计算时,NumPy是Python编程语言中最重要的软件库之一。NumPy提供了强大的多维数组对象和一系列高效的函数和操作,以便在Python中进行数值计算和科学计算。
NumPy的核心是ndarray,即n-dimensional array,一种用于存储和处理多维数组的数据结构。NumPy中的数组可以包含不同类型的数据,包括整数、浮点数、布尔值和字符串等,这使得NumPy数组非常灵活。
NumPy的另一个关键功能是它提供了许多用于数组操作和计算的函数。例如,可以使用NumPy中的函数进行向量化操作,即对整个数组进行操作,而不是对数组中的每个元素进行单独的操作。这种向量化操作可以大大提高计算速度。
除了基本的数组操作和函数之外,NumPy还提供了许多其他的功能。例如,NumPy中有用于线性代数、随机数生成、傅里叶变换、信号处理和图像处理等领域的函数和类。此外,NumPy还可以与其他Python库和工具集(如Pandas和Matplotlib)集成使用,以便进行更复杂的数据分析和可视化。
总之,NumPy是Python编程语言中最重要的软件库之一,提供了强大的多维数组对象和一系列高效的函数和操作,使得Python成为一种优秀的数值计算和科学计算的工具。
二、创建数组
在NumPy中,有几种方法可以创建数组。以下是其中几种常见的方法:
-
使用numpy.array()函数创建数组:这是一种最基本的创建数组的方法,它接受一个序列(例如Python列表或元组)作为输入,并将其转换为NumPy数组。例如,下面的代码将Python列表转换为NumPy数组:
import numpy as npa = np.array([1, 2, 3, 4, 5]) print(a)[1 2 3 4 5] -
使用numpy.zeros()函数创建数组:这个函数创建一个由0组成的数组,并指定数组的形状。例如,下面的代码创建一个形状为(3, 4)的二维数组:
import numpy as npa = np.zeros((3, 4)) print(a)[[0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.]] -
使用numpy.ones()函数创建数组:这个函数创建一个由1组成的数组,并指定数组的形状。例如,下面的代码创建一个形状为(2, 3)的二维数组:
import numpy as npa = np.ones((2, 3)) print(a)[[1. 1. 1.][1. 1. 1.]] -
使用numpy.arange()函数创建数组:这个函数创建一个等差数列,并将其转换为NumPy数组。例如,下面的代码创建一个由1到9的整数组成的数组:
import numpy as npa = np.arange(1, 10) print(a)[1 2 3 4 5 6 7 8 9] -
使用numpy.linspace()函数创建数组:这个函数创建一个在指定范围内均匀分布的数组。例如,下面的代码创建一个由0到1之间的5个数字组成的数组:
import numpy as npa = np.linspace(0, 1, 5) print(a)[0. 0.25 0.5 0.75 1. ]
这些是一些在NumPy中创建数组的常用方法和示例。这些函数提供了许多选项,可以进一步自定义数组的形状、数据类型和其他特性。
三、数组尺寸
在NumPy中,可以使用shape属性获取数组的尺寸,它返回一个表示数组形状的元组,其中元组中的每个值表示该维度的大小。以下是一些示例:
import numpy as np# 创建一个二维数组
a = np.array([[1, 2, 3], [4, 5, 6]])# 获取数组的形状
print(a.shape) # 输出 (2, 3)# 创建一个三维数组
b = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])# 获取数组的形状
print(b.shape) # 输出 (2, 2, 2)# 创建一个一维数组
c = np.array([1, 2, 3, 4, 5])# 获取数组的形状
print(c.shape) # 输出 (5,)
在第一个示例中,我们创建了一个2x3的二维数组,并使用shape属性获取其形状,它返回一个元组(2, 3)。在第二个示例中,我们创建了一个2x2x2的三维数组,并使用shape属性获取其形状,它返回一个元组(2, 2, 2)。在第三个示例中,我们创建了一个包含5个元素的一维数组,并使用shape属性获取其形状,它返回一个元组(5,),这里使用的逗号表示这是一个元组,而不是单个整数。
除了shape属性之外,NumPy还提供了许多其他的属性和方法,用于获取和操作数组的尺寸和形状,例如ndim属性、size属性、reshape()方法等。这些方法可以帮助您更好地了解和操作数组的结构和形状。
四、数组运算
NumPy中的数组运算可以使用各种数学运算符和NumPy中提供的函数完成。以下是一些示例:
import numpy as np# 创建两个数组
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])# 加法
c = a + b
print(c) # 输出 [5 7 9]# 减法
d = a - b
print(d) # 输出 [-3 -3 -3]# 乘法
e = a * b
print(e) # 输出 [ 4 10 18]# 除法
f = a / b
print(f) # 输出 [0.25 0.4 0.5 ]# 按位求幂
g = a ** b
print(g) # 输出 [ 1 32 729]# 按位取余
h = a % b
print(h) # 输出 [1 2 3]# 求平方根
i = np.sqrt(a)
print(i) # 输出 [1. 1.41421356 1.73205081]
在上面的示例中,我们创建了两个NumPy数组a和b,然后使用加法、减法、乘法、除法、按位求幂、按位取余和求平方根等运算符对它们进行了各种运算。对于所有这些运算,NumPy会对数组的每个元素进行相应的运算。
此外,NumPy还提供了许多其他函数,用于对数组进行各种操作,例如sum()、mean()、std()、min()、max()等,这些函数可以对数组进行聚合操作,或者对数组中的元素进行排序、比较等操作。这些函数可以帮助您更好地了解和操作NumPy数组。
五、数组切片
在NumPy中,可以使用切片操作从数组中获取子数组或部分元素。切片操作使用[start:stop:step]的语法,其中start表示子数组的起始索引,stop表示子数组的结束索引(不包括该索引对应的元素),step表示切片步长。以下是一些示例:
import numpy as np# 创建一个一维数组
a = np.array([1, 2, 3, 4, 5])# 获取前三个元素
b = a[:3]
print(b) # 输出 [1 2 3]# 获取第二个到第四个元素
c = a[1:4]
print(c) # 输出 [2 3 4]# 获取每隔一个元素的子数组
d = a[::2]
print(d) # 输出 [1 3 5]# 反转数组
e = a[::-1]
print(e) # 输出 [5 4 3 2 1]# 创建一个二维数组
f = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 获取第一行
g = f[0, :]
print(g) # 输出 [1 2 3]# 获取第二列
h = f[:, 1]
print(h) # 输出 [2 5 8]# 获取前两行和前两列的子数组
i = f[:2, :2]
print(i) # 输出 [[1 2] [4 5]]
在上面的示例中,我们首先创建了一个一维数组a和一个二维数组f,然后使用切片操作从这些数组中获取子数组或部分元素。我们可以使用索引和切片操作来访问一维和多维数组的不同部分,这些操作可以让我们更方便地操作和处理数组中的数据。
六、数组连接
在NumPy中,可以使用各种函数将两个或多个数组连接在一起,以形成更大的数组。以下是一些示例:
import numpy as np# 创建两个一维数组
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])# 水平连接两个数组
c = np.hstack((a, b))
print(c) # 输出 [1 2 3 4 5 6]# 垂直连接两个数组
d = np.vstack((a, b))
print(d)
# 输出 [[1 2 3]
# [4 5 6]]# 深度连接两个数组
e = np.dstack((a, b))
print(e)
# 输出 [[[1 4]
# [2 5]
# [3 6]]]# 创建两个二维数组
f = np.array([[1, 2], [3, 4]])
g = np.array([[5, 6], [7, 8]])# 水平连接两个数组
h = np.hstack((f, g))
print(h)
# 输出 [[1 2 5 6]
# [3 4 7 8]]# 垂直连接两个数组
i = np.vstack((f, g))
print(i)
# 输出 [[1 2]
# [3 4]
# [5 6]
# [7 8]]# 深度连接两个数组
j = np.dstack((f, g))
print(j)
# 输出 [[[1 5]
# [2 6]]
# [[3 7]
# [4 8]]]
在上面的示例中,我们创建了一些数组,并使用hstack()、vstack()和dstack()函数将它们连接在一起。这些函数可以将两个或多个数组沿着不同的维度连接起来,例如在一维数组中进行水平连接,在二维数组中进行水平、垂直和深度连接。这些函数可以帮助我们更方便地将不同的数组组合在一起,并进行一些更复杂的操作和分析。
七、数据存取
NumPy提供了两个函数np.save()和np.load(),用于将数组存储到磁盘文件中以及从磁盘文件中加载数组。
np.save(file, arr, allow_pickle=True, fix_imports=True):将数组存储到磁盘文件中。file:文件名,字符串类型。arr:要保存的数组。allow_pickle:是否允许pickle序列化。默认为True。fix_imports:如果为True,则为Python 2和Python 3兼容性而导入pickle模块。默认为True。
np.load(file, mmap_mode=None, allow_pickle=True, fix_imports=True, encoding='ASCII'):从磁盘文件中加载数组。file:文件名,字符串类型。mmap_mode:如果给定,使用内存映射来加速读取大文件。默认为None。allow_pickle:是否允许pickle序列化。默认为True。fix_imports:如果为True,则为Python 2和Python 3兼容性而导入pickle模块。默认为True。encoding:如果数据文件是文本文件,则指定文件的编码格式。默认为’ASCII’。
以下是一个简单的示例,演示了如何使用np.save()和np.load()函数来保存和加载数组:
import numpy as np# 创建一个数组
arr = np.array([1, 2, 3, 4, 5])# 保存数组到文件
np.save('my_array.npy', arr)# 加载文件中的数组
loaded_array = np.load('my_array.npy')# 打印加载的数组
print(loaded_array)
在上面的示例中,我们首先创建一个数组arr,然后使用np.save()函数将它保存到文件my_array.npy中。接着,我们使用np.load()函数从文件中加载数组,并将其存储在loaded_array变量中。最后,我们打印loaded_array,以确认我们已经成功地加载了数组。注意,文件名包含文件扩展名.npy。保存和加载多维数组的方法与此类似,只是需要将数组作为参数传递给相应的函数。
八、数组形态变换
NumPy提供了一些方法,可以用于改变数组的形状或者大小。下面是几个常用的方法,并给出相应的示例:
-
reshape()方法:改变数组的形状,不改变元素个数import numpy as np# 创建一个3x4的数组 arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])# 将数组形状变为4x3 new_arr = arr.reshape(4, 3)print(new_arr)array([[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9],[10, 11, 12]]) -
resize()方法:改变数组的形状和大小import numpy as np# 创建一个3x4的数组 arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])# 改变数组的形状和大小为4x5 arr.resize(4, 5)print(arr)array([[ 1, 2, 3, 4, 5],[ 6, 7, 8, 9, 10],[11, 12, 0, 0, 0],[ 0, 0, 0, 0, 0]]) -
transpose()方法:交换数组的维度import numpy as np# 创建一个3x4的数组 arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])# 交换数组的维度 new_arr = arr.transpose()print(new_arr)array([[ 1, 5, 9],[ 2, 6, 10],[ 3, 7, 11],[ 4, 8, 12]]) -
flatten()方法:将数组展开为一维数组import numpy as np# 创建一个3x4的数组 arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])# 将数组展开为一维数组 new_arr = arr.flatten()print(new_arr)array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
这些方法可以方便地对数组进行形态变换,但需要注意的是,有些方法会直接修改原始数组的形状,而有些方法则会返回一个新的数组。在使用这些方法时,需要根据具体的需求来选择合适的方法来实现。
九、数组排序与搜索
NumPy提供了一些方法,可以对数组进行排序和搜索。下面是几个常用的方法,并给出相应的示例:
-
sort()方法:对数组进行排序import numpy as np# 创建一个随机数组 arr = np.array([3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5])# 对数组进行排序 arr.sort()print(arr)array([1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 9]) -
argsort()方法:返回数组排序后的索引值import numpy as np# 创建一个随机数组 arr = np.array([3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5])# 返回数组排序后的索引值 idx = arr.argsort()print(idx)array([ 1, 3, 6, 0, 9, 2, 4, 8, 10, 7, 5]) -
searchsorted()方法:返回要插入元素的索引值import numpy as np# 创建一个有序数组 arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])# 返回要插入元素的索引值 idx = np.searchsorted(arr, 5)print(idx)4 -
max()方法和min()方法:返回数组中的最大值和最小值import numpy as np# 创建一个随机数组 arr = np.array([3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5])# 返回数组中的最大值和最小值 max_value = arr.max() min_value = arr.min()print(max_value, min_value)9 1
这些方法可以方便地对数组进行排序和搜索,但需要注意的是,排序方法会直接修改原始数组,而搜索方法不会修改数组。在使用这些方法时,需要根据具体的需求来选择合适的方法。
十、矩阵与线性代数运算
NumPy提供了强大的矩阵和线性代数运算功能,下面介绍一些常用的运算方法,并举例说明:
-
创建矩阵
使用
numpy.array()函数可以创建矩阵。import numpy as np# 创建一个2x2的矩阵 matrix = np.array([[1, 2], [3, 4]])print(matrix)array([[1, 2],[3, 4]]) -
矩阵乘法
使用
numpy.dot()函数可以进行矩阵乘法运算。import numpy as np# 创建两个矩阵 matrix1 = np.array([[1, 2], [3, 4]]) matrix2 = np.array([[5, 6], [7, 8]])# 矩阵乘法 result = np.dot(matrix1, matrix2)print(result)array([[19, 22],[43, 50]]) -
矩阵的逆
使用
numpy.linalg.inv()函数可以求矩阵的逆。import numpy as np# 创建一个2x2的矩阵 matrix = np.array([[1, 2], [3, 4]])# 求矩阵的逆 inv_matrix = np.linalg.inv(matrix)print(inv_matrix)array([[-2. , 1. ],[ 1.5, -0.5]]) -
矩阵的转置
使用
numpy.transpose()函数可以求矩阵的转置。import numpy as np# 创建一个2x3的矩阵 matrix = np.array([[1, 2, 3], [4, 5, 6]])# 求矩阵的转置 transpose_matrix = np.transpose(matrix)print(transpose_matrix)array([[1, 4],[2, 5],[3, 6]]) -
矩阵的行列式
使用
numpy.linalg.det()函数可以求矩阵的行列式。import numpy as np# 创建一个2x2的矩阵 matrix = np.array([[1, 2], [3, 4]])# 求矩阵的行列式 det_matrix = np.linalg.det(matrix)print(det_matrix)-2.0 -
求特征值和特征向量
使用
numpy.linalg.eig()函数可以求解矩阵的特征值和特征向量。特征向量是在相应特征值下的非零向量。import numpy as np# 创建一个3x3的矩阵 matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 求解特征值和特征向量 eigenvalues, eigenvectors = np.linalg.eig(matrix)print("特征值:", eigenvalues) print("特征向量:", eigenvectors)特征值: [ 1.61168440e+01 -1.11684397e+00 -1.30367773e-15] 特征向量: [[-0.23197069 -0.78583024 0.40824829][ 0.52532209 -0.08675134 -0.81649658][-0.81867387 0.61232755 0.40824829]] -
奇异值分解
奇异值分解(Singular Value Decomposition,SVD)是一种用于矩阵分解的方法。它将矩阵分解成三个矩阵的乘积,即A=UΣVTA = U\Sigma V^TA=UΣVT,其中UUU和VVV是正交矩阵,Σ\SigmaΣ是一个对角矩阵,对角线上的元素称为奇异值。
使用
numpy.linalg.svd()函数可以进行奇异值分解。import numpy as np# 创建一个3x2的矩阵 matrix = np.array([[1, 2], [3, 4], [5, 6]])# 进行奇异值分解 U, S, VT = np.linalg.svd(matrix)print("U:", U) print("奇异值:", S) print("V转置:", VT)U: [[-0.2298477 -0.88346102 -0.40824829][-0.52474482 -0.24078249 0.81649658][-0.81964194 0.40189604 -0.40824829]] 奇异值: [9.52551809 0.51430058] V转置: [[-0.61962948 -0.78489445][ 0.78489445 -0.61962948]]
这些函数是NumPy中用于进行线性代数计算的一小部分。NumPy还提供了许多其他有用的线性代数函数,例如求解线性方程组、计算矩阵的行列式和求逆等。这些函数使得使用NumPy可以更加方便地进行线性代数计算。
相关文章:

NumPy:Python中的强大数学工具
NumPy:Python中的强大数学工具 文章目录NumPy:Python中的强大数学工具一、NumPy简介二、创建数组三、数组尺寸四、数组运算五、数组切片六、数组连接七、数据存取八、数组形态变换九、数组排序与搜索十、矩阵与线性代数运算一、NumPy简介 当谈到数据科学…...
Hbase资源隔离操作指南
1.检查集群的环境配置 1.1 HBase版本号确认> 5.11.0 引入rsgroup的Patch: [HBASE-6721] RegionServer Group based Assignment - ASF JIRA RegionServer Group based Assignment 社区支持版本:2.0.0 引入rsgroup的CDH版本 5.11.0 https://www.…...

TPS2012B泰克Tektronix隔离通道示波器
简 述: 复杂环境中开发和测试你的设计,进行浮动或差 分测量;100MHz,2通道 主要特点和优点 100 MHz和200 MHz带宽 高达2 GS/s的实时采样率 2条或4条全面隔离和浮动通道,外加隔离外部触 发 在安装两块电池时可以连续…...

9.4 PIM-DM
实验目的 熟悉PIM-DM的应用场景掌握PIM-DM的配置方法 实验拓扑 实验拓扑如图9-28所示: 图9-28:PIM-DM 实验步骤 (1)IP地址的配置 MCS1的配置如图9-29所示: 图9-29:配置MCS1的IP地址 R1的配置 <Huawe…...

程序员推荐的良心网站合集!
今天来给大家推荐几个程序员必看的国外良心网站合集。 IBM developer 技术性很强的博客网站,网站自带真实示例代码和架构解决方案,大家可以在上面找到适合自己的语言方向开始学习交流。 https://developer.ibm.com/ infoq 技术论坛社区,内…...

信息安全概论之《密码编码学与网络安全----原理与实践(第八版)》
前言:在信息安全概论课程的学习中,参考了《密码编码学与网络安全----原理与实践(第八版)》一书。以下内容为以课件为主要参考,课本内容与网络资源为辅助参考,学习该课程后作出的总结。 一、信息安全概述 1…...

跬智信息全新推出云原生数据底座玄武,助力国产化数据服务再次升级
2月28日,跬智信息(Kyligence)宣布全新推出国产化云原生数据底座开源项目玄武(XUANWU),以助力企业加速数据平台上云,并实现国产化升级。玄武(XUANWU)是在容器化技术上形成…...
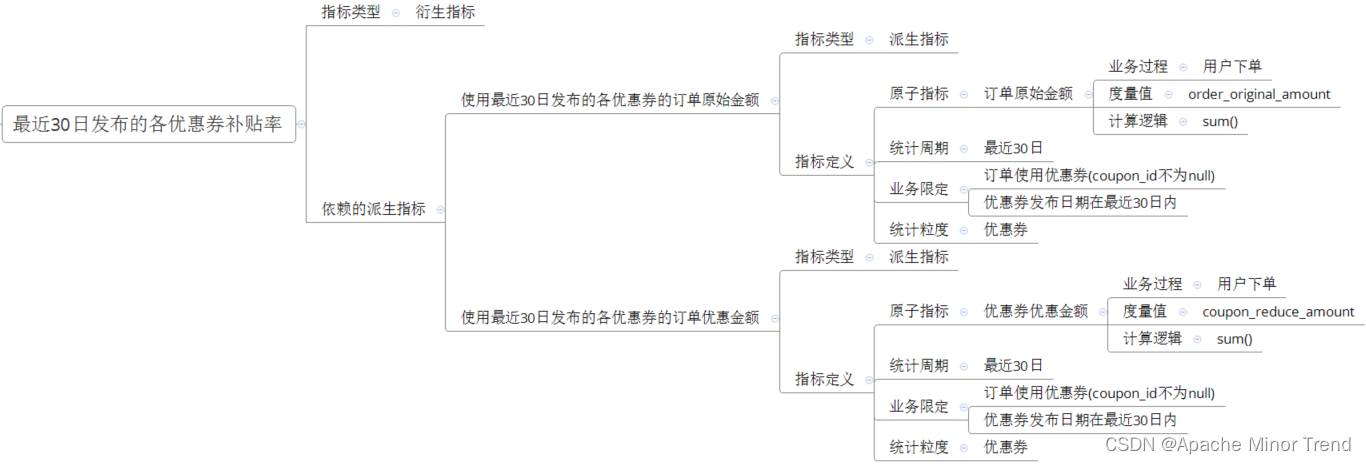
【离线数仓-9-数据仓库开发DWS层设计要点-DWS层汇总表以及数据装载】
离线数仓-9-数据仓库开发DWS层设计要点-DWS层汇总表以及数据装载离线数仓-9-数据仓库开发DWS层设计要点-DWS层汇总表以及数据装载一、交易域用户商品粒度订单最近1日/N日汇总表1.交易域用户商品粒度订单最近1日汇总表2.交易域用户商品粒度订单最近N日汇总表二、交易域优惠券粒度…...

我的十年编程路 序
算起来,从决定并从事编程开始,已十年有余了。 这十年是怎么算的呢? 我的本科是从2009年至2013年,现在回想起来,应该是从2012年下半年,也就是大四还未正式开始的时候决定从事Android开发。参加了培训班&am…...

xs 180
选择题(共180题,合计180.0分) 1. 你被任命为某项目的敏捷教练,为了更好的交付产品,你与团队召开会议,讨论项目过程中团队应该如何做到有效沟通。最有可能确定项目过程中主要以下列哪种方式沟通? A 团队成员在各自的办公室自行办公&#…...
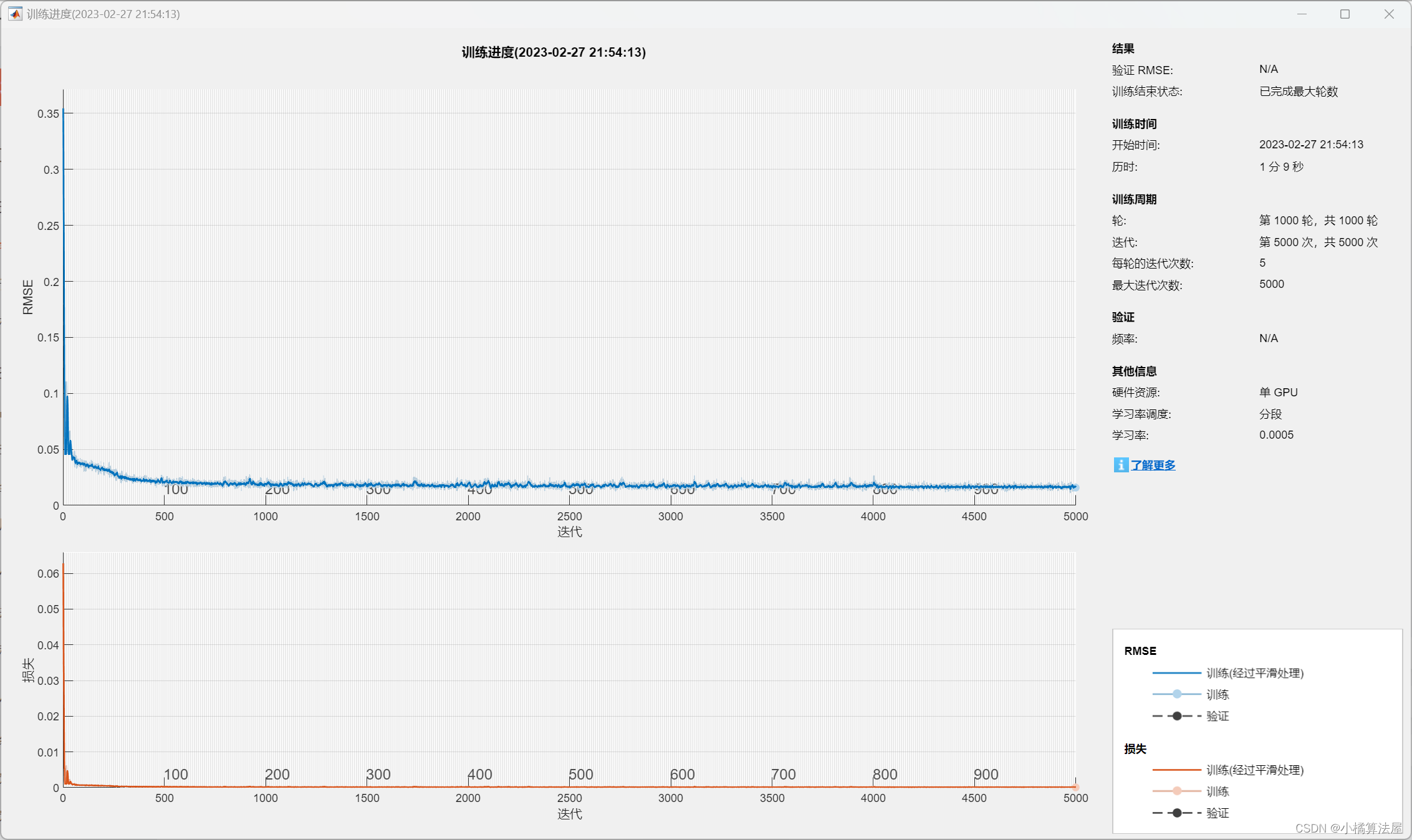
时间序列分析 | BiLSTM双向长短期记忆神经网络时间序列预测(Matlab完整程序)
时间序列分析 | BiLSTM双向长短期记忆神经网络时间序列预测(Matlab完整程序) 目录 时间序列分析 | BiLSTM双向长短期记忆神经网络时间序列预测(Matlab完整程序)预测结果评价指标基本介绍完整程序参考资料预测结果 评价指标 训练集数据的R2为:0.99302 测试集数据的R2为&…...

0101基础-认证授权-springsecurity
文章目录1 基础概念1.1 认证1.2 会话1.3 jwt1.4 授权2 授权的数据模型3 RBAC3.1 基于角色的访问控制3.2 基于资源的访问控制4 名词解析4.1 SSO4.2 CAS4.3 联合登陆4.4 多端登录:同一账号不同终端登录4.5 OAuth1 基础概念 1.1 认证 认证是为了保护系统的隐私数据和…...

一文简单了解THD布局要求
一、什么是THD? THD指总谐波失真。谐波失真是指输出信号比输入信号多出的谐波成分。谐波失真是系统不完全线性造成的。所有附加谐波电平之和称为总谐波失真。总谐波失真与频率有关。一般说来,1000Hz频率处的总谐波失真最小,因此不少产品均以…...
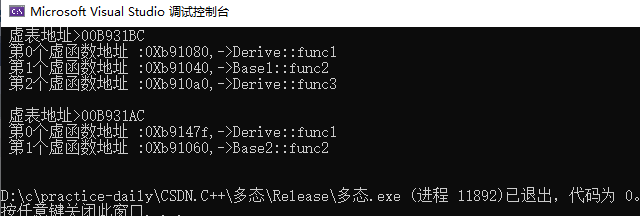
[C++]多态
🥁作者: 华丞臧 📕专栏:【C】 各位读者老爷如果觉得博主写的不错,请诸位多多支持(点赞收藏关注)。如果有错误的地方,欢迎在评论区指出。 推荐一款刷题网站 👉LeetCode 文章目录一、多态…...

中国版ChatGPT高潮即将到来,解密ChatGPT底层网络架构
2022年11月30日人工智能研究实验室OpenAI发布全新聊天机器人ChatGPT,在中国用户无法访问的前提下,上线仅两个月月活用户就突破了1亿。ChatGPT如同重磅炸弹,一时间火遍全球。面对这一万亿级市场机遇,在国内,无论是资本方…...

PingCAP 唐刘:一个咨询顾问对 TiDB Chat2Query Demo 提出的脑洞
导读 近日,TiDB Cloud 发布了 Chat2Query 功能,在 TiDB Cloud 上通过自然语言提问,即可生成相应的 SQL,通过 TiDB Cloud 对上传的任意数据集进行分析。Gartner 也在一份有关 ChatGPT 对数据分析影响研究的报告中提及了 PingCAP 的…...

力扣-销售分析III
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1084. 销售分析III二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结…...

U-Boot 之七 详解 Driver Model 架构、配置、命令、初始化流程
U-Boot 在 2014 年 4 月参考 Linux Kernel 的驱动模型设计并引入了自己的 Driver Model(官方简称 DM) 驱动架构。这个驱动模型(DM)为驱动的定义和访问接口提供了统一的方法,提高了驱动之间的兼容性以及访问的标准性。 …...

大数据算法重点
1 大数据亚线性空间算法 场景:用二进制存储一个数字N,需要log(N)的空间 问题:如果N特别大而且这样的N又特别的多,该怎么办呢? 思路:减少一些准确性,从而节省更多的空间。 解决办法:使…...

【Eclipse】The import xxxx cannot be resolved 问题解决
在Eclipse使用过程中,某一个类明明存在,但是使用import导入时,却总是提示The import xxxx cannot be resolved的错误,解决办法如下: 点击Project->Clean......

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
